带电粒子在圆形边界匀强磁场中的运动规律探究
2022-04-01刘东新
刘东新
(江苏省溧阳市光华高级中学 213300)
带电粒子在匀强磁场中做匀速圆周运动是比较常见的,匀强磁场分有边界和无边界,有边界的则又能分为直线边界、圆形边界等.由于边界的不确定导致看似简单的匀速圆周运动也变化多端.
1 作好“对称”图,解决单粒子问题
带电粒子以某一初速度进入圆形匀强磁场区域,再以同样大小的速度离开,具有对称性,入射方向与出射方向与径向的夹角相等,如图1.如果带电粒子沿径向入射,那么也一定沿径向射出,如图2.

图1 图2


图3 图4

2 巧作“旋转圆”,解决共源多粒子问题

题2 如图5所示,圆形区域有一匀强磁场,磁感应强度为B,方向垂直纸面向里,边界跟y轴相切于坐标原点O.O点处有一放射源,沿纸面向各方向射出速率均为v的某种带电粒子,带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍.已知该带电粒子的质量为m、电荷量为q,不考虑带电粒子的重力,求带电粒子通过磁场空间的最大偏转角.
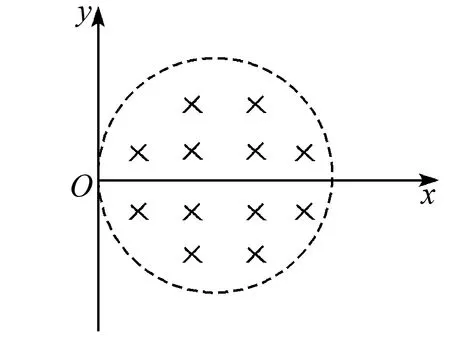
图5

图6 图7

如果带电粒子运动的轨迹圆半径小于磁场圆半径,又能产生新的问题.
题3如图8,虚线所示的圆形区域内存在一垂直于纸面的匀强磁场,磁感应强度为B,半径为r,P为磁场边界上的一点,大量相同的带电粒子以相同的速率经过P点,在纸面内沿不同方向射入磁场.若粒子射入速率为v,相应的出射点分布在三分之一圆周上.不计重力及带电粒子之间的相互作用,求带电粒子的比荷.

图8
简析如图9所示,通过旋转圆可知,当粒子在磁场边界的出射点A离P点最远时,则AP=2R,如图10所示.
由几何关系知:2R=2rcos30°

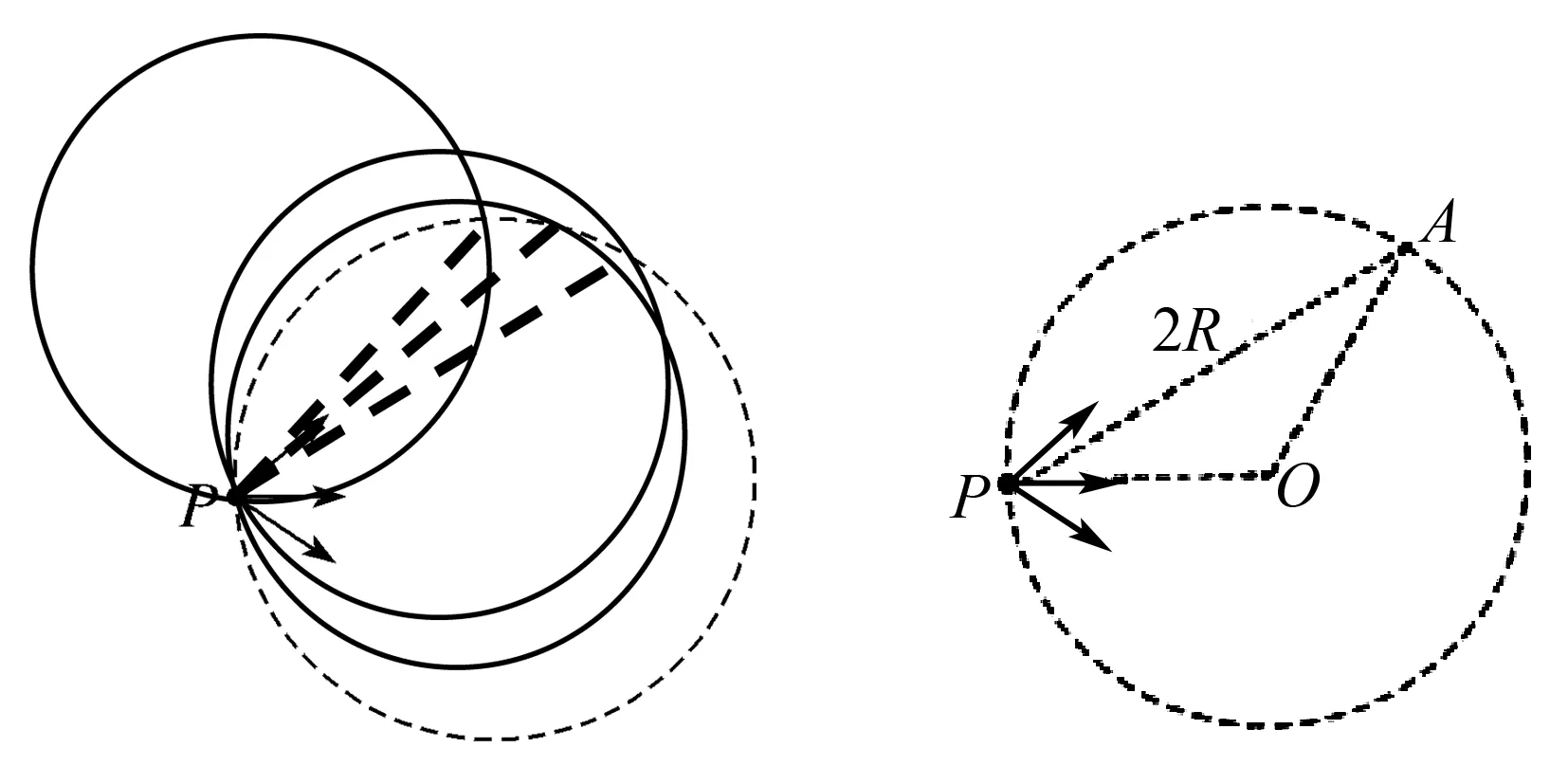
图9 图10
3 发散和汇聚,突破圆形边界匀强磁场的难点问题
在圆形边界的匀强磁场中,若带电粒子做匀速圆周运动的半径恰好等于磁场区域的半径,那么就有以下规律:当粒子从磁场边界上同一点沿不同方向进入磁场区域时,粒子离开磁场时的速度方向一定平行,而且与入射点的切线方向平行,此种情境称为“磁发散”,如图11甲所示.当粒子以相互平行的速度从磁场边界上任意位置进入磁场区域时,粒子一定会从同一点离开磁场区域,而且该点切线与入射方向平行,此种情境称为“磁汇聚”,如图11乙所示.

图11
题4 如图12所示, 在xoy平面内, 有一线状电子源沿x正方向发射速度均为v的电子,形成宽为2R、在y轴方向均匀分布且关于x轴对称的电子流.电子流沿+x方向射入一个半径为R、中心位于原点O的圆形匀强磁场区域, 磁场方向垂直xoy平面向里.在磁场区域的正下方d处,有一长为2d的金属板MN关于y轴对称放置,用于接收电子,电子质量为m,电量为e,不计电子重力及它们间的相互作用.

图12
(1)若正对0点射入的电子恰好从P点射出磁场,求磁感应强度大小B;
(2)若所有电子都能从P点射出磁场,MN板能接收到的电子数占发射电子总数的比例是多大?
简析MN板能接收到的电子从P点射出时,速度偏转角为θ(即与x正方向的夹角θ)满足45°≤θ≤135°.
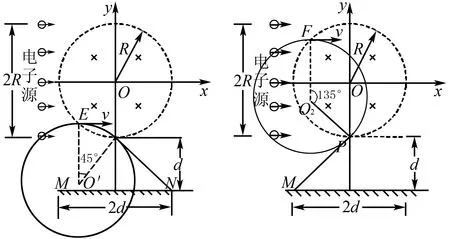
图13 图14

4 作好临界圆,解决圆环形磁场问题
当匀强磁场存在于一个圆环形区域时,带电粒子无论是从外部射入磁场,还是从内部射入磁场,与磁场边界相切的临界圆,往往就是解决问题的突破口.
带电粒子在圆形边界的匀强磁场中运动,其本质是匀速圆周运动,题目可能千变万化,但解决题目的的方法却是有限的.先确定粒子轨迹的圆心,进而作出粒子的运动轨迹,是解决这类问题的前提.在这个前提下,寻找题目的特征,弄清题目考查的内容,运用合适的方法,总能解决问题.
