适用于车联网的无证书强匿名聚合签名方案

高 岩,邓伦治,施虹宇,邵建鑫,胡震宇

(贵州师范大学 数学科学学院，贵州 贵阳 550025)

0 引言

车联网作为实现智能交通系统的必要技术手段，是解决当前交通问题的核心技术。车辆用户通过“车与车”和“车与基础设施”之间的通信共享信息来访问相邻的基础设施。然而，车联网因其自身的局限，如资源有限、高速移动的节点、通信延迟应该足够短等[1]。它的广泛应用存在着许多障碍。在车联网中，用户的信息泄露也会危及用户的生命和财产安全，因此构造安全的满足消息认证匿名性的方案尤为重要。

在传统的公钥基础设施(PKI)中，证书颁发机构(CA)需要将用户与他的公钥绑定[2]，这会造成证书管理和维护的成本。为了解决这个问题，Shamir[3]引入了基于身份的公钥密码体制。但是，私钥生成器(PKG)掌管用户的所有私钥，这对用户不安全。为了解决密钥托管问题，Al-Riyami等[4]引入了无证书公钥密码学(CL-PKC)，密钥生成中心(KGC)生成用户的部分私钥，另一部分由用户自己生成。

2003年，Boneh等[5]提出了聚合签名的定义，聚合签名是数字签名领域的一种“批量”和“压缩”技术，可以同时为多个消息和用户提供不可否认的签名服务。它可以将n个签名压缩为一个签名，这大大减少了签名的存储空间和网络的带宽需求。聚合签名可以将多个签名的验证简化为一个签名的验证，大大减少了签名验证的工作量。因此，聚合签名在很大程度上提高了签名验证和传输的效率。为了更好地应用于车联网，研究匿名的聚合签名方案有着重要的意义。

1 相关工作

Castro等[6]设计了第一个无证书聚合签名(CL-AS)方案，此方案的hash到点操作和签名的大小随着签名人的数量呈线性增加；Gong等[7]提出了两种基于双线性对的CL-AS方案，并在弱模型中给出了安全性证明；Zhang等[8-9]分别提出了一个新的CL-AS方案；在文献[6-7]的方案中，双线性对配对操作的数量随签名者的数量呈线性增加；因为文[6-9]的方案使用了大量的双线性对配对操作和hash到点操作，因此效率很低。Xiong等[10]提出了一个高效的CL-AS方案，只需要常数次的双线性对配对操作。He等[11]指出文[10]的方案存在安全漏洞，并提出了改进方案。但是，Li等[12]指出文[11]的方案仍然存在安全漏洞，一个恶意且被动的KGC可以伪造有效的签名。Liu等[13]和Chen等[14]分别提出了一个具有常数次双线性对配对运算的高效CL-AS方案；不幸的是，Zhang等[15]指出文[13-14]的方案对第I类和第II类敌手是脆弱的；2019年，Deng[16]设计了一种新的CL-AS方案，该方案只需要两次配对运算；2020年，Deng等[17]在标准模型下提出了一个新的CL-AS方案，该方案只需要3次配对运算。

以上所有的CL-AS方案[6-7, 10-17]都需要双线性配对运算。然而，双线性对配对运算比较耗时，不适合低功耗设备。因此，设计无双线性对配对运算的CL-AS方案是非常重要的。Tian[18]提出了一个无配对运算的CL-AS方案，但是他没有给出方案的安全性证明；2018年，Deng[19]提出了一个不需要双线性对配对运算的CL-AS方案，并给出了安全性证明；近年来，大量的用于车联网的CL-AS方案[20-24]被提出。Cui等[25]提出了一个高效的CL-AS方案用于车辆自组网(VANETs)，Kamil等[26]指出文[25]的方案无法抵抗第II类敌手的攻击，并构造了一个更高效的CL-AS方案用于VANETs。不幸的是，Ye等[27]和Zhao等[28]发现文[26]的方案无法抵抗伪造攻击。Ye等[27]和Zhao等[28]分别为车联网设计了新的CL-AS方案。但是Thumbur等[29]指出Zhao等[28]的方案是不正确的。

现有的适用于车联网的大多数CL-AS方案都没有考虑匿名性，少数考虑了匿名性的方案只能抵抗第I类敌手的攻击。如果敌手知道主密钥，就可以识别车辆用户的真实身份。因此，为车联网设计一个能够同时抵御两类敌手攻击的无证书强匿名聚合签名(CL-SAAS)方案显得尤为重要。本文结合CL-PKC和AS的优点，构造了一个具体的适用于车联网的CL-SAAS方案，以满足消息认证的匿名性、不可伪造性和可追踪性。与现存的一些CL-AS方案相比，我们的方案主要使用椭圆曲线上的标量乘法运算，没有使用双线性配对和hash到点运算，结果表明，我们的方案具有更高的效率。

本文给出了适用于车联网的CL-SAAS方案的系统模型和安全需求，在随机预言模型(ROM)下证明了我们方案的匿名性和不可伪造性。并且，我们的方案针对于超级敌手实现了强匿名。

2 预备知识

本节给出了椭圆曲线群(ECC)、离散对数(DL)问题和判定Diffie-Hellman(DDH)问题的定义。这些定义将用于我们的CL-SAAS方案。表1列出了本文中使用的符号。

表1 符号及其定义

假设E/Fp表示有限域Fp上的椭圆曲线E，满足方程：y=x3+ax+b(modp),a,b∈Fp和4a3+27b3≠0(modp)的所有解连同一个无穷远点O组成的集合构成一个群Γ={(x,y):x,y∈Fp,E(x,y)=0}∪{O}。

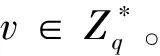
定义2 DDH问题:设G=

≤Γ是一个阶为q的加法循环群,给定一个元组(P,aP,bP,Z)，判断方程Z=abP是否成立。

3 适用于车联网的CL-SAAS方案的系统模型和安全定义

3.1 系统模型

适用于车联网的CL-SAAS方案由5个参与者组成：KGC、RTSA、Vehicle users(Vi)、Aggregate(Agg)和Verifier(Ver)，如图1所示。

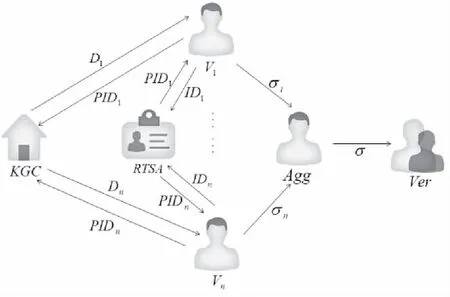
图1 适用于车联网的无证书聚合签名方案

KGC：负责生成系统参数和用户的部分私钥。

RTSA：一个可信任的第三方用来存储车辆用户的真实身份。

Vi：负责生成签名并将其发送给聚合者。

Agg：聚合者相当于车辆网中的网关，参与签名的聚合过程。聚合者也可以是签名的验证者。

Ver：负责判断此聚合签名是否为一个有效签名。

适用于车联网的CL-SAAS方案由以下9种算法组成：

设置：给定一个安全参数1λ，KGC输出系统参数params和主密钥msk。

伪身份生成：给定车辆用户身IDi∈{0,1}l，RTSA输出伪身份PIDi∈{0,1}l。

选择秘密值：车辆用户PIDi随机选择秘密值xi，计算Xi=xiP。

部分私钥提取:输入PIDi，KGC输出部分私钥Di。

公钥生成：车辆用户PIDi生成自己的公钥PKi。

签名：给定一个元组mi∈{0,1}*，车辆用户生成1个签名σi=(Ui,τi)。

验证：在收到元组(mi,σi=(Ui,τi))后，验证者判断σi=(Ui,τi)是否为有效的签名。

聚合：给定元组(mi,σi=(Ui,τi)),i=1,2，…，n,聚合者输出聚合签名σ。

聚合验证：在接收到元组(σ=(U1,U2,…,Un),mi,PKi,PIDi)后，如果σ为有效的签名，验证者输出1；否则，输出0。

3.2 安全定义

无证书密码体制中有两类敌手：类型I和类型II(A1和A2)。A1：知道秘密值xi，可以替换用户公钥PKi。A2：知道主秘钥s，但不能替换用户公钥。根据敌手类型的不同,分为如下3个游戏。

定义3 如果敌手在以下3个游戏中的优势可以忽略不计，那么CL-SAAS方案是不可伪造的。

游戏I 第一场比赛在挑战者C和第I类敌手A1之间进行。

初始化C运行设置算法生成msk和params。保持msk秘密，将参数发送给A1。

查询A1有权执行多项式查询。对于车辆用户IDi，敌手A1首先执行伪身份查询。

●H0-Query:A1可以向挑战者C查询任何的hash函数值。

●PID-Query:A1查询车辆用户IDi的伪身份，C返回相应的伪身份PIDi。

对于1个伪身份PIDi,A1首先执行PK-Query。

●PK-Query:A1为车辆用户PIDi查询公钥，C输出相应的公钥PKi。

●H-Query:A1可以向挑战者C查询任何的hash函数值。

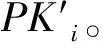
●PPK-Query:A1查询车辆用户PIDi的部分私钥，C返还相应的部分私钥Di。如果Ti已经被替换,A1将无法执行PPK-Query。

●SV-Query:A1查询车辆用户PIDi的秘密值，C返回秘密值xi给A1。如果Xi已经被替换，A1不能查询相应的秘密值。

●Sign-Query:A1提交元组(mi,PIDi,PKi)，C输出签名。

1)σi不是通过Sign-Query获得的。

2)验证(M°,σ°,A°)=1。

3)至少存在1个用户PIDi，A1没有对其执行PPK-Query或替换Tf。

A1的优势定义为：

游戏II 第二场比赛在挑战者C和第II类敌手A2之间进行。

初始化C运行设置算法生成msk和params。并将他们发送给A2。

查询A2执行与对游戏I相同的多项式查询。

1)σi不是通过Sign-Query获取的。

2)验证(M°,σ°,A°)=1。

3)至少存在1个用户PIDi,A2没有对其执行SV-Query或替换Xf。

A2的优势定义为：

在匿名性证明中，我们将不再区分敌手A1和A2，我们假定超级敌手A同时具有A1和A2的能力。

定义4 如果超级敌手A的优势在接下来的游戏中可以忽略，那么CL-SAAS方案是强匿名的。

游戏III 挑战者C和超级敌手A之间进行第三场游戏。

初始化和游戏II初始化阶段相同。

阶段1 执行和游戏I相同的多项式查询。

挑战A输入2个身份ID0和ID1，(其中A没有对ID0和ID1执行过伪身份查询)，C随机选择μ∈{0,1}，并输出伪身份PIDμ。

阶段2A执行与阶段1相同的查询，(但A不能对ID0和ID1执行伪身份查询)。

回应A返回u∈{0,1}，如果u=μ，敌手A赢得比赛。

解决DDHP。

A的优势定义为：

4 提出的新方案

4.1 方案描述

本节中，构建了1个新的CL-SAAS方案，该方案包括以下步骤：

设置：给定1个安全参数1λ，KGC通过执行如下算法输出参数params和秘密值msk={s}。

● 随机选取2个安全素数p和q，KGC生成椭圆曲线E:y=x3+ax+b(modp),a,b∈Fp，选择生成元P的加法群G，G由E上的点组成。

● 将params={p,q,a,b,P,Ppub,H0～H2}公布。

伪身份生成：在接收到身份为IDi∈{0,1}l的车辆用户后，RTSA执行如下操作：

● 计算RTSA的公钥PKRT=kP。

● 计算Pi=IDi⊕H0(kRi)。

● 发送伪身份PIDi=(Pi,Ri)给车辆用户。

部分私钥提取：对于车辆用户PIDi，KGC执行以下操作：

● 计算Ti=tiP，αi=H1(PIDi,Ppub,Ti,Xi)，Si=ti+αismodq。

● 输出Di=(Ti,Si)。

公钥生成：车辆用户PIDi通过公共网络公布他的公钥PKi=(Ti,Xi)。

签名：给定消息mi∈{0,1}*，车辆用户生成签名如下所示：

● 计算Ui=uiP，βi=H2(PIDi,Ppub,Ui,mi)，τi=βi(Si+xi)+ui。

● 输出签名σi=(Ui,τi)。

验证：接收到元组{mi,σi=(Ui,τi),PIDi,PKi}后，验证者执行以下步骤：

● 计算αi=H1(PIDi,Ppub,Ti,Xi)，βi=H2(PIDi,Ppub,Ui,mi)

● 检验等式τiP=βi(Ti+αiPpub+Xi)+Ui是否成立。

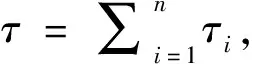
聚合验证：收到元组(σ,mi,PKi,PIDi),i=1,2,…，n

验证者执行如下操作：

● 计算αi=H1(PIDi,Ppub,Ti,Xi),βi=H2(PIDi,Ppub,Ui,mi)

4.2 方案安全性

本节中，我们的CL-SAAS方案在ROM中被证明是不可伪造的和匿名的。

定理1 在ROM中，如果DL问题难以解决，所提出的方案对第I类敌手A1是不可伪造的。

证明给定一个元组(P,vP)，C的目的是计算v，C在游戏I中扮演A1的挑战者。

初始C运行设置算法生成msk={s}和params={p,q,a,b,P,Ppub,H0～H2}。然后保持msk秘密并将参数params发送给A1。

查询A1可以执行一系列查询，C将创建几个空列表来存储查询和应答。对于车辆用户IDi,A1首先进行伪身份查询，然后再进行其他查询。

对于1个伪身份PIDi,A1将在任何其他查询之前首先执行PK-Query。

●PK-Query:A1输入1个身份PIDi,C执行如下操作：

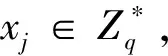
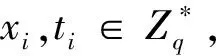
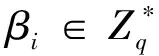
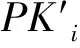
●PPK-Query:A1输入车辆用户的身份PIDi，如果PIDi=PID*，C失败。如果不等，C在表Lpk和L1中查找αi,ti，计算Si=ti+αis，输出Si。增加(PIDi,Si)到表Lppk。如果Ti被替换,A1将不再执行PK-Replace。

●SV-Query:A1输入车辆用户的身份PIDi,C查找xi在列表Lpk中，返回xi给Ai。如果Xi被替换，Ai将不再执行SV-Query。

●Sign-Query:Ai提交元组(mi,PIDi,PKi),C执行以下操作：如果PIDi≠PID*且PIDi不属于LR。C得到(xi,Si)通过调用Sign算法。如果PIDi=PID*或PIDi∈LR，C做如下操作：

2) 计算Ui=τiP-βi(Ti+αiPpub+Xi)

αi=H1(PIDi,Ppub,Ti,Xi)，

3) 设置H2(PIDi,Ppub,Ui,mi)=βi，

4) 添加(PIDi,mi,Ui,PKi,βi)到表L2，如果产生碰撞，重复执行1-4步骤，

5) 输出签名σi=(Ui,τi)。

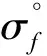
概率：让qHi(i=1,2),qPK,qPPK和qS分别表示Hi-Query，PK-Query，PPK-Query和Sign-Query的数量。定义3个事件：

π1：C在PPK-Query中没有失败

π2：C在Sign-Query中没有失败

π3：PIDf=PID*

成功解决DL问题的概率为：

Pr[Cwins]=Pr[π1∧π2∧π3]

=r[π1]·Pr[π2|π1]·Pr[π3|π1∧π2]

定理2 在ROM中，如果DL问题难以解决，所提出的方案对第II类敌手A2是不可伪造的。

证明给定1个元组(P,vP)，C计算v并在游戏II中扮演A2的挑战者。

初始化C运行设置算法生成msk={s}和params={p,q,a,b,P,Ppub,H0～H2}。然后将它们发送给A2。

查询A2可以执行一系列查询，C将创建几个空列表来存储查询和应答。对于车辆用户IDi,A2首先进行伪身份查询。

●H0-Query:和游戏I相同。

●PID-Query:和游戏I相同。

对于一个伪身份PIDi,A2将在其他查询之前首先执行PK-Query。

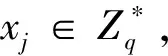
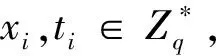
●Hi-Query：和游戏I相同。

●PK-Replace: 和游戏I相同。

●PPK-Query:A2输入车辆用户的身份PIDi，C查找(PIDi,xi,tiXi,Ti)在列表Lpk中，C输出Si通过调用部分私钥提取算法，增加(PIDi,Si)到表Lppk。

●SV-Query:A2输入车辆用户的身份PIDi，如果PIDi=PID*，C失败。如果不等，C在表Lpk中查找xi返还给A2。

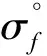
概率：让qH i(i=1,2),qPK,qSV和qS分别表示Hi-Query，PK-Query，SV-Query和Sign-Query的数量。定义3个事件：

π1：C在SV-Query中没有失败

π2：C在Sign-Query中没有失败

π3：PIDf=PID*

成功解决DL问题的概率为：

Pr[Cwins]=Pr[π1∧π2∧π3]

=Pr[π1]·Pr[π2|π1]·Pr[π3|π1∧π2]

定理3 在ROM中，如果DDH问题困难时，我们的方案对超级敌手是强匿名的。

证明给定1个元组(P,aP,bP,Z),C判断Z=abP是否成立。C是A的挑战者。

初始化和游戏II相同。设置PKRT=aP。

阶段1 执行和游戏I相同的多项式查询。

挑战A输入两个身份ID0和ID1，A没有对ID0和ID1执行过伪身份查询，C随机选择μ∈{0,1}，输出伪身份PIDμ。

阶段2A执行与阶段1相同的查询，但不能对ID0和ID1执行伪身份查询。

回应A返回u∈{0,1}，如果u=μ，敌手赢得比赛。

解决DDHP:

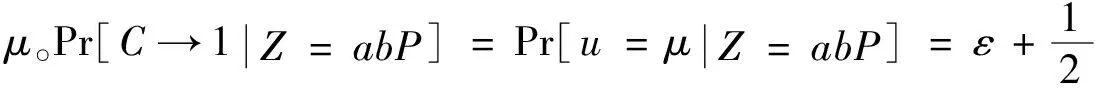
如果Z≠abP,PIDμ是一个无效的伪身份。因此，A没有ε的优势区分μ。

因此，C以ε的概率解决DDH问题。

5 效率比较

我们的方案在效率方面优于其他几个相关的CL-AS方案。我们分析了近五年6个CL-AS方案的效率，使用第三方数据计算了几个相关的CL-AS方案。根据Zhao等[28]运行在英特尔酷睿i7-7700 CPU@3.6GHz处理器和8GB内存的计算机上，实验采用vc++6.0中的基于配对的密码库得到了基本密码运算的运行时间(如表2所示)。为了实现1 024 RSA级别的安全性，我们使用了在椭圆曲线y=x3+ax+b(modp)上定义的阶是q的加法群G，p是512比特，q是160比特。

表2 基本密码运算的时间

接下来，我们用较为简便的算法来估算成本。Cui等[25]的方案需要2n+2次ECC中标量乘法运算，2n次ECC中加法运算和3n次hash运算。为方便起见，假设n=100，则计算时间为：0.032 1×202+0.001 8×200+0.008 5×300=9.394 2 ms;Kamil等[26]的方案需要5n次ECC中标量乘法运算，3n次ECC中加法运算和4n次hash运算，耗时为：0.032 1×500+0.001 8×300+0.008 5×400=20.44 ms；Zhao等[28]的方案需要3n+2次ECC中标量乘法运算，3n次ECC中加法运算和4n次hash运算，耗时为：0.032 1×302+0.001 8×300+0.008 5×400=13.634 2 ms；Ye等[27]的方案需要5n+1次ECC中标量乘法运算，4n-1次ECC中加法运算，3n次hash运算，耗时为：0.032 1×501+0.001 8×399+0.008 5×300=19.350 3 ms；Yang等[31]的方案需要7n+1次ECC中标量乘法运算，需要6n+3次ECC中加法运算和5n+1次hash运算，耗时为：0.032 1×701+0.001 8×597+0.008 5×501=27.835 2 ms；我们的方案需要4n+1次ECC中标量乘法运算，需要4n+1次ECC中加法运算和4n次hash运算，因此所消耗的时间为：0.032 1×401+0.001 8×399+0.008 5×400=16.990 3 ms。直观比较结果见图2。

图2 5个CLAS方案的通信成本

通过图2表可以看出，我们的方案具有效率优势。如相关工作的介绍，Cui等[25]的方案存在安全漏洞，因此在确保安全的前提下，我们的方案更高效，更适用于车联网。

6 总结

如何保证车联网中车辆节点之间安全传输的同时又保护车辆用户的身份信息不被泄露是一个重要的问题。本文提出了适用于车联网的CL-SAAS方案，它既满足了车辆用户对匿名性的需求，又实现了较高的计算和通信效率。在随机预言模型下，证明了该方案的不可伪造性和匿名性。通过性能比较看出，我们提出的CL-SAAS方案比现存的一些方案更具效率优势，更适合于车联网。