GKP方程和YTSF方程的行波解

韩青秀，刘红霞，伍 芸

(贵州师范大学 数学科学学院,贵州 贵阳 550025)

0 引言

随着非线性科学飞速发展，孤立子理论也越来越重要，(1+1)维、(2+1)维、(3+1)维的偏微分方程引起了许多数学家、物理学家的重视，例如，描述流体动力学和等离子体物理学中的许多非线性现象的(3+1)维GKP方程[1]；描述两层液体中晶格或界面波中的弹性准平面波的(2+1)维YTSF方程[2]等，它们的解可以解释许多物理、化学等科学中的现象。已有学者对其求解，例如Gao等[1]和Tian等[2]用Hirota双线性方法导出了一孤解、二孤解和N孤解，得到了GKP方程的一个块和一个扭结之间的交互解。Wang等[3]通过符号计算有更普遍的块解，研究了它在空间和时间的各个方向和更多的参数，通过块解得到了块波的移动路径，描述了一个条纹孤子和块波之间的相互作用，构造了YTSF方程的块化解。Cui[4]还应用一种简单的阿萨茨方法构造了变量分离解，求出GKP方程的一类块解;Chen等[5]通过符号计算，直接基于Hirota双线性公式生成块解和交互解，研究了(2+1)维YTSF方程的精确解，包括块解和相互作用解，又通过对相关参数的特殊选择，模拟和讨论了相互作用现象。因此，用不同的方法研究这两类方程可以得到不同形式的解，这些不同形式的解在实践中有重要意义，能够解释一些自然现象，在不同领域中选择恰当的解的形式可以快速解决问题。非线性方程与动力系统理论在物理数学、物理化学、自然科学现象等领域中具有非常广泛的应用背景，已经有了丰富的理论和广泛的应用，在这里主要是用动力系统定性理论[6-13]对GKP方程和YTSF方程进行研究。

1 GKP方程的精确行波解

考虑如下GKP方程[1]

uxxxy+3(uxuy)x+utx+uty-uzz=0

(1)

令u(x,y,z,t)=φ(ξ)，ξ=x+y+z-ct。其中c为波速且c>0。代入(1)式并积分，有

φ‴+3(φ′)2-(2c+1)φ′=g

(2)

其中g是积分常数。令φ′=v，则有

v″+3v2-(2c+1)v=g

(3)

令v′=y，则有

(4)

哈密顿系统(4)的哈密顿函数为

H(v,y)=y2+2v3-(2c+1)v2-2gv

(5)

令f(v)=-3v2+(2c+1)v+g，

Δ=(2c+1)2+12g。

则有

f′(v)=-6v+(2c+1)，

显然，若Δ>0，f(v)有2个零点va和vb，表达式为：

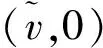
根据动力系统定性理论[12]，我们有如下结论：

(6)

(7)

(8)

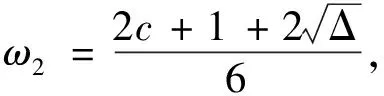
ω3ω4+ω3ω5+ω4ω5=-g,

C1、C3是积分常数。

图1 GKP的轨线图

将上式代入v′=y，则有

所以，积分上式可得

再由(3)式可以得到(1)式的孤立波解u1,见(6)式。

同理，对于图1(a)中的一条闭轨Γ2，令H(v,y)=H(vb,0)=hb，由(5)式可得

将上式代入v′=y，则有

完全积分上式

再由(3)式以及奇偶性可得到(1)式的周期波解u2,见(7)式。

将上式代入v′=y，则有

所以，积分上式

经验算，再由(3)式可得到(1)式的爆破波解u3,见(8)式。

2 YTSF方程的精确行波解

考虑如下YTSF方程[3]

-4uxt-uxxxx-6uxuxx+3uyy=0

(9)

令u(x,y,z,t)=φ(ξ),ξ=x+y+z-ct。其中c为波速且c>0。代入(9)式并积分，有

4cφ′-φ‴-3(φ′)2+3φ′=g

(10)

其中g为积分常数。令φ′=v，则有

v″+3v2-(4c+3)v=g

(11)

令v′=y，则有

(12)

哈密顿系统(12)的哈密顿函数为

H(v,y)=y2+2v3-(4c+3)v2-2gv

(13)

令f(v)=-3v2+(4c+3)v+g,

Δ=(4c+3)2+12g

则有

f′(v)=-6v+(4c+3),

显然，若Δ>0，f(v)有2个零点vd和vg，表达式为：

(14)

(15)

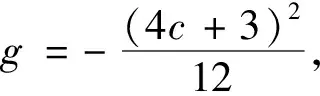
(16)

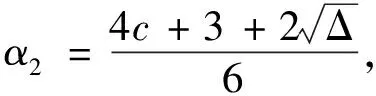
α3α4+α3α5+α4α5=-g,

C4和C6是积分常数。

图2 YTSF的轨线图

将上式代入v′=y，再积分可得

(17)

由(17)式可以得到(9)式的孤立波解u4,见(14)式。

同理，对于图2(a)中的一条闭轨Γ4的解，令H(v,y)=H(vg,0)=hg，可表示为

将上式代入v′=y，再积分有

(18)

由(18)式以及椭圆积分可得到方程(9)的周期波解u5,见(15)式。

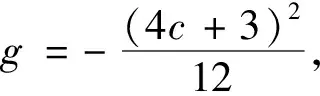
再积分，则有

(19)

由(19)式可得到方程(9)的爆破波解u6,见(16)式。

3 总结

这篇文章主要研究了GKP方程和YTSF方程的一些精确行波解，利用动力系统定性理论判断哈密顿系统有3种类型的奇点，分别是鞍点、中心和退化鞍点；通过Maple软件画出系统的相位图，利用椭圆积分公式，求解出孤立波、周期波以及爆破波的行波解，通过数值模拟，验证了这些解的正确性。