海量数据上有效的top-kSkyline查询算法*
2019-07-18韩希先戈韵如李建中
韩希先,宋 翠,戈韵如,高 宏,李建中
哈尔滨工业大学 计算机科学与技术学院,哈尔滨 150001
1 引言
在决策支持等多个应用中,Skyline查询是一种十分重要的查询类型,它在潜在的巨大的数据空间中返回用户感兴趣的数据[1-3]。给定属性集合作为Skyline准则,Skyline查询返回不被其他元组支配的所有元组。确切地说,元组t1支配元组t2,如果t1的所有Skyline准则中的属性值都不大于t2的对应属性值,并且在其中至少一个属性上,t1在该属性值小于t2在该属性值。Skyline查询的优点在于,它不需要特定的评分函数,并且不受维度之间不同标度的影响。
由于其实际应用的重要性,Skyline查询已经引起了研究人员的广泛关注。人们提出了一系列的算法来处理Skyline查询[1-8]。不同于top-k等返回固定数量结果的查询,Skyline查询返回的结果数量依赖于元组数量、Skyline准则的属性数量和数据分布[2]。分析发现Skyline查询的结果数量随着维度m的增大而指数级增长,尤其在海量数据上,即使m的值不是很大,查询结果数量也较多。在返回较多Skyline结果的情况下,用户很难在其中找到有用的信息。如何限制Skyline查询返回的结果数量,帮助用户快速地找到需要的数据就变成了一个很有趣的问题。
现有的具有大小限制的Skyline查询算法可以分为如下几类:基于点排序方法[9-12]、基于放松支配关系方法[13-15]和基于k-代表选择方法[16-20]。其中,基于放松支配关系方法放松了传统的支配定义,例如kdominant关系或ε-支配,从而可以丢弃更多的候选元组,减少了Skyline查询的结果数量。本文考虑的Skyline查询主要基于传统的支配定义。基于k-代表选择方法通过选择Skyline查询结果的满足指定原则的k子集,使得选择的k个Skyline点的整体度量最大化,例如支配最多的点,或者最大化偏好其中一个点的概率。基于k-代表选择问题基本都是NP-hard问题,只能提供近似的查询结果。本文主要考虑准确算法。基于点排序方法通过对Skyline点指定一个大小度量,例如Skyline frequency、Skyline点的兴趣度或者用户指定的偏好等,选择其中的度量值最大的k个结果。本文考虑基于点排序方法来计算top-kSkyline结果。
通过对现有工作的分析,发现现有的top-kSkyline算法忽略一个非常直观而且有效的基于传统支配关系的元组重要性的度量,即支配分数度量[21-23]。给定一个元组,该元组的支配分数定义为该元组支配的其他元组的数量。支配分数度量给元组定义了一个自然的顺序。支配分数越高,则表示该元组在数据空间中的位置越好,其重要性也越大。自然地,通过对Skyline的查询结果根据其支配分数的大小排序,top-kSkyline查询选择其中支配分数最大的k个Skyline元组。
本文考虑海量数据top-kSkyline查询。本文先提出一个baseline算法来解决top-kSkyline问题,即计算表T的Skyline结果,然后再执行一轮表扫描来计算Skyline元组的支配分数,返回支配分数最大的k个Skyline元组。在海量数据上,baseline算法需要维护较多的Skyline元组,从而在计算支配分数时带来较大的计算费用。同时,利用全表扫描来计算查询结果也导致较大的I/O费用。基于以上的分析,本文提出RSTS(ranked Skyline with table scan)算法来有效计算top-kSkyline结果,该算法不需要为特定的属性组合构建索引结构,只需要利用对预排序表的顺序扫描来有效返回查询结果。RSTS算法对数据表T执行预排序操作获得表PT(presorted table),按照对有序列表执行round-robin扫描的顺序排列PT的元组。RSTS算法的执行可以分为两个阶段。在阶段1,RSTS算法扫描表PT来获得查询结果的候选元组,当然,候选元组肯定是Skyline元组。在阶段2,RSTS算法同样采用对表PT的顺序扫描来计算候选元组的支配分数,并利用在扫描过程得到的信息继续剪切候选元组。本文分析证明,RSTS算法具有早结束特点,即该算法不需要扫描PT的所有元组就可以获得查询结果,还给出RSTS算法在阶段1和阶段2的扫描深度的理论分析。为减少阶段1需要维护的候选元组数量,本文提出有效的候选元组剪切规则,丢弃那些肯定不是查询结果的Skyline元组,理论剪切效果证明,剪切规则可以丢弃绝大多数候选Skyline元组。本文执行较广泛实验,实验结果表明,RSTS算法可以有效计算top-kSkyline查询。
本文的主要贡献如下所示:
(1)提出一个新的基于表扫描的RSTS算法来有效处理海量数据top-kSkyline查询;
(2)分析表明,RSTS算法具有早结束特点,并且提出其扫描深度的分析;
(3)提出剪切算法有效减少候选元组的数量;
(4)利用较全面实验评价RSTS算法性能。
2 相关工作
2.1 传统的Skyline算法
现有的Skyline算法可以分为两大类:基于索引的方法和一般性方法。基于索引的算法利用索引来减少需要探索的空间并返回结果。NN(nearest neighbor search)算法[4]利用预构建的R-树来计算Skyline结果。利用基于分支界定策略,BBS(branch and bound Skyline)算法[5]改进了NN算法同一节点的重复读取和空间负载高的问题。SUBSKY算法[6]利用一个特定的距离函数将多维数据转换为一维数据,并且以B-树索引来读取有序元组,可以较快地结束算法执行。
一般性方法不需要额外的数据结构,而是直接在数据表上执行。分治算法[1,7]将数据表划分为多个数据块,递归地计算每个块的部分Skyline结果,然后通过合并操作来获得数据表的Skyline结果。SFS(sort-filter-Skyline)算法[8]先根据与Skyline准则相符的顺序对数据表执行排序操作,再扫描排序表的元组维护候选Skyline结果,保证插入内存缓冲区的候选结果肯定是Skyline结果。LESS(linear elimination sort for Skyline)算法[2]整合排序操作和Skyline计算,从而减少SFS算法的排序费用,改进SFS算法的性能。
2.2 结果数量限制的Skyline算法
现有的结果数量限制的Skyline算法可以分为如下几类:点排序、放松支配关系和k-代表选择。
点排序:Chan等[9]提出一个新的度量Skyline frequency来对不同属性子集返回的Skyline点进行比较和排序,提出有效的近似算法来计算Skyline frequency最大的k个元组。Vlachou等[10]提出基于初始数据空间的所有非空子空间中的被支配Skyline点数量的Skyline点兴趣度的概念,Skyline点的所有子空间支配关系被映射成一个加权有向图Skyline graph,提出SKYRANK框架,基于链接的排序技术来对基于加权有向图的Skyline点进行比较和排序。Lee等[11]引入高维空间中的个性化top-kSkyline查询,提出基于用户指定的定性偏好关系的telescope算法对Skyline结果进行排序。Gao等[12]不但提出Skyline对象的一个新的排序准则,通过考虑一个Skyline点支配元组数量以及这些被支配的元组的累计权重来识别最重要的Skyline对象。而且提出基于R-tree的RB(reuse based algorithm)算法来计算最重要Skyline对象,首先通过现有基于R-tree算法来计算Skyline对象,然后通过在计算Skyline对象过程中缓存的中间结点和数据对象来计算Skyline对象的分数。
放松支配关系:Chan等[13]提出一个新的概念kdominant Skyline,将支配的定义放松到k-支配,给定具有属性维度M的表,如果存在k个属性(k≤M)作为Skyline准则,使得p支配q,称元组pk-支配另一个元组q。k-dominant Skyline查询返回所有没有被k-支配的元组。Koltun等[14]引入近似支配代表的概念来解决Skyline查询的较多输出结果问题。Xia等[15]提出ε-支配关系,放松传统的Skyline支配关系,方便地调整Skyline查询结果的数量。
k-代表选择:Lin 等[16]提出 top-krepresentative Skyline查询,该查询返回k个Skyline点,最大化数据表中被其中某个Skyline点支配的元组数量。Lee等[17]提出一个新的技术来选择可以最小化基于空间划分的Skyline计算中的比较操作数量的费用优化的点(pivot point),并提出基于由pivot point构建的skytree的贪心算法来计算top-krepresentative Skyline查询。Tao等[18]提出基于距离的representative Skyline查询,返回可以最好地描述所有Skyline点的可能的折衷的k个Skyline点,并最小化非代表Skyline点和其最近的代表Skyline点的最大距离。Sarma等[19]提出一个新的方法来定义representative Skyline,其目标是找到k个Skyline点,最大化一个随机用户偏好其中某个Skyline结果的概率。Magnani等[20]考虑代表性Skyline查询问题,并引入一个方法同时考虑所有元组的重要性及其多样性。
讨论:本文讨论基于传统支配关系的结果数量限制的Skyline算法。放松支配关系方法放松了传统的支配关系,而k-代表选择方法返回近似结果,并且k-代表选择方法返回的查询结果彼此之间本质上都是平等的,本文希望返回结果之间存在次序关系。因此,本文重点集中于点排序算法。本文提出的支配分数度量方法不同于其他点排序方法,大多数现有方法无法直接计算本文提出的问题。Gao等[12]提出的方法最接近于本文考虑的问题,但是RB算法需要在特定的属性组合上构建R-tree结构,要实际覆盖所有的属性组合就需要构建和所有属性数量成指数关系的R-tree,这是显然不实际的,RB算法的实际应用就受到较大限制。此外,该算法主要面向内存数据集,在处理海量数据时,该算法需要涉及较多的I/O费用。
3 预备知识
给定具有n个记录的表T(A1,A2…,AM),∀t∈T,令t.Ai表示元组t的属性Ai的值。不失一般性,令ASsky={A1,A2,…,Am}表示查询涉及到的Skyline准则,元组间的支配关系定义在ASsky。∀t1,t2∈T,称t1支配t2(表示为t1≻t2),如果∀i(1≤i≤m),t1.Ai≤t2.Ai,并且∃i(1≤i≤m),t1.Ai<t2.Ai。
∀t∈T,t的支配值dom(t)表示为T中被t支配的元组数量,即dom(t)=|{t'∈T|t≻t'}|。
定义1(Top-kSkyline查询)给定表T以及Skyline准则ASsky,令SKYT表示表T上的Skyline查询结果,top-kSkyline查询返回SKYT的一个k-子集R,使得∀t1∈R,∀t2∈(SKYT-R),dom(t1)≥dom(t2)。
根据支配分数定义,如果t1≻t2,dom(t1)≥dom(t2)。
定义2(位置索引)给定表T,如果t是T的第ath个元组,元组t∈T的位置索引是a。
用T(a)表示表T中位置索引为a的元组,用T(a,…,b)表示位置索引大于等于a且小于等于b的元组集合,用T(a,…,b).Ai表示T(a,…,b)中元组的属性Ai的集合。
4 Baseline算法
给定表T和Skyline准则ASsky,先提出直观的BA算法(baseline algorithm)来计算top-kSkyline查询的结果。BA算法的执行过程可以分为两步:Skyline计算和支配分数计算。其中,Skyline计算步骤可以采用现有的一般Skyline算法来计算表T的Skyline结果SKYT,由于其较好的实际性能,本文采用LESS算法来计算SKYT。接着,利用对表T的又一轮扫描操作,计算SKYT中每个Skyline元组的支配分数,返回其中支配分数最高的k个Skyline元组。
BA算法的执行比较简单。根据其实际的执行过程发现,LESS算法的主要费用来自于对表T的第一轮扫描,之后的排序操作和Skyline处理过程涉及到的数据量则要少得多。可以忽略后者的操作费用而不影响算法分析的结果。在支配分数计算过程中,BA算法仍然需要对表T执行一轮扫描,计算SKYT中每个Skyline元组的支配分数。因此,BA算法需要执行对表T的两轮扫描来返回查询结果,在海量数据上将引起较大的I/O费用。
针对BA算法的性能问题,本文提出RSTS算法来有效计算top-kSkyline结果。在候选元组计算过程中,通过对数据表的元组以一定顺序排列,RSTS算法可以只读取排序表的一部分元组就获得查询候选元组,并通过有效的候选元组剪切操作来减少候选元组的数量。此外,对于支配分数计算过程,RSTS算法同样利用排序表的有序性,从而只读取排序表的一部分元组就可以获得候选元组的支配分数。
5 预排序操作
本章介绍如何对数据表T执行预排序操作来获得预排序表PT。自从Fagin等的先驱性工作[24],利用有序列表来处理偏好查询已经成为研究人员自然的选择。在基于有序列表方法中,表T存储为有序列表集合LS={SL1,SL2,…,SLM},每个有序列表SLi的模式为SLi(PI,Ai),其中PI表示对应元组在表T的位置索引,Ai表示该元组在对应属性上的值,SLi根据Ai的值升序排列。
∀t∈T,令PIi(1≤i≤M)表示(t.PI,t.Ai)在有序列表SLi的位置索引,表PT的元组根据min1≤i≤MPIi的值升序排列,排序操作的实现方法描述如下。给定有序列表SLi(PI,Ai)(1≤i≤M),预排序操作首先对SLi(PI,Ai)执行排序操作,令排序后的有序列表表示为PSLi(PIi,PIT),这里PIT表示该元组在表T中的位置索引,PSLi(PIi,PIT)的元组根据PIT的值升序排列。由于本文算法只需要考虑每个属性的值的大小关系,因此PSLi不维护属性值Ai。很明显,PSL1,PSL2,…,PSLM中具有相同位置索引的元组对应于数据表T的具有相同位置索引的元组,∀j(1≤j≤n),令MPIL(j)表示PSL1,PSL2,…,PSLM的第j个元组的最小PIi值。接下来,预排序操作合并PSL1,PSL2,…,PSLM的元组并执行排序操作,使得其中的元组根据MPIL的值升序排列,排序后的数据表表示为PT(MPIL,PIT,PI1,PI2,…,PIM)。令当前读取的元组pt∈PT,文献[25]证明,当前已读取的PT元组肯定包括SL1(1,2,…,pt.MPIL-1),SL2(1,2,…,pt.MPIL-1),…,SLm(1,2,…,pt.MPIL-1)的所有元组。根据有序列表的有序性,∀pt1,pt2∈PT,如果∀1≤i≤m,pt1.PIi<pt2.PIi,称pt1≻pt2,即T(pt1.PIT)≻T(pt2.PIT)。
6 RSTS算法
RSTS算法的基本执行过程包括两个阶段:在阶段1中,算法顺序扫描表PT的元组,维护top-kSkyline查询的候选元组;在阶段2中,算法计算当前的候选元组的支配分数,返回查询结果。
6.1 阶段1:维护候选元组
在表扫描过程中,用STCAD维护当前的候选元组。令当前读取的元组pt=PT(j)。如果∃cad∈STCAD,cad≻pt,那么pt肯定不是Skyline元组,自然也不是top-kSkyline元组。否则,RSTS算法在STCAD中维护pt,并且丢弃那些在STCAD中被pt支配的候选元组。令 max1≤i≤mpt.PIi表示pt.PI1,pt.PI2,…,pt.PIm中的最大值,sd1表示已读取元组的PI1,PI2,…,PIm属性最大值的当前最小值,即。
定理1表明,当结束条件sd1≤pt.MPIL满足时,阶段1结束,top-kSkyline查询结果包括在STCAD中。
定理1令当前读取的元组pt=PT(j),当sd1≤pt.MPIL时,阶段1结束并且top-kSkyline查询结果包括在STCAD中。
证明∀t∈T,PIi(1≤i≤M)表示(t.PI,t.Ai)在有序列表SLi中的位置索引。∃j1(1≤j1≤j),sd1=max1≤i≤mPT(j1).PIi。已知,pt.MPIL表示pt.PI1,pt.PI2,…,pt.PIM的最小值,有序列表SL1,SL2,…,SLm是根据属性值Ai升序排列,如果sd1≤pt.MPIL,有PT(j1)≻pt。再考虑到PT的元组根据MPIL的值升序排列,那么 ∀pt′∈PT(j,…,n),PT(j1)≻pt′,表PT剩余的元组肯定不是Skyline结果。根据阶段1的执行过程,STCAD维护的就是Skyline结果,肯定包括top-kSkyline结果。 □
虽然可以维护所有的Skyline元组,但是在海量数据上,通常k≪|SKYT|,没有必要维护所有的Skyline元组。第一,大多数的Skyline元组不是top-kSkyline结果;第二,在计算候选元组的支配分数时,较多的候选元组也会造成较大的计算费用。下面介绍如何减少需要在STCAD维护的候选元组数量。
给定Skyline准则ASSKY,∀pt∈PT,该元组的支配分数的下界值LDS和上界值UDS分别计算如下:
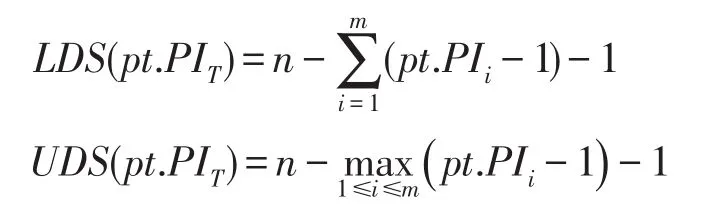
在对表PT的扫描过程中,令STSKY⊆STCAD,并且∀pt∈STSKY,pt.MPIL=pt.PIi(∃i,1≤i≤m),定理2证明,STSKY中维护的元组肯定是Skyline元组。
定理2令STSKY⊆STCAD,并且满足∀pt∈STSKY,pt.MPIL=pt.PIi(∃i,1≤i≤m),STSKY中维护的元组肯定是Skyline元组。
证明给定当前读取的元组pt∈PT,并且满足pt.MPIL=pt.PIi(∃i,1≤i≤m),如果STCAD中不存在支配pt的元组,那么RSTS算法将pt插入到STCAD。∀pt1∈PT,如果pt1.PIi<pt.PIi,那么根据PT元组的有序性,pt1肯定在pt的前面出现,而已经假设pt没有被之前出现的元组支配。对于在pt之后出现的元组pt2,有pt.PIi<pt2.PIi,即在pt之后出现的元组不能支配pt。因此,STSKY中维护的元组肯定是Skyline元组。 □
RSTS算法计算当前STCAD中候选元组的支配分数的上界值和下界值,并利用最小堆MH来维护STSKY中支配分数的下界值最大的k个候选元组,令MH.min表示MH中的最小的支配分数下界值。提出如下剪切规则减少在STCAD中需要维护的候选元组数量。
令pt是当前读取的表PT元组,且pt没有被STCAD的候选元组支配,如果UDS(pt.PIT)≤MH.min,那么pt不是候选元组。
根据剪切规则,如果pt没有被STCAD的候选元组支配,RSTS算法计算pt的支配分数下界值LDS(pt.PIT)和上界值UDS(pt.PIT),如果UDS(pt.PIT)≤MH.min,那么pt肯定不是top-kSkyline结果,从而RSTS算法不需要在STCAD中维护pt。否则,RSTS算法在STCAD中维护pt。同时,如果LDS(pt.PIT)≥MH.min,RSTS算法更新MH,保证其维护STSKY中支配分数的下界值最大的k个候选元组。
先分析阶段1的扫描深度,给定sd1表示已读取元组的PI1,PI2,…,PIm属性最大值的当前最小值。已知pt.MPIL表示pt.PI1,pt.PI2,…,pt.PIM的最小值,RSTS算法最多扫描M×sd1个PT元组就可以使得当前元组满足阶段1结束条件pt.MPIL≥sd1。下面分析sd1的值。由定义可知,∃j1(1≤j1≤j),sd1=max1≤i≤MPT(j1).PIi即PT(j1).PI1≤sd1,PT(j1).PI2≤sd1,…,PT(j1).PIm≤sd1。
假设1属性A1,A2,…,AM的值均匀独立分布。
下面分析剪切规则1的剪切效果。
先估计MH.min的值。如图1所示,给定Skyline准则ASsky和1≤sdk≤n,m维空间的坐标 (sdk,…,sdk)将空间划分为2m个子空间SSb1b2...bm,∀i(1≤i≤m),如果SSb1b2...bm[i]=[1,sdk],bi=0;如果SSb1b2...bm[i]=[sdk,n],bi=1。其中,SSb1b2...bm[i]表示子空间SSb1b2...bm在第i维上的投影区间。SKY(SS0…0)肯定是Skyline结果。基于假设1,子空间SS0…0包括元组数量n0=n×(sdk/n)m,SKY(SS0…0)的结果数量,令。因此,。
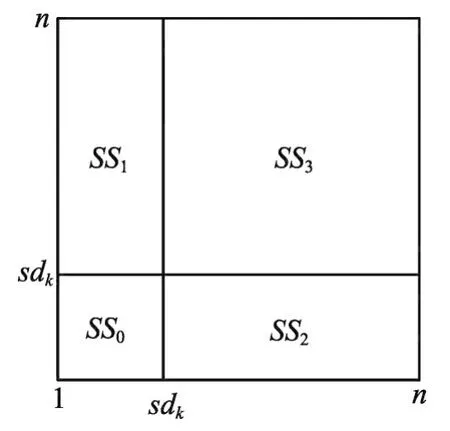
Fig.1 Illustration of region partitioning for Skyline computation图1 区域划分Skyline计算图示
如果 max1≤i≤mpt.PIi≥m×sdk-m+1,根据剪切规则,候选元组pt肯定可以被剪切。下面来分析剪切规则的理论剪切效果。如图2所示,给定m×sdkm+1,可以将空间划分为2m个子空间USb1b2...bm,∀i(1≤i≤m),如 果USb1b2...bm[i]=[1,m×sdk-m+1],bi=0,如 果USb1b2...bm[i]=[m×sdk-m+1,n],bi=1。根据剪切规则,除US0…0外,落入其他子区间的Skyline结果可以被剪切。例如,如图2所示,落入US01和US10的Skyline元组可以被剪切规则剪切。基于假设1,子空间US0…0包括的元组数量的结果数量。给定Skyline结果数量,剪切规则的剪切比例。根据pp的计算公式,剪切规则1将丢弃大多数的Skyline元组。
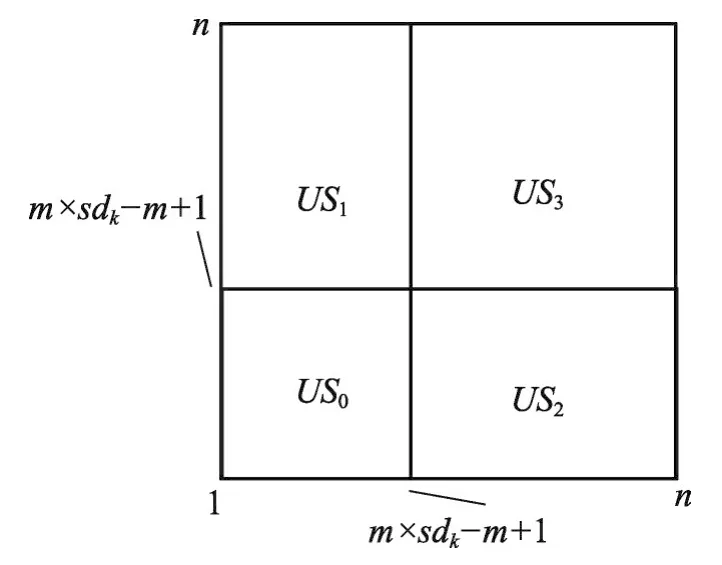
Fig.2 Illustration of pruning region of pruning rule图2 剪切规则剪切区域的图示
6.2 阶段2:计算支配分数
在获得查询结果的候选元组后,RSTS算法在阶段2计算每个候选元组的支配分数,从而确定支配分数最大的k个候选元组。
在6.1节,分析的RSTS算法的阶段1的扫描深度的上界是。类似的,根据6.1节的分析可以确定,∀cad∈STCAD,cad.PIi<m×sdk-m+1,即cad.PIi的可能最大值是m×sdk-m。那么,在阶段2,要计算cad的支配分数,需要读取的表PT的扫描深度可能最大值是M×(m×sdk-m),来确定不能被cad支配的元组数量。很明显。在阶段1结束条件满足时,RSTS仍然需要继续读取表PT的元组来计算STCAD中的候选元组的支配分数。
对于阶段1读取的元组,一个直观的选择是维护这些元组,那么在阶段2时就可以从阶段1结束的位置开始继续读取元组,从而减少I/O费用。但是在实际实现时,阶段1维护元组所带来的更大的内存费用超过了内存维护读取元组而减少的阶段2的I/O费用,而且在阶段1读取的数据有很大部分已经在内存中缓存,再次读取这些数据的效率会较高。因此,本文采用的方法是,不维护阶段1读取的元组,阶段2从头开始重新读取表PT来计算候选元组的支配分数。
阶段2执行前,令STCAD中的所有候选元组的支配分数都是n,即∀cad∈STCAD,dom(cad)=n。令pt是阶段2中当前读取的PT元组,那么∀cad∈STCAD,如果cad不支配pt,dom(cad)的值自减1。很明显,阶段2的实际扫描深度计算如下:
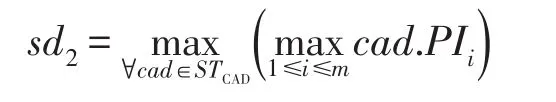
如果pt.MPIL>sd2,∀cad∈STCAD,无法被cad支配的元组都已经获得,因此当前的dom(cad)值就是cad的支配分数。阶段2结束,RSTS算法返回STCAD中支配分数最大的k个候选元组。
7 实验评价
7.1 实验设置
本节评价RSTS算法性能。实验环境为Lenovo ThinkCentre M8400(Intel®CoreTMi7-3770 CPU@3.40 GHz(8 CPUs)+32 GB内存+64位Win 7操作系统+1 TB硬盘)。实验比较RSTS算法、RB算法和BA算法的性能。
在实验中,从以下几方面来评价RSTS算法的性能:元组数量(n)、结果数量(k)、使用属性数量(m)、所有属性数量(M)。实验将在合成的数据集上执行,实验参数设置如表1所示,并在真实数据集HIGGS上执行。
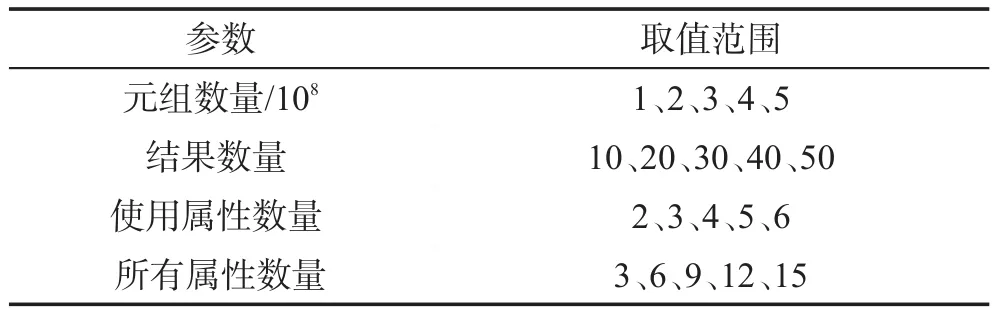
Table 1 Table of parameters setting表1 实验参数设置表
7.2 实验1:元组数量的效果
给定m=3,M=12,k=10,实验1评价RSTS算法在不同元组数量的性能。如图3(a)所示,RSTS算法比BA算法快57.128倍,这可以证明RSTS算法的高效性。这一个数量级的加速比来自于更小的内存计算费用和磁盘读写费用。RB算法的执行效率比RSTS算法差得多,其执行时间甚至超过BA算法。这是由于在读取由R-tree索引的海量数据时,每次读取叶节点的数据都会引起一次磁盘随机寻道操作,从而严重影响算法的执行效率。三种算法在其执行阶段读取的元组数量如图3(b)所示。其中,RSTS算法读取的元组数量是阶段1和阶段2中读取的元组数量之和。如图3(b)所示,RSTS算法读取的元组数量是BA算法读取元组数量的4.349%,是RB算法读取元组数量的10.50%。图3(c)给出了RSTS算法在阶段1和阶段2的实际扫描深度(P1和P2)及其理论扫描深度(P1(T)和P2(T))。可以看到,阶段1和阶段2的扫描深度基本符合理论结果。RSTS算法在阶段1中提出的剪切规则的剪切效果如图3(d)所示,剪切效果不小于0.924,绝大多数的Skyline元组都可以被直接丢弃,从而减少了阶段2的计算费用。也给出了理论的剪切效果,可以看出,实际剪切比超过了理论剪切比,但是其变化趋势基本符合理论结果。
7.3 实验2:结果数量的效果
给定m=3,M=12,n=108,实验2评价RSTS算法在不同结果数量的性能。如图4(a)所示,RSTS算法比BA算法快12.308倍。随着k值的增长,RSTS算法的执行时间增长较快,BA算法的执行时间则基本不变,而RB算法的执行时间仍然比较长。类似的变化趋势也反映在图4(b)中,但是RSTS算法读取的元组数量是BA算法读取元组数量的15.43%,是RB算法读取元组数量的33.94%。RSTS算法的扫描深度在图4(c)中给出,可以看到,在阶段1,RSTS算法的扫描深度不发生变化,这是因为阶段1其实就是计算Skyline结果的过程。但是,更大的k值使得RSTS算法在阶段1结束时需要维护更多的候选元组,这也增加了阶段2的扫描深度。如图4(d)所示,随着k值的增大,RSTS算法剪切操作性能也逐渐下降,这也符合理论分析的结果。
7.4 实验3:使用属性数量的效果
给定k=10,M=12,n=108,实验3评价RSTS算法在不同使用属性数量的性能。如图5(a)所示,RSTS算法比BA算法快90.661倍。随着m值的增大,Skyline结果数量也呈指数级增加,这使得三种算法的执行时间都快速增长。实验3并没有报告RB在m=6时的执行时间,因为在m=5时RB的执行时间已经超过257 500 s,根据其变化趋势,在m=6时执行时间会非常长。如图5(b)所示,RSTS算法读取的元组数量是BA算法读取元组数量的10.11%,是RB算法读取元组数量的45.27%。图5(c)给出了RSTS算法的扫描深度,可以看到,阶段1和阶段2的扫描深度都随着m值的增大而快速增长,基本都符合理论分析的结果。RSTS算法在阶段1的剪切效果如图5(d)所示,大多数的Skyline结果元组都可以被剪切,减少了RSTS算法需要维护的候选元组数量。
7.5 实验4:所有属性数量的效果
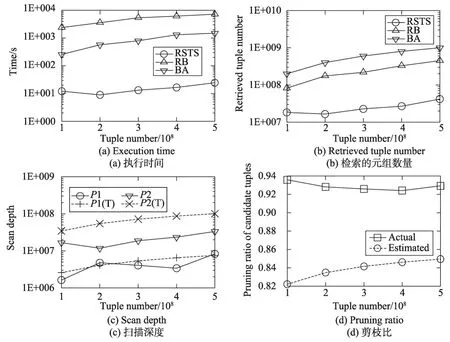
Fig.3 Effect of tuple number图3 元组数量的效果
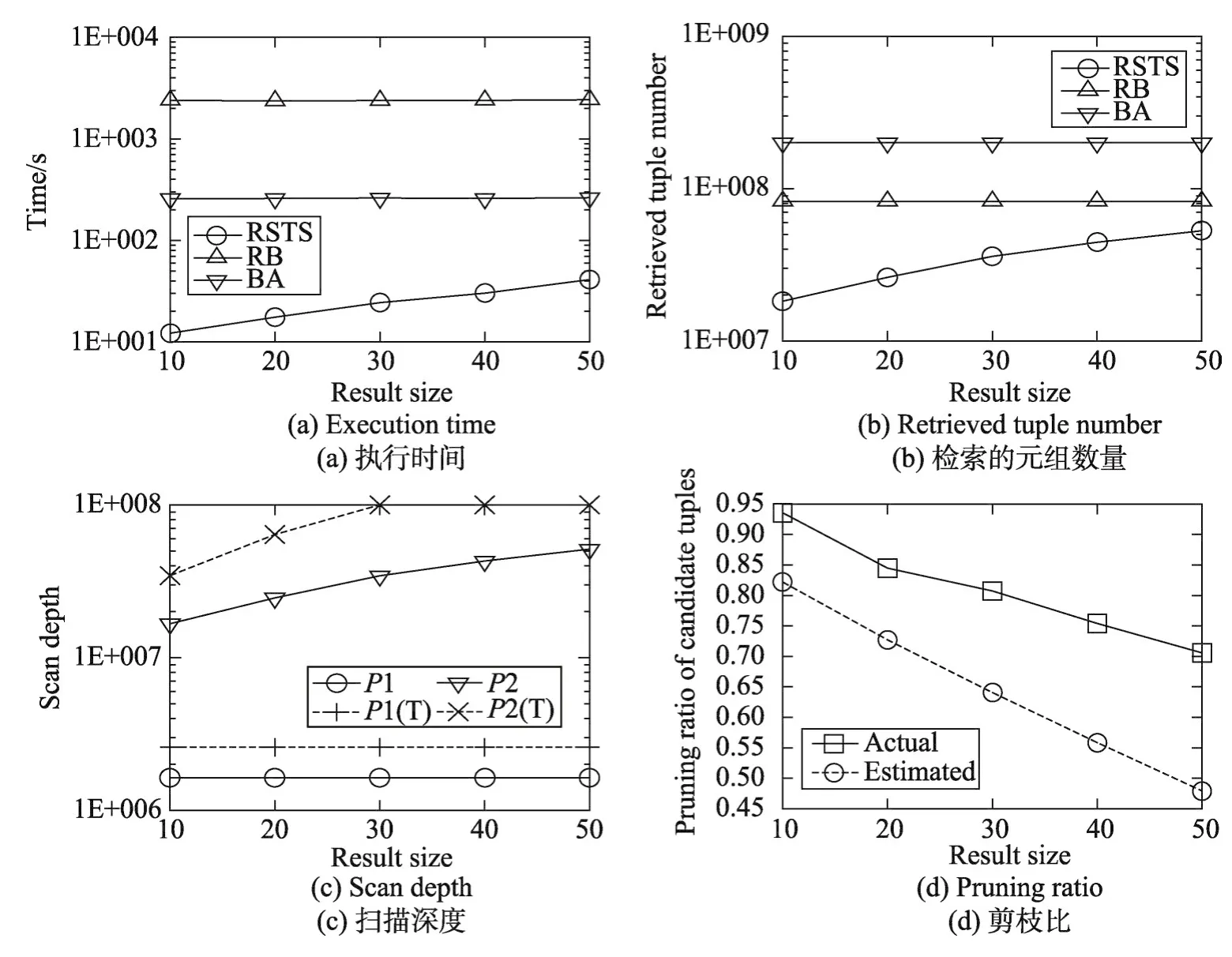
Fig.4 Effect of result size图4 结果数量的效果
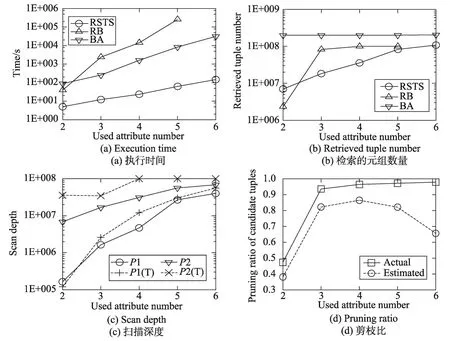
Fig.5 Effect of used attribute number图5 使用属性数量的效果
给定k=10,m=3,n=108,实验4评价RSTS算法在不同所有属性数量的性能。如图6(a)所示,RSTS算法比BA算法快120.186倍,而RB算法的执行时间比BA算法的还长。随着M值的增加,BA算法的执行时间增长幅度并不大,而RSTS算法的执行时间则快速增长。M值的变化使得每个元组的长度发生变化,但是这并不影响BA算法在计算top-kSkyline结果时读取的元组数量,由于预排序表的构建方法,较大的M值影响了RSTS算法需要读取的元组数量。读取的元组数量的结果如图6(b)所示,RSTS算法读取的元组数量是BA算法读取元组数量的2.978%,是RB算法读取元组数量的6.638%。RSTS算法的扫描深度如图6(c)所示,可以看到,随着M值的增加,RSTS算法在阶段1和阶段2的扫描深度都增加。RSTS算法的剪切比例如图6(d)所示,绝大多数的Skyline元组都可以被剪切。
7.6 实验5:真实数据集的效果
真实数据集HIGGS来自于UCI Machine Learning Repository。该数据集包含11 000 000个元组以及28个属性。选择前3个属性来计算top-kSkyline结果。在实验5中,通过不同的结果大小来评估RSTS的性能。如图7(a)所示,RSTS比BA快7.08倍,比RB快77.78倍。随着k值的增加,RSTS的执行时间显著增加,而BA和RB的执行时间基本保持不变。在实验5中,无论k取何值,BA和RB算法中仍然需要先计算出Skyline结果,然后计算其支配分数。如图7(b)所示,RSTS读取的元组数量是BA算法读取元组数量的23.53%,是RB算法读取元组数量的46.95%。RSTS检索到的元组数量随着k值的增大而增加,因为RSTS需要检索更多的元组来确定top-kSkyline结果,图7(c)也说明了这一点。如图7(d)所示,随着k值增加,剪枝规则的剪枝效果变差,从0.872减少到0.674,这与理论结果相符。
8 结论
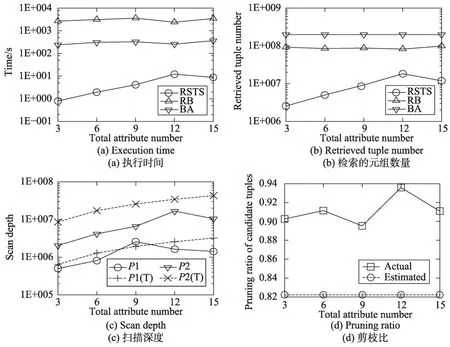
Fig.6 Effect of total attribute number图6 所有属性数量的效果

Fig.7 Effect of real data set图7 真实数据集的效果
本文考虑海量数据的top-kSkyline查询问题,提出一个新的基于表扫描的RSTS算法,该算法利用对预排序表的顺序扫描来计算top-kSkyline结果。RSTS算法的执行包括两个阶段,阶段1扫描预排序表并维护候选元组,阶段2计算候选元组的支配分数并返回查询结果。本文的分析发现,RSTS算法具有早结束特点,并给出早结束操作的扫描深度的理论分析。RSTS算法在阶段1利用有效的剪切操作来减少需要维护的候选元组,本文给出的理论剪切分析表明,绝大多数的Skyline元组都可以被丢弃。实验结果表明,RSTS算法可以有效计算海量数据top-kSkyline结果。
