基于双IRS辅助的毫米波MIMO通信信道估计
2022-04-01李祥森
李祥森
(1.南京邮电大学 电子与光学工程学院/微电子学院,江苏 南京 210023;2.射频集成与微组装技术国家地方联合工程实验室,江苏 南京 210023)
0 引言
在传统通信系统中,信道估计是至关重要的一项技术。特别在5G毫米波多输入多输出(Multiple-Input Multiple-Output, MIMO)通信系统中,需要对所发射的信号进行波束形成及预编码操作,以获得完美的信道状态信息为重要前提。由于6G的研究热潮兴起,在考虑毫米波信号具有穿透能力差、阴影衰落等特点[1]的前提下,在通信系统中引入智能反射面(Intelligent Reflecting Surface,IRS)这一新型无源器件来达到重新配置信道环境[2],降低整体系统功耗[3]的效果,从而提高无线通信系统的频谱效率和能量效率[4]。然而,由于目前的IRS上元素个数较多,其与基站和用户之间形成的通信信道维数较大,导致整个信道估计的过程较为复杂,因而研究人员主要以降低信道估计的复杂性为目标进行研究。
在文献[5-6]中,IRS的完美信道状态信息(Channel State Information,CSI)反射系数优化得到广泛的研究,验证了IRS能够有效提高系统吞吐量,由此可见得到完美信道状态信息的重要性。然而现实中获得精确的CSI在实践中相当具有挑战性。尤其是为了降低成本,IRS通常不配备任何射频(Radio Frequency,RF)链,导致不能执行任何传统基带处理功能。因此,不能通过传统的基于训练的方法来分别估计基站(Base Station,BS)-IRS和IRS-用户。相反,只能根据用户/BS发送的训练信号来估计连接的用户-IRS-BS信道。在基于IRS的毫米波MIMO通信系统中,信道估计的复杂性主要在于两个方面:一方面,IRS在BS与UE之间的级联信道维度较高;另一方面,则是IRS元件的被动特性提高了信道估计的复杂性。
在先前的研究工作中,研究人员针对IRS的元件本身做了一定设计和优化。文献[7]中针对单用户通信系统,提出了基于开关状态控制的信道估计策略,在每个时隙仅打开一个IRS元素,从而使得估计用户的反射信号不受其余反射信道的影响。在这种策略下,N个时隙足以在没有接收机噪声的情况下完美地估计用户的所有反射信道状态信息。在文献[8]中,作者为了提高RIS辅助的通信系统的频谱效率,基于遗传算法(Genetic Algorithm,GA)设计出一个接近最优的RIS移相器。在此基础上,可以更有效率地估计信道状态信息。
考虑IRS元件的被动特性及在实际中周围的环境。在文献[9]中,提出了一个IRS辅助的多用户上行通信系统。其中多个单天线用户借助一个IRS与一个多天线BS进行通信,IRS元件被动地反映用户发送给BS的导频序列,使BS能够估计与IRS相关的CSI。文献[10]针对高速轨道上大规模天线正交频分复用(OFDM)通信系统研究并设计了两种切实可行的正交频分多路复用(Orthogonal Frequency Division Multiplexing, OFDM)通信系统的上行和下行信道估计器。通过离散傅里叶变换(DFT)来估计每个上行路径的初始到达角(Angle of Arival,AoA)和分离角(Angle of Department,AoD)信道增益信息,然后通过角度旋转技术和建议的导频设计进行细化估计。文献[11]中研究了实际具有离散相移的正交频分复用(OFDM)系统中的信道估计,与之前假设IRS具有理想反射模型的工作不同,通过考虑实际IRS响应的振幅-相移-频关系来进行信道估计以降低最小均值误差。
在基于IRS的通信系统进行信道估计时,有研究人员引入了传统的压缩感知方法和新型的数值方法,并取得一定的成果。文献[12]中提出了一种基于压缩感知(Compressed Sensing,CS)的毫米波大规模MIMO系统信道估计(Channel Estimation,CE)解决方案,利用大规模阵列在毫米波的角信道稀疏性改进信道估计,降低了导频开销。文献[13]中设计了一种基于自适应CS的算法,结果显示该算法具有较小的迭代次数和较高的成功概率,有效地估计了毫米波信道的参数。文献[14]提出一种基于低复杂度压缩感知(CS)的信道估计方法并利用太赫兹通信信道的稀疏性,将信道估计问题转化为原始信号恢复问题,最终实现了信道估计。文献[15]中表明接收信号遵循并行因子张量模型,可以利用封闭或迭代地估计所涉及的通信信道,其数值结果证实了所提出信道估计方法的有效性,并强调了所涉及的权衡。
基于上述考虑,提出一种基于双IRS辅助的毫米波单用户MIMO下行无线通信的系统模型,通过借助多个IRS起到分集复用的效果进而提高信道估计的准确度。仿真结果显示,双IRS归一化均方误差性能优于单IRS,保证了整个通信系统的归一化均方误差性能。
1 系统模型
图1给出了基于双IRS辅助的毫米波单用户MIMO下行无线通信的系统模型。设定基站Nt根发射天线,单用户为Nr根接收天线,智能反射面分别为IRS1和IRS2,且每个智能反射面配置被动元件数为NI个。基站至IRS1和IRS2的信道分别为G1,G2∈NI×Nt,IRS1和IRS2至用户的信道分别为Nr×NI。考虑基站与用户间存在阻挡物,因此不存在基站至用户的视距路径。而且由于智能反射面本身是大量的无源器件,经过其反射的信号仅能通过相位的调整改变传播方向,对其幅度增益没有效果,因此衰减程度较大,双IRS之间基本不存在通信链路。在实际通信场景中,因为不同智能反射面反射路径的距离差往往很小,可以认为远小于码元周期,因而此通信系统仍为一个窄带模型,到达用户端接收的信号为各通信链路信号的叠加。

图1 双IRS毫米波通信信道模型Fig.1 Double IRS millimeter wave communication channel model
在基于双IRS的毫米波通信系统中,为了符合实际情况,智能反射面均采用均匀方形阵列(Uniform Planar Array,UPA)结构,而基站与用户端使用均匀线性阵列(Uniform Linear Array,ULA)结构,则毫米波信道模型如下:
(1)
(2)
(3)
(4)
式中,αl1,βl2,αl3,βl4表示不同信道路径的复增益系数,γ和φ表示智能反射面的方位角与仰角,θ表示基站与用户的分离角/到达角,a和b表示阵列响应向量。对于阵列响应向量a(θ,φ)满足一定性质,即
a(θ,φ)=ax(θ,φ)⊗ay(θ,φ)。
(5)
对于UPA模型而言,阵列响应向量可表示为:
(6)
其中,M×N表示基站与智能反射面/智能反射面与用户双方的天线数和智能反射面元件数之间的乘积。为了使该式更加结构化,可以进一步表示为:
(7)
针对此通信场景,给出了信道估计过程中的估计协议。如图2所示,信道估计过程中将所需发射信号分为B块,每个块中存在T个时隙,且每个时隙之间的发射信号彼此是正交的。

图2 信道估计协议Fig.2 Channel estimation protocol

(8)
式中,Sb∈Nt×T表示为在b块中包含所有T时隙的发射信号矩阵,Nb=[n1,n2,…,nT] ∈Nr×T表示为在单个块中的加性高斯白噪声(Additive White Gaussian Noise,AWGN),对于∀t∈{1,2,…,T}而言由Nr×1叠加得到。为了将信道突出显示,去除发射信号的影响,由于在单个块中每个时隙的发射信号彼此正交,满足对式(8)解耦发射信号则得:
(9)
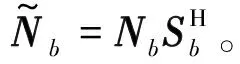
因此在单个块中需要估计的信道矩阵为:
(10)
2 压缩感知信道估计
由于毫米波信道的稀疏性,考虑将毫米波信道估计问题转换为压缩感知的恢复稀疏矩阵模型。但在基于智能反射面的通信系统中,由于智能反射面的无源被动特性,一般将其作为一个黑箱系统进行级联估计。因此,在使用压缩感知理论时需要先对原始通信系统模型进行信道合成得出压缩感知的形式,然后再采用压缩感知算法进行性能评估。
传统的压缩感知理论表明信号如果是可压缩的或在某个变换域内是稀疏表示的,那么就可以用一个与变换基不相关的观测矩阵将变换所得的高维信号投影到一个低维空间上,然后通过求解一个优化问题就可以从这些少量的投影中以高概率恢复出原始信号,并且该投影包含重构信号的足够信息。其常见的数学模型公式为y=Kx+ε,其中,K表示为感知矩阵,x表示为稀疏向量,ε表示为系统误差。

(11)
(12)
(13)
(14)

Σ1,Σ2∈MG×NG,Γ1,Γ2∈NG×MG为仅具有和稀疏路径数等同的非零元素的稀疏矩阵,其中的非零元素位置揭示了对应着第l条路径的两个码字(分离角和到达角)及其对应的增益。其中码字数目关系满足MG=MG,x×MG,y,NG≥Nt。
在同一个块中需要估计的信道模型通过式(11)~式(14)代入到式(10) 转化为下式:
(15)

进一步,利用矩阵向量化和克罗内克积性质[16],得出矩阵的稀疏表达形式为:
(16)

(17)
对式(17)进一步矩阵拉直运算,则得最终压缩感知模型,即:
(18)

(19)
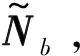
文献[17]中提出当使用压缩感知算法时,想要提高恢复信息的精度,需要提高待估计稀疏向量的非零元素个数的上界,并与感知矩阵的自相关度有着反比例的关系。换言之,如果想要提高恢复的精度,需要降低感知矩阵的自相关度。因此,需要对比双IRS与单IRS所得到的感知矩阵的自相关度大小,以此为依据判断引入双IRS后的信道估计性能。首先给出自相关度的定义式如下:
(20)
式中,Kj和Ki表示感知矩阵K的第i和第j列向量。


图3 信道估计因子信息传递模型Fig.3 Channel estimation factor information transfer model
传统的GAMP算法通过高斯近似,并引入输入、输出估计函数。然而因为存在p(Hj)信道先验信息,在实际中接收端无法确定获得信道先验以及先验分布的各项参数,类似一个黑箱系统,无法确定内部的参数。并且,该算法对信道的估计是针对全支撑集,在低信噪比的前提下易受噪声影响,难以对其稀疏成分实现准确估计。由于匹配追踪根本在于贪婪思想,逐步地迭代选择局部最优解以更新支撑集[18],因此在传统的GAMP算法上结合该算法确定信道的稀疏支撑集,可以有效提高其收敛性,降低了对信道先验信息的要求,同时减少了数据存储,降低了信道估计的导频开销。其算法流程如算法1所示。

算法1 基于匹配追踪的GAMP算法Input:y=Kx+ε,根据式(20)知K=(Tυ∗b)TU{},x=vec(Λ-)。稀疏度设置为P。Output:x^(t+1)1.Initial:残差初始值为u(t=1)=y,支撑集为∅,K为∅,t= 1;2.计算出矩阵列与残差的相关性KHu(t),并将相关系数最大的那一列的索引地址赋给i。3.通过使用传统的GAMP算法迭代出重构信号x^i(t+1),然后使用重构信号更新残差u(t=1)=y-Kx^(t),通过迭代收敛条件x^i(t+1)-x^i(t)x^i(t)≤δ判断是否程序停止,若满足,则更新支撑集。4.依次迭代,k=k+1,如果k≤p,则返回执行第2步,否则输出最终的估计值输出x^(t+1)。
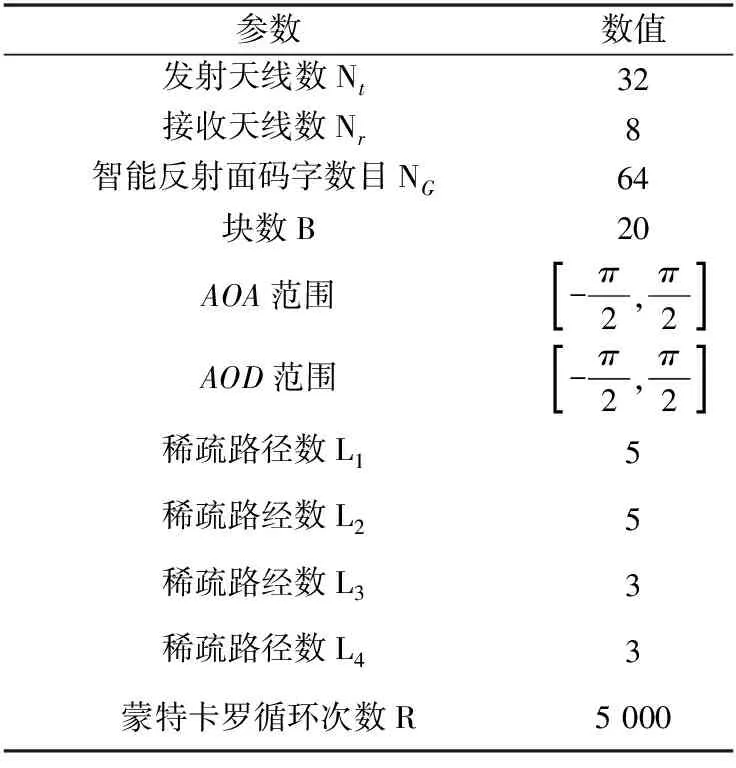
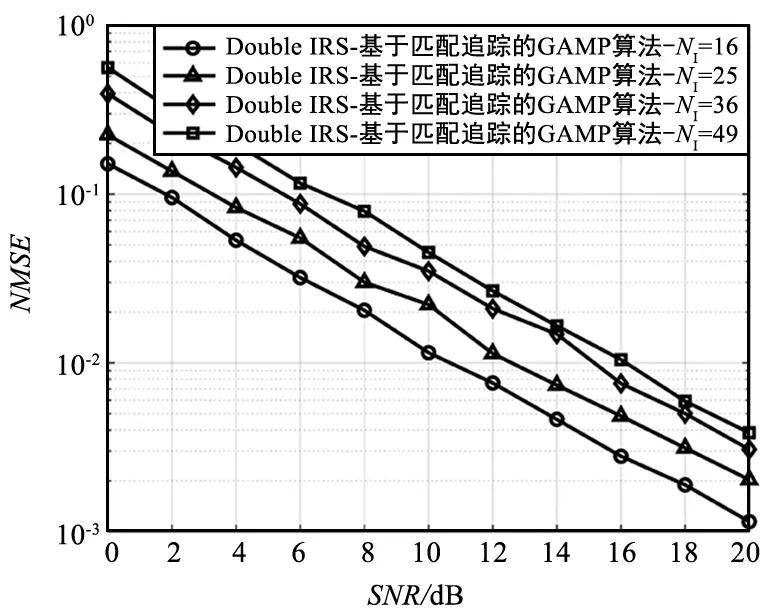
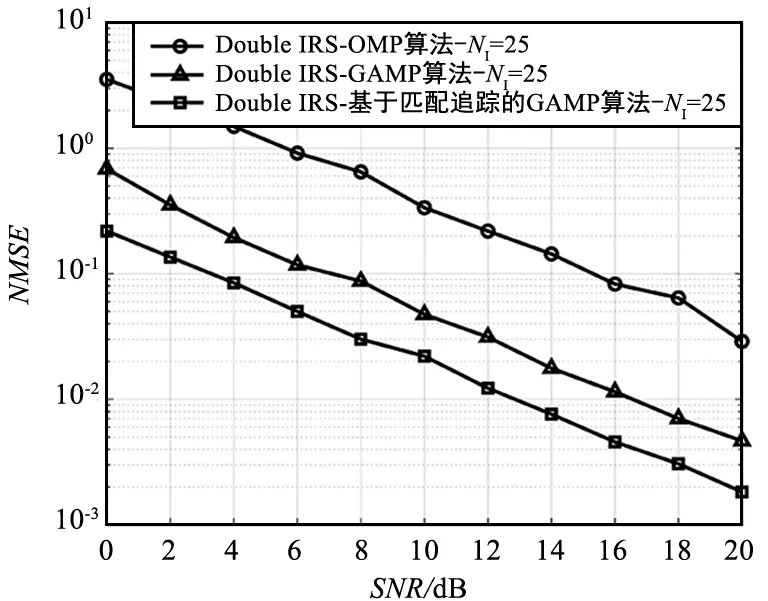
基于匹配追踪的GAMP算法是根据贪婪思想并建立在支撑集的基础上,进一步利用传统的GAMP算法迭代出重构信号。在传统的GAMP算法过程中每次迭代都需要计算出稀疏向量x的全部元素,计算复杂度高为O(MN)。而基于匹配追踪的GAMP算法只需要计算匹配追踪到的第k个值,其中在前k-1次迭代中使用omp匹配追踪确定稀疏支撑集, 仅进行一次估计,而在第k次时仅需迭代较少次数即可提高恢复精度,计算复杂度降低为O(Mk),其中k< 仿真场景设置为基站和用户多根天线,且IRS1和IRS2的相位对角矩阵在同一个块中保持相同,使用评价指标归一化均方误差(Normalized Mean Square Error, NMSE)来评价估计性能,表达式如下: 如图4所示,在控制智能单元数相同的前提条件下,得出双IRS与单IRS之间的归一化均方误差性能对比关系图。通过仿真图表明双IRS的归一化均方误差率性能显著优于单IRS的归一化均方误差率性能,并且随着信噪比的升高归一化均方误差继续下降,仿真结果验证了理论判断依据。 表1 仿真参数 图4 双IRS与单IRS的归一化均方误差性能对比Fig.4 Performance comparison of normalized mean square error between double IRS and single IRS 图5 智能反射面单元数与归一化均方误差性能的关系Fig.5 Relationship between the number of intelligent reflector units and the performance of normalized mean square error 为了验证本文中的算法性能,和其他现有压缩感知算法进行了归一化均方误差性能对比。图6显示在控制智能反射面单元数相同的条件下,使用基于匹配追踪的GAMP算法显著优于OMP算法和GAMP算法,并且降低了整个系统的计算复杂度。 图6 压缩感知算法归一化均方误差性能对比Fig.6 Performance comparison of normalized mean square error of compressed sensing algorithms 提出了IRS在毫米波通信信道估计中应用的新场景,并在理论上推导分析引入双IRS后的信道估计性能。考虑毫米波信道的稀疏性,将引入双IRS后的信道模型转换为压缩感知形式,并使用基于匹配追踪的GAMP算法进行优化处理以降低信道估计的复杂度。仿真结果表明,双IRS归一化均方误差性能优于单IRS。同时使用基于匹配追踪的GAMP算法有效降低了计算复杂度,保证了整个通信系统的性能,对于IRS在毫米波通信场景中的应用进行了拓展。未来进一步工作研究将致力于:① 使用流行理论优化算法对信道估计性能进行改进;② 采用双混合智能反射面结构单独估计每一条信道,提高信道估计的准确度。3 仿真结果与分析


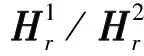
4 结束语
