基于分级策略和改进相位相关的SAR影像配准

何 伟，徐卓揆，刘佳斌

（1.长沙理工大学 交通运输工程学院，湖南 长沙 410114；2.长沙理工大学公路地质灾变预警空间信息技术湖南省工程实验室，湖南 长沙 410114）

InSAR可全天时、全天候快速获取大面积高精度的地表三维信息，已成为获取高精度数字表面模型的重要技术手段[1]。目前，国内外对InSAR图像配准进行了深入研究，并提出了多种有效的处理算法，主要包括最大相关系数法、最大频谱法、点目标配准法、雷达几何法[2-4]和最小二乘配准法。几何配准法精度较低，往往用于初始配准。传统基于模板的配准方法不仅搜索范围大，而且需要逐行逐列移动配准窗口计算相关测度，从而引进了大量重复运算，导致运算效率低下，且斑点噪声也增加了配准难度。亚像素配准往往是通过各种测度曲线拟合或像素插值的方法确定。曲线拟合即使在信噪比较高的情况下也只能达到0.15～0.2像素[5]。基于插值的方法[6-7]精度很高，但插值算法重采样计算量较大，也容易陷入局部多极值的情况。最小二乘配准法则需要准确的初值，往往需要跟其他方法结合使用。

相位相关法是一种在傅里叶域求解整数偏移参数的方法。与传统的图像配准方法相比，相位相关具有良好的精度和可靠性等优势[8-9]，经过扩展后，能进行亚像素级配准。然而，对于SAR影像来说，在较大范围内直接采用相位相关法的精度不高，因为在较大范围内并不存在一致的偏移量。本文提出了一种基于分级配准策略和改进局部相位相关的SAR影像快速配准方法。首先对像对进行粗配准，再对影像进行分块，然后分别利用相位相关法和改进的相位相关法对分块图像进行整像素配准和亚像素配准，最后重采样得到配准结果。该方法避免了在较大范围直接使用相位相关法，且提高了传统相位相关法的亚像素配准精度。

1 分级配准流程

利用相位相关法进行SAR影像配准时，为了避免大范围相位相关配准的限制，本文基于分级配准策略进行相位相关配准；并在局部亚像素配准时，对传统相位相关法进行了改进，以提高配准的可靠性和效率。相位相关法分为频域解法[10]和空域解法[11]，频域解法在窗口较大时SVD分解会产生较大的运算量，因此本文采用空域解法。

分级配准流程如图1所示：①全局粗配准，通过几何配准进行粗配准、截取重叠区域；②局部精配准，在主影像上均匀分块、布设控制点，以控制点为中心确定配准模板；③重采样得到配准结果。首先通过相位相关法直接定位得到整像素偏移；然后利用改进的相位相关法进行亚像素配准，即以相关峰为测度、曲线拟合改正偏移量双迭代求取亚像素位移。该方法收敛速度快、定位范围大、可靠性高、精度高，对于噪声的鲁棒性较强，在低相关地区效果更稳健。

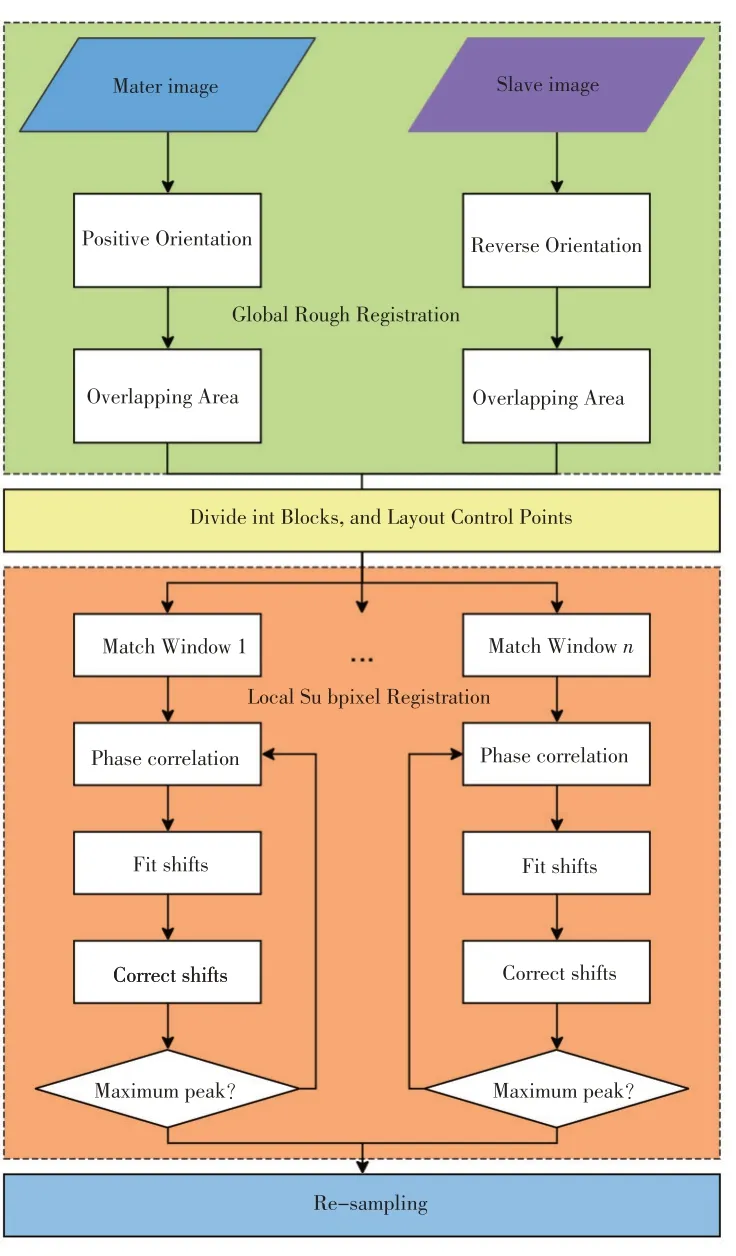
图1 分级配准与基于改进相位相关的亚像素配准流程图

2 研究方法

2.1 几何配准

几何配准是目前SAR影像使用最多的概略配准方法。其原理是根据SAR影像独特的成像规律，利用轨道信息和成像参数计算主、辅影像的偏移量。与相关配准方法相比，几何配准不受影像大小、相干性的影响，可靠性较高。

首先利用卫星轨道状态矢量和成像参数构建R-D模型（包括多普勒条件方程、斜距方程和地球椭球方程）；再基于主影像中心像素的经纬度，通过求解主影像R-D模型得到其地面坐标；然后将该坐标值代入辅影像R-D模型反向求解像素坐标；最后得到两幅影像的大致偏移量。相关方程可表示为：

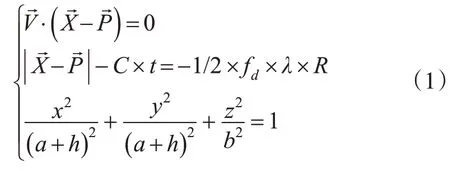
R-D模型的解算属于非线性方程的求解，本文采用牛顿迭代法，配准精度可达10～20个像素。

2.2 改进的相位相关亚像素配准方法

2.2.1 相位相关法基本概念

频率域的相位相关法是利用傅里叶变换偏移不变性对图像进行配准的方法。由傅里叶偏移性质可知，图像在空间域产生偏移，在频域中频谱大小不会发生改变，但相位会相应的产生线性变化[12]。利用这一性质可以估计偏移参数[13-14]，假设两幅图像f2(x,y)和f1(x,y)只存在偏移参数(x0,y0)，则它们的关系可表示为：

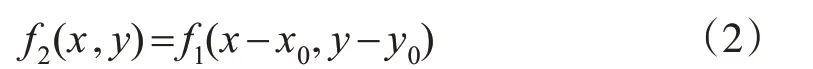
定义它们对应的傅里叶变换分别为F2(u,v)和F1(u,v)，则有：

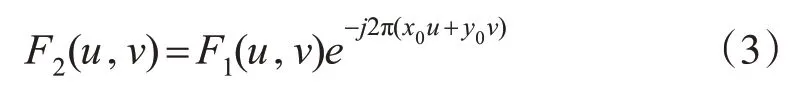
定义它们的归一化互功率谱为：

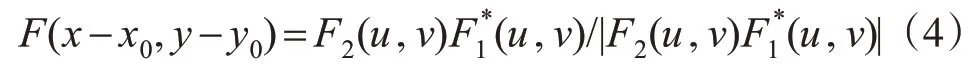
式中，*为取复数共轭；|·|为复数取模。

互功率谱函数的傅里叶反变换是一个二维的Dirichlet函数[11'15]。在没有噪声的情况下，该函数在(x0'y0)处的值为1，其他处均几乎为0，因此只需通过F的反变换峰值坐标即可确定偏移参数。

2.2.2 传统亚像素相位相关法

图像的亚像素移动是由于图像的采样率低、采样间隔过大（降采样）产生的[16]。例如，将图像移动12个像素得到另一幅图像，再把两幅图像10倍下采样，则下采样的两幅图像之间的相对位移量为1.2，由此产生亚像素位移。Forooh H[11]等通过理论分析得出，在信号为带限的情况下，降采样后互功率谱的傅里叶反变换得到的二维Dirichlet函数在降采样前有唯一的峰值，该峰值处于现在的主峰与侧峰之间。

Dirichlet函数可用sinc函数近似，Forooh H[11]等基于此推导了亚像素的计算公式，则沿X轴的亚像素位移量为：

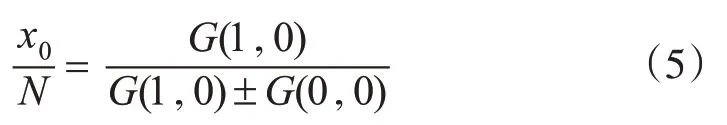
式中，G(0,0)为主峰；G(1,0)为X轴方向的侧峰；N为下采样倍数。

同理可得Y方向的亚像素位移量为：

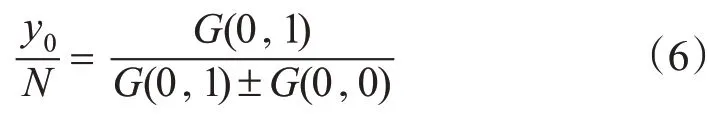
2.2.3 改进的亚像素相位相关法

式（5）和式（6）采用的方法本质上来讲是基于sinc函数的拟合，由于受到SAR图像噪声等多种因素影响，互功率谱的傅里叶反变换并不完全满足sinc函数，且该方法只用到了一个侧峰值，忽略了两个侧峰之间的关系。实验表明，对于偏移量较小的情况，估计结果往往偏大，若采用该方法多次迭代逼近则容易陷入不能收敛的问题。Dirichlet函数在降采样前有唯一的峰值，降采样后相关峰最大的位置即为该峰位置，即当完成精确配准时，相关峰应达到最大。两个无噪声的模板在亚像素范围内，相关峰随偏移量的变化曲线如图2所示，可以看出，相位相关法本质上是寻找相关峰的极值位置。从理论上来讲，该曲线是一条关于垂直于横轴0坐标直线的对称曲线，因此也可以由一条二次曲线近似。

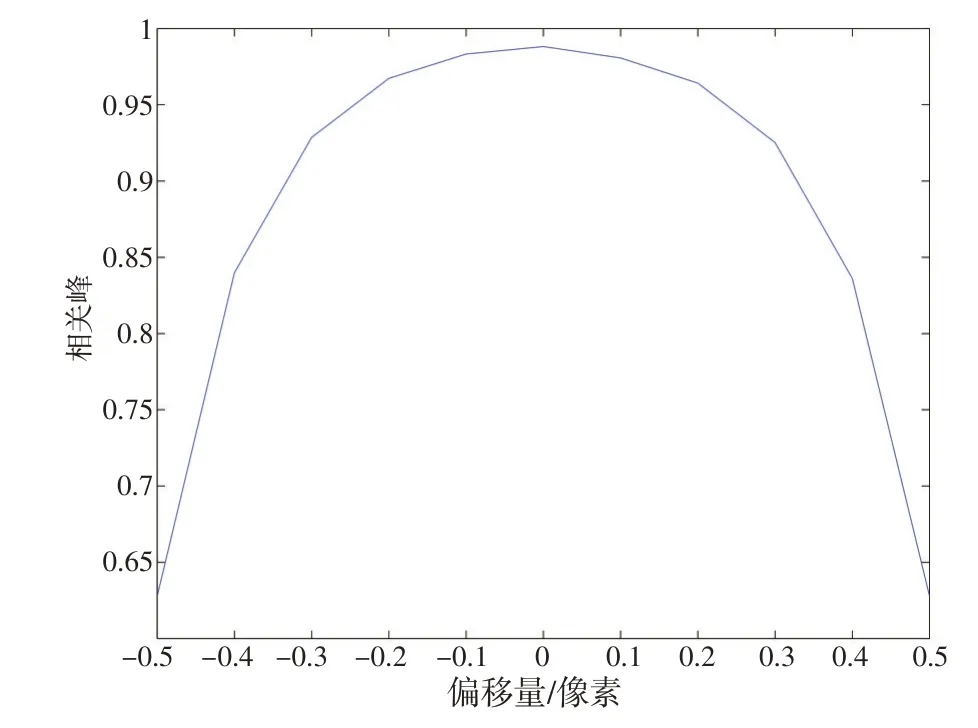
图2 相关峰随偏移量的变化曲线

为了避免传统方法在亚像素领域运用SAR配准的缺陷，本文以相关峰为测度，通过二次曲线拟合相关峰并迭代逐步逼近来求解亚像素偏移量。在实现像素级配准后，再分别求解距离向和方位向的亚像素，以一个方向为例，利用二次曲线拟合两个侧峰和一个主峰求解极值，得到亚像素偏移量，改正偏移量重采样后再次使用相位相关直到相关峰达到最大。具体操作流程为：①利用配准模板和配准影像通过相位相关法得到主峰和两个侧峰值及其对应的像素坐标；②基于主峰和侧峰的3对像素坐标，利用二次曲线函数进行拟合，得到拟合函数的最大值及其对应坐标，进而得到偏移量；③改正偏移量，配准影像经过重采样后得到新的配准影像；④回到步骤①直到相关峰两次迭代结果小于0.01个像素，累计的偏移量则为最终偏移量。

在多种因素的影响下，Dirichlet函数可能不再近似于sinc函数，传统的相位相关法将无法精确定位亚像素偏移，多次迭代也经常无法收敛；而这种通过二次曲线拟合逐步逼近到最大值位置的方法可忽略原函数的具体形状，通过多次迭代在保证配准精度的前提下，能简单有效且快速收敛，不会增加太多的运算量。

2.3 重采样

本文得到控制点的映射关系后，采用多项式拟合控制点，采用二次多项式进行全局拟合[17]。

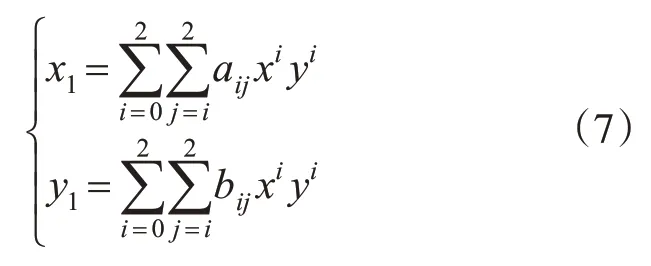
式中，x、y为主影像上控制点的像素坐标；x1、y1为配准后辅影像的对应点坐标。

代入所有控制点，采用最小二乘法求解得到映射模型；再计算主影像所有像素对应的辅影像坐标，最后采用双三次卷积法插值重采样。

2.4 配准质量评价

通常评价SAR影像配准质量的指标为相关系数和多项式拟合均方根误差（RMSE）。

SAR相关系数的无偏估计包含相位校正项，在样本足够多、相关性较好时估计质量较好，但实际操作比较困难，特别是在低相关地区效果不好。本文采用相关系数快速估计法[17]，计算公式为：

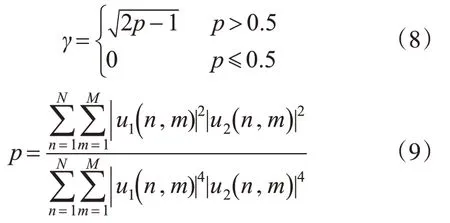
本文将预设的控制点代入二次多项式模型计算残差并计算RMSE，计算公式为：

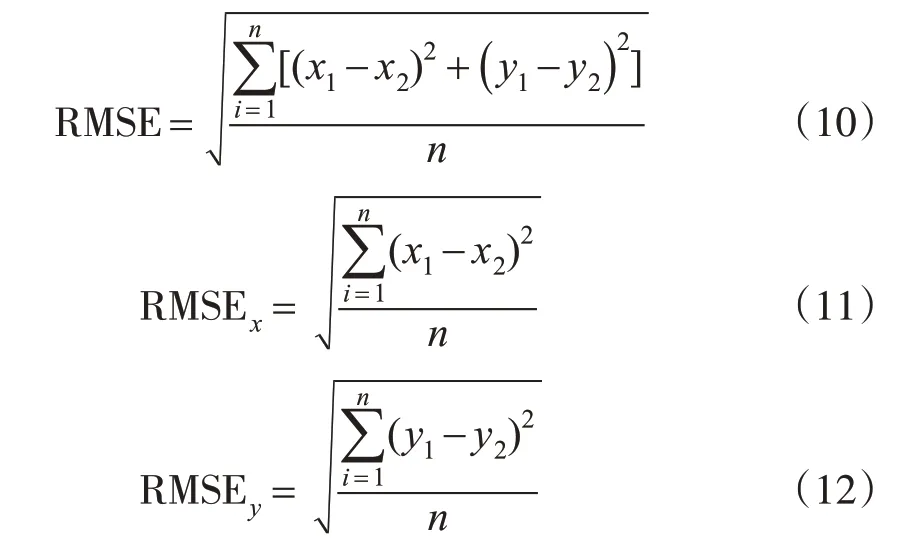
式中，RMSEx和RMSEy分别为X、Y方向上的RMSE；(x1'y1)为通过配准得到的控制点辅影像上的坐标值；(x2'y2)为由多项式模型计算得到的坐标值。

3 实验结果与分析

3.1 方法性能分析

实验采用两幅日本千叶市地区ENVISAT ASAR Single Look Complex数据，VV极化，入射角为23°，覆盖范围约为20 km×20 km。采用ENVI软件导出数据，主影像大小为5 125×2 435，辅影像大小为5 145×2 436，如图3所示，数据存储格式2×32比特复数。

图3 实验主、辅影像强度图

实验采用一台Intel Core i7处理器、GTX965M显卡、8 GB内存的笔记本电脑在Matlab上实现。在主影像上以400×200的距离均匀分布110个控制点，以64×64的窗口大小，采用实相关、复相关、传统相位相关和本文改进的相位相关法进行配准（均基于分级配准策略），结果如表1所示。

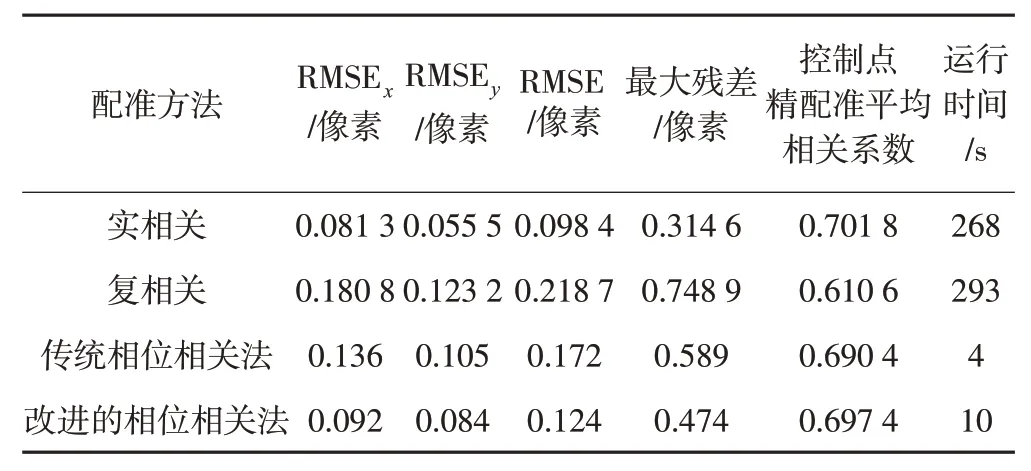
表1 不同方法的配准结果

相关配准的粗配准均采用卷积的FFT特性优化，精配准在粗配准周围-0.5～0.5个像素10倍过采样完成。剔除明显的误配准点，复相关配准得到的控制点最少（仅58），在相关性较低的地区往往失效，实相关和相位相关是基于实数的运算均得到102个控制点。由表1可知，当相关性较低时，实相关的精度和稳健性均高于复相关，实相关保留了大多数的控制点，而RMSE和残差依然较低；复相关剔除了较多控制点，RMSE和残差却较高，控制点的平均相关系数也有较大降低，这两种方法均涉及大量的重采样运算，导致计算量很大；传统相位相关法能有效提高效率；改进的相位相关法进一步提高了精度，其RMSE和平均相关系数很接近实相关，虽然计算量有所增加但仍远低于相关系数法。

3.2 窗口大小的影响

局部亚像素配准采用不同窗口大小时的配准结果如表2所示，可以看出，随着窗口大小的增加，精度有所提高，即使采取全局多项式拟合，在窗口大小为100时也可达到0.1像素的精度；但随着窗口大小的进一步增加，相关系数反而降低，这是由于配准窗口太大，窗口内像素偏移参数不一致导致的，且窗口大小的增加也带来了更大的计算量。

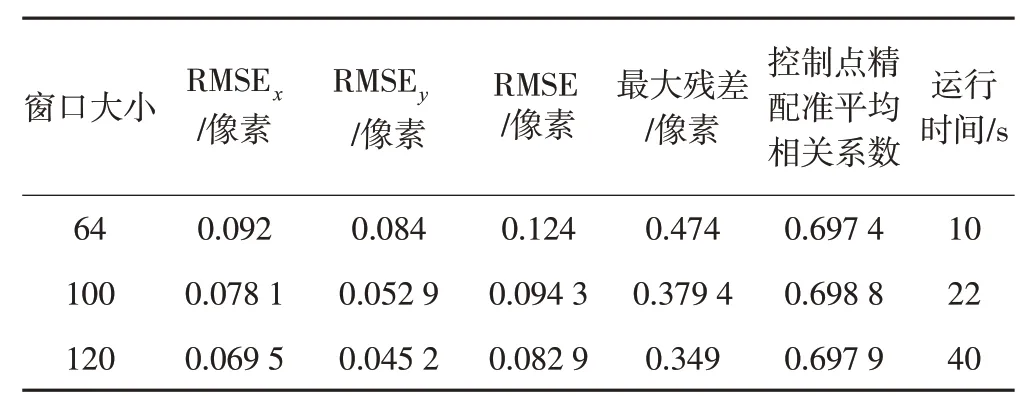
表2 不同窗口大小的配准结果

基于分级配准策略和改进的相位相关法，本文采用64×64的窗口进行配准，产生的干涉图如图4所示。

图4 配准干涉图

4 结语

对于SAR影像的高精度自动配准，大范围使用相位相关法忽略了影像内部位移的不一致性，亚像素配准中仍不可避免的存在大量小间隔的重采样操作，且传统相位相关法在亚像素偏移的求解过程中难以保证精度。本文以几何配准为初值，利用局部相位相关法可一步到位求取整像素位移量，通过多次曲线拟合迭代替代了传统的相位相关亚像素匹配法。该方法在保证精度和可靠性的前提下，避免了逐行逐点的搜索。实验结果表明，该方法在精度上十分接近实相关法，且能大大提高配准的效率。本文提出的方法对于旋转角较敏感，因此在进行相位相关时应对像对进行旋转纠正。对于两景畸变较大的影像或更加复杂的匹配情况，则需要与其他方法结合使用。