基于改进指数平滑神经网络模型的大坝沉降预测

2022-04-01韩宸宇李桂华

地理空间信息 2022年3期

韩宸宇，黄腾，李桂华，钱炜

（1.河海大学地球科学与工程学院，江苏南京 211100）

大坝在其服役过程中会承受恶劣环境的侵蚀、各种动静循环荷载作用，还会被各种突发性灾害影响，因此其局部结构和整体的安全性能将随时间的推移而逐步衰退。对于未完全自动化监测的长期服役大坝进行定期变形监测是确保大坝安全运营的重要保障，能更好地发挥大坝的重要作用[1-2]。沉降量是大坝变形监测工作中的重要指标之一，学者们针对大坝沉降监测如何选择更合适的模型达到较高的预报精度并顾及所用模型的鲁棒性、外延性等问题开展了深入研究，如谢海燕[3]等研究表明BP神经网络能对大坝数据进行拟合分析、预报研究；何自立[4]等构建了新维无偏灰色马尔可夫模型对大坝沉降数据进行预测，比传统无偏灰色模型精度更高；谢朋朋[5]等利用变权组合两种模型预测了大坝沉降变形，结果表明组合模型的预测精度比单一模型更高；刘造保[6]等采用改进平滑法处理了边坡的预测数据；贾强强[7]等提出的NMEA-BP模型解决了单一BP神经网络的缺点。上述研究中选用的数据量通常较多，采用的传统或改进的指数平滑法适用于小样本、随机性的数据序列，不适合长期预测，且往往难以有效描述沉降数据非线性的变化预测，预测误差仍需进一步有效控制；而BP神经网络能对数据的非线性部分进行深入处理，补足残差的影响。本文针对现有信息不足、样本小且呈非线性化的数据序列，构建了一种适用于长期预测的模型；并以某大坝沉降监测数据为例，运用改进的指数平滑BP神经网络组合模型进行了预测分析。

1 改进的指数平滑法

1.1 指数加权移动平均原理

指数平滑法是由霍尔特提出并经布朗发展而来的时间序列分析的重要分支之一[8]，广泛应用于金融数据分析等多个领域。在缺少相关的历史资料或事物发展趋势不明显、不稳定的条件下，采用这种方法进行短期预测具有一定的优越性[9]。该方法建立在移动平均法的基础上，认为历史数据对未来值的影响是随时间间隔的增长而逐渐减少的，同时使得预测值随实测值一样呈现一定的随机变动性。在整个预测过程中，不断利用预测误差来纠正新的预测值，即运用误差反馈原理不断修正预测值[6]。根据平滑次数的不同，指数平滑法可分为一次、二次和三次指数平滑法[8'10]。

将观测的沉降数据按时间序列记为y1、y2、…、yt，设α为静态平滑常数(0≤α≤1)，t时刻一次平滑值由当前观测值yt和上一时刻平滑值分别乘以系数α和1-α所得，也可视为t-1时刻的平滑值加上平滑常数α乘以下一时刻观测值与t-1时刻的平滑值之差，即

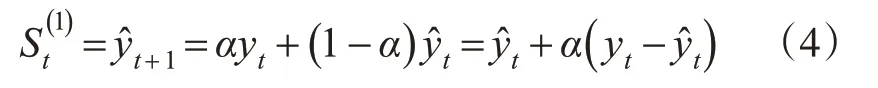
一次指数平滑法能较好地拟合小范围波动较平稳的数据序列，二、三次指数平滑法是在一次指数平滑法的基础上重复平滑过程，二次指数平滑法适合拟合呈直线趋势的序列，三次指数平滑法适合拟合呈二次曲线趋势的序列，在t时刻它们的平滑值的计算公式为：

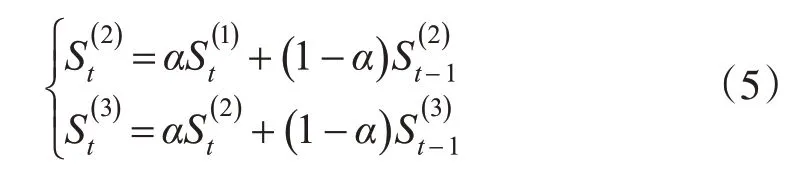
二次指数平滑法进行预测的模型可表示为[11]：

式中，m为预测值与t时刻观测值的间隔数。

三次指数平滑法进行预测的模型可表示为：

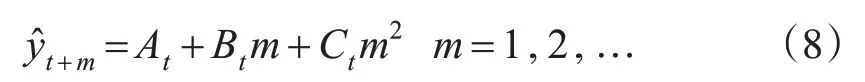
将式（8）的系数展开可表示为[11]：

1.2 改进的指数平滑预测

在实际应用中，α的取值较为关键，通常根据经验和试算结果在0～1范围内确定α的大小。该方法的优势在于当预测结果较好时容易得出数据的内部规律，但出于沉降数据序列复杂变化性和能及时跟踪变化达到长期预测目的的考虑，需对α和预测流程进行一定的优化。本文将平滑后的绝对误差平方和达到最小作为控制的目标函数[12]，即

α的取值范围是固定的，从零开始对于每个α可遍历计算得到所有的绝对误差平方和，取使绝对误差平方和最小的α为最优平滑常数进行最终的预测。遍历α时可选择小的步长来提高精度，本文采用3种平滑方法对一定量的实测数据进行实验发现，步长为0.1、0.01、0.001和0.000 1时，运算时间无显著差别，但对精度提高的能力却迅速下降，并无必要采用0.000 1的步长。对于适合工程数据的步长0.01和0.001，本文选择0.001作为应用的步长。根据相关文献，本文在预测方法流程上提炼了两种改进思路。

1）全局最优平滑法。该方法利用平滑法将已知的沉降数据全部纳入样本范围进行预测[6]，结合上述内容，其计算过程为：①选定适合的平滑预测方法，确定初始值S0，令α=0；②计算各期沉降数据相应的平滑值以及平滑值与沉降数据的绝对误差平方和并存储；③令α增加0.001，重复步骤②，直至α=1结束，搜索误差平方和数组中最小值所对应的α；④计算最终α对应的预测值。这样找到的最优平滑常数α，显然比简略的试算法更好，但这样确定α的平滑预测模型仍属于静态模型范围，需要改进模型来增加对长期观测数据的适应性。较简便的方法是每增加一个新的观测数据，就重复一次上述流程，使得α不断变化，增强了模型的适应性。

2）局部最优平滑法。该方法将α修改为时间的函数并提高参与数据的流动性[13]，前者与使用同样参数的传统平滑模型相比改进效果有限，后者是为了更好地跟踪数据变化，具体流程为：①选择一段沉降数据作为处理序列，对于N期沉降数据（开始为1～N期）选定适合的平滑预测方法，确定初始值S0，令α=0；②计算各期沉降数据相应的平滑值及其与沉降数据的绝对误差平方和并存储；③令α增加0.001，重复步骤②，直至α=1结束，搜索误差平方和数组中最小值对应的α；④计算最终α对应的预测值并存储；⑤剔去所选N期沉降数据中第一期，补入N+1期对应的观测值，重复步骤②～④。

由于待预测数据的未知性，在进行数据预测时，可将全局最优和局部最优的预测结果取平均来降低较坏预测情况的可能性。无论是全局最优还是局部最优，从后验的角度可能其中某一模型预测效果更好，但对于与当前时刻数据有较强或较弱联系的待测数据，都会有一半概率产生更大的偏差。本文将二者结合起来，简称为综合平滑法，使得产生更大偏差的概率降为1/4，同时提高了单一改进的长期适应性和鲁棒性。

2 改进指数平滑BP神经网络组合模型

2.1 BP神经网络

BP神经网络是一种多层前馈神经网络，结构如图1所示，主要由输入层、隐含层和输出层组成，各层之间利用神经元由传递函数（激活函数）连接。信号向前传递到输出层后，利用梯度下降法计算目标函数结果，然后误差信号反向传播，循环往复调整输入层和隐含层的权值与阈值，当训练后误差达到期望范围或进一步的训练不能降低误差时可停止网络的训练。

图1 BP神经网络结构

2.2 组合模型

为了达到更好的预测效果，可尝试利用BP神经网络对非线性化的残差部分进行进一步处理。改进指数平滑神经BP神经网络组合模型将综合平滑法和BP神经网络有机结合起来，具体流程为：

1）利用综合平滑法对记为Yt=[y1,y2,…,yt]的一组观测数据进行处理，得到平滑后的值St=[S1,S2,…,St]，则Yt可表示为：

式中，et=[e1,e2,…,et]为综合平滑法的残差。

2）输入端神经元的样本数据为et-1,et-2,…,et-N,St，N为局部最优平滑法采用的期数；输出端神经元的数据为et，得到训练好的BP神经网络。

3）训练完成的网络将St及其相应的残差序列et-1,et-2,…,et-N作为输入的预测样本，得到输出的预测残差êt，最终的预测值为：

3 工程实例分析

为验证改进指数平滑BP神经网络组合模型的适用性，本文选取某大坝监测点共16期的沉降数据进行建模分析预测，如表1所示，前14期数据为已知数据建模，后两期数据用于验证分析。

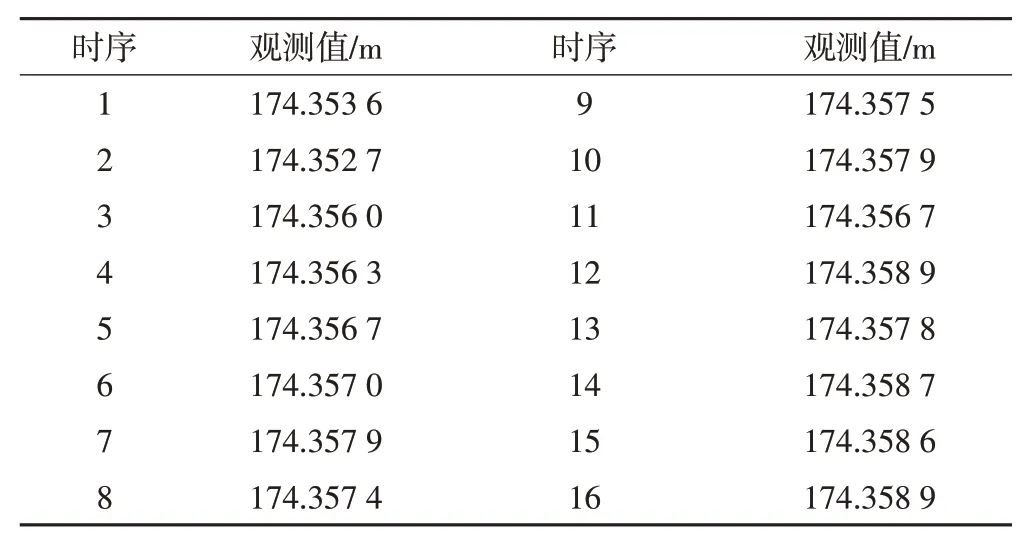
表1 已知观测数据样本

本文根据数据的波动特性，尝试分别采用一次和三次指数平滑法进行预测。通过1～14期的数据预测第15期的沉降量，再将第15期沉降量的预测值添加到已知数据序列预测第16期的沉降量。在一次指数平滑时，将前两期沉降数据的均值作为初始值，分别利用一次全局最优平滑法和一次局部最优平滑法（取N=4）处理得到第15、16期的一次综合平滑预测值。在三次指数平滑时，将前3期的沉降数据作为初始值，分别利用三次全局最优平滑法和三次局部最优平滑法（取N=4）处理得到第15、16期的三次综合平滑预测值。上述结果简化后如表2所示。

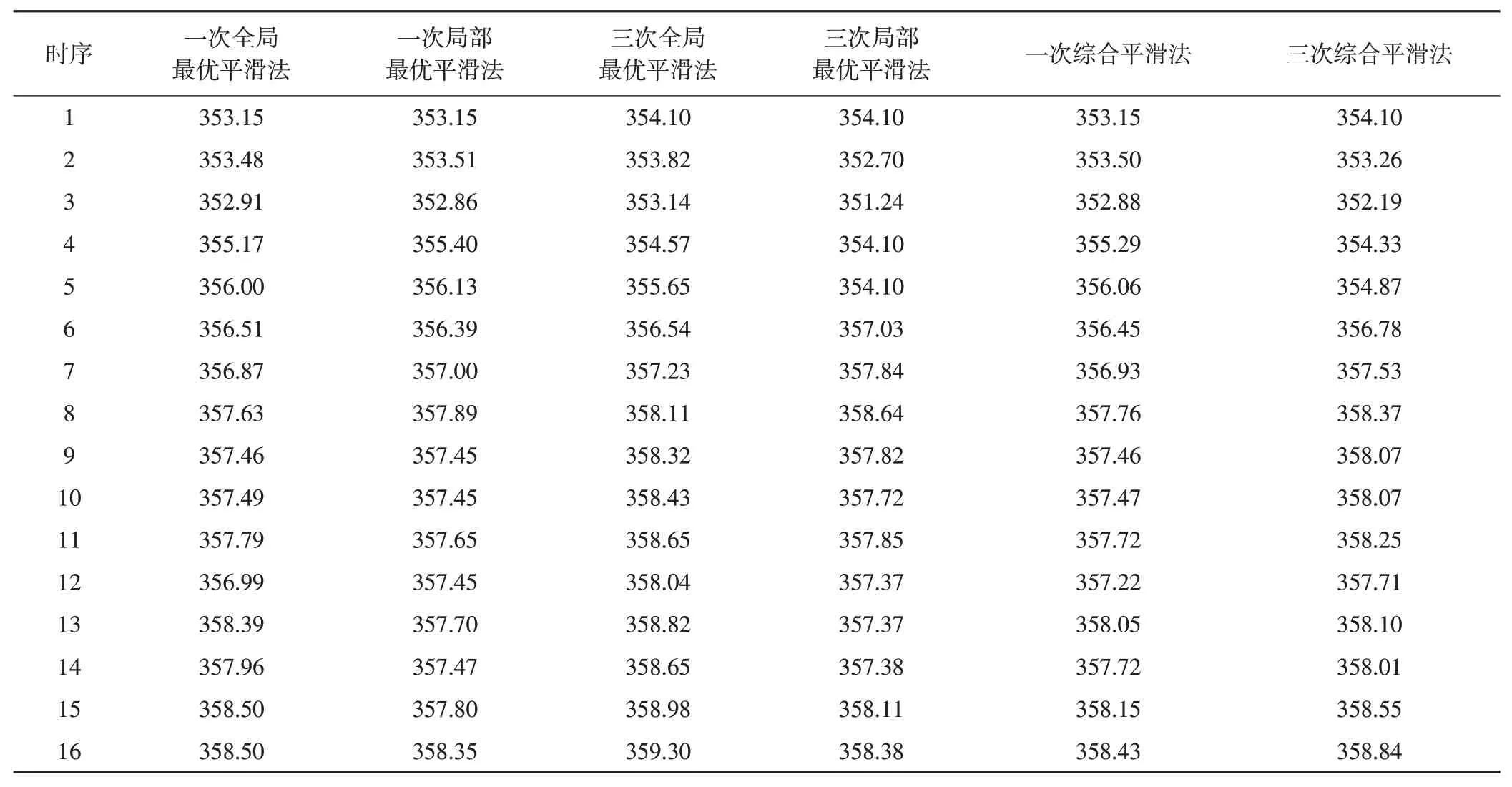
表2 各类平滑方法的平滑预测值/mm

对残差进行BP神经网络处理时，同样取N=4，在建立的单隐含层网络中，输入端的神经元个数为5，训练目标为0.001，最大训练次数为1 000；经过一定尝试设置隐含层节点数为8，获得相应的预测结果，并与灰色GM（1'1）模型和其他模型进行了比较。利用预测结果的绝对误差进行精度分析，由表3可知，涉及指数平滑的模型总体效果均优于灰色模型，其中传统的三次平滑法比一次平滑法效果好，使得三次综合平滑法比一次综合平滑法的预测效果好，综合指数平滑模型的精度比传统指数平滑模型略有提高。残差处理后的改进一次指数平滑BP神经网络组合模型最终的最大绝对误差为0.177 mm，约为灰色预测模型的1/4，与传统一次平滑法相比预测精度有较大提高。改进三次指数平滑BP神经网络组合模型的最大绝对误差值仅-0.022 mm，与其他模型相比，预测效果有明显提高。