水荷载在弧形闸门各主要受力部件间的分配和传递

曹慧颖 马仁超 余俊阳

摘要：弧形闸门是各构件协调工作的空间结构体，水压荷载在闸门各构件之间如何分配和传递目前尚不完全清楚，只有弄清楚闸门各构件承受的荷载，其结构计算的成果才会精确。以小湾水电站泄洪洞的弧形工作门为例，采用有限元内力法确定水压荷载作用下闸门各主要受力部件的相互作用力，并根据其计算成果求解出各构件的内力，与现行规范中平面体系法计算结果进行对比，指出了平面体系法的不足之处。同时，由于有限元内力法是建立在有限元法的基础之上的，不但具有有限元法的优点，而且该方法还可以消除闸门某些部位不合理的应力集中的影响，计算出的结果更为合理。相关成果可供类似工程闸门受力计算参考。

关 键 词：荷载分配; 弧形闸门; 有限元内力法; 结构内力计算; 小湾水电站

中图法分类号： TV663   文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.01.025

0 引 言

对于大型弧形钢闸门，其主要特点是构件的刚度较大，结构的节点效应和空间效应很强。现行闸门设计规范的平面体系算法过于简单，计算假定已不符合实际情况，不能真实反映大型弧门这样一个空间结构的工作性态及其复杂的受力条件[1]，计算结果的误差较大，已不能满足大型弧门的安全要求[2]。因此，以空间结构的观点建立弧形闸门计算模型，采用三维有限元分析研究閘门各部件的受力情况，是确保闸门安全、经济、合理的重要前提条件。

三维有限元法是采用三维建模和分析计算，能够真实地反映闸门各部件之间的受力传递关系，但是由于局部网格的角缘现象，导致个别部位应力集中，不能准确求解闸门各局部构件的应力。有限元内力法的计算原理是[3]：由三维有限元法计算得到节点位移和单元刚度矩阵，据此直接求得结构各主要剖面网格结点上的有限元内力值，然后根据截面的几何形状直接等效为结构的内力[4]。因此，可以通过有限元内力法确定出闸门各构件的受力和内力分布情况，然后通过材料力学法求解各构件的应力，这样可以克服有限元计算中网格质量对结构应力的影响，避免局部的应力集中。

弧形闸门是各构件协调工作的空间结构体系，精确地把作用在闸门上的水压荷载分配到闸门各构件上是一个复杂的课题。但是，弄清水压荷载在闸门各受力构件间的分配和传递关系，是进行结构受力简化计算的前提。因此，采用有限元内力法确定闸门各部件间的相互作用力，弄清水压荷载在闸门各受力构件间的分配和传递关系，并根据其计算成果求解各构件的内力，具有较大意义。

1 工程概况

小湾水电站是澜沧江中下游规划建设的8座梯级电站中的第二级，是澜沧江中、下游河段的龙头水库和巨型电站。电站装机容量4 200 MW，总库容151.32亿m3。水库最高水位1 242.51 m，正常蓄水位1 240.00 m。电站泄洪系统由坝身表孔、坝身中孔和左岸泄洪洞组成，泄洪洞进口设平面事故闸门，中段设弧形工作闸门。

泄洪洞弧形工作闸门具有表孔闸门的孔口尺寸、深孔闸门的设计水头，闸门孔口宽度13.0 m，孔口高度13.5 m，底槛高程1 194.135 m，设计水头46.0 m。闸门操作条件为动水启闭，有局部开启要求。小湾水电站规模大，且泄洪洞承担水库20%的洪水宣泄，其工作闸门的重要性不言而喻。

泄洪洞弧形工作闸门采用双主横梁、直支臂结构，门叶结构采用主横梁同层布置，面板支承在水平次梁、竖直次梁及主横梁构成的梁格上。弧形闸门半径23.0 m，支铰高度19.0 m。闸门支承型式为圆柱铰支承。闸门材料为低合金高强度结构钢Q345B。

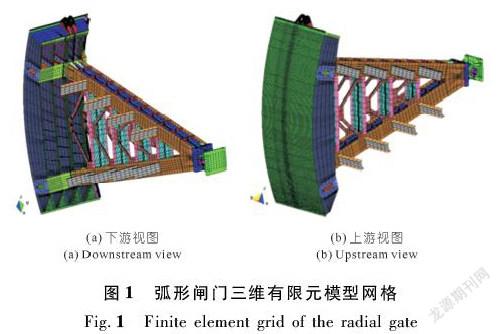
2 弧形闸门三维有限元模型

2.1 单元类型选取及网格划分

小湾水电站泄洪洞弧形工作闸门为一对称结构（见图1）。作用在闸门上的水压荷载为梯形荷载，闸门结构和作用在闸门上的荷载均关于闸门中心线对称，故可取闸门的一半进行研究[5]。取闸门结构的半边建立三维有限元模型，采用的单元型式包括八节点等参单元、四边形板单元和两节点杆单元，这里的四边形板单元是指卜小明等[6]提出的任意四边形板单元，该单元与常规矩形板单元不同，应力分量包含面内应力分量和弯曲应力分量。

闸门固定支铰、活动支铰及支铰轴为实体结构，采用空间八节点等参单元模拟;闸门面板、水平次梁（见图2）、竖直次梁、主横梁、支臂以及连接部位的加强板为板壳结构，采用四边形板单元模拟;闸门底止水采用两节点杆单元模拟。有限元计算模型节点数为39 735个，单元数为43 815个，其中八节点等参单元2 498个，四边形板单元41 250个，两节点杆单元67个。

计算坐标系选取X轴正向为顺水流方向，Y轴正向为垂直于水流指向左岸方向，Z轴正向为竖直向上，闸门支铰中心为坐标原点。

2.2 约束的处理

计算模型中，弧形闸门对称面上施加对称约束，以限制其绕X轴、Z轴的转动和Y向平动;闸门固定支铰底板处施加固定约束，以模拟固定支铰与混凝土的接触;闸门底部施加沿面板环向的约束，以模拟闸门底部与底槛混凝土的接触。同时，在实体单元和板单元连接处、杆单元和板单元连接处考虑位移协调。为了模拟支铰在闸门运行过程中的转动效果，在固定支铰、活动支铰与支铰轴连接处设置接触面单元，按三维非线性无摩擦接触问题来考虑[7]，即在支铰轴与固定支铰、活动支铰接触处，铰轴只传递法向压力，不传递法向拉力及切向力。

3 荷载分配及内力计算

3.1 闸门各构件受力分析

基于以上三维有限元模型，采用有限元内力法对小湾泄洪洞弧形工作门各主要构件的受力情况进行计算，确定各构件的相互作用力。经计算，闸门各构件节点上可得到X、Y、Z 3个方向的力和力偶共6个分量，其中力偶相对力来说对构件的影响较小，这里不予考虑。由闸门的变形分析可知，闸门面板及其他构件沿径向的变形较大，Y向的变形相对小得多，这里只给出了将X、Z向节点力投影到闸门径向得到的节点力分布。

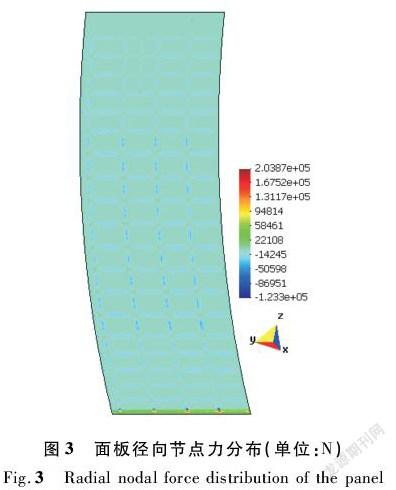
闸门挡水时，面板首先将水压荷载传递到直接与之相连的水平次梁和竖直次梁，同时也受到水平次梁和竖直次梁的反作用。图3是面板的径向节点力分布图，从图中可以看出，在与水平次梁、竖直次梁连接部位，面板的受力均为负值。

图4是将水平次梁X和Z向节点力投影到闸门径向（即水平次梁横向）得到的节点力分布图，从图中可以看出：水平次梁与面板的连接部位承受面板传来的水压荷载，与竖直次梁的连接部位承受竖直次梁的约束反力。水平次梁最大正向力（正向为闸门径向指向闸门支铰的方向，下同）发生在水平次梁9上游侧靠近边梁的跨段，最大负向力（负向为闸门径向逆向闸门支铰的方向，下同）发生在水平次梁9与竖直次梁5的连接部位。竖直次梁对水平次梁4～13的约束反力具有如下特征：竖直次梁3和竖直次梁5对水平次梁的反力比其他竖直次梁大，竖直次梁5最大。

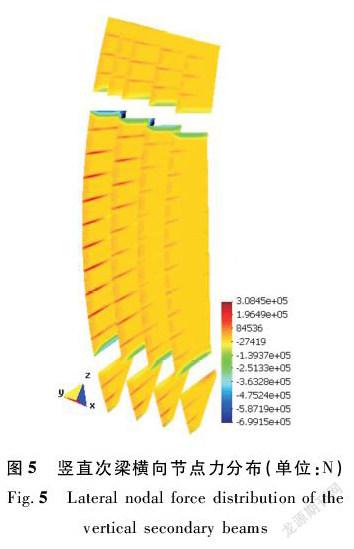
图5是将竖直次梁X和Z向节点力投影到闸门径向（即竖直次梁横向）得到的节点力分布图。从图中可以看出：竖直次梁与水平次梁的连接部位承受水平次梁传来的集中荷载，与面板的连接部位承受面板传来的分布荷载，与主横梁的连接部位承受主横梁的约束反力。竖直次梁最大正向力发生在竖直次梁5上游侧跨中部位，最大负向力发生在竖直次梁5与主横梁的连接部位。竖直次梁3和5承担的荷载明显大于竖直次梁1和2，竖直次梁5最大。这是因为竖直次梁3和5与支臂直接连接，与主横梁同高，相当于纵向主梁的作用，承担的水压荷载较大，同时竖直次梁5在竖直次梁3的外侧，因此承受的荷载更大一些。

图6～8是将主横梁腹板、前翼缘、后翼缘的X和Z向节点力投影到闸门径向（即主横梁横向）得到的节点力分布图。从图中可以看出：主横梁与竖直次梁的连接部位承受竖直次梁传来的集中荷载，与面板的连接部位承受面板传来的分布荷载，与支臂的连接部位承受支臂的约束反力。主横梁上的最大正向力发生在上主横梁下侧腹板与竖直次梁5的连接处，最大负向力发生在上主横梁下侧腹板与支臂的连接部位。在竖直次梁与主横梁的连接处，主横梁承受的荷载明显大于其他部位，面板直接传给主横梁的荷载与竖直次梁传给主横梁的荷载相比微乎其微。

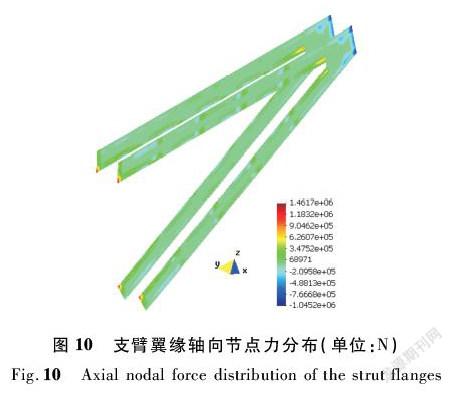
图9～10是将支臂腹板和翼缘的X和Z向节点力投影到闸门径向（即支臂轴向）得到的节点力分布图。从图中可以看出：支臂与主横梁的连接部位承受主横梁传来的荷载，与支铰的连接部位承受支铰的约束反力。支臂上的最大正向力发生在上支臂下侧腹板与主横梁连接处，最大负向力发生在上支臂下侧腹板与支臂连接处。因顶梁至上主横梁的距离大于底梁至下主横梁的距离，故上主框架承担的水压荷载比下主框架要大。

3.2 閘门各构件内力计算

根据上节计算出的闸门各构件节点力，采用结构力学中的截面法即可求到构件上各截面的内力。水平次梁的最大弯矩和剪力均发生在水平次梁9的支座B处，弯矩为542 930 N·m，剪力为560 927 N。竖直次梁的最大弯矩基本发生在跨中处，最大剪力发生在支座A处，梁5的内力在各竖直次梁中最大，弯矩值为6 794 117 N·m，剪力为4 305 831 N。主框架的最大弯矩发生在主横梁跨中，最大剪力发生在主横梁与支臂连接处，上主框架的内力比下主框架的大，弯矩为8 136 233 N·m，剪力为5 585 657 N。

4 有限元内力法与平面体系法的荷载分配与内力成果对比4.1 荷载分配计算结果比较

表1给出了有限元内力法和平面体系法下各水平次梁承受的荷载值。从表中可以看出：平面体系法比有限元内力法求解出的水平次梁承受的总荷载值要大，这是因为平面体系法中水平次梁的荷载分配按“相邻间距和之半法”进行，这样会把本应是竖直次梁承受的荷载当作是水平次梁承受来计算，得出的水平次梁承受的荷载自然就会偏大;平面体系法下，水平次梁单位宽度承受的荷载随水头的增加而增大，基本上呈线性变化。而有限元内力法下，水平次梁单位宽度承受的荷载随水头的增加并不是简单的线性变化，这是因为弧形闸门与平板闸门不同，水平次梁承担的荷载会受到面板曲率变化的影响。

在水平次梁与竖直次梁、边梁的连接处，水平次梁除承受面板传来的水压荷载外，还受到竖直次梁及边梁的约束反力，将该处水平次梁承受的合力除以各竖直次梁、边梁的控制长度，分析各竖直次梁、边梁对水平次梁的约束反力。

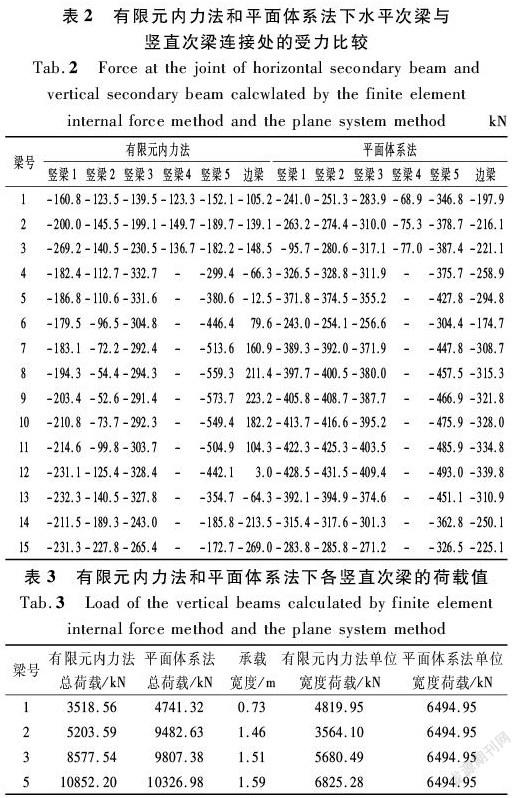
表2对有限元内力法和平面体系法下水平次梁与竖直次梁、边梁连接处的受力情况进行了比较，表中负值代表力的方向与水压荷载方向相反。从表2可以看出：有限元内力法下，在水平次梁与竖直次梁3、5连接处，水平次梁上的作用力比其他处要大，说明竖直次梁3、5对水平次梁的约束反力比其他次梁要大，这是因为这两根次梁与支臂相连，比其他竖直次梁刚度要大，承受的水压荷载较多。在水平次梁6～12与边梁的连接处，水平次梁上受到与水压荷载相同的作用力，这说明该处水平次梁没有受到边梁的约束反力，也就是说，由于边梁的刚度较小（高度仅为其他竖直次梁的25%），没能起到水平次梁的端支承作用，反而使水平次梁成为它的中间支承;然而，平面体系法下水平次梁上的作用力相差较小，说明边梁和各竖直次梁对水平次梁的约束作用差别不大。综上可知，平面体系法计算时没有考虑各梁系的相互联系和变形协调关系，而有限元法计算时能够考虑闸门整体的相互协调性。

因此，对于大型弧形闸门，边梁和水平次梁不能盲目按平面体系法设计，必须通过边梁与水平次梁的变形协调计算，使边梁除有足够的强度外还应有足够大的刚度。否则实际上梁系的传力方式将从常规设计的“水平次梁-边梁-主横梁”部分变成“边梁-水平次梁-竖直次梁”，设计计算结果将严重失真。

表3给出了有限元内力法和平面体系法下各竖直次梁承受的荷载值。从表中可以看出：对于竖直次梁1和2承受的总荷载值，平面体系法比有限元内力法求解出的结果要大，而与支臂直接相连的竖直次梁3和5承受的总荷载求解出的结果相差并不大。平面体系法下，各竖直次梁单位宽度承受的荷载相同;有限元内力法下，与支臂直接相连的竖直次梁3和5承担的荷载大于其他次梁。

表4给出了有限元内力法和平面体系法下闸门主框架承受的荷载值。从表中可以看出：有限元内力法下，上、下主横梁与纵向主梁（即竖直次梁3和5）一起承担闸门上的水压荷载，由于顶梁至上主横梁的距离大于底梁至下主横梁的距离，上主横梁承担的水压荷载大于下主横梁所承受的;主横梁式框架结构算法下，每个主横梁框架上分配到的荷载相等，各承担1/2的水压荷载。

4.2 内力计算结果比较

表5给出了有限元内力法和平面体系法下水平次梁的最大内力值。从表中可以看出：虽然前述有限元内力法计算出的各水平次梁承受的水压荷载比平面体系法小，但是该方法得出的次梁内力比平面体系法大得多。这是由于平面体系法把竖直次梁和边梁作为刚性支座，计算对水平次梁的约束反力，而其实边梁的刚度远小于竖直次梁的刚度，边梁处的变形较大，在水平次梁6～12與边梁的连接处，边梁不但没能起到支承作用，反而使水平次梁成为它的支承。

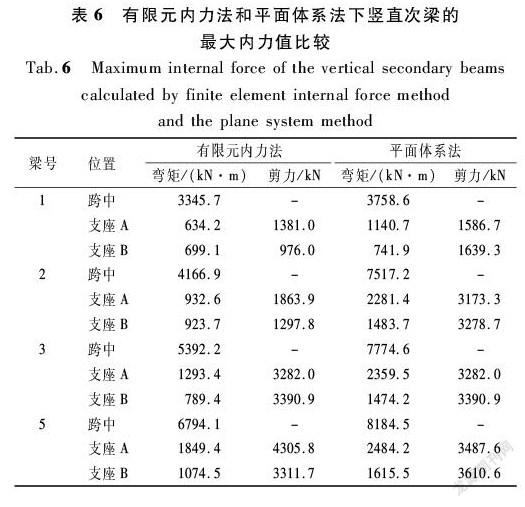
对竖直次梁而言，最大弯矩发生在跨中处，最大剪力发生在支座处。表6给出了有限元内力法和平面体系法下竖直次梁跨中和支座处的内力值。从表中可以看出：平面体系法得到的内力值比有限元内力法得到的要大。虽然两种方法求解出的竖直次梁3和5承受的总荷载相差不大，但是由于竖直次梁3和5除了受到上、下主横梁两个作用较大的支承外，还受到支臂竖向连接系和底梁的支承，有限元内力法考虑了这些因素，而平面体系法只是把竖直次梁看作支承在主横梁上的双悬臂梁进行计算，没有考虑上述因素。

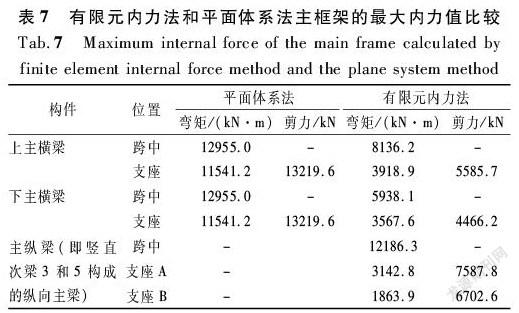
表7给出了有限元内力法和平面体系法下主框架跨中和支座处的内力值。从表中可以看出：采用平面体系法求解出的主横梁跨中处的弯矩值比有限元内力法的结果大得多，这是因为平面体系法认为上、下主横梁承受全部的水压力，而实际上，竖直次梁3和竖直次梁5因直接与支臂连接，其荷载并没有通过主横梁传递，而是直接传给了支臂。

5 结 论

（1） 本文采用三维有限元内力法确定水压荷载作用下弧形闸门各主要受力部件的相互作用力，并根据其计算成果求解出各构件的内力，能够较好地体现出闸门的空间效应和闸门各构件的受力情况。

（2） 平面体系法中，水平次梁的荷载分配按“相邻间距和之半法”进行，竖直次梁承担的荷载为所控制区域的水压力形成的梯形荷载。由于水平次梁与竖直次梁的控制区域有交叉重合的部分，此处荷载被重复计入。有限元内力法中，次梁每个节点上承受的荷载都可以精确得到，更能反映出次梁实际的受力情况。

（3） 对于大型弧形闸门，边梁和水平次梁不能盲目按平面体系法计算，必须通过边梁与水平次梁的变形协调计算，明确水平次梁和边梁的传力方式后，才能进行次梁的内力和应力计算。

（4） 平面体系法中，上、下主横梁框架承受全部的水压力，而实际上闸门上的水压力由主横梁和纵向主梁一起承担。但在有限元内力法中，上、下主框架上每个节点上承受的荷载都可以精确计算出，更能反映主框架实际的受力情况。

参考文献：

[1] 曾又林，何文娟，李亚菲.高坝洲深孔弧门三维有限元分析[J].湖北水力发电，2002（1）：13-15.

[2] 朱芳，段克让，曹以南.漫湾弧形闸门有限元应力分析[J].水力发电学报，1993（4）：22-32.

[3] 李同春，温召旺.拱坝应力分析中的有限元内力法[J].水力发电学报，2002（4）：18-24.

[4] 颜天佑，李同春，赵兰浩，等.有限元法求解截面内力方法比较[J].水电能源科学，2008（3）：141-143.

[5] 龙驭球，包世华.结构力学教程[M].北京：高等教育出版社，2000.

[6] 卜小明，龙驭球.一种薄板弯曲问题的四边形位移单元[J].力学学报，1991，23（1）：53-60.

[7] 郑克红.高水头弧形钢闸门三维有限元分析[D].南京：河海大学，2005.

（编辑：胡旭东）