基于NMI特征的遥感影像线性迭代聚类超像素分割算法
2022-03-31李静
李 静
(北京跟踪与通信技术研究所,北京100094)
1 引 言
随着对地观测技术的不断进步,人们对地球资源和环境的认识不断地加深,遥感图像的分辨率也不断提高,逐渐地展现出结构、形状、纹理等细节信息,拉动了人们对高分辨率遥感影像的应用需求。然而高分辨率遥感图像所包含的大量细节信息无疑会给现有的图像应用算法带来巨大的负担。因此,国内外学者从各角度提出许多能够减轻图像应用算法繁重计算量的图像预处理方法,其中就包括图像分割。
遥感图像超像素分割是将一幅遥感影像的像素根据空间位置关系、颜色等各属性进行分类,最后将各类像素组合成若干个具有同质性的对象,即为超像素。超像素遵循空间上的连续且互斥的特性,其分割质量直接决定了后续图像处理的有效性。传统的基于像元的图像分割方法只关注遥感图像的光谱信息,未考虑纹理细节等因素的干扰,导致分割后的图像像元之间相关性差,分割结果具有很大的不确定性,再加上图像固有噪声的影响使得图像分割后的影像存在“椒盐”效应,分割后的图像缺乏连贯性[1-2],给后续的图像应用带来局限性。因此提出一种能够结合并利用纹理信息、具备噪声鲁棒性的图像分割技术成为迫切需要。
为了充分展示图像像素特征的空间分布关系,许多学者提出了超像素分割算法[3-4]。该类分割算法是按照某种相似度准则,将图像划分为接近均匀并互斥的图像块。这些算法虽然各有差异,有着不同的优缺点,但都采用了聚类的基本思想,大都提高了后续图像处理的运算速度[5-9]。简单线性迭代聚类(Simple Linear Iterative Clustering,SLIC)算法是一种简单高效的超像素分割算法,使用减小搜索范围的K-means聚类算法高效地组成超像素[5]。而且相比较其他超像素分割算法,SLIC算法原理简单,占用内存少、运算快,能够得到较为紧凑和均匀的超像素,具有良好的边缘贴合度,使其在图像分割领域得到了广泛应用。
但将SLIC超像素算法直接应用到遥感图像分割领域时,由于遥感影像较一般图像复杂得多,会有更多细小的特征和纹理,导致分割结果中会存在过分割的现象,算法分割性能较差。近年来,国内外研究者提出了许多改进方法。刘仲民等人首先用SLIC超像素算法获得初始分割结果,接着利用区域邻接图和最近邻接图的邻接表数据结构来表示区域之间的关系,然后计算每个待合并区域与其所有邻接区域之间的相似度函数值,最后根据该值合并相似度值较小的区域,得到最后的分割结果[10]。该方法减轻了由遥感图像固有的噪声引起的分割图像不连续的现象,但其合并的方法额外地增加了计算复杂度。文献[11]将灰度共生矩阵提取的影像纹理特征与SLIC获得的颜色特征相结合,并扩展了衡量加权纹理距离和颜色相似度以及超像素中心与相邻像素之间的空间接近度的度量方法,充分考虑了纹理特征,减轻由纹理导致的过分割现象,但未解决由噪声引起的分割后图像的不连贯现象。
本文针对上述问题在现有SLIC算法的基础上进行改进:首先针对遥感影像的椒盐噪声,采用引导滤波器对其进行平滑;然后利用现有的SLIC算法初步确定超像素,进而判断出微小超像素块,对相邻超像素块根据归一化转动惯量信息计算超像素的相似性度量值,根据相似性度量将较小超像素吸收合并。与文献[10]提出的合并方法相比,本文提出的合并方法具有较低的计算复杂度,此外,本方法避免分割出微小超像素块,有助于加速后续的遥感图像处理过程。
2 引导滤波
传统SLIC分割方法直接对原图进行分割,容易受到噪声点的影响,致使分割后的图像缺乏连贯性。一般的各向同性滤波(例如简单平滑或高斯平滑)无法区分噪声和边缘,于是对二者进行统一处理,导致在噪声被磨平的同时,也模糊了图像中的边缘、纹理等重要的细节信息。目前各种针对高斯滤波去噪算法的改进关键点是对标准差和滤波尺度的最优化选取问题,本质上还是各向同性滤波。为了克服上述问题,本文采用引导滤波器滤除噪声。
引导滤波的优势在于它能够利用引导图像中的边缘结构信息,避免平滑过程对边缘结构造成破坏。它是一个线性的滤波过程,包括引导图像I,输入待滤波图像pj和输出图像qi。引导图像I和带滤波图像pj需要根据具体应用事先设定,其中I也可以直接取为输入图像pj,图像引导滤波器输出图像中的第i个像素可以表达为一个加权平均值[12]:

其中:i和j为图像像元位置;滤波核W ij是引导图像I的函数,并与p j无关。
图像引导滤波器假设滤波器是关于参考图像I和输出图像q的一个局部线性变换模型。即假设在以像素k为中心的一个图像窗口w k内,输出图像qi是参考图像I的一个线性变换[12]:

其中:线性系数ak和bk在窗口w k中为常数,可通过最小化窗口w k中的代价函数来求解ak和bk:

其中:μk和σ2k是引导图像在窗口w k内的局部均值和局部方差,ε是一个用于防止ak过大的正则参数,|w k|为窗口内的像素个数。
在计算完所有窗口内的线性系数后,文献[12]给出引导滤波器的核函数权值W ij可用下式表达:

3 改进的SLIC超像素分割算法
3.1 SLIC算法
Achanta等人利用SLIC算法生成均匀且紧凑的超像素,与地物边界贴合效果较好,分割效果也符合人们的期望。该算法是一种基于Kmeans聚类梯度下降的超像素分割算法,分割后的超像素由聚类中心和附属像素组成。该算法首先在图像中随机但近似均匀地分布K个种子点,然后根据各种子点对应像素的CIE-Lab空间色彩值L,a,b以及像素点在影像中的位置(x,y)组成五维特征向量[L,a,b,x,y]T,其中,L表示亮度,a表示从绿色到红色的分量,b表示从蓝色到黄色的分量。SLIC采用CIE-Lab作为颜色空间,是由于它较RGB更符合人眼主观感受。根据这五维特征向量构造距离度量标准,将图像中每个像素与K个种子点的相似度聚类,分割成K个完全分割且互斥的局部区域,称之为超像素。具体步骤如下:
3.1.1 初始化聚类中心
首先根据需要设定预期的超像素数量K,为了获得形状规则均匀的超像素,需要将K个种子点均匀分布,假设图像有N个像元,则相邻两个
3.1.2 相似度计算
SLIC算法的类内相似度度量包括颜色距离和空间距离,度量方法可表示为:
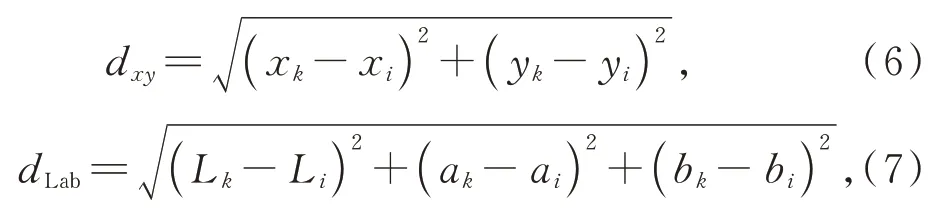

其中:d xy为空间距离;dLab为颜色距离;D'为像素点i与种子点k之间的距离为类内最大距离;N C为最大的颜色距离,随图像、聚类的不同而不同,可用固定常数n表示,取值范围为[1,40];从公式中可以看出,n可用来控制相似度公式中颜色差异和空间距离的比例,一般取10;D为最终的度量距离。
3.1.3 迭代优化聚类中心
与标准的K-means聚类算法在全局搜索不同,SLIC算法以每个种子点的2S×2S范围为每个像素计算与其邻近的种子点的距离,大大减少了运算量。然后确定与其距离最小的种子点,最后确定分配类标签,然后将属于同一个聚类中心像素点的五维向量平均后得到新的聚类中心,不断迭代使误差收敛,一般需要迭代10次。计算均值的方法可表示为:

其中:φj为超像素j中所有像素的均值,N'为超像素中的像素个数,Gj为超像素j的区域。
3.2 基于NMI特征的超像素合并
由前面的步骤可以看出,当K值较大时,分割结果中会出现明显的过分割现象。针对过分割产生的微小超像素块,还需合并到临近的超像素块中。针对具有多个领域的微小超像素块,本文采用图像绕质心的归一化转动惯量(Normalized Moment of Inertia,NMI)度量其与多个邻域超像素块的相似性度量。
SLIC算法的类内相似度度量仅仅利用了图像颜色和空间的距离。对于颜色纹理相似的区域,如果能考虑单个区域的整体特征,将有助于提高超像素块的分割精度。NMI特征是图像的二阶矩特征,它利用图像的空间信息反映了图像颜色空间分布的复杂程度,具有伸缩、平移和旋转不变性等特点,作为一个有效的特征已被应用于图像匹配中[12]。在本文中,该特征作为超像素块间的相似量度。对于一幅M×N的数字图像,每个像素都可以被看作是Oxy平面上的质点,其灰度值I(i,j)可看作是相应质点的质量,结合物理学相关概念,对图像作如下定义:二维灰度图像所有的灰度值之和为该灰度图像的质量,记为m,则有[13]:

图像质心,记为(i0,j0),则有:
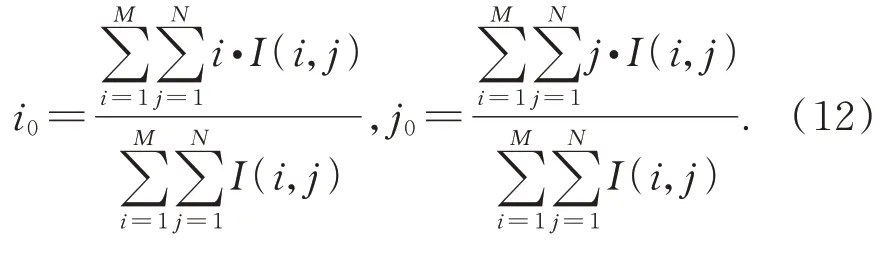
若二维图像的灰度值分布均匀,其质心同时也就是该图像所占平面图形的形心。若将图像绕其质心(i0,j0)的转动惯量记为J(i0,j0),可定义如下:
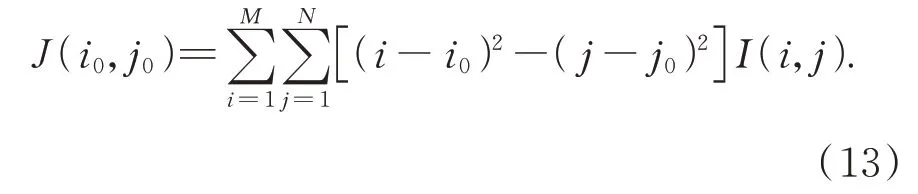
根据图像质量、质心、转动惯量的定义,给出图像绕质心的归一化转动惯量,简称归一化转动惯量:

该式表明,绕质心的归一化转动惯量与像素的灰度值、质心位置以及像素相对于质心的分布均有关。因此可以根据归一化转动惯量来区分不同的纹理。
由于本文只对微小像素块进行合并,因此仅仅对超像素分割结果图像中的微小像素块及其邻域像素块区域像素计算NMI值。
SLIC分割生成的超像素用集合S表示:

对于一幅M×N的数字图像,利用SLIC算法生成K个超像素块,根据多次实验,当N'<M×N/(20×K),则判定该超像素块为微小超像素块。N'为超像素块si中的像素个数。同时,统计微小超像素块的邻域超像素块,若只有一个邻域超像素块,则直接将该微小超像素块合并其中;若存在2个以上的邻域超像素块,则计算所有邻域超像素块的NMI值,并选择差异最小的邻域超像素块进行合并。
4 实验结果及分析
4.1 实验数据与引导滤波处理
本文使用2018年10月13日的浦东机场的高景一号01星图像进行算法验证。如图1所示,图1(a)为多光谱波段原始图像,分辨率为2 m,影像大小为1 423×892,影像中包括机场、飞机、跑道、建筑等。


图1 原图与各去噪算法的去噪图像Fig.1 Original image and denoising images of different denoising algorithms
一般遥感影像的噪声主要为高斯噪声[14],本文对原图添加了均值为0,方差为0.003的高斯噪声,噪声图像如图1(b)所示。此外,本文还利用基于广义高斯分布的小波软阈值去噪方法进行了实验对比,并计算滤波后图像与原图的PSNR值为评价指标,PNSR越高,与原图像越接近。实验结果如图1(c)~1(e)和表1所示。其中,图1(c)为采用高斯滤波器进行去噪的效果图,图1(d)为基于广义高斯分布的小波软阈值去噪效果图,图1(e)为采用引导滤波器进行去噪的效果图。经对比可以发现,在去噪、必要细节保留等综合性能上,引导滤波的处理效果明显优于其他两种滤波,引导滤波在去除噪声的同时,也较好地保存了边缘细节信息。结合表1也可以发现,引导滤波的PSNR值最高,滤波的效果最好。

表1 各种滤波方法处理后的PSNR值Tab.1 PSNR of different filtering algorithms
4.2 超像素初始分割
本文利用SLIC算法分别对图1中噪声图像和滤波图像进行初始分割,如图2所示,分割过程中选取的K=16,m=20。图2(a)为噪声图像图1(b)的初始分割结果,划分出5 959个超像素块。图2(a)中右图用不同颜色显示了图2(a)左图中不同超像素块,直观地展示了分割的类别划分结果。

图2 超像素初始分割结果Fig.2 Results of super pixel initial segmentation
为了直观展示分割结果,左图均为各超像素块的边缘轮廓图,右图均为各超像素块的颜色标签图。图2(b)为高斯去噪图像图1(c)的初始分割结果,划分出2 251个超像素块。图2(c)为去噪图像图1(d)的初始分割结果,划分出1 509个超像素块,图2(d)为去噪图像图1(e)的初始分割结果,划分出873个超像素块。显然,原始噪声图像由于含有最多的噪声,过分割现象最为严重。而相比于原始噪声图像,所有滤波后图像的超像素分割都得到了大幅度的改善。其中,经过小波软阈值滤波后图像相对高斯滤波结果有所改善,初始分割得到的超像素块相对较少,但是其效果依然不如引导滤波的效果。经过引导滤波的图像由于去噪效果最好,得到了更为理想的初始分割效果,各超像素块的边缘更贴近于真实的边缘。过于细碎的分割结果将直接影响后续的图像目标分类和其他分析。
4.3 合并超像素
针对图1中的所有含噪声的图像,利用本文算法进行微小超像素块的合并。实验结果如图3所示。同时,作为对比试验,本文也采用基于信息熵的方法进行微小超像素块的合并,合并前后的实验结果图和超像素块数量分别如图3和表2所示。和图2的展示类似,左图均为各超像素块的边缘轮廓图,右图均为各超像素块的颜色标签图。

表2 各图进行微小超像素合并前后的超像素数Tab.2 Comparison results of super pixel merging and non-superpixel merging

图3 超像素合并结果Fig.3 Results of super pixel merging
根据图3和表2可以发现,通过微小超像素合并后,各实验图像的过分割现象均得到了改善。以图3(g)和图3(h)为例,在经过上一环节的初始分割后,经过引导滤波后的图像被分割为873个超像素块,根据M×N/(20×K)计算出微小超像素块的阈值为72。对像素个数小于72的超像素块进行邻域合并,以信息熵为相似性度量准则进行合并后的分割结果图如图3(g)所示,合并后的超像素块数量为310;以NMI为相似性度量准则进行合并后的分割结果图如图3(h)所示,合并后的超像素块数量为282。对比图2(d)、图3(c)和图3(d),显然经过对微小超像素块的合并,图像的分割效果均得到了改善,本文所提方法的效果最好,并且得到的超像素块更加贴合边缘。同时,对比去噪前后的图像分割结果可以发现,未经去噪的图像图1(b)经过微小超像素块合并后,减少了约30%的微小超像素块。而对经过各种滤波处理的图像再进行微小超像素块合并,可以减少60%以上的微小超像素块。由此可见,图像去噪的预处理可以明显改善图像分割的效果。
综上所述,实验结果表明,本文所提的微小超像素合并算法可以更好的改善过分割现象。
5 结束语
本文提出的分割方法可以通过引导滤波器的预处理改善噪声点对超像素初始分割的影响,该方法在去除噪声的同时更好地保留了边缘信息。利用绕质心的归一化转动惯量进行超像素块之间的相似性度量,该特征不仅考虑了图像的空间信息,反映了图像颜色空间分布的复杂程度,更具有伸缩、平移和旋转不变性等优点,有效改进了在纹理复杂和相似区域的分割效果。实验结果表明,本文提出的分割方法可减小60%以上的微小超像素块,明显改善过分割现象,提升抗噪声干扰能力。
