双滚轮-导轨式渐开线测量仪的空间几何误差补偿方法
2022-03-31凌四营孔玉梅赵昌明王立鼎1
凌四营,孔玉梅,赵昌明,凌 明,王立鼎1,
(1.大连理工大学 精密特种加工教育部重点实验室,辽宁 大连116024;2.大连理工大学 微纳米技术及系统辽宁省重点实验室,辽宁 大连116024)
1 引 言
齿轮是量大面广的关键基础零部件,随着科学技术的不断发展,人们对齿轮精度的要求也越来越高。齿轮样板是一类用于齿轮量值传递基准与精度溯源的标准器件,包括齿轮渐开线样板、齿轮螺旋线样板和齿距样板等,其制造水平是一个国家齿轮技术实力的重要标志之一。其中,齿轮渐开线样板是校准各种渐开线测量仪器的标准计量器具,主要用于传递齿轮渐开线参数量值、修正仪器示值和确定仪器示值误差[1]。
我国有独立的齿轮渐开线样板国家标准GB/T 6467-2010[2],并定义了两个等级的齿轮渐开线样板,其中规定基圆半径rb≤100 mm的1级齿轮渐开线样板的齿廓形状公差不大于1μm。与同等基圆参数的1级精度标准圆柱齿轮相比,1级精度齿轮渐开线样板的展开长度扩大了约80%,而齿廓形状公差缩小了约40%。因此,1级精度齿轮渐开线样板的测量难度更高。目前商品渐开线测量仪器的测量不确定度都达不到1级渐开线的测量要求。因此,开展1级齿轮渐开线样板测量技术的研究具有重要意义。
齿廓偏差是齿轮精度评估的重要指标之一[2-3],在诸多测量渐开线齿廓偏差的测量仪器中,以齿轮测量中心(Gear Measuring Center,GMC)和三坐标测量机(Coordinate Measuring Machine,CMM)应用最为广泛[4]。对仪器的误差进行补偿是提升齿轮测量仪器的测量精度的常用技术手段。齿轮测量仪器的误差来源可分为系统误差和随机误差,其中系统误差主要包括空间几何误差、测头系统误差和测量方法误差等[5-7]。GMC和CMM的集成化程度高、功能强大、测量精度较高,但测量尺寸链长,精度提升空间有限,不满足1级齿轮渐开线样板的测量要求;国内外对两种仪器的精度提升研究已持续了几十年,主要从几何误差、数据处理软件优化、传感器精度、伺服路径规划和角度分度等方面提升精度[8-14]。
对比上述齿轮测量仪器,基于机械展成原理的双滚轮-导轨式渐开线测量仪结构更简单,尺寸链短,精度容易得到保证。滚轮-导轨式展成机构也是国内外普遍认可的具有最高展成精度的机构,该机构一般用于渐开线的精密测量领域[15]。对于该仪器,空间几何误差是其主要误差来源,包括驱动轴的位置误差、基圆盘及导轨的制造误差和各零件之间的安装误差等。一方面,关键零部件存在制造误差,且到某一公差后减小空间有限;另一方面操作人员会带来安装误差(如偏心、偏摆误差)。因此,探索出一种能够精确表征空间几何误差与齿廓偏差映射关系的测量方法,即利用零件的制造误差与安装误差互相抵消的补偿方法,对于渐开线测量精度的提升显得尤为重要。
针对双滚轮-导轨式渐开线测量仪,文献[16]分析了由基圆盘半径偏差引起的测量误差;文献[17]对基圆盘滚动精度展开了研究,并分析对比了不同的驱动方式对测量结果的影响;文献[18]分析了测量点偏差引起的测量误差;文献[19]分析了齿轮安装偏心对渐开线齿廓倾斜偏差的影响。以上文献都是针对仪器中的某一项误差源展开分析,对于其他误差源不具有普适性。文献[15]对仪器测量过程中的大多数误差源展开分析,补偿掉部分误差后仪器的测量不确定度可达0.31μm,但被测齿轮的展开长度较短,按照齿廓形状偏差的测量不确定度应不大于齿廓形状偏差最大允许公差的1/3的要求[20],该仪器仍然不满足1级精度齿轮渐开线样板的测量要求。
为了提升双滚轮-导轨式渐开线测量仪的精度,本文提出了一种空间几何误差补偿新方法,并基于该方法分析了基圆盘、齿轮渐开线样板与芯轴的综合安装误差和基圆盘的圆度误差对测量结果的影响,探索出装配误差和关键零部件的制造误差相互抵消的补偿方法,最后设计测量实验验证了空间几何误差补偿方法的有效性。
2 渐开线测量仪工作原理与齿廓偏差补偿模型
2.1 双滚轮-导轨式渐开线测量仪工作原理
双滚轮-导轨式渐开线测量仪的工作原理如图1所示,图中的滚轮由两个基圆盘组成,基圆盘与齿轮渐开线样板的基圆半径相同且同轴连接,当基圆盘在导轨上做纯滚动运动时,理论上渐开线与导轨平面的交点(即测量点)保持不动且该点在渐开线上的法线与基圆相切。实际的渐开线并不是一条理想的渐开线,故在实际测量过程中,测量点在水平方向上会产生偏移,该偏移量即表征被测渐开线的齿廓偏差。

图1 双滚轮-导轨式渐开线测量仪的工作原理Fig.1 Working principle of double roller-rail involute measuring instrument
双滚轮-导轨式渐开线测量仪的测量过程如下:将纯滚动组件(如图2所示,由两个基圆盘、齿轮渐开线样板和芯轴等组成)放置到导轨上,并紧贴于基圆盘定位挡板以校正滚动方向;调整测头测量方向与导轨平行并使测量点位于导轨平面内;驱动装置带动纯滚动组件沿着水平方向滚动的同时,数据采集系统开始实时采集被测渐开线的齿形信息,最后根据采集的数据计算出被测渐开线的齿廓偏差。

图2 纯滚动组件Fig.2 Pure rolling component
该测量方法的精度很大程度上依赖于展成机构的展成精度,其中基圆盘是展成机构中的最关键零件,它的制造误差和装配误差是影响测量精度的主要误差源。此外,测点的位置误差、导轨的平面度误差、两条导轨之间的平行度误差、齿轮渐开线样板与芯轴的装配误差等也会影响测量结果。
2.2 齿廓偏差补偿模型的建立
齿廓偏差补偿模型旨在建立原始误差、机构和运动参数与齿廓偏差之间的数学关系,是空间几何误差分析的理论基础和关键,通过模型建立的数学关系,修正仪器的示值误差,提高渐开线齿廓偏差的测量精度。
为此,先建立两个空间坐标系:仪器坐标系OwXwYwZw和工件坐标系ObXbYbZb。OwXwYwZw坐标系中的坐标原点Ow为理想状态下测量点初始所在位置,Xw轴指向导轨的延伸方向,Yw轴指向平行于芯轴轴线方向,Zw轴指向竖直方向。ObXbYbZb坐标系中的坐标原点Ob为被测样板的中心,Xb轴指向被测样板中渐开线起始点与样板中心的连线方向,Yb轴指向芯轴轴线方向,Zb轴指向同时垂直于Xb轴和Yb轴的方向,如图3所示。

图3 仪器坐标系与工件坐标系示意图Fig.3 Diagram of the machine coordinate system and the workpiece coordinate system
仪器坐标系的位置是固定的,而工件坐标系的位置随着基圆盘的滚动不断发生变化,工件坐标系相对于仪器坐标系有6个自由度,故存在6个空间几何误差,如图4所示,分别为3个线性误差ex、ey、ez和3个旋转误差r x(ObXbYbZb坐标系绕Xw轴的旋转角)、r y(ObXbYbZb坐标系绕Yw轴的旋转角)、rz(ObXbYbZb坐标系绕Zw轴的旋转角)。其测量原理是计算出实际测量过程中测球与渐开线接触点与理论接触点在仪器坐标系OwXwYwZw中的Xw轴坐标之差Δ。

图4 空间几何误差引起测量误差的原理Fig.4 Principle of measurement error caused by spatial geometric errors
2个线性误差ex、ez和3个旋转误差r x、ry、r z都会导致测量点产生偏移。ey单独出现时对测量不产生影响,当ey与r x或r z同时出现时便会对测量结果产生影响。若被测样板存在线性误差ey和旋转误差r x,如图4(a)所示,测球与渐开线齿廓的接触点将向上偏离于理论所在渐开线齿廓面的位置,此时可等效为齿轮渐开线存在线性误差ezr,这两者之间的转换关系为:

其中,r为齿轮渐开线样板的基圆半径。
若被测样板存在线性误差ey和旋转误差rz,如图4(b)所示,测量点将产生Xw轴方向的偏移,偏移量exr为:

其中,S为基圆盘滚动距离,其值等于基圆半径r与滚动角度φ的乘积,即S=rφ。
若被测样板存在旋转误差ry和线性误差ex、ez,如图4(c)所示,通过几何方法计算测量点的偏移量过程复杂,且一般求得的是近似解,精度稍显不足。因此这里采用坐标系变换的方法:先求得实际测量点P'在工件坐标系ObXbYbZb中的坐标(xb,yb,zb),再通过坐标系变换求得该点在仪器坐标系OwXwYwZw中的坐标(xw,yw,zw),最后与理论测量点P在仪器坐标系中的坐标进行对比,从而得到测量误差。由式(1)、(2)计算得到的ezr和exr都可以算入此种情况中的ez和ex。
图4(c)中,r为理论基圆半径,f1(ζ)为渐开线齿廓,f2(t)为测头装置中测杆所在直线,P'为实际测量点,P为理论测量点,ζ为实际测量点处的渐开线展开角,φ为理论测量点处的渐开线展开角。在XbObZb平面中,渐开线f1(ζ)的参数方程为:
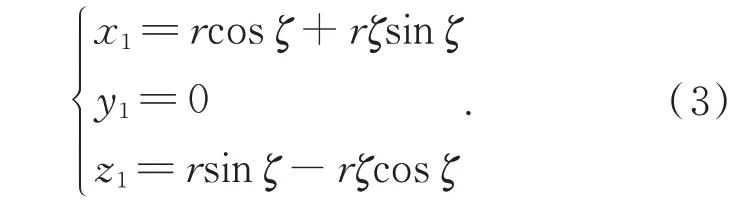
直线f2(t)在XbObZb平面中的参数方程为:
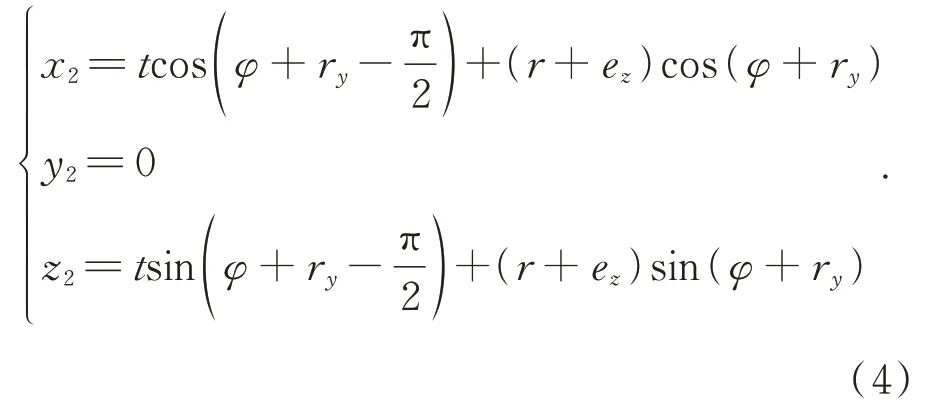
渐开线f1(ζ)与直线f2(t)在XbObZb平面内的交点联合式(3)(4)可求得:
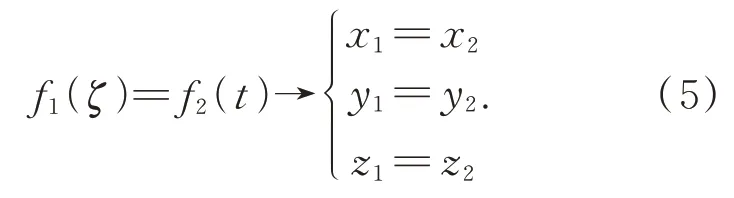
式(5)的解析解计算过程繁杂,但是数值解利用MATLAB软件编程求解相对简单得多,计算得到参数t、ζ,选其中一个代入相应的参数方程中,即可求得点P'在工件坐标系ObXbYbZb中的坐标(xb,yb,zb)。然后根据两个坐标系的位姿关系,将ObXbYbZb坐标系绕Yw轴旋转η=(φ+ryπ/2)角度,再沿Xw轴平移(ex+rφ)个单位,最后沿Zw轴平移(r+ez)个单位,求出实际测量点P'在仪器坐标系OwXwYwZw中的坐标(xw,yw,zw):
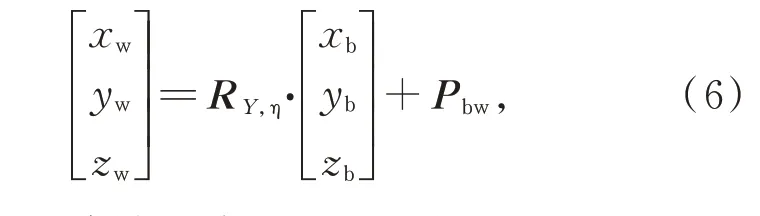
其中:R Y,η为旋转矩阵,Pbw为平移向量,可由下式计算:

由于理论测量点P位于仪器坐标系的原点,故式(6)中实际测量点P'的横坐标xw即为测量误差Δ。

在展开长度ρs范围内取多个测量点,所有点带入式(8)获得一条测量误差曲线,从测量误差曲线中能分离出齿廓总偏差Fα、齿廓倾斜偏差fHα和齿廓形状偏差ffα。如图5所示为测量误差曲线的齿廓偏差示意图。
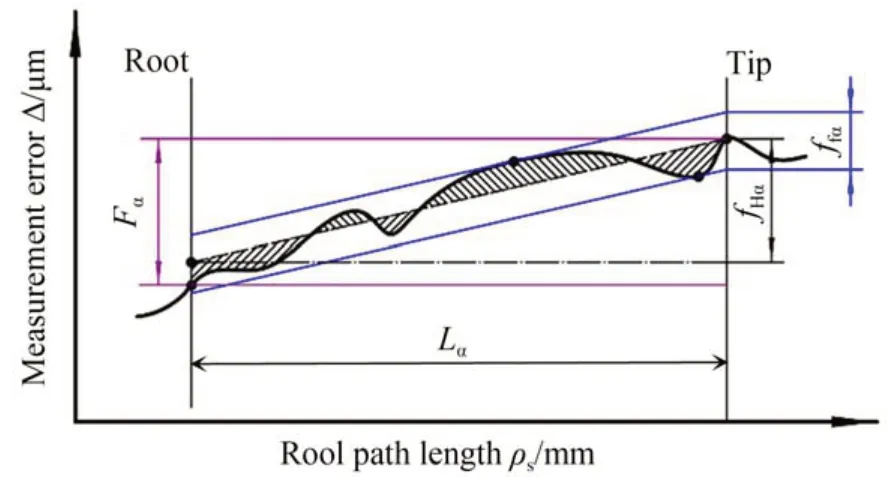
图5 测量误差曲线的齿廓偏差示意图Fig.5 Diagram of the profile deviation of the measuring error curve
3 主要的空间几何误差源分析
上节分析的齿廓偏差补偿模型能将6个空间几何误差对测量结果的影响计算出来。只要知道6个空间几何误差量,带入模型便能计算出其带来的齿廓偏差。本节针对双滚轮-导轨式渐开线测量仪的主要两项空间几何误差源展开具体分析。
3.1 基圆盘的圆度误差
采用展成法测量渐开线的精确度在一定程度上依赖于基圆盘的各项精度指标。基圆盘的圆度误差以椭圆形状居多,本文针对此种情况带来的测量误差进行分析。基圆盘的圆度误差会导致实际展开长度与理论展开长度不相等,从而产生线性误差ex1;此外,两个基圆盘的滚动距离也可能不等,进而导致芯轴产生旋转误差r z1;由于圆度误差,基圆盘圆心到外圆的距离(即基圆盘的极径)不等于理论基圆半径r,从而导致被测样板中心与理论位置存在线性误差ez1及旋转误差r x1。图6为基圆盘的圆度误差带来的空间几何误差示意图。
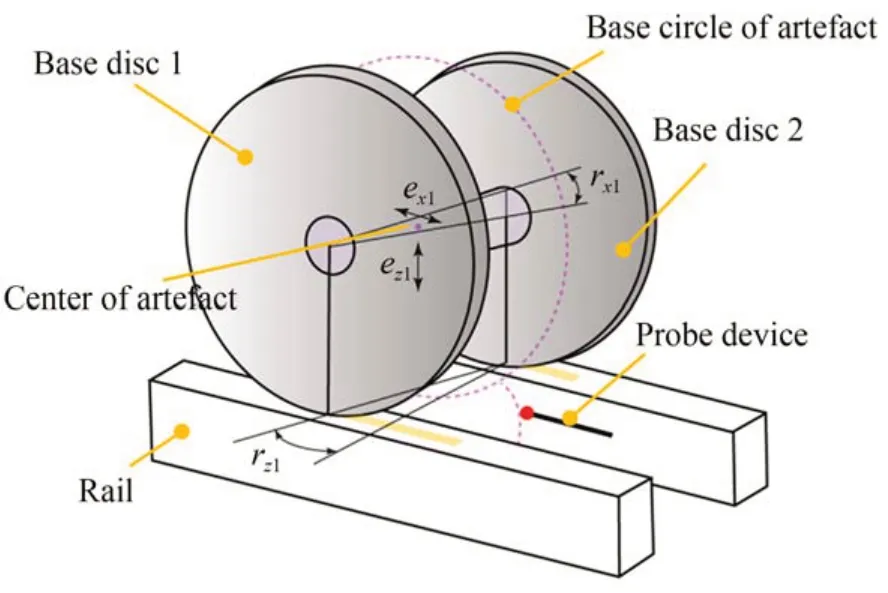
图6 基圆盘的圆度误差带来的空间几何误差Fig.6 Spatial geometric errors caused by the roundness error of the base discs
设基圆盘1的长短轴半径分别为a1、b1,基圆盘2的长短轴半径分别为a2、b2,则圆度误差κ=a-b。当基圆盘转过φ角,被测样板中心偏离于其理论所在位置的距离为:

其中:ρ1、ρ2分别为φ角时基圆盘1、基圆盘2的极径。ρ1、ρ2可由下式计算:
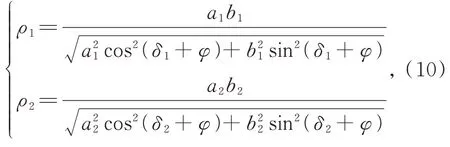
其中:δ1、δ2分别为基圆盘1、基圆盘2的初始极角,即基圆盘与导轨接触点处的极径和椭圆长轴之间的夹角。
齿轮渐开线样板相对于仪器坐标系的旋转误差r x1为:
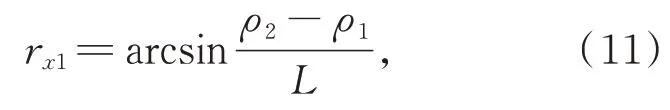
其中,L为芯轴的长度。
线性误差ex1可由下式计算:

齿轮渐开线样板相对于仪器坐标系的旋转误差rz1为:

基圆半径r为100 mm的齿轮渐开线样板,展开角θ在0°~40°,展开长度ρs在0~70 mm。将基圆盘的圆度误差引起的空间几何误差ex1、ez1、rx1、r z1带入2.2节所述齿廓偏差补偿模型,根据式(8)计算出测量误差Δ1并分析得出以下结论:(1)当基圆盘的圆度误差κ一定时,其引起的齿廓偏差随着两个基圆盘的初始极角δ1、δ2的变化而变化,且主要带来的是齿廓倾斜偏差fHα;(2)当滚动区域对称分布在两个椭圆长轴(初始极角δ1=δ2=-θ/2=-20°)或 短 轴(δ1=δ2=(π-θ)/2=70°)时,带来的齿廓总偏差Fα最大且相等,其中齿廓倾斜偏差fHα互为相反数。
图7为基圆盘的圆度误差引起的齿廓偏差与初始极角的关系曲线,δ1与δ2的取值范围为[-90°,90°],展开长度ρs在0~70 mm,为方便与实验结果对比分析,两个基圆盘的圆度误差分别取值为0.4 mm和0.6 mm。

图7 齿廓偏差与初始极角关系Fig.7 Relationship between the profile deviation and initial pole angle
3.2 纯滚动组件的综合安装误差
基圆盘的制造误差除了外圆柱面的圆度误差,还包括内孔的制造偏心等,此外,操作人员的技术水平也会带来基圆盘和样板的安装偏心、偏摆问题。纯滚动组件的综合安装误差包括基圆盘和样板相对于芯轴的综合安装偏心误差和综合安装偏摆误差。基圆盘若存在安装偏摆,则滚动圆周为椭圆形状,故基圆盘的安装偏摆误差对齿廓偏差的影响可等效于基圆盘的圆度误差带来的影响;齿轮渐开线样板的安装偏摆误差等效于芯轴在两个基圆盘内孔中安装偏心方向相反的情况。因此这里对基圆盘和齿轮渐开线样板的安装偏摆误差不做详细分析,仅讨论综合安装偏心的情况。
图8为纯滚动组件的综合安装偏心示意图。图中O1、O2、O3分别为基圆盘1、基圆盘2和样板的圆心;e1、e2分别为芯轴在基圆盘1、基圆盘2的偏心量,e3为样板在芯轴上的偏心量;λ1、λ2分别为芯轴相对于两个基圆盘的偏心相位角(芯轴和基圆盘内孔圆心的连线与水平轴之间的夹角),λ3为样板相对于芯轴的偏心相位角。λ1、λ2不相等会导致被测样板产生偏摆,即存在旋转误差rx2和r z2。

图8 纯滚动组件的综合安装偏心示意图Fig.8 Comprehensive installation eccentricity diagram of a pure rolling component
综合安装偏心导致样板相对于仪器坐标系产生4个空间几何误差:ex2、ez2、r x2和r z2,当基圆盘转过角度φ时,水平方向产生的线性误差ex2为:

旋转误差rx2可由下式计算:

将上式带入式(1)进而求得ez2:

旋转误差rz2可通过下式求得:
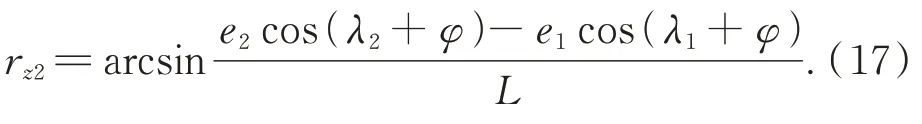
将ex2、ez2和r z2代入式(8)即可求得测量误差Δ2。利用MATLAB对式(3)~(8)、(14)~(17)进行编程,画出当三个偏心量e相等时,在展开长度ρs为0~70 mm范围内齿廓偏差与三个偏心相位角的关系曲线,如图9所示。为方便与实验结果进行对比,偏心量的值取为3.46μm,分析得出以下三点结论(适用于三个偏心量相等的所有情况):

图9 齿廓偏差与偏心相位角关系Fig.9 Relationship between the profile deviation and the eccemtric phase angle
(1)当偏心相位角λ1=λ2且与偏心相位角λ3相差180°时,综合安装偏心对测量结果没有影响;
(2)当偏心相位角λ1=λ2=λ3=70°或250°时,综合安装偏心带来的齿廓倾斜偏差fHα最大;
3)当偏心相位角λ1=λ2=λ3=160°或340°时,综合安装偏心带来的齿廓形状偏差ffα最大,不带来齿廓倾斜偏差。
图10为极限齿廓偏差f[max]与偏心量e的关系。由图可知,极限齿廓偏差与偏心量成正比关系,其 中 极 限 齿 廓 倾 斜 偏 差fHα[max]为 偏 心 量 的136%;极 限 齿 廓 形 状 偏 差ffα[max]为 偏 心 量 的12%。

图10 极限齿廓偏差f[max]与偏心量e的关系曲线Fig.10 Relationship curve between the extreme profile deviation f[max]and the eccentricity e
4 实验验证
为了验证齿廓偏差补偿模型的有效性,针对上节分析的两项空间几何误差源设计相应实验。实验在室温为20±0.5℃的大连理工大学高精度测量间进行,所有数据均重复5次测量,取平均值作为最终测量结果。
4.1 实验准备
实验前需要测量两个基圆盘的圆度误差大小和滚动组件装配过程中的实际综合安装偏心大小。基圆盘的圆度误差测量如图11所示,选用分辨力为0.1μm的便携式电感测微仪,电感测头打在两个基圆盘外圆和样板两侧端面上(样板的径跳取两侧端面径跳值的平均值),转动芯轴至下一个测量点,直至芯轴转动一周。由于此测量方法以顶尖为基准,因此需要将芯轴顶尖孔相对于各安装轴段的偏心考虑进去,根据径向跳动测量值拟合计算出基圆盘的圆度误差,如图12所示,基圆盘1的圆度误差κ1=0.4μm,基圆盘2圆度误差κ2=0.6μm。

图11 两个基圆盘的圆度误差测量Fig.11 Roundness error measurement of the two base discs

图12 两个基圆盘的圆度误差Fig.12 Roundness error of the two base discs
纯滚动组件的综合偏心通过加装G5级球制作的、具有微量过盈量的偏心密珠轴套实现[21],图13为特制偏心密珠轴套示意图,移除密珠轴套均布六球室中Y方向的对称两球室里的球,在锁紧螺母和平垫圈的作用下,被测工件偏心方向基本与Y方向一致,可通过更换不同直径的密珠满足不同偏心量的需求。

图13 偏心密珠轴套Fig.13 Eccentric multi-ball bearing
用偏心密珠轴套依次装配出如图14中三种位姿的纯滚动组件。装配时控制不同位姿下的渐开线展开长度对应的基圆盘区域相同,芯轴与基圆盘的对应相位也相同,确保测量过程中只有综合安装偏心这一个变量影响测量结果。

图14 三种综合偏心装配位姿Fig.14 Three comprehensive installation eccentric positions
综合偏心的测量方法和基圆盘的圆度误差测量方法相似,补偿掉芯轴顶尖孔相对于各安装轴段的偏心后,计算出滚动组件的真实综合安装偏心值。偏心相位角λ1=λ2=λ3=70°情况下滚动组件的综合安装偏心值如图15所示,从图中可以看出偏心量为3.46μm,偏心相位的误差为±2°。

图15 λ1=λ2=λ3=70°时纯滚动组件的综合安装偏心Fig.15 Comprehensive installation eccentricity of the pure rolling element whenλ1=λ2=λ3=70°
4.2 实验过程与结果
实验所用齿轮渐开线样板的基圆半径r为100 mm,展开长度ρs在0~70 mm,评测计值区间Lα为5~70 mm。
为了验证基圆盘的圆度误差对测量结果的影响规律,将齿轮渐开线样板的展开长度ρs对应的基圆盘圆弧段(即滚动区域)选取为三个不同区段,分别为对称分布在椭圆长轴(初始极角δ1=δ2=-20°)、对称分布在椭圆短轴(δ1=δ2=70°)和分布在长短轴之间(δ1=δ2=25°)。根据3.1小节的分析,δ1=δ2=-20°和δ1=δ2=70°带来的齿廓倾斜偏差互为相反数,δ1=δ2=25°带来的齿廓倾斜偏差为零,具有明显的对比特征。
按上述初始极角值依次装配好后将纯滚动组件放置到实验室自行研制的齿轮渐开线样板激光干涉测量装置上,测量齿轮渐开线样板的齿廓偏差,如图16所示。该测量装置整合了双滚轮-导轨式展成机构和任意表面形位误差的激光测量测头装置,导轨的直线度误差为20 nm/120 mm,激光干涉仪的测量精度约为15 nm,测量装置补偿部分误差后对于渐开线齿廓偏差的测量不确定度可达0.4μm,精度符合实验需求。

图16 基圆盘的圆度误差引起的齿廓偏差测量实景Fig.16 Real scene of tooth profile deviation measurement caused by roundness error of base disc
基圆盘的圆度误差引起的测量误差的实测曲线Δ1'如图17所示,图18为根据齿廓偏差补偿模型画出的滚动区域不同时的理论偏差曲线Δ1。
从图17可以看出,在计值范围Lα内,初始极角δ1=δ2=25°时的实测曲线相对于δ1=δ2=-20°时的实测曲线,齿廓倾斜偏差fHα减小了0.11 μm,齿廓形状偏差ffα增大了0.04μm;δ1=δ2=70°时的实测曲线相对于δ1=δ2=-20°时的实测曲线,齿廓倾斜偏差fHα减小了0.31μm,齿廓形状偏差ffα基本不变;与图18中三条理论曲线的齿廓偏差变化规律基本一致。

图17 滚动区域不同时的实际测量曲线Fig.17 Actual measurement curve for different rolling areas

图18 滚动区域不同时的理论偏差曲线Fig.18 Theoretical deviation curve for different rolling areas
表1为滚动区域不同时的测量结果,表中齿廓偏差理论值可通过图7查找。从表1可以看出,将δ1=δ2=25°和δ1=δ2=70°的测量曲线减去δ1=δ2=-20°的测量曲线后(即#i-#1),在计值范围Lα内实际齿廓偏差与理论齿廓偏差的差值不大于0.04μm。

表1 滚动区域不同时的测量结果Tab.1 Measurement results of different rolling area
为了验证齿廓偏差补偿模型的正确性,还针对基于齿廓偏差补偿模型分析的综合安装误差设计实验验证。依次测量偏心量为3.46μm的三种综合偏心装配位姿下被测样板的齿廓偏差,所测得的实际误差曲线Δ2'如图19所示,理论偏差曲线Δ2如图20所示。
从图19可以看出,偏心相位角λ1=λ2=λ3=160°的实测曲线相对于λ1=λ2=-20°、λ3=160°的实测曲线,齿廓形状偏差ffα增大了0.43μm,约为偏心量的12%,齿廓倾斜偏差fHα不变;λ1=λ2=λ3=70°的实测曲线相对于λ1=λ2=-20°、λ3=160°的实测曲线,齿廓倾斜偏差fHα减小了4.62μm,约为偏心量的134%,齿廓形状偏差ffα基本不变;与图20中三条曲线的齿廓偏差变化规律基本吻合。

图19 不同综合安装偏心下的实际测量曲线Fig.19 Actual measurement curve of different comprehensive installation eccentricity
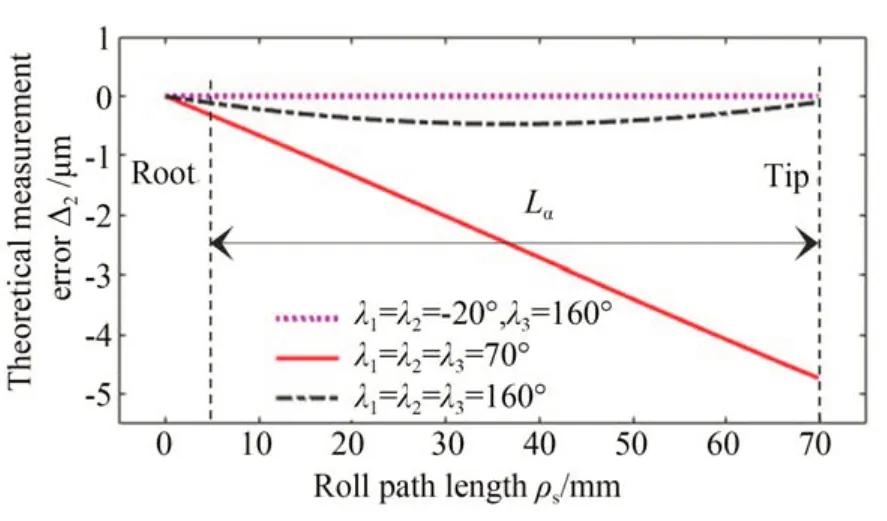
图20 不同综合安装偏心下的理论偏差曲线Fig.20 Theoretical deviation curve of different comprehensive installation eccentricity
表2为不同装配位姿下的测量结果,表中齿廓偏差理论值可通过图9查找。从表2中可知,(#2-#1)的实际齿廓倾斜偏差与理论值的差值为-0.16μm,相对误差约为4%;(#3-#1)的实际齿廓形状偏差与理论值的差值为0.01μm,相对误差约为2%。

表2 不同综合安装偏心下的测量结果T ab.2 Measurement results in different comprehensive installation eccentricity
考虑到测量装置的系统误差、测量重复性误差和偏心相位误差,测量结果与理论结果存在偏差在所难免。
实验结果表明齿廓偏差补偿模型能够有效表征空间几何误差与渐开线齿廓偏差之间的计算关系,可通过安装误差之间的相互抵消或直接补偿提高双滚轮-导轨式渐开线测量仪的测量精度。
除此之外,在实验过程中我们发现将两个基圆盘和被测样板调整成无偏心十分困难。相比之下,相位则容易得到控制,因此可以采用图14(c)方式补偿修正滚动组件综合安装偏心带来测量误差。
5 结 论
本文针对双滚轮-导轨式渐开线测量仪器中存在的空间几何误差提出了一种补偿新方法,该方法避免了超越方程求解一般公式的复杂性,只需确定几何误差量便能通过齿廓偏差补偿模型直接计算出其带来的齿廓倾斜偏差和齿廓形状偏差;然后基于该补偿模型对几项常见的空间几何误差源(如渐开线样板、基圆盘与芯轴的综合安装误差,基圆盘的圆度误差等)进行具体分析,得出初始误差与齿廓偏差之间的映射关系,并对其进行实验验证,得到如下结论:
(1)将渐开线的展开长度区域选在基圆盘的不同使用圆弧段,实验证明当滚动区域对称分布在椭圆的长轴或短轴时,带来的齿廓倾斜偏差最大,且方向相反,实测值与理论值的绝对误差不大于0.04μm。
(2)齿轮渐开线样板、基圆盘与芯轴的安装偏心对齿廓偏差影响很大,其值的大小与偏心相位角相关。当偏心相位角λ1=λ2=λ3=70°时,带来的齿廓倾斜偏差最大,与理论值的相对误差约为4%;当偏心相位角λ1=λ2=λ3=160°时,带来的齿廓形状偏差最大,与理论值的相对误差约为2%。
实验结果证明了空间几何误差补偿方法的有效性,该补偿方法为实现基准级齿轮渐开线样板的制造提供了测量手段。
