基于差极结构的绝对式直线时栅位移传感器研究及测量误差特性分析

2022-03-31陈自然冯曦颉陈鸿友张桁潇余海游

光学精密工程 2022年6期

陈自然，黎锡，冯曦颉，陈鸿友，张桁潇，余海游

（1.重庆理工大学机械检测技术与装备教育部工程研究中心，重庆400054；2.时栅传感及先进检测技术重庆市重点实验室，重庆400054）

1 引言

精密位移测量技术及器件是高端数控机床、科学仪器装置和国防军工系统等高精尖装备的核心技术和关键功能部件，其水平直接决定着系统的整体性能。工业的不断发展，迫切需求能够实现高精度、高分辨力的绝对式位移传感器。相比增量式位移传感器，绝对式位移传感器可有效消除累计误差，提高测量精度和加工效率，是现今位移传感器研究的热点［1-3］。

绝对式光栅位移传感器是目前研究最多、应用最广的绝对式位移传感器，其测量原理是将不同宽度和不同间距的栅线以绝对位置数据编码的形式直接制作到标尺上用来确定绝对位置。目前主流的三种编码技术分别为单码道伪随机码编码方式、多轨二元伪随机码编码方式和多轨P元伪随机码编码方式。单码道伪随机码编码方式由增量编码与绝对编码相结合，围绕M-序列方式生成全程位置单值函数的伪随机码，绝对码道代表周期位置，增量码道代表周期内细分位置，组合后方得高分辨力的绝对位置值［4-8］。多轨二元伪随机码编码方式在单码道基础上又多加了几道伪随机码道，上一条码道比下一条码道少一个周期［9-11］。多轨P元伪随机码编码方式是在原有的单码道伪随机编码上多增加了几位编码，有效地降低了误码率［12-14］。为降低读取编码的误码率，海德汉公司创新性地设计了一套冗余结构的光学系统，将照明系统发出的平行光源等分成两路，同时反射到光栅主尺的两条不同码道上，大大提高光栅尺读数系统的稳定性和可靠性［15］。无论哪种编码都需要考虑在有限的空间范围内布置大量无重复位置编码，并要考虑编码可扩展、易处理、容错、冗余等多方面因素，因而技术难度高［16-17］。另外，易受光源和编码表面污染引起的散射影响等问题，使得图像采集耗费时间长，解码算法较复杂［18-19］。西方发达国家将光栅绝对编码列为国家顶级战略技术和商业机密加以封锁。以上问题都严重制约着我国绝对式光栅的进一步发展。

针对上述问题，本文在前期原创成果增量式时栅位移传感器的基础上，提出一种“精机定位+精机测量”多尺度组合测量技术实现高精度绝对位移测量，可有效回避精密绝对式位移传感器对编码技术和超精密加工的过度依赖，实现精密绝对位移测量。

2 绝对位移传感器结构及测量原理

2.1 绝对位移传感器结构

绝对式时栅位移传感器的结构主要由动尺和定尺组成，如图1（a）所示。其中动尺包含两列感应绕组和导磁基体，定尺包含两列激励绕组和导磁基体。动尺的感应绕组由n个正弦形线圈首尾相接串联而成，如图1（b）所示。定尺的激励绕组由正弦绕组s和余弦绕组c按照“几”字形空间相差四分之一极距均匀排列，如图1（c）所示。单列激励绕组和感应绕组分解图如图1（d）所示。在量程L范围内，将具有N对极数的激励绕组命名为激励绕组1，其极距为W1，将具有N-1对极数的激励绕组命名为激励绕组2，其极距为W2。为增加信号强度，减少线圈匝数，将定尺和动尺均固定在导磁基体上。

图1 传感器结构示意图Fig.1 Diagram of sensor structure

2.2 位移传感原理

以激励绕组1和感应绕组1为例，对单列位移传感原理进行分析。当定尺激励绕组1中的正弦绕组s和余弦绕组c分别通入正弦交变电流is=Imsin（ωt）和余弦交变电流ic=Imcos（ωt）时，产生的磁场磁感应强度分别为Bs和Bc，其表达式为：

其中：k为比例系数，Im为交变电流的幅值，ω为交变电流的频率。

在Bs和Bc的共同作用下，激励绕组1周围形成随时间均匀变化的时变磁场。根据法拉第电磁感应定律，动尺感应绕组1的半正弦形线圈沿X轴方向移动过程中拾取时变磁场，设半正弦线圈的数学模型为：

图1（d）下半部分为余弦绕组c在交变电流ic作用下，半正弦形线圈拾取磁场的示意图。设半正弦线圈的高为h，宽为W1/2，O为半正弦线圈的运动始点，x为其位移量。余弦绕组c产生的磁感应强度在矩形范围内沿X轴方向呈正反交替变化。因此在极距W1范围内，根据变上下限积分，可求得半正弦线圈在［0，W1/2］和［W1/2，W1］两个区间的磁通量Φ1(t，x)，如式（3）所示：

同理，当半正弦线圈在通入正弦交流电流is时，其在极距W1内产生的磁通量Φ2(t，x)为：

由于式（3）、式（4）是感应绕组1半正弦形线圈在激励绕组1的余弦绕组c和正弦绕组s沿X轴方向运动一个极距的磁通量。所以n个半正弦形线圈串联的感应绕组1沿X轴在整量程内运动N个极距，磁通量包络线以极距为单元周期性变化N次，其感应电动势为：

感应绕组1则可得到感应电动势ε1、ε2的叠加信号U1：

同理，感应绕组2在运动N-1个极距范围内，感应信号为：

2.3 绝对位移信号解耦模型

感应信号U1、U2都包含了绝对位移信息x，由于两列周期性传感结构对极数相差为1，在整个测量范围内，两列感应信号相差一个周期，因而可以采用“精机定位+精机测量”进行绝对位移信息解耦。

将感应绕组的输出信号通入信号处理电路进行信号处理，得到整形后的方波信号，并将其传入FPGA芯片中，与其内部产生的同频、相位固定的参考信号Uf进行比相，采用高频时钟插补技术进行计数得到U1、U2信号对极内的相位差φ1、φ2。而将两路感应信号互相比相得到的相位差为Δφ。当传感器动尺相对于定尺沿X轴方向距离为x时，则动尺相对于定尺移动的位移x与移动的对极数n1、n2及对极内相位差φ1、φ2之间的关系为：其中，对极数n1、n2可由下式求得：

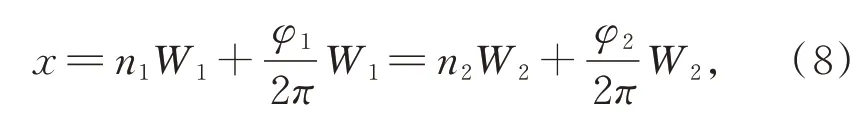
传感器的测量分辨力可以表示为：

其中：L是量程，N是对极数，fe是激励信号频率，fr是用于插补相位差的时钟频率。

传感器的线性度可表示为：

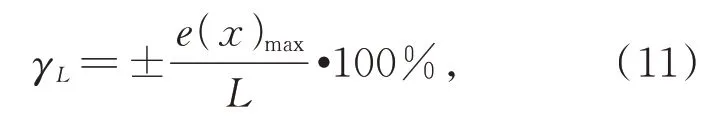
其中：e(x)max是非线性最大偏差，L是满量程输出。

图2为绝对位移测量原理图，包含激励信号的产生、感应信号处理和位移信号解算三大部分。其中激励信号is、ic是由FPGA产生的，如图2（a）所示。通过D/A转换和功率放大后将产生的激励信号is、ic分别通入正弦、余弦激励绕组，如图2（b）所示。采用动尺上的感应绕组感应磁场，得到两路行波信号U1、U2，如图2（c）所示。经过放大、滤波、过零比较等电路处理后得到两路整形后的方波信号，分别与参考信号Uf比相得相位差为φ1、φ2，并将两方波信号比相得到相位差Δφ，通过高频时钟脉冲插补计数转换得到位移量，如图2（e）所示。图2（f）、（g）分别为传感器精机定位与精机测量的示意图。图2（g）中，n1是精机定位中动尺移动的对极数，由式（9）可计算得到。精机测量是对极内的位移值进行精确测量，如图2（g）中的x1表示的位移。最后将精机定位测量结果与精机对极内测量结果如式（8）相加，可得到最后绝对式位移测量值。

图2 绝对位移测量原理图Fig.2 Schematic diagram of absolute displacement measurements

3 测量误差和精度分析

3.1 安装高度对测量精度影响分析

激励电流产生的感应磁场强度在不同气隙高度的磁场分布不同，为了分析传感器不同气隙高度对测量精度的影响，通过Solidworks建立三维仿真模型，设置不同的气隙高度，在Ansoft Maxwell中进行有限元电磁场仿真［20］。在一个对极18 mm范围内，5种不同气隙高度所感应的位移信号的测量误差如图3所示。

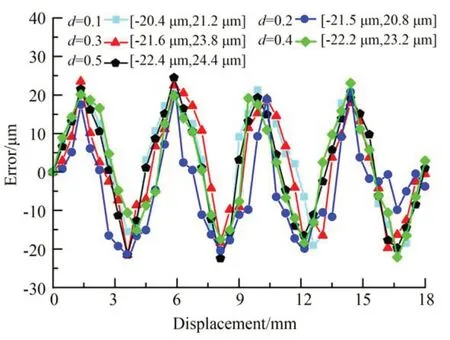
图3 传感器不同气隙对极内的测量误差曲线Fig.3 Measurement error curves in different air gaps of the sensor

对感应绕组1在一个对极内不同气隙高度的位移测量误差进行傅立叶变换分析，得到如图4所示的测量误差谐波频谱图。分析结果表明在对极内不同气隙高度对应的位移测量误差主要包含直流分量、一次谐波和四次谐波。当气隙高度d大于0.2 mm时，随着气隙d逐渐增大，直流分量和一次谐波呈增大趋势，四次谐波则呈现不断减小趋势。而当气隙高度d小于0.2 mm时，由于受正、余弦交变电流较大的影响，二次、三次和五次谐波误差有明显增加。究其原因在于气隙高度越低，磁感应强度越强，各谐波成分幅值也明显较大。随着气隙高度不断增加，高次谐波幅值衰减明显。综合考虑感应信号幅值、测量误差及谐波成分等因素，采用气隙高度d为0.2 mm。

图4 不同气隙高度对应对极内测量误差频谱图Fig.4 Spectrogram of measurement error for different heights of air gap

3.2 安装偏转角对测量精度影响分析

针对传感器安装偏转角导致的空间相位非正交误差进行讨论，如图5所示。安装时左边的感应半正弦线圈中心点相对于原有的位置沿X轴负方向产生了-Δx偏差，而右边的半正弦则相反，这种安装偏差会导致两正弦形线圈感应的两路驻波的空间相位非正交。

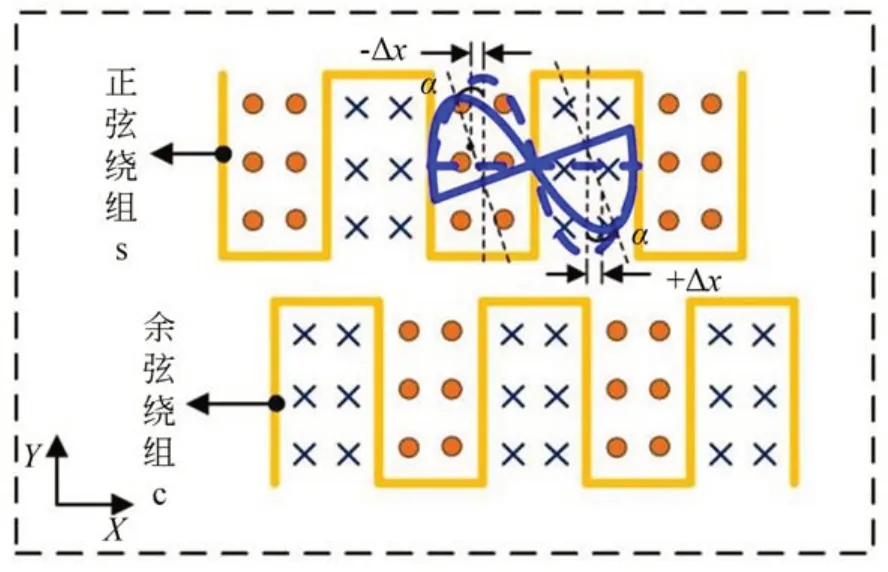
图5 传感器安装偏转Fig.5 Sensor installation with a deflection angle

以激励绕组1为例，由于相位偏差是对应关系，设正弦路为基准，余弦路驻波信号在空间上相对于正弦路偏差的角度为α，此时传感器感应信号U1为：

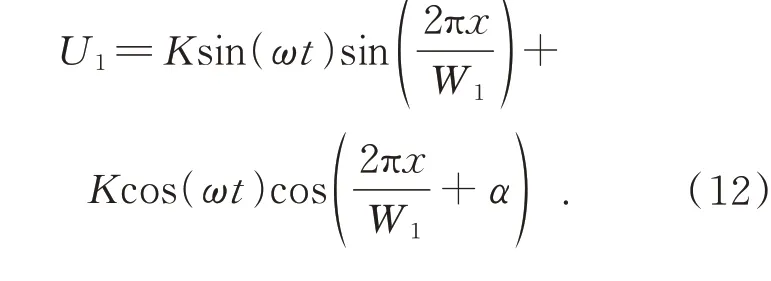
由于三角函数公式为：

则由式（12）、（13）可得：

由式（14）可得测量误差e(x)为：

因此，当传感器安装偏转角度误差导致的两路驻波信号在空间上非正交时，其引入的测量误差e（x）在对极内表现为直流误差和二次谐波误差。

采用空气气隙高度d为0.2 mm进行仿真，反偏转方式如图5所示，将感应绕组1的线圈按正、反方向分别偏转0.5°、1°进行仿真，仿真结果显示当偏转角度增大，对极内测量误差呈现明显增加趋势，如图6所示。采用傅立叶变换对测量误差进行分析，得到如图7所示的测量误差频谱图。分析结果表明对极内的测量误差主要集中为直流分量、二次谐波和四次谐波，其中直流分量和二次谐波误差在前六次谐波分量中占比分别为24.7%和39.2%。结合上述理论分析可知感应绕组1的线圈偏转会引入直流误差和二次谐波误差分量，与仿真结果相吻合，仿真证明了理论分析的正确性。

图6 不同偏转角的对极内测量误差Fig.6 Measurement errors within a pole for different deflection angles

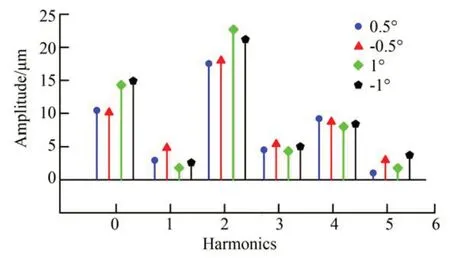
图7 不同偏转角对极内的测量误差频谱图Fig.7 Spectrogram of measurement error within a pole for different deflection angles

4 实验研究

为了检测基于差极结构的绝对式直线位移传感器的测量精度，搭建了如图8所示的实验平台，其中：①为激光干涉仪上位机，②为直线电机控制系统，③为传感器精度检测上位机，④为电源模块，⑤为信号处理电路板，⑥为Tektronix示波器，⑦为传感器样机，⑧为直线电机，⑨为Renishaw激光干涉仪XL-80。直线电机采用美国AEROTECH公司的制造的直线电机模组PRO190LM-0500-TT 1-E3-CMS1-LFPL 2-TAS，配置高性能驱动器BLMC-192-A，系统重复精度为±0.5μm，系统整体定位精度±1μm，分辨力为10 nm。传感器采用PCB工艺加工而成。实验中将传感器动尺和定尺分别固定于导磁钢基体上，通过直线电机运动平台带动传感器的感应绕组沿导轨做直线移动。感应的两路行波信号经过信号处理转换成两路方波，其相位之差作为精机定位，定位动尺运动位移对应的对极数。感应绕组1的行波信号作为精机测量，测量对极内的位移量，两者组合实现绝对位移测量。

图8 实验平台Fig.8 Platform of the experiment

实验采用精度为±0.5×10-6的Renishaw激光干涉仪XL-80作为测量基准标定传感器。图9所示为传感器精机一个对极18 mm，气隙高度分别为0.1 mm、0.2 mm、0.3 mm的测量误差曲线，采用傅里叶变换进行分析，得到如图10所示的误差频谱图。实验数据表明：在对极内不同气隙高度对应的位移测量误差主要包含直流分量、一次谐波和四次谐波。当气隙高度d大于或小于0.2 mm时，直流分量和一次谐波呈增大趋势，而四次谐波则随气隙增大呈现不断减小趋势。实验结果与仿真结果相吻合，因此，采用气隙高度d为0.2 mm较合理。

图9 传感器不同气隙对极内的实测误差曲线Fig.9 Actual measurement error curves within a pole for different air gaps of the sensor

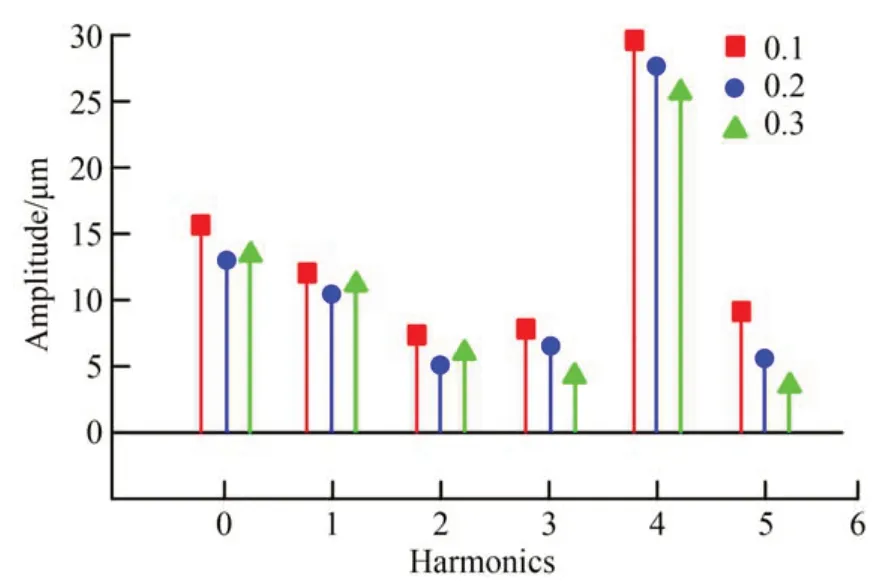
图10 不同气隙高度对应对极内实测误差频谱图Fig.10 Actual spectrogram of measurement error within a pole for different heights of air gap

图11所示为传感器精机一个对极18 mm内的测量误差曲线，分别对应感应绕组1沿正方向分别偏转0°、0.5°、1°时所得到的测量误差曲线。采用傅里叶变换进行分析，得到如图12所示的误差频谱图。实验数据表明：在无偏转时，测量误差谐波成分主要为四次谐波，偏转0.5°和1°时的谐波分量主要为直流分量和二次谐波，且幅值随偏转的角度增大而增大。在谐波分量中，四次谐波主要是由定尺绕组中正弦绕组和余弦绕组制造误差所引起的，而直流分量和二次谐波则是由于感应绕组安装时发生偏转引入的。

图11 精机极距内的测量误差Fig.11 Measurement error within a pole using multireaders

图12 精机极距内的误差频谱图Fig.12 Spectrogram of measurement error within a pole using multi-readers

整量程90 mm范围内，感应绕组1信号和感应绕组2信号组合后的精机定位误差如图13所示，修正前测量误差峰峰值为81.4μm，通过对对极内的测量误差曲线采用傅里叶谐波修正方法进行拟合修正［3］，修正后的测量误差峰峰值为5.7μm。由于感应绕组1对应的对极极距为18 mm，无论是原始测量误差还是修正后的测量误差都远小于对极极距，所以可以在量程范围内实现精机定位运动位移对极数。

图13 修正前后精机定位误差Fig.13 Positioning errors using multi-readers before and after compensation

整量程修正前后系统测量误差数据如图14所示，修正前原始测量误差的峰峰值为58.6μm，修正后的峰峰值为2.3μm。精机定位误差和精机测量误差主要由多对极绕组整量程的制造误差和传感器安装误差引起的，磁场互扰会引入一些高频谐波误差，后期可通过接地和屏蔽的方式加以改善。

图14 修正前后系统测量误差Fig.14 System measurement errors before and after error correction

绝对式时栅位移传感器的量程L为90 mm，由于激励绕组1和感应绕组1的对极数为5，激励信号频率为10 k Hz，而FPGA中进行插补的高频时钟脉冲频率为1.6 GHz，由式（10）计算得到该传感器的测量分辨力理论上可以达到0.1μm。并且，传感器精机测量的非线性最大偏差为30.1μm，满量程输出为90 mm，由式（11）计算整量程的原始测量线性度为0.033%。

实验采用精度为±0.5×10-6的Renishaw激光干涉仪XL-80作为测量基准标定传感器测量精度对传感器进行了三次重复定位精度实验，实验得到的测量误差如图15所示。实验结果表明：传感器在量程90 mm内的重复定位精度为±1.1μm。

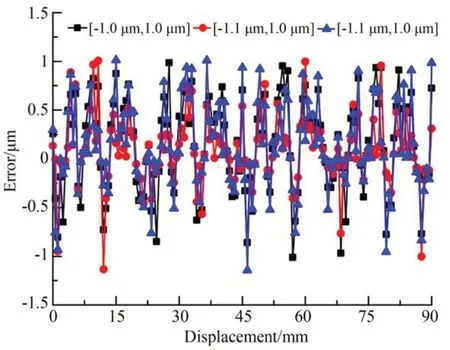
图15 传感器重复定位精度测量误差Fig.15 Measurement errors of sensor repeated positioning accuracy

5 结论

针对传统绝对式位移传感器复杂编码和严苛光刻加工的难题，本文提出了一种基于“精机定位+精机测量”技术的绝对式时栅位移测量新方法。利用“感应绕组面”实现对测量位移信号的精度调控。采用“精机定位+精机测量”多尺度组合测量技术构建大量程范围内的绝对位移测量模型。搭建实验平台进行精度实验，得出以下结论：

（1）传感器样机在90 mm范围内修正后的测量精度达到了±1.2μm，分辨力理论上可以达到0.1μm，重复定位精度达到了±1.1μm。研制的绝对式传感器与德国Heidenhain LC400系列和英国Renishaw FORTiS-N系列绝对式光栅技术指标对比如表1所示，研制的传感器不仅结构简单，还具有高精度、高分辨力的绝对位移测量优势。