基于RFID 载波相位的室内EKF 定位算法

谢良波，刘西西，王勇，周牧，田增山

（重庆邮电大学通信与信息工程学院，重庆 400065）

0 引言

随着物联网技术的快速发展，人们对室内环境中的智能应用和行为便捷要求越来越高，由于卫星信号在室内环境较弱，无法实现精确的室内定位，基于此，大量的室内定位技术被发现和研究。目前主要的室内定位技术主要有Wi-Fi[1]、蓝牙[2]、超声波[3]、红外线[4]、射频识别（RFID，radio frequency identification）技术[5]等。基于Wi-Fi 的室内定位技术是目前应用较多且相对成熟的技术，该技术利用与周围基站或者热点的最短距离信息确定目标位置。但是该方法受环境影响较大，稳健性较差，定位精度通常在米级。蓝牙定位通过接收信号强度指示（RSSI，received signal strength indication）求解目标的位置信息，主要应用于小范围定位，对于复杂的空间环境，其定位精度受噪声干扰的影响大。除此之外，超声波、红外线等技术都存在室内环境下定位精度差、只适合特定场合定位等缺陷。基于RFID的定位技术由于其非接触、非视距等优点有望成为优选的室内定位技术。该技术由已知位置的阅读器读取附着在物品或人员上的标签的特有的身份信息，进行定位或跟踪。RFID 标签体积小、成本低、通信效率高，一个读写器在1 s 内即可完成几百个标签的读写，在室内定位技术中具有重要研究意义。

在室内RFID 定位系统中，不管是静态定位还是动态跟踪及定位，在复杂的室内环境中实现厘米级精度都是一个很大的挑战。目前，基于RFID 的室内定位方法主要有基于RSSI[5]、基于到达角（AoA，angle of arrival）[6-7]以及基于载波相位[8-9]的定位方法。

其中，基于RSS 的定位方法利用接收到的信号强度进行距离估计，但是RSSI 信号在复杂的室内环境下衰减较快，受周围环境因素影响较大，定位精度较低。基于AoA 的定位方法对天线的间距和天线的数量有严格的限制，定位精度受设备的影响较大。基于此，众多学者提出联合定位算法。文献[10]利用天线的方向性，提出一种基于RSSI-AoA 的定位方法，但是该方法需要布置多个传感器来提高定位精度，并且系统性能受外界干扰影响较大。在此研究基础上，文献[10]提出引入MUSIC 算法来提高方向估计精度，从而在保证定位精度的前提下减少对传感器数量的依赖[11]。但是在实际应用中，噪声等干扰对测量的RSSI 值影响较大，MUSIC 算法不能减小或消除该影响，该方法与传统研究相比有效提高了方向估计精度但是定位精度仍然受不稳定RSSI 值的影响较大。

载波相位定位近年来成为研究人员的研究热点，载波相位与目标的位置信息高度相关，并且具有较好的噪声容忍度。文献[12]采用单个读写器天线和标签运动期间的多相位采样对门禁系统中的RFID 标签进行分类。文献[13]利用指纹对目标进行定位，并将基于相位指纹和基于RSSI 的指纹进行比较，结果显示相位指纹信息更加精确，但该方法的使用场景受到限制，只能应用到仓库或者零售店等特定场景中，不适用于一般室内场景。美国康奈尔大学的Ma 等[14-15]提出利用标签的非线性反向散射机制及接收信号的相位信息实现室内定位，但是整周模糊度解算复杂度高、计算量大、对设备要求较高。美国维拉诺瓦大学的Xin 等[16]提出了一种基于多频载波相位差的测距方法，并使用中国剩余定理（CRT，Chinese remainder theorem）估计各个频点卷叠相位值的隐含整周数，克服了相位周期模糊问题，但其定位精度受各频点相位误差影响较大。相比于传统基于RSSI 的RFID 室内定位方法，相位对时间和距离的变化十分敏感，具有更好的可行性，但是相位存在整周模糊问题，无法直接用于定位。

学者通常依据算法的准确度和计算量评价整周模糊度求解算法。目前常用的整周模糊度求解算法有最小二乘模糊度搜索算法[17]、优化Cholesky分解算法[18]、快速模糊度解算法[19]、LAMBDA（least-squares ambiguity decorrelation adjustment）算法[20-21]和CRT[14，16]等。其中，最小二乘模糊度搜索算法和快速模糊度解算法一般利用一个测量时刻的测量值或者短时间的观测信息求解整周，通过牺牲观测信息来达到快速搜索的目的，这类算法容易收敛至局部最小值，导致获得正确解的成功率不高。LAMBDA 算法在搜索算法中应用较多，有着较好的性能，但是该算法复杂度高，且容易受到测量值误差的影响，需要搜索空间足够大。除此之外，CRT 整周模糊度求解算法有很好的解整周效果，相比于其他解整周算法有更高的精度，但是该算法计算量大、算法复杂度高，需要建立一个高维的搜索矩阵，实时性不强。

针对上述问题，本文提出了一种基于跳频辅助的RFID 载波相位室内扩展卡尔曼滤波（EKF，extended Kalman filter）定位算法，实现了室内多径环境下厘米级定位。本文主要的研究工作如下。

1)提出一种应用于RFID 室内静态定位系统中基于RFID 载波相位室内的EKF 定位算法，利用双频下的多时刻相位信息完成厘米级定位，实时性比基于CRT 的定位算法提高了近10 倍。

2)提出一种基于多径抑制（MPS，multipath suppression）的双频点选择算法及EKF 参数优化算法。通过比较MPS 算法校正的相位与原始相位的绝对差值，选择差值最小的双频点用于EKF 解算。实验结果表明，MPS 辅助定位方法的平均定位精度比随机选择双频点的方法提高了23%左右。

1 定位系统架构及定位算法介绍

1.1 系统架构

定位系统架构如图1 所示，其包含阅读器、无源RFID 标签、激励器、接收天线、外部时钟源和定位服务器。其中，阅读器发射低功率信号f1用于与标签通信。标签用于反射并调制自身的电子产品代码（EPC，electronic product code）。激励器发射高功率信号f2用于激活无源标签并在定位服务器控制下同步跳频。接收天线用于接收信号。外部时钟源用于实现多台收发设备的时钟同步和时间同步。定位服务器用于控制阅读器和跳频系统，并对数据进行存储和处理，实现测距和定位。

1.2 传统CRT 联合聚类定位算法

由于载波相位存在周期性，对于采集到的K个频点下的相位，可建立距离方程为

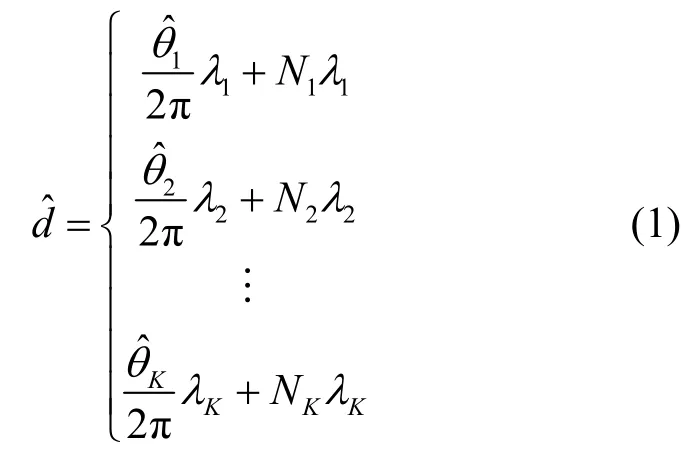
其中，为解整周之后的相对距离估计值，为第K个频点下的相对相位值，λK为第K个频点对应的波长，NK为整周数。由式(1)可知，该欠定方程存在无数个解。此时，采用聚类算法对整周数进行遍历搜索，根据测量范围设置最大的迭代整周数为

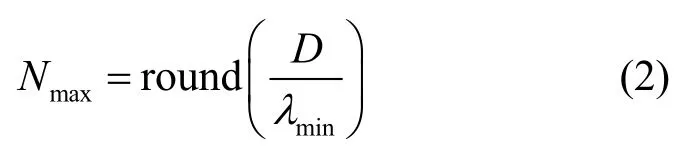
其中，D为测量范围的最大距离，λmin为最大频率对应的最小波长，round(x)为对x值四舍五入取整。则可得一个K×Nmax的距离搜索矩阵，如图2 所示，对距离方差最小的一列取均值作为相对距离估计值。

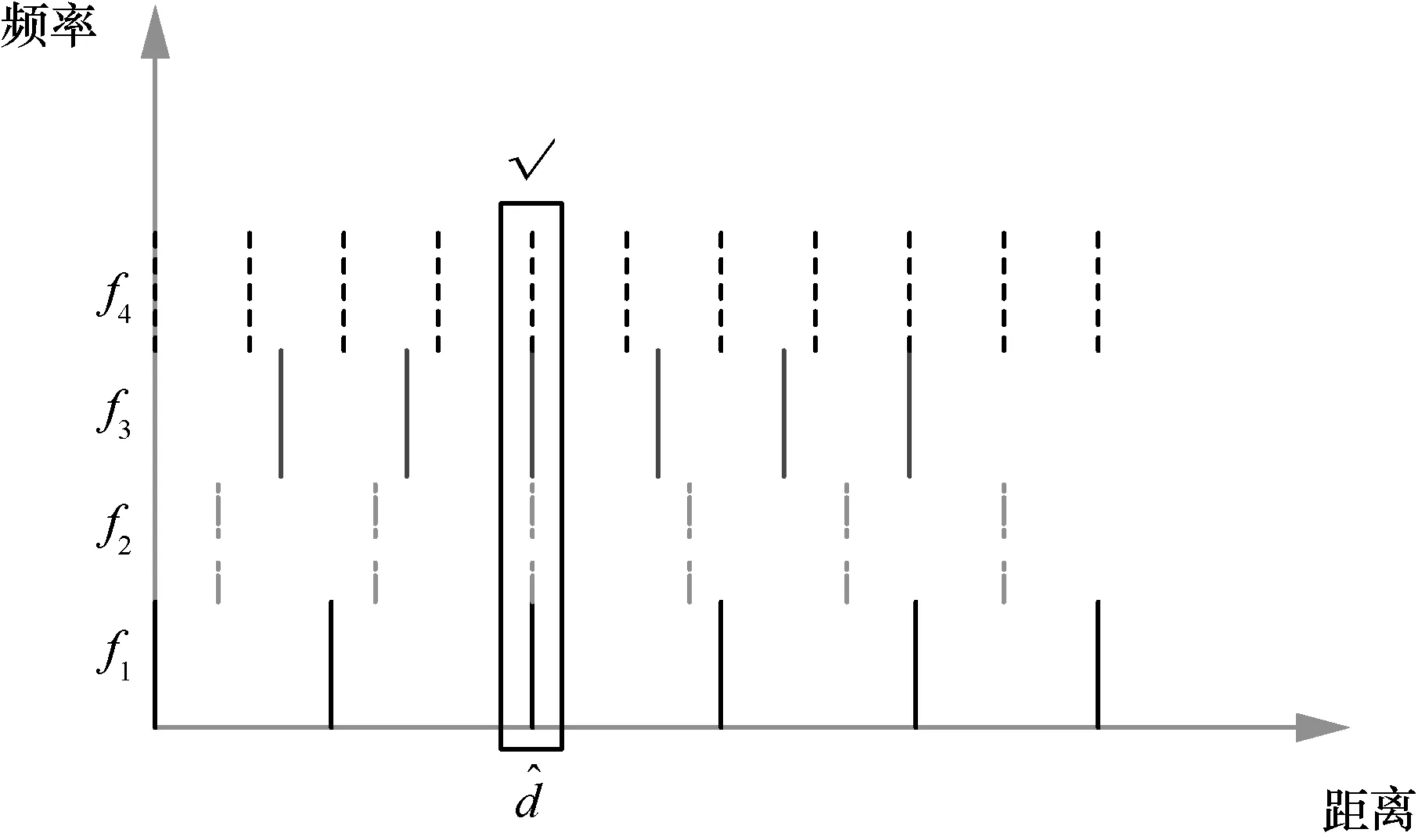
图2 CRT 解整周原理

结合式(1)求得待测点链路总距离为

其中，dref为参考标签链路总距离。联合式(3)待测点链路总距离，利用椭圆定位算法实现目标定位[22]。

然而，该方法需要联合多个频点下的相位信息，且各频点相位的误差对测距精度影响较大，从而影响整体定位精度。除此之外，该算法复杂度高，需要建立一个高维搜索矩阵，耗费时间长，不具有实时性。针对该问题，本文提出在基于载波相位的RFID 跳频系统中利用基于双频点的扩展卡尔曼滤波的方法进行整周模糊度解算，在保证定位精度的前提下，降低算法复杂度，提高定位实时性。

1.3 基于RFID 载波相位的EKF 定位算法流程

为了解决传统CRT 联合聚类定位算法复杂度高、实时性较差、多频点相位误差对精度影响较大等问题，本文提出基于RFID 载波相位的室内EKF定位算法。算法流程如图3 所示。

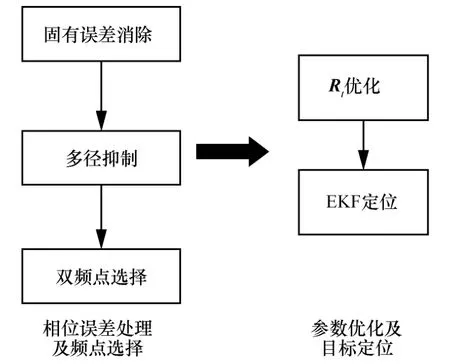
图3 定位算法流程

定位算法主要包括相位误差处理及频点选择、参数优化及目标定位两部分。其中，相位误差处理主要是对设备产生的固有相位误差以及多径引入的相位误差进行抑制或消除。固有相位误差主要是通过设定标定点进行消除，多径引入的相位误差采用MPS 算法进行抑制。此外，本文采用的基于RFID载波相位的EKF 定位算法仅仅需要双频点，所以利用MPS 辅助滤波算法选择可靠的双频点，并采用双频点相位下的多时刻相位值对测量误差协方差矩阵R进行跟踪优化，最终用于EKF 整周解算及定位。与CRT 算法相比，所提算法实时性强，极大地降低了算法的复杂度，并有效提高了定位精度。

2 相位误差处理及频点选择

2.1 固有相位误差消除

标签反射信号经过I/Q 正交解调以及低通滤波器滤除高频分量，得到同向和正交2 个支路信号，则信道的CFR 为

其中，I和Q分别为同向和正交2 个支路信号。接收到的相位为

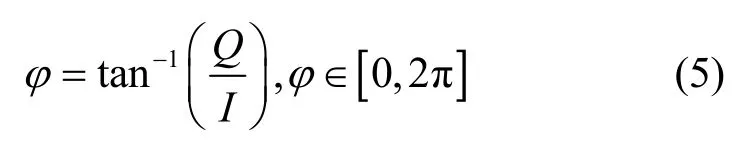
由于跳频范围内部分频点离标签天线最佳匹配频段较远，且存在频率选择性衰落的影响，对数据的接收产生了干扰。为了减少上述因素对接收数据的影响，首先对相位进行预处理，主要包括相位解卷绕和奇异值剔除两部分，经过预处理过程后的相位为θ。

相位存在2π 翻转现象如图4 所示。其中，频率为780 MHz。用于本文频点选择算法的每个频点下的相位均是多轮次相位取均值，因此利用某轮数据直接取均值，均值相位在0 rad 附近，会造成很大的相位误差，因此本文对相位数据进行解卷绕处理后再求均值。解卷绕是指使相位在 -π和π 处不发生跳变，从而反映真实的相位变化。

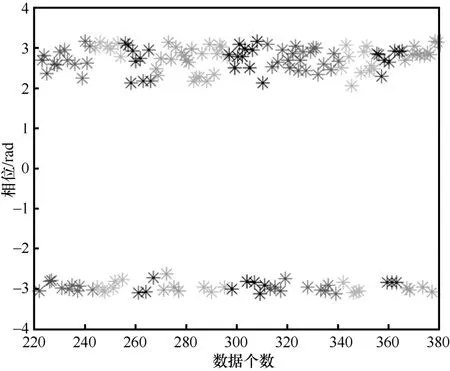
图4 相位存在2π 翻转

相位存在奇异值现象如图5 所示。其中，频率为840 MHz。大部分频点的相位数据在随时间累积的过程中是稳定的，但是会出现极个别的异常值。由于用于多径抑制算法和双频点选择算法的相位为频点的均值相位，异常值的存在会影响数据的统计特性，因此需要剔除异常值获得更准确的均值相位。本文利用3σ准则（3 倍标准差准则）来剔除数据中的奇异值。

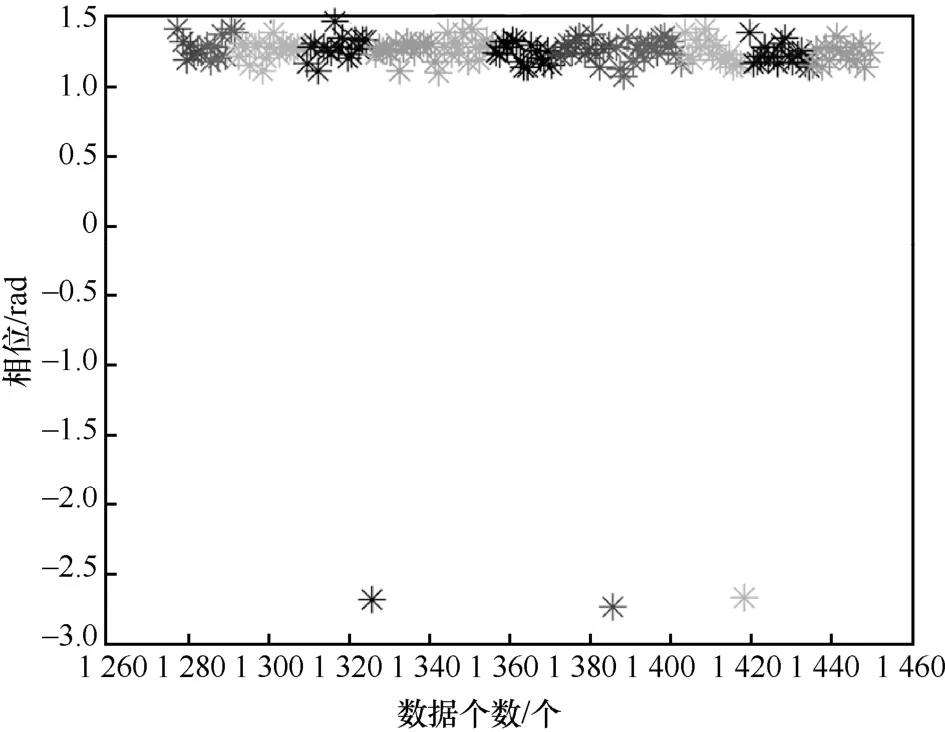
图5 相位存在奇异值

由于收发设备和环境等因素，接收信号会引入误差，影响相位的精度和可靠性，因此经过预处理过程后的相位可表示为

其中，θτ为发送信号飞行时间（ToF，time of flight）累积相位，θ0为初始相位偏移，θc为载波频率偏移（CFO，carrier frequency offset），θH为收发设备造成的固有相位偏移，θn为多径和环境噪声引起的相位误差。在RFID 系统中，标签采用反向散射机制，可对载波信号实现无差别的调制，标签自身不会引入CFO。因此，θ0和θc可通过对RFID 发射端和接收端的时钟源同步进行消除。

综上，如何消除收发设备造成的固有相位偏移θH及多径和环境噪声引起的相位偏移θn是减小相位误差的关键。对于设备造成的固有相位偏移，本文采用目标标签与参考标签之间的到达相位差（PDoA，phase difference of arrival）的方式进行测距和定位。

假设第n个接收天线接收到的K个频点下参考标签的相位为，目标标签的相位为，因为接收到的相位表示标签所在位置信号整个传播过程的链路总距离，通过目标标签相位与参考标签相位之差来消除固有相位误差，对应的相对相位值为

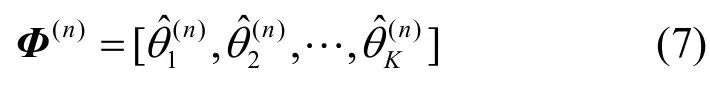
为了消除相位固有误差，利用待测点相位和参考点相位之差进行目标位置解算，即表示相对相位，利用相对相位进行距离解算，即表示相对距离。利用该相位值进行相对距离估计和定位，由于参考标签位置已知，即可得到目标标签的绝对距离和真实坐标。

综上，θH可采用设置参考标签，通过目标标签的相位与参考标签相位差分进行消除。对于多径和环境噪声引起的相位误差θn，本文采用MPS 算法进行抑制。

2.2 基于MPS 辅助的双频点选择算法

根据式(7)可得经过参考标签校正后第n台接收机对应的K个频点下的相对相位，并利用该相位重构CFR，即

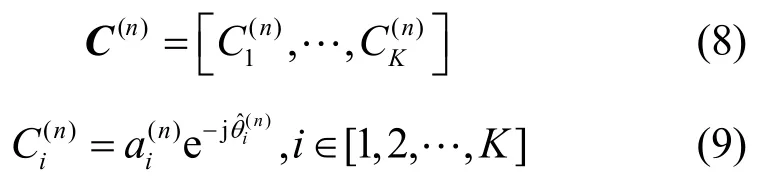
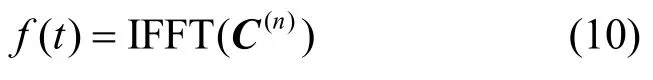
时域信息波形图峰值对应的时间τ即信号传播的最短路径的飞行时间，根据该飞行时间可得待测目标所在位置相对距离粗估计值为

其中，光速c=3 ×108m/s。傅里叶逆变换后的时域波形如图6 所示。由于室内多径、环境噪声等因素，接收端接收的信号是包括多径信息和环境噪声在内的多个信号的叠加，导致傅里叶逆变换后的时域波形峰值受多径影响产生时延，粗估计距离误差较大，无法实现高精度定位。

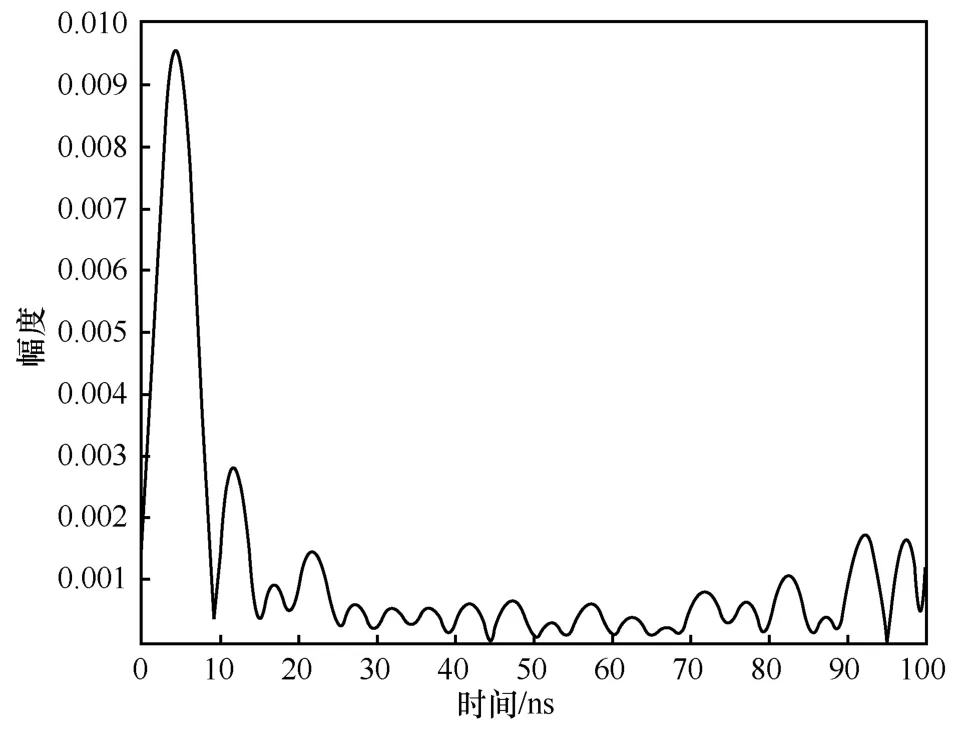
图6 傅里叶逆变换后的时域波形

假设有L条多径，则由式(9)可得第n个接收天线对应频率fi经过参考点校正的CFR 为

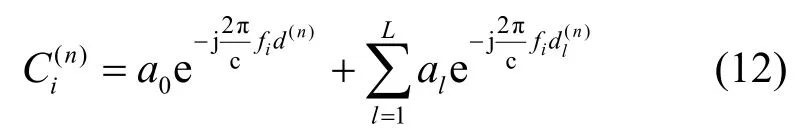
其中，a0和al分别为视距（LoS，line of sight）路径的信号幅度和第l条路径的信号幅度，d(n)和分别为LoS 路径的真实距离和第l条路径的真实距离。

以式(11)得到的距离粗估计值对各频点的相位进行处理，可抑制多径效应对LoS 信号的影响，得到多径抑制后的相位测量值为

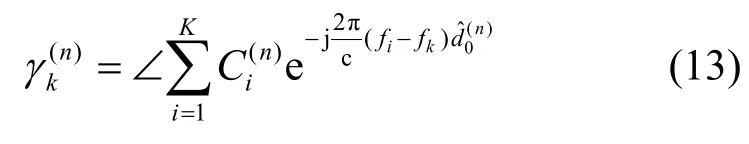
其中，∠为取角符号。

将式(12)代入式(13)可得

从式(14)和式(16)可以看出，由式(13)处理后，可达到突出LoS 抑制多径的效果，即由式(13)得到的相位在较大程度上抑制了多径效应的影响。采用多径抑制后的相位来筛选可靠的双频点作为EKF定位算法的输入，以提高定位精度。MPS 算法处理前后的相位对比如图7 所示。从图7 可知，与多径抑制前相位相比，MPS 算法处理后的相位误差大大减小。由此，本文提出了一种基于MPS 辅助的双频点选择算法，筛选用于EKF 定位算法的双频点，即

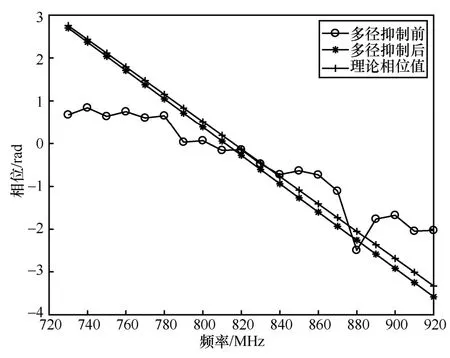
图7 MPS 算法处理前后相位对比

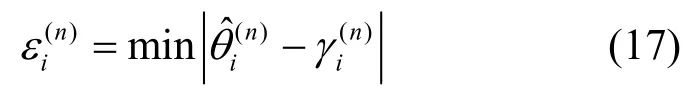
3 EKF 定位算法

假设待测标签坐标为T=(x，y)，发射天线坐标为TX=(x0，y0)，第n个接收天线坐标为，本文为了消除设备带来的固有误差，对每个接收天线均设置一个参考标签，因此第n个接收天线对应的参考标签的坐标为

3.1 状态方程的建立

假设用于 EKF 算法的双频点为i1，i2∈[1，2，…，K]，选取状态变量为

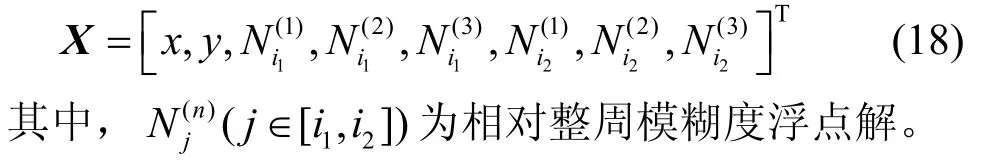
卡尔曼滤波算法通常被用于估计整周模糊度的浮点解，根据初值和观测值进行更新迭代[22]。在静态环境中，状态转移矩阵不随时间变化而变化，而在动态环境中，状态转移矩阵通常随时间变化而发生改变。在本文系统中，对无源静态标签进行定位，状态转移矩阵为单位矩阵并且不随时间发生变化，因此状态转移矩阵U为单位矩阵，因此t时刻下系统的状态方程为

应用EKF 算法进行迭代更新，需要对式(19)设置初始状态变量，即

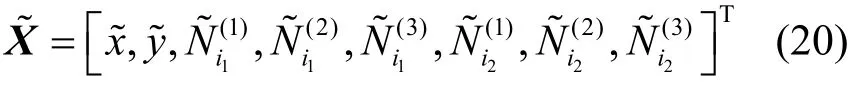
3.2 量测方程的建立及其线性化

假设对无源标签进行二维定位，采用一发三收系统。则构建量测方程为

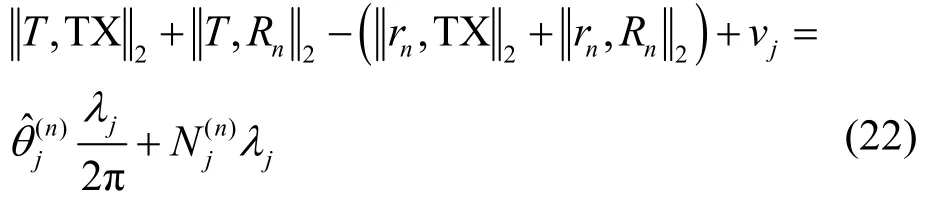
将式(22)中的待求参数移至方程左边可得

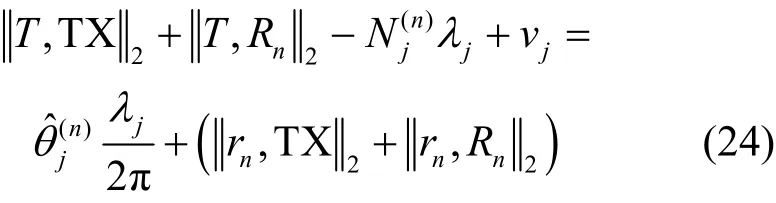
根据式(24)，定义不同接收天线不同频点下的系统观测模型为

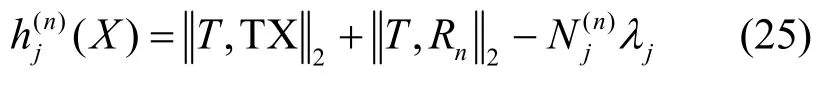
在本文定位模型中，采用一发三收系统，且EKF 的输入为双频点，因此EKF 定位模型下的系统观测模型为

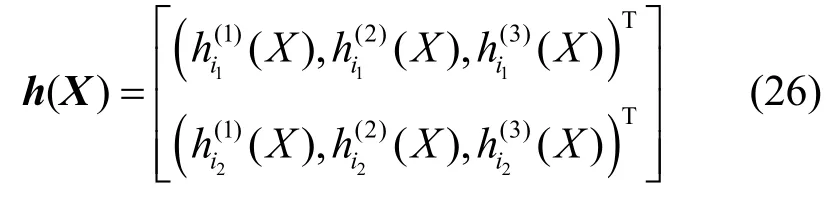
由于式(25)为非线性观测模型，采用泰勒展开的方法并忽略二次及以上项对式(25)线性化，结合式(20)，可得基于载波相位的观测模型为

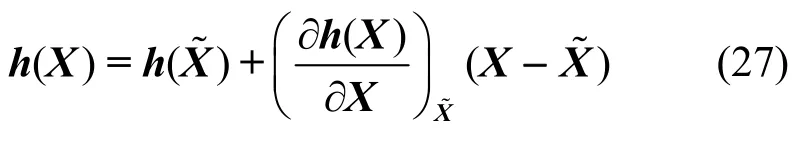
则线性化后的观测模型为

I3和O3分别为3 维单位矩阵和3 维零矩阵。

根据式(24)可得基于载波相位的观测量为

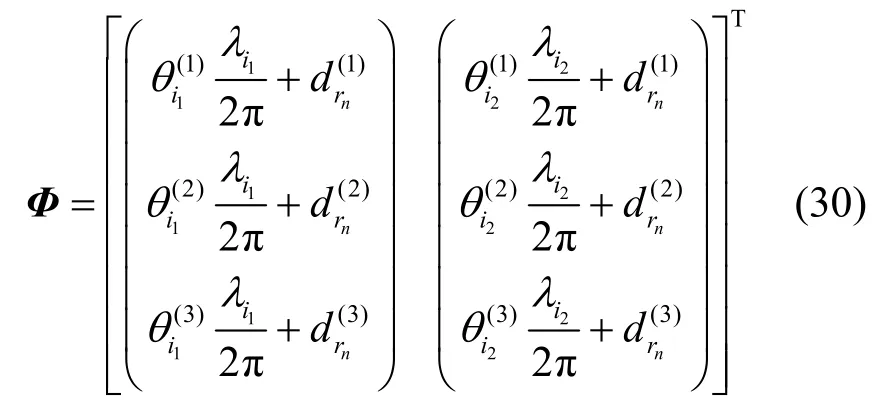
由式(11)和式(23)可得基于距离的观测量为

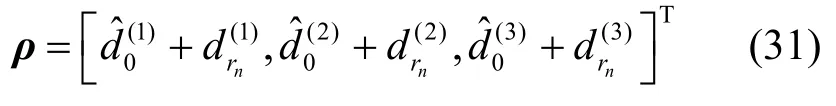
在本文系统中，将载波相位和距离粗估计联合作为观测值，联合式(22)、式(30)和式(31)可得系统观测矩阵为

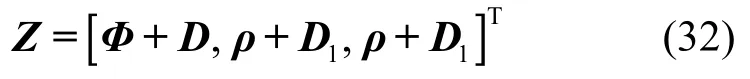
其中，D和D1均为常数矩阵。根据式(24)，令待测位置对应3 个接收天线的链路总距离矩阵表示为

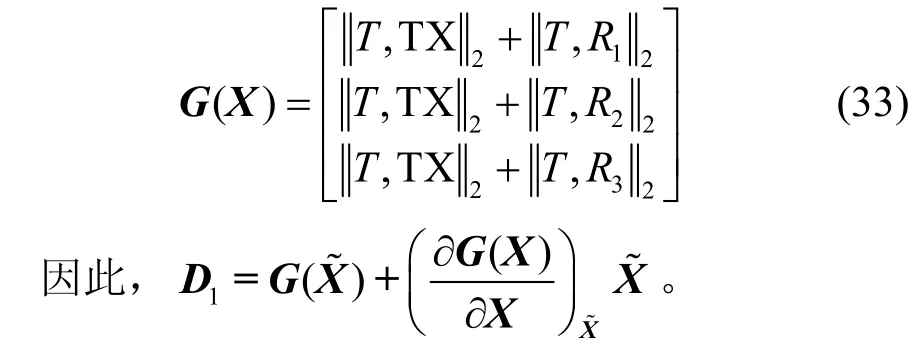
根据式(22)和式(28)可得系统的测量关系矩阵为

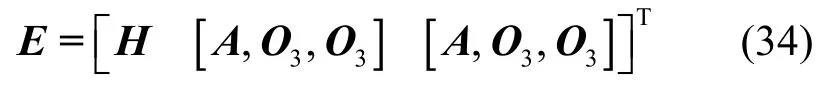
由式(19)、式(28)和式(34)可得线性化后的量测方程为

其中，Vt表示t时刻下的测量噪声矩阵。

本文系统中，利用跳频系统获取了多频点下不同时刻的相位信息。假设t时刻的观测值为Zt，t-1时刻的状态变量Xt-1的最优估计为，利用选取的双频点下的不同时刻相位信息完成Xt的最优估计。滤波过程如下。

首先，根据初始状态变量进行状态先验估计

然后，进行状态预测

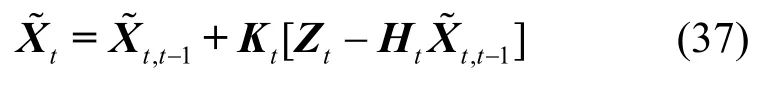
其中，卡尔曼增益矩阵为

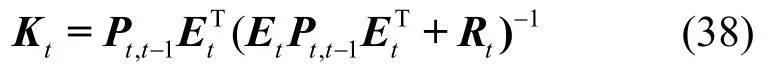
其中，Rt为测量误差协方差矩阵。

先验估计误差的状态均方误差阵为

因此，后验估计误差的状态均方误差阵为

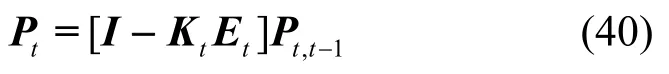
综上，通过设置初始估计值和P0，根据t时刻的观测值Zt，就可以得到t时刻的状态估计(t=1，2，…)。

3.3 EKF 参数优化

由于噪声向量是未知的，并且协方差矩阵Rt会随着时间的不同而发生变化，在定位过程中为了简化计算，通常设置Rt为常系数矩阵。对于本文定位系统，待测目标在同一位置不同时刻下的载波相位观测值理论上是一个定值，但实际上由于环境和收发设备的影响，载波相位会产生波动。在840 MHz下同一位置的不同时刻接收相位值如图8 所示。若按照如图8中不同时刻下的所有相位值进行卡尔曼更新迭代，并且设置Rt为常量矩阵，会极大地影响卡尔曼滤波结果。

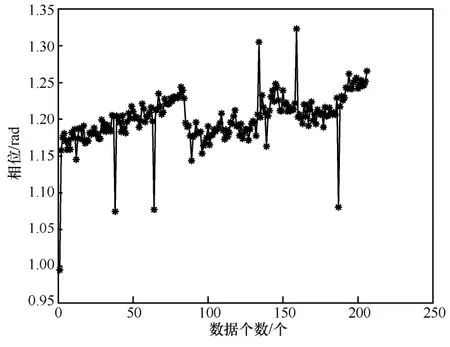
图8840 MHz 下同一位置的不同时刻接收相位值

根据式(38)可知，Rt相当于是对载波相位观测值准确度设置的一个权值，通过设置Rt值来衡量不同时刻下相位值的可信度。理想情况下，在同一位置同一频点下，对同一接收天线，其相位值相同，是一条水平直线。因此，根据式(17)得到可靠频点，结合式(13)中可靠频点下多径抑制后相位(j∈i1，i2∈[1，2，…，K])对Rt进行优化可得

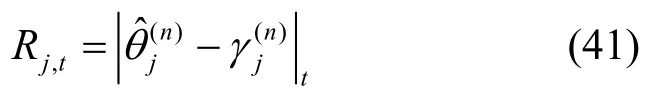
由式(38)可知，Rt值随着测量误差增大而增大，而Kt随着Rt值增大而减小，通过优化Rt值实时监控测量误差可以有效提高定位精度。

4 实测实验与结果分析

4.1 测试平台

为了验证本文所提定位系统的性能，搭建了如图9 所示的测试场景，测试环境为普通室内环境，测试范围为4m ×4m，发射天线的坐标为（45 cm，75 cm），3 个接收天线R1、R2、R3的坐标分别为（35 cm，0）、（35 cm，75 cm）、（35 cm，150 cm），标定点的坐标分别为（150 cm，0）、（150 cm，75 cm）、（150 cm，150 cm）。测试所用跳频范围为780～900 MHz，跳频间隔为10 MHz。每个频点均采集了200～300 个时刻下的相位信息。

图9 测试场景

图10 为模拟测试环境，本文采用一发三收定位系统，发射和接收天线均采用波瓣宽度为120°的圆极化天线，图10中扇形区域为接收天线R1的辐射范围。假设标签定位区域分为3 个区域，分别为D1，D2，D3。测试环境中有严重的多径现象，图10中只标出了经标签反射的不同接收天线接收的LoS 信号传播路径。测试实验所用设备以及用途如表1 所示。

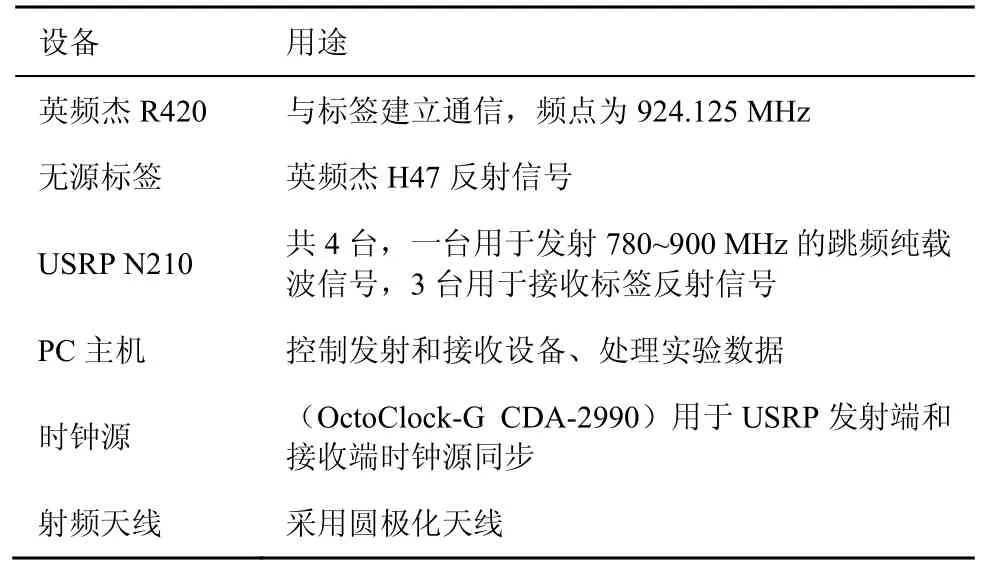
表1 测试实验所用设备以及用途

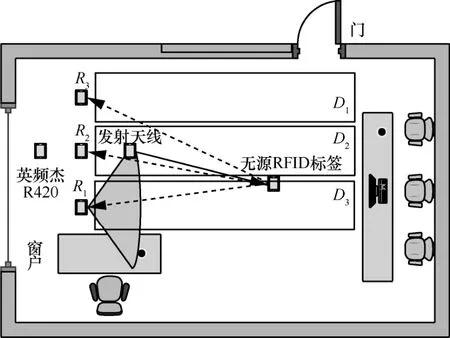
图10 模拟测试环境

4.2 不同算法定位精度比较

本文选取传统的基于多频点的CRT 算法[16（]选取20 个频点用于定位）、MPS+CRT 算法[14]（选取20 个频点用于定位）与本文算法（选取2 个频点用于定位）进行对比分析。

图11 为不同定位算法定位误差累积分布。从图11可以看出，本文算法的平均定位误差为9.35 cm，传统CRT 算法平均定位误差为22.09 cm，MPS+CRT定位算法平均定位误差为12.06 cm。可见，本文算法定位精度要优于CRT 算法，主要原因是CRT 算法利用多个频点联合进行定位，受到各频点相位误差的影响；并且由于环境影响，某些频点易产生丢包现象，导致频点缺失或者该频点下接收相位数据极少，相位误差较大，因此CRT 算法对整个系统要求较高。

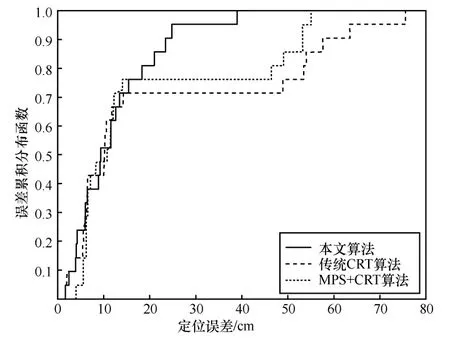
图11 不同定位算法定位误差累积分布

图12 为MPS+CRT 算法采用不同频点数量时定位误差累积分布。采用20 个、15 个、10 个和5 个频点时的平均定位误差分别为12.06 cm，31.78 cm，63.92 cm和87.35 cm。尽管MPS+CRT 算法在20 个频点时的平均定位误差可达12.06 cm，但其定位实时性不高（见4.6 节）；减少频点的数量可以提高实时性，但是定位精度会降低。

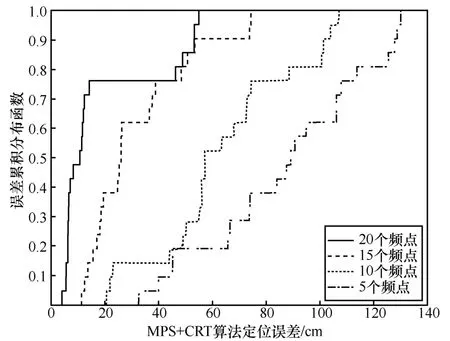
图12 MPS+CRT 算法采用不同频点数量时定位误差累积分布

4.3 EKF 算法优化性能分析

由于本文所提EKF 定位算法只需要2 个频点下的相位信息进行定位，因此对这2 个频点的可靠性要求较高。本文采用基于MPS 辅助的双频点选择算法完成可靠双频点选取，并对Rt值进行了优化。图13为EKF 算法进行频点优化（即可靠双频点选取）前后和Rt值优化前后定位误差累积分布。其中，优化前随机选择双频点进行EKF 定位，并将Rt值设为常量。从图13 可以看出，对频点和Rt值均进行优化后的平均定位误差为9.35 cm，只进行频点优化，Rt值设为常量的平均定位误差为15.92 cm，不对参数进行优化的平均定位误差为23.28 cm。因此，本文提出的双频点选择算法及Rt值参数优化可有效提高定位精度。

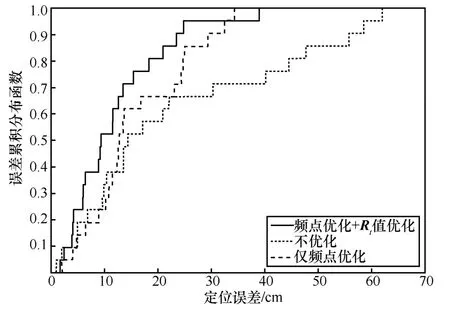
图13 EKF 算法优化前后定位误差累积分布

4.4 不同接收天线测距精度比较

测距精度会影响定位精度，图14 为EKF 算法下不同接收天线测距误差累积分布。接收天线R1的平均测距误差为8.33 cm，接收天线R2的平均测距误差为8.15 cm，接收天线R3的平均测距误差为8.42 cm。显然，R2的测距精度要高于其他接收天线，主要原因是本文所采用的接收天线是波瓣宽度为120°的圆极化天线，所以R1和R3的覆盖范围比R2小，最终导致对测量区域两边的目标标签进行测距时精度较R2低。

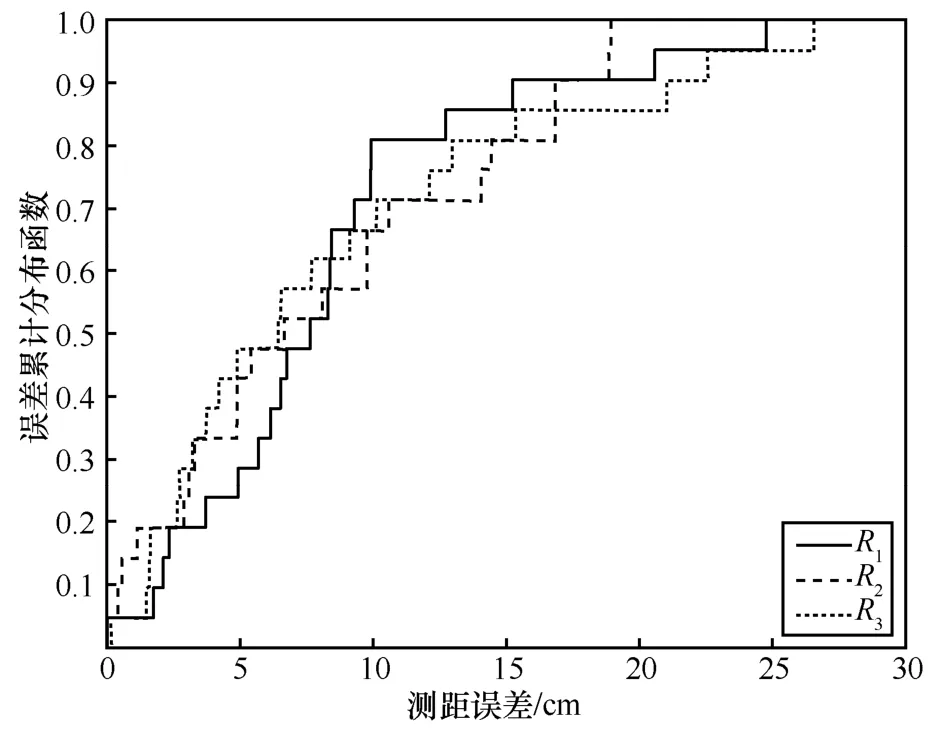
图14 EKF 算法下不同接收天线测距误差累积分布

4.5 标签摆放位置定位精度比较

由于天线的方向性和环境中多径效应等因素的影响，标签在不同位置定位精度存在差异。本文采用的天线是波瓣宽度为120°的圆极化天线，导致接收天线R1和接收天线R3对定位区域D3和D1中的部分标签定位精度产生交叉影响。图15 为不同区域的定位误差累积分布。从图15 可知，由于3 个接收天线能够较好地接收到中间区域的标签反向散射信号，因此定位区域D2定位精度最高，区域D1相比于区域D3定位精度差，原因是环境中区域D1旁边存在桌子等杂物，多径现象较严重。

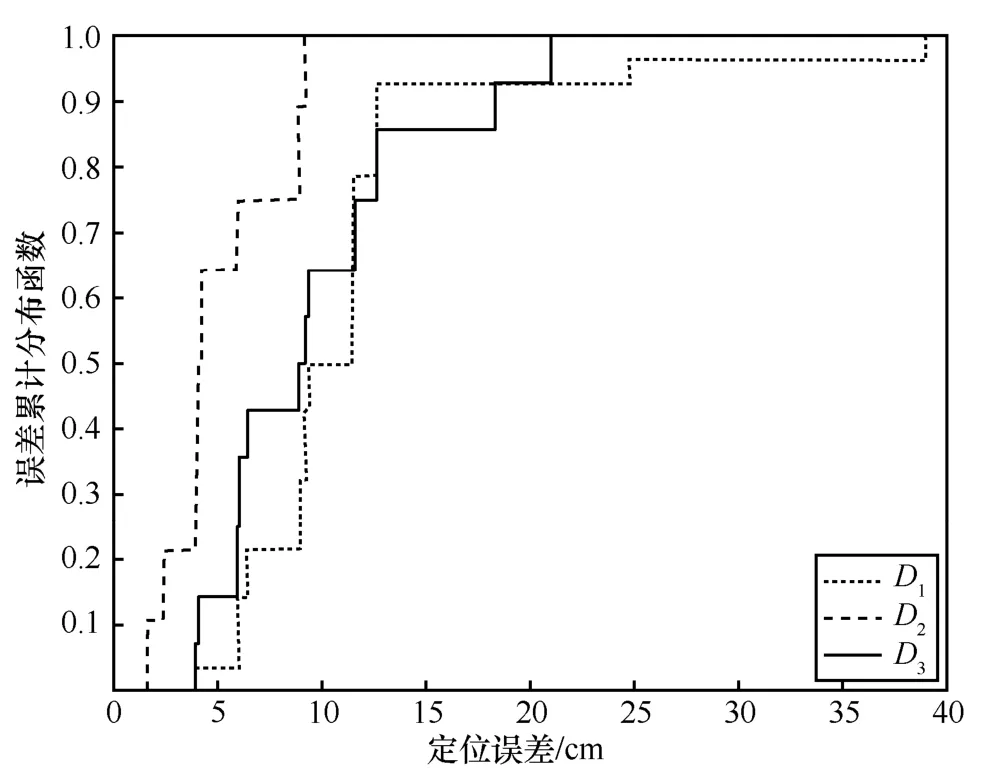
图15 不同区域的定位误差累积分布

4.6 实时性分析

实时定位是实现室内高精度定位的一个难点。本节主要对传统CRT 算法、MPS+CRT 算法和本文算法实时性进行对比分析。图16 为不同算法实时性对比结果。从图16 可知，对单个位置进行解算时，本文算法、传统CRT 算法和MPS+CRT 算法所需时间分别为0.43 s、4.35 s和5.37 s；解算10 个位置时，所需时间分别为4.23 s、42.85 s和51.85 s；解算20 个位置时，所需时间分别为8.72 s、88.04 s和97.83 s。因此，本文所提算法定位效率比其他2 种算法提高了近10 倍，实时性较高。

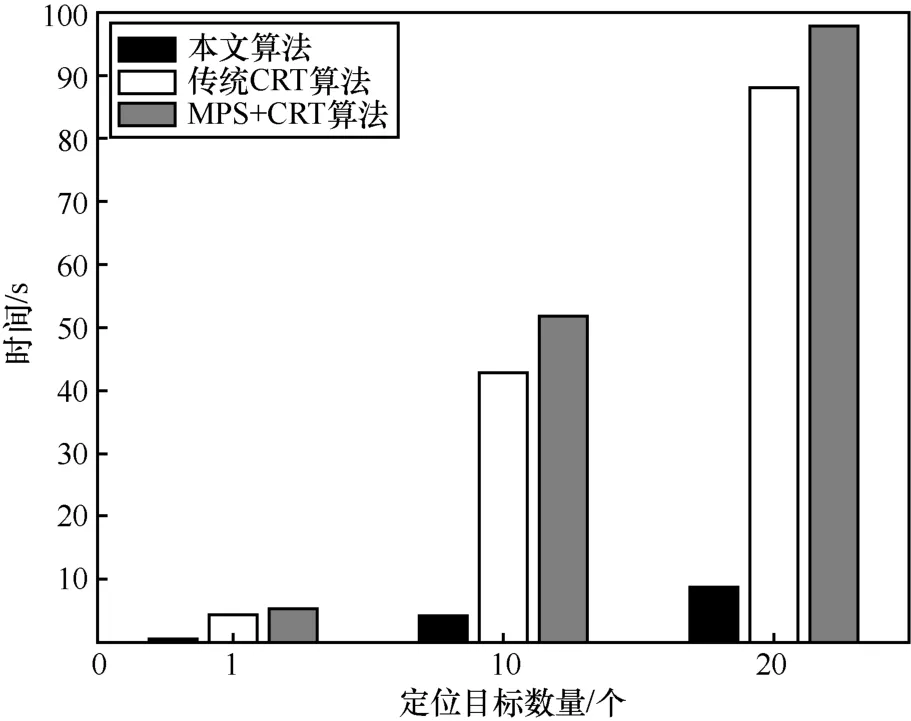
图16 不同算法定位实时性对比

5 结束语

本文提出了一种基于RFID 载波相位的室内EKF 定位算法。通过跳频技术获取虚拟大带宽实现距离粗估计，并以粗估计距离对相位进行处理，实现多径抑制；在此基础上，提出了一种基于MPS辅助的双频点选择算法及EKF 参数优化算法。最后，根据选取的双频点下多时刻相位信息，利用EKF 算法进行整周模糊度解算，最终实现定位。实验结果表明，本文所提算法的平均定位误差为9.35 cm，并有效降低了算法复杂度。