多载波NOMA 安全通信系统稳健性资源分配算法

张钰，赵雄文，王晓晴，耿绥燕，秦鹏，周振宇

（1.华北电力大学新能源电力系统国家重点实验室，北京 102206；2.华北电力大学河北省电力物联网技术重点实验室，河北 保定 071003）

0 引言

随着5G 通信技术的发展和网络的建设，面向海量终端业务接入的5G 物联网将应用到工业和人们的日常生活中[1-2]。在该背景下，如何充分利用有限频谱资源扩大网络连接以及如何提升网络信息传输的安全性和隐私性是无线通信系统需要考虑的关键问题。近年来，非正交多址接入（NOMA，non-orthogonal multiple access）[3-4]允许在同一时频资源块上服务多个用户，成倍提升系统容量，受到人们广泛关注。基于人工噪声（AN，artificial noise）的物理层安全（PLS，physical layer security）技术[5-6]提供了一种轻量级安全通信手段，以信息论为基础，利用无线信道的物理层特性实现信息安全传输，不需要依赖复杂的加密解密算法。因此，基于物理层安全的NOMA 系统可实现提升信息安全性、提高频谱效率和扩大网络连接的目标，成为工业界和学术界关注的热点。

NOMA 通过在发送端进行功率叠加编码，在接收机利用连续干扰消除（SIC，successive interference cancellation）技术来避免同道干扰，从而获取期望信号[7]。关于单载波NOMA 系统中资源配置与优化的研究已取得较大进展，而针对多载波NOMA 系统的研究相对较少。文献[8-9]分别针对存在2 个用户的下行和上行单载波NOMA 系统，以最大化系统可达和速率为目标提出了功率分配和预编码矢量联合优化算法。文献[4，10]针对存在多用户（2 个以上）的单载波NOMA 系统，分别以最大化频效和能效为目标，对基站预编码和用户功率分配方案进行了研究。单载波NOMA 系统中，所有用户占用同一信道，彼此之间同频干扰严重，多载波NOMA 系统中用户被分配到不同的信道，不同信道上的用户彼此间不会产生同频干扰，但子载波分配策略会对系统性能产生显著的影响。文献[11]研究发现将信道增益差别较大的2 个用户分配到同一子载波上有助于改善系统性能。文献[12-13]假设基站和用户都是单天线，对子载波和功率分配算法进行了优化设计。实际无线通信系统都是多载波系统，且多载波NOMA 技术具备更高的资源配置灵活性，因此研究多载波NOMA 系统更有意义。

PLS 技术在NOMA 系统中的应用尚处于初步研究阶段。近年来，文献[14]考虑存在一个单天线窃听者（Eve，eavesdropper）的下行NOMA 网络，假设基站能够获取完美的合法和窃听信道状态信息（CSI，channel state information），建立了以最大化安全能效为目标的功率优化问题，同时满足基站最大发射功率和用户数据传输速率限制，并采用一阶泰勒展开和连续凸逼近算法求解。文献[15]考虑基站发射AN 对Eve 进行干扰，假设窃听信道CSI未知，提出了下行数据及AN 预编码矢量优化算法，以最大化AN 发射功率的同时满足基站最大发射功率和用户数据传输速率约束。文献[16]假设窃听信道非完美CSI，分析了多天线下行NOMA 系统安全中断概率。与单载波系统不同，多载波NOMA 网络中子载波分配与预编码矩阵和人工噪声等优化变量紧密耦合，导致资源分配问题中待优化变量增多，求解难度增大，因此文献[14-16]所提资源分配算法不能直接应用于多载波系统。目前针对PLS 在多载波NOMA 系统中的应用研究较少，文献[17]以最大化安全和速率为目标对上行NOMA 系统中功率和子载波分配进行联合优化，文献[18]以最大化安全能效为目标，对放大转发的双向中继NOMA网络中功率和子载波分配进行联合优化。上述工作都是针对单天线系统，不涉及预编码矢量的优化，所提算法不能直接用于求解多天线系统的资源分配问题。

针对上述问题，本文研究多载波下行多天线NOMA 安全传输系统AN 预编码矢量、数据预编码矢量以及子载波分配的联合优化，主要的研究工作如下。

1)建立下行多载波NOMA 安全通信网络资源分配模型。首先，设计AN 预编码矢量与合法用户信道正交，消除AN 对合法用户信号的干扰。随后，以最大化合法用户的安全和速率为目标，对下行数据信号和AN 的预编码矢量以及子载波分配策略进行优化，满足最小速率和最大发射功率约束。考虑窃听信道不确定性的影响，建立非理想CSI 情况下的稳健性资源分配问题。本文所建立的优化模型是一个非凸、非线性、多变量耦合的优化问题，很难直接获得解析解。与单载波系统优化问题相比，本文模型增加了子载波分配，不同分配方案将导致优化问题的目标函数及限制条件的表达式发生变化，求解难度更大。

2)提出了稳健性资源分配算法。将原始问题分解为预编码优化和子载波分配2 个子优化问题，利用S-procedure 算法[19]将预编码矢量优化问题中含不确定性参数的目标函数转换为确定性形式，再利用块坐标下降（BCD，block coordinate descent）算法求解；利用动态匹配理论[20]将子载波分配问题重新定义为双边匹配问题，并采用延迟接受（DA，deferred acceptance）算法[21]求解；同时给出了本文的算法步骤、计算复杂度分析。多载波系统资源分配算法[12-13]没有考虑信息传输的安全性，文献[17-18]算法只适用于单天线系统，且只能对功率和子载波2 种资源进行优化配置，本文所提算法适用于多天线系统，且能够实现AN、数据预编码矢量（包含功率）、子载波多种资源的联合优化。

3)研究结果表明，本文所提方案具有很好的稳健性，与传统OMA 传输以及其他文献中先进方案相比，能有效提高系统安全和速率。所提子载波分配算法性能与穷尽搜索算法性能非常接近，但计算复杂度显著降低。

1 系统模型

1.1 信号分析

存在窃听者的下行多载波NOMA 系统模型如图1所示，下行多载波NOMA 通信系统中存在一个多天线基站、K个合法用户和一个多天线Eve。基站为合法用户提供数据服务的同时需要额外发送一个AN信号，以降低窃听信道的质量，提高信息传输的安全性。假设所有合法用户配置单根天线，基站和Eve分别配置M和N根天线，且M＞N[22]。为避免用户之间过强的共道干扰并降低接收机SIC 复杂度，网络中可用带宽B被均分为I个带宽为的子载波，每个子载波上只允许存在2 个用户同时工作。定义和分别表示子载波集合和分配在子载波Ci上的用户集合。基站的发射信号可表示为

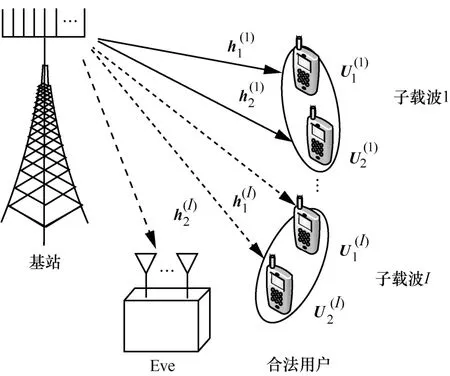
图1 存在窃听者的下行多载波NOMA 系统模型

1.2 数据速率

本节基于图1 所示系统模型，推导网络整体安全和速率表达式，作为第2 节数学优化问题中的目标函数。以子载波Ci为例，根据NOMA 原理，信道增益较强的用户能解码出信道增益较弱用户的信号，并将其从接收信号中剔除，假设，则强用户接收机处SIC 的解码顺序遵循

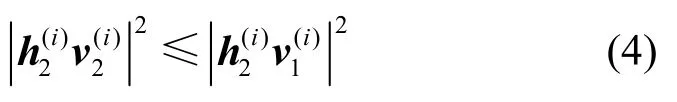
合法用户数据传输速率为

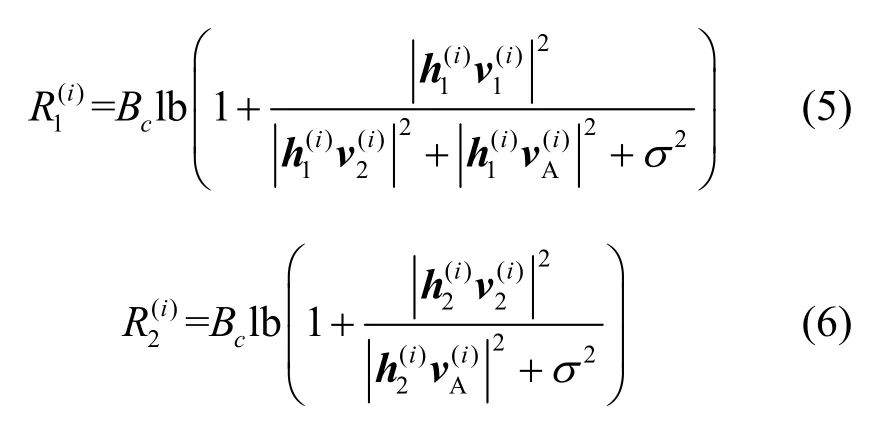
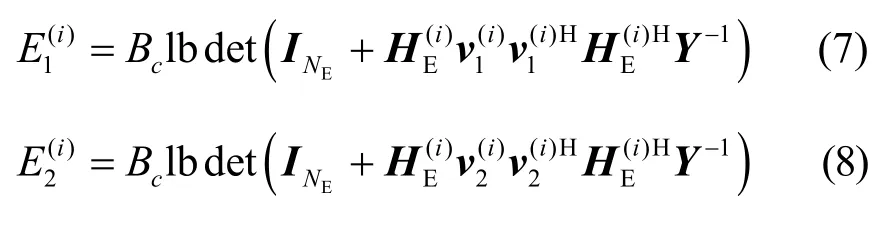
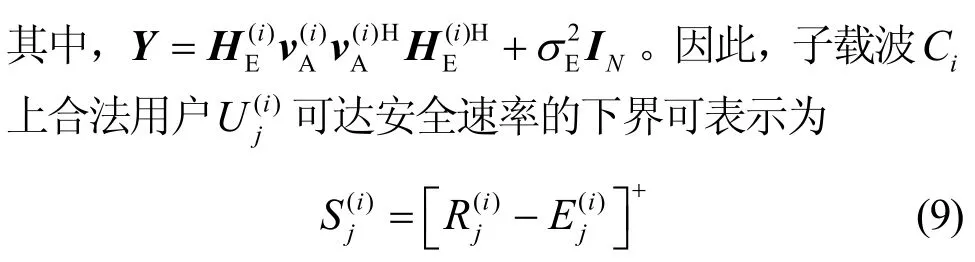
其中，[x]+表示max {x，0}。网络整体安全和速率为

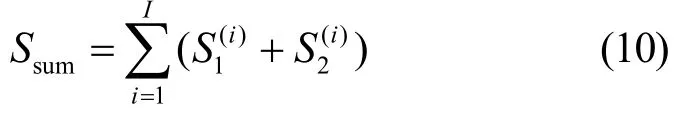
1.3 信道状态信息

本节给出的信道模型将直接应用于第2 节所建立的数学优化问题。本文假设基站能够获取所有合法链路的完美CSI。对于窃听链路，基站可以通过Eve的本振泄露进行信道估计，但由于泄露功率很小，难以获取完美CSI。因此，采用以下信道模型[23]表征窃听链路CSI 的不确定性

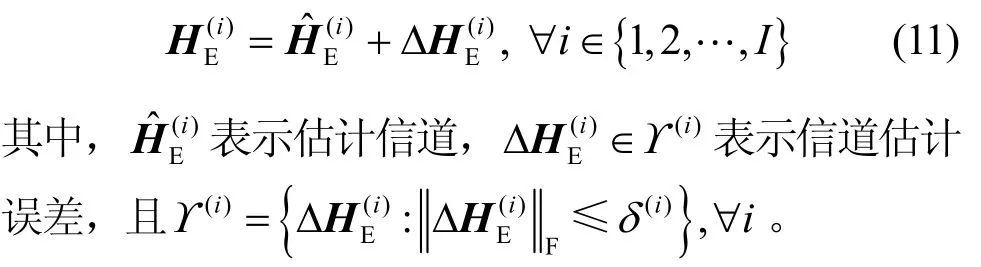
2 算法设计

2.1 AN 预编码矢量设计与问题建模

观察式(5)和式(6)，可以发现基站发射的AN 信号对合法用户的信号也造成了干扰，为提升合法用户数据速率，设计迫零AN 预编码矢量为

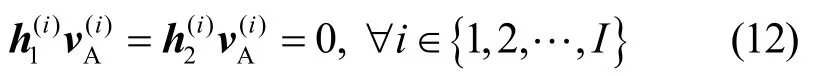
此时，子载波Ci上合法用户数据速率可重写为

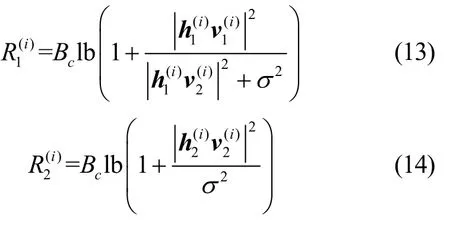
在此基础上，建立最大化安全和速率的资源分配模型为

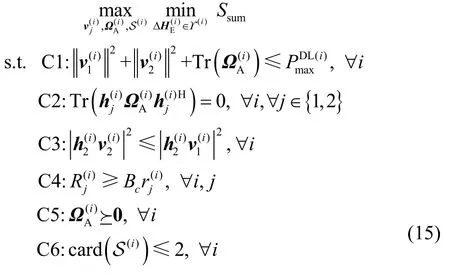
为求解问题式(15)，首先在2.2 节中假定任一子载波分配方案，提出AN 及下行数据预编码矢量优化算法；其次，在2.3 节利用匹配理论为所有合法用户分配子载波，在每轮匹配过程中，采用2.2 节提出的算法计算安全和速率作为匹配合适程度的衡量标准，通过多次迭代，最终输出一个稳定的匹配结果。

2.2 稳健性预编码矢量优化算法

假设网络中用户已分配好子载波，问题式(15)可等效为I个子问题，即

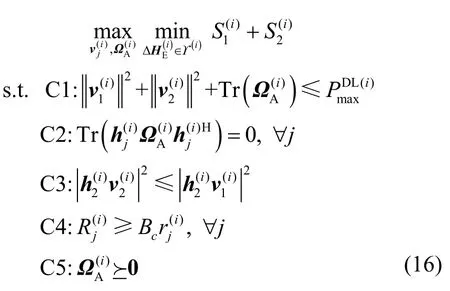
式(16)仍是一个含不确定性参数的无穷维、非凸优化问题。引入新变量，其中是一个秩为1 的对称半正定矩阵，式(16)可进一步转化为

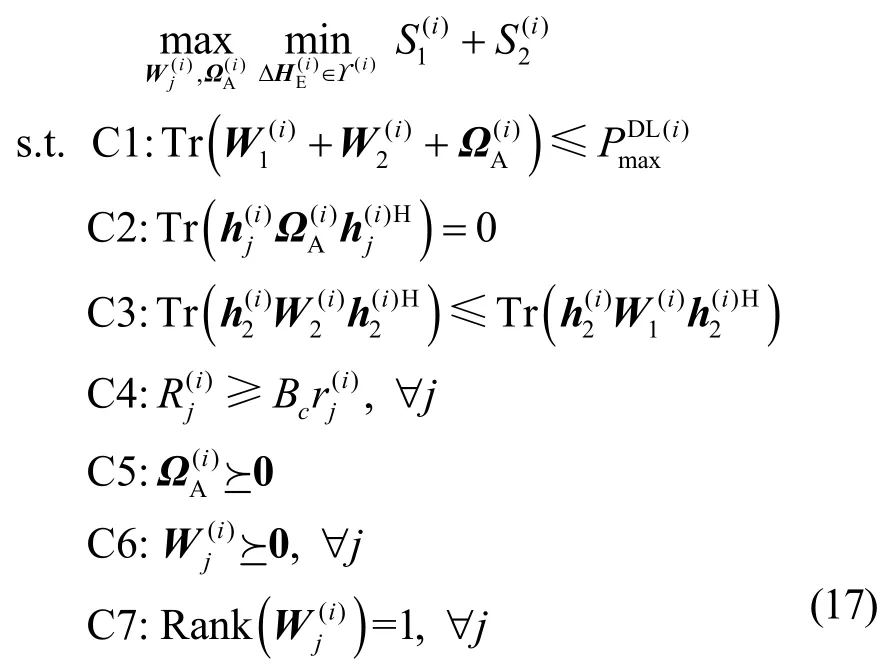
将式(17)中的目标函数转换为凸函数，根据文献[24-25]可得

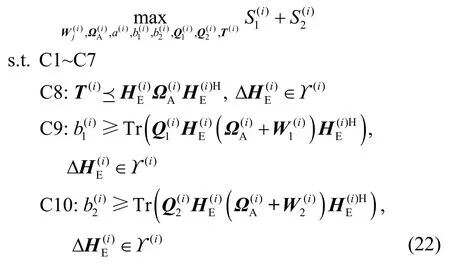
其中，目标函数表达式为

算法1稳健性预编码矢量优化算法

2.3 子载波分配算法

本文利用动态匹配理论处理子载波分配问题。定义网络中所有合法用户的集合为，考虑集合K 与I 之间进行二对一双边匹配。如果子载波Ci被分配给用户Uk，则认为Ci与Uk匹配成功。定义PF(Uk)和PF(Ci)分别为Uk与Ci的偏好表，对于子载波Ci，Ci′∈I，如果基站到Uk的信道增益在子载波Ci上较大，则认定Uk更偏好Ci，记为Uk:(Ci≻Ci′)。对于用户集合χ，χ′⊂K，满足card(χ)=card(χ′)=2，如果式(30)成立，则认定Ci更偏好χ，记为Ci:(χ≻χ′)。

其中，Ξi(χ)表示子载波Ci被分配给用户集合χ时该子载波上的可达安全速率。

定义1定义二对一双边匹配Ψ由若干个从集合K 到集合I 的映射构成，Ψ需满足以下4 个特性。

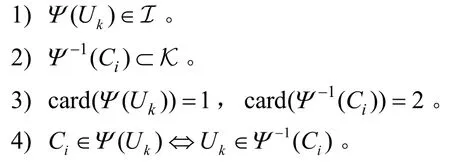
定义1中，特性1)表示每个用户可以匹配集合I中的子载波；特性2)表示每个子载波可以匹配集合K中的用户子集；特性3)限制每个用户能且只能匹配一个子载波，每个子载波能且只能匹配2 个用户；特性4)表示Ci与Uk相互匹配。为最大化系统安全和速率，可采用穷尽搜索算法寻找全局最优匹配结果，但这种方法复杂度过高。本文利用DA算法构造稳定的双边匹配，该算法的具体步骤如算法2 所示。

算法2基于匹配理论的子载波分配算法

初始化根据信道增益初始化偏好表PF(Uk)，设S(i)=∅表示分配到子载波Ci的用户集合，设表示尚未分配到子载波的用户集合

定理1算法2 必定能在集合K 与I 之间构成一个稳定匹配Ψ。

证明采用反证法证明定理1。假设Ψ不是一个稳定匹配，则存在一个子载波-用户对(Ci，Uk)，满足Ci∉Ψ(Uk)，Uk∉Ψ-1(Ci)，且Uk:(Ci≻Ci′)，Ci′∈Ψ(Uk（)即用户Uk与子载波Ci′匹配，但更偏好子载波Ci），Ci:(χ≻Ψ-1(Ci))，χ⊆Uk∪Ψ-1(Ci)，Uk∈χ（即子载波Ci与用户子集Ψ-1(Ci)匹配，但更偏好包含Uk在内的用户子集χ）。

由算法2 可知，Uk在第t次迭代中向偏好列表中优先级更高的子载波Ci发送匹配请求信息，但被拒绝。此时子载波Ci匹配用户集合χt，满足Ci:(χt≻χ)，Uk∉χt。由于算法2 迭代结束后，子载波Ci与用户集合Ψ-1(Ci)匹 配，因此Ci:(Ψ(Ci)-1≻χt≻χ)与假设矛盾。所以算法2 必定能构成稳定匹配Ψ。证毕。

2.4 计算复杂度分析

根据文献[28]，半定规划（SDP，semi-definite programming ）问题求解复杂度可表示为，其中m是不等式的个数，n是优化变量的维度，ε是求解精度。算法1中步骤1)所求解的SDP 问题不等式限制条件数量为9，优化变量维度为M，步骤2)所求解的SDP 问题不等式限制条件数量为 2，优化变量维度是N。定义X=max{M，9}，Y=max{N，2}，则步骤1)和步骤2)的计算复杂度分别为和。假设BCD 算法最大迭代次数为Nmax，又由于算法2中DA 方法的最大迭代次数为KI-2K+2，因此本文所提资源分配算法总计算复杂度为。若采用穷尽搜索算法进行子载波分配，总搜索次数为，资源分配算法总计算复杂度为，远高于本文算法。如将算法1 替换为文献[15]算法，根据文献[15]，资源分配算法总计算复杂度为，其中表示文献[15]算法的最大迭代次数。表1 总结了上述3 种算法的复杂度。

表1 算法复杂度对比

3 仿真分析

为了验证本文所提算法性能的优越性，本节利用以下6 种基准方案进行了对比研究：方案1，本文算法采用穷尽搜索子载波分配；方案2，本文算法采用随机子载波分配；方案3，OMA 传输方案；方案4，基于连续凸逼近的安全和速率最大化算法[14]；方案5，基于连续凸逼近的AN 发射功率最大化算法[15]；方案6，窃听信道信息完全已知情况下信道安全容量理论值。本文方案与方案1和方案2 对比可验证所提子载波分配算法的优越性；与方案3 对比可验证NOMA 系统相较于OMA 系统的优势；与方案4和方案5 对比可验证本文所提预编码矢量优化算法的优越性，为实现公平对比，本文将文献[14-15]中的算法扩展到多载波系统，并采用本文所提的子载波分配方案；与方案6 对比可反映出本文算法的安全和速率与理想安全和速率上限的差距。仿真中假设基站位于小区中心，用户均匀分布在半径为500 m的圆形区域内，归一化信道估计误差的上界定义为，并假设ξ(1)=ξ(2)=…=ξ(I)=ξ，为充分利用频谱资源，考虑网络中子载波被全部占用，用户数为子载波数的2 倍，并假设所有子载波上发射功率均匀分配。系统仿真参数如表2 所示。

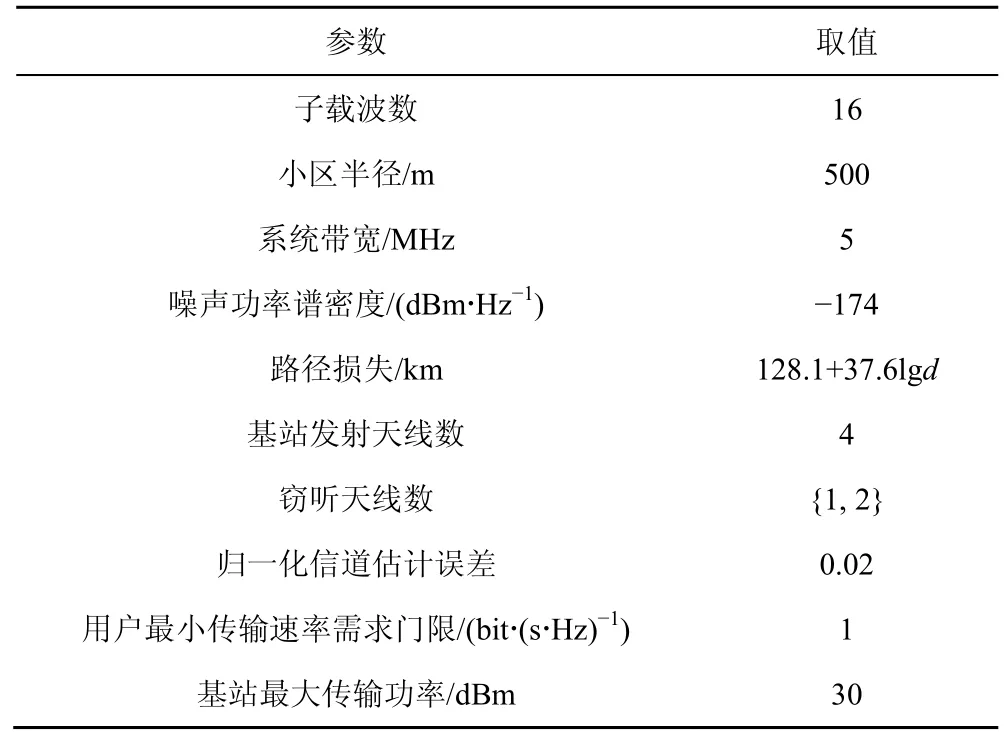
表2 系统仿真参数

BCD 算法收敛情况如图2 所示。从图2 可以看出，在不同参数取值下，算法均收敛，且迭代次数少于10 次。当窃听天线数量变少时，系统安全和速率增大，原因在于Eve 窃听能力下降，基站能够分配更多的功率进行数据传输，提升了用户数据速率。

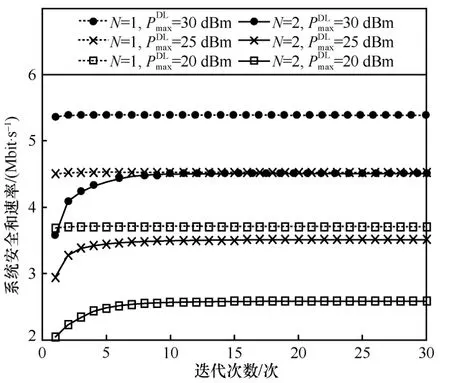
图2 BCD 算法收敛情况

图3 给出了本文算法的稳健性分析，其中归一化信道估计误差ξ取值从0.02 变化到0.30。从图3可以看出，在ξ取值范围内，系统安全和速率始终大于20 Mbit/s，说明算法具有良好的稳健性。随着ξ增大，系统安全和速率降低，这是因为信道误差越大，基站能够获取的CSI 质量越差。

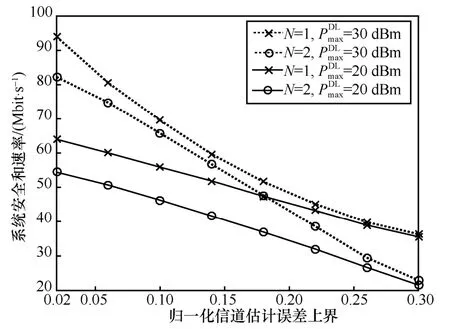
图3 本文算法的稳健性分析

不同窃听天线数目下系统安全和速率随基站最大传输功率的变化如图4 所示，其中图4(a)和图4(b)中窃听天线数分别设置为1和2。由于文献[14]算法只适用于单窃听天线场景，因此仅在图4(a)中给出。

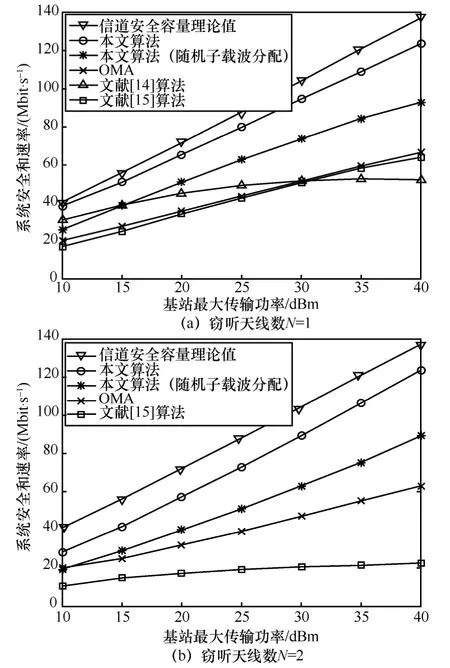
图4 不同窃听天线数目下系统安全和速率随基站最大传输功率的变化

从图4中可以看出，随着基站最大传输功率的增加，系统安全和速率随之增大。在基站功率相同的情况下，本文算法显著优于文献[14-15]算法，且安全和速率约为传统OMA 方案的2 倍。对比分析可知，本文算法性能最接近信道安全容量，且所提低复杂度子载波分配算法明显优于随机子载波分配算法。另外，文献[15]算法在窃听天线数为1 时性能增长较快，在窃听天线数为2 时性能增长缓慢，原因在于随着天线数增大Eve 窃听能力增强，文献[15]算法会分配更多的发射功率发送AN 以干扰窃听信道，分配给用户数据传输的发射功率相应减少，导致数据速率下降。

不同窃听天线数目下系统安全和速率随用户数量的变化如图5 所示，其中图5(a)和图5(b)中窃听天线数分别设置为1和2。由于文献[14]算法只适用于单窃听天线场景，因此仅在图5(a)中给出。从图5中可以看出，所有方案的安全和速率均随着用户数量的增大而增大。在用户数相同的情况下，本文方案显著优于OMA 方案和文献[14-15]方案，所提低复杂度子载波分配算法性能明显优于随机子载波分配算法。

本文子载波分配算法与穷尽搜索子载波分配算法（以下简称穷尽搜索法）的性能对比如图6 所示。由于穷尽搜索法程序在子载波数量较多的情况下运行非常耗时，因此在图6中子载波数量设置为3。从图6中可以看出，本文算法的安全和速率略低于穷尽搜索法。这是因为通过穷尽搜索能够找到使系统安全和速率最大的子载波分配方案，而所提基于匹配的算法是寻找彼此最偏好的用户与子载波组合，并不能保证达到系统最大安全和速率。当基站最大传输功率=40 dBm、窃听天线数N=1时，二者性能差距约为3 Mbit/s；当=40 dBm、N=2时，二者性能差距约为2.5 Mbit/s，相较于系统总安全和速率所占比重较小。

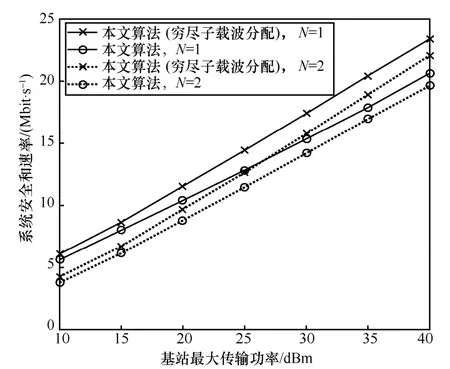
图6 本文子载波分配算法与穷尽搜索子载波分配算法的性能对比

4 结束语

本文针对下行多载波NOMA 安全传输系统稳健性资源分配算法进行了深入研究。考虑用户最小速率约束和基站最大传输功率约束，建立基于窃听信道不确定性的安全和速率最大化资源分配模型。为求解该非凸问题，将其分解为AN、数据预编码矢量优化子问题和子载波分配子问题，并对这两部分进行联合优化。基于S-procedure 算法将含不确定性参数的预编码优化子问题转化为确定性问题，利用BCD 算法求解；基于动态匹配理论将子载波分配问题重新定义为双边匹配问题，采用DA 算法求解；同时给出了算法的计算复杂度分析。仿真结果表明，本文算法具有较好的稳健性和安全性，所提子载波分配算法性能与穷尽搜索法性能非常接近，但能显著降低计算的复杂度。

本文研究工作为海量终端业务接入的5G 物联网提供了一种高频效、高安全性的信息传输手段。为更符合实际应用，后续工作将考虑同一子载波上存在2 个以上用户，非完美合法信道CSI 估计以及存在多个Eve 的场景，进一步扩展本文所提方案。

在无锡市人民医院，可视管理遍布在“自我环境管理、班组环境管理、重点设施标识、安全警示标识、物料管理标识”等多个方面，不同方面还配有不同的卡通提示标志。

附录1 秩1 解性能证明

证明优化问题式(27)的目标函数可写为

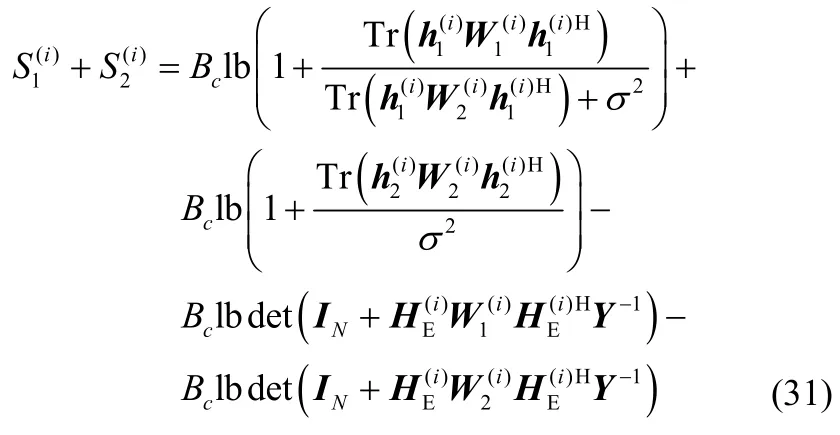
因此，只要满足式(32)～式(34)，就可以保证用秩1 解求得的目标函数不小于原解求得的目标函数。

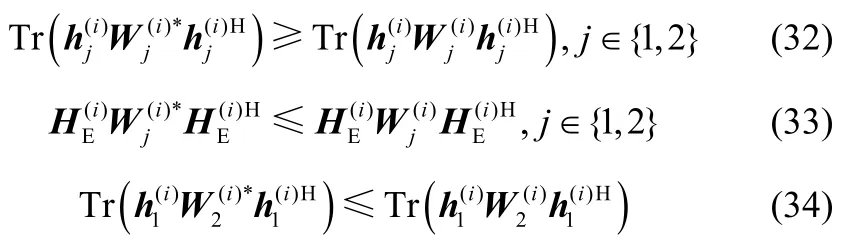
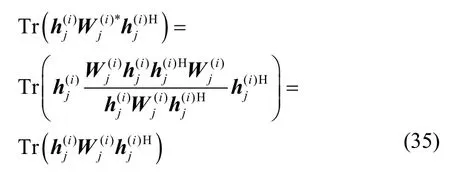
因此，式(32)成立。综上，可得出结论，通过式(28)所求得的秩1 可行解并不次于原解。证毕。