可重构的素域SM2 算法优化方法

李斌，周清雷，陈晓杰，冯峰

（1.郑州大学计算机与人工智能学院，河南 郑州 450001；2.数学工程与先进计算国家重点实验室，河南 郑州 450001）

0 引言

椭圆曲线密码（ECC，elliptic curve cryptography）算法作为公钥密码学中的一个研究重点，在性能、安全方面都被证明有很大的优势，在许多领域得到了广泛的应用。SM2 算法由国家密码管理局发布，是基于ECC 的公钥密码算法，旨在替换RSA 算法。SM2 算法作为一种国密算法，已在电子认证系统、密钥管理系统等多种商用密码产品中得到应用。

SM2 的实现依赖于椭圆曲线群上的点加、倍点和点乘的运算效率，其计算量大、结构复杂，存在算法效率不高、资源消耗较多等问题。为此，国内外众多学者对ECC 算法进行了大量的研究，包括使用FPGA（field-programmable gate array）可重部件的优化[1-3]和ASIC（application specific integrated circuit）专用芯片的设计[4-6]。但仅优化了推荐参数SM2 的计算，可扩展并行能力差，难以满足日益多样化的应用需求。同时，通过硬件实现的SM2 在运算过程中由于电磁辐射和功耗，会不可避免地泄露部分侧信道信息，容易受到能量分析攻击的威胁[7]。因此，在保证SM2 执行效率的同时提高密码系统的安全性具有十分重大的意义。

由此，本文提出了一种可重构的素域SM2 算法优化方法，通过对SM2 算法的深入剖析，结合KOA（Karatsuba-Ofman algorithm）乘法、快速模约减、Barrett 模约减、基4 求模逆、蒙哥马利点乘、点加和倍点等多种优化方法，利用FPGA 的可重构特性，实现了高能效和抗攻击的SM2 算法。同时，自顶向下设计了SM2 并行架构，可并行执行多个SM2 算法，满足各种应用场景的计算需求。

1 SM2 椭圆曲线算法

1.1 参数定义

SM2 算法包括素域和二元扩域2 种基域，对于素域，SM2 算法在素域Fp上的椭圆曲线方程为

经推导，可知

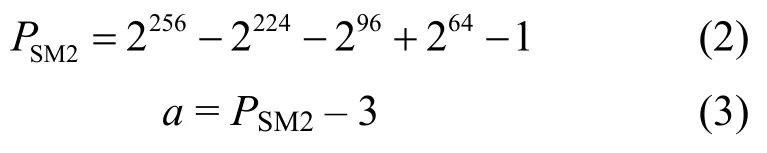
1.2 运算规则

在素域中，对于椭圆曲线上的点P、Q和无穷远点O，有以下运算规则。

1)P+O=P。

2)如果P=(x1，y1)，则-P=(x1，-y1)，且P+(-P)=O。

3)如果Q=(x2，y2)，且Q≠-P，那么P+Q=(x3，y3)，并有

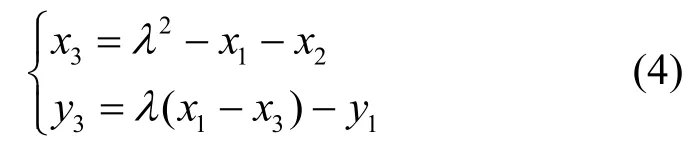
其中

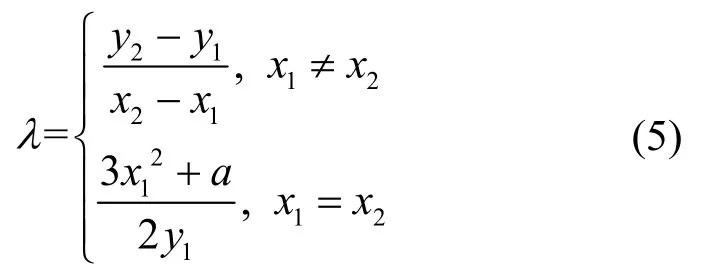
当P≠Q(x1≠x2)时，P+Q称为椭圆曲线上的点加运算；当P=O(x1=x2)时，P+Q=2P称为椭圆曲线上的倍点运算。

点乘，也称多倍点运算，是决定椭圆曲线密码体制运算速度的关键。椭圆曲线的点乘运算是指曲线上的某一基点P与一个整数k进行乘法运算，也就是k个P相加，即

由以上分析可以看出，对点加、倍点和点乘的优化是提高SM2 计算效率的重要手段。

1.3 算法分析

从SM2 的定义和运算描述中可以看出，它以大数模运算为基本运算，运算量大、耗时长，模运算的效率直接决定了SM2 的计算速度。其次，不同坐标系下椭圆曲线的计算式也会发生变化，坐标系的选择和计算式的优化对SM2 的计算速度也有很大的影响。最后，如何利用FPGA实现高效的、可扩展的和适用的SM2 也面临严峻的挑战。

为此，国内外学者对椭圆曲线的优化加速展开了广泛的研究。文献[8]设计了4 个模乘模块，可并行计算点乘的运算。文献[9]在Jacobian 坐标系下，利用交叉模乘，减少了资源占用和时延。文献[10]在FPGA 上优化实现了FourQ 椭圆曲线，并设计了单核和多核结构。文献[11]提出了快速模逆算法，采用基为8 的扩展欧几里得算法减少了计算周期。文献[12]结合Karatsuba、快速模约减和蒙哥马利点乘实现了美国国家标准与技术研究院（NIST，National Institute of Standards and Technology）素域的ECC 算法。文献[13]采用基为4 的交叉模乘和最大公约数求模除优化了SM2 素域和二元扩域算法。文献[14]设计了多种素域乘法运算，包括Booth 乘法、Moore 乘法等，并结合快速模约减实现了模乘运算。文献[15]使用Toom-Cook算法减少了椭圆曲线中模乘的运算量。文献[16]结合多种算法和优化技术实现了支持一般参数的蒙哥马利和Weierstrass 椭圆曲线算法。文献[17]在雅可比坐标系下，使用基为2 的交叉模乘及蒙哥马利点乘优化了素域ECC 算法。但是，SM2 的计算复杂度和具体的实现结构、坐标系、点乘算法、模乘算法、模逆算法等紧密相关，一部分方案仅优化了模乘和模逆算法；另一部分方案仍采用基为2 的低基数实现方式；其他方案未涉及多模块并行的架构设计。另外，大多数方案仅考虑了推荐参数（国家密码管理局和NIST 推荐的椭圆曲线参数）的椭圆曲线，并未涉及任意参数的实现。同时，大多数方案并未在FPGA 上实现坐标系的转换。

由以上分析可以看出，要提高SM2 的FPGA 实现速度，一是要对关键路径进行分解，深度优化，提高计算效率；二是要增加并行度，包括各模块间的并行和同时处理数据的能力。为此，需要从SM2 的各个计算阶段着手分析，结合FPGA 可重构的特性，针对不同的运算、存储和通信特征选择合适的实现方式。本文选择标准射影坐标系，采用蒙哥马利算法实现点乘，并利用KOA 乘法、快速模约减、模加减实现点加和倍点运算，以极大提高SM2 算法速度。其中，KOA 乘法采用DSP 实现，快速模约减、模加减采用加法器和查找表实现。然后，实例化多个点加和倍点模块，两两一组形成点乘运算，从而实现SM2的多路并行计算。最后，利用Barrett 算法实现任意参数的快速模乘运算，并使用基为4 的扩展欧几里得算法实现模逆，完成坐标系的转换。

2 SM2 的优化设计

2.1 SM2 整体架构

SM2算法整体架构如图1所示。该架构采用CPU+FPGA 的方式实现，并通过PCIe 进行数据的传输。其中，CPU 主要完成信息的配置、中间状态的查询和最终结果的显示；FPGA 主要完成SM2 的加速计算，其核心模块包括点乘、点加、倍点和坐标转换。通过CPU 重构FPGA 完成电路逻辑配置，再以软硬件协同方式实现SM2 的加密、解密、签名、验签和密钥交换等功能。

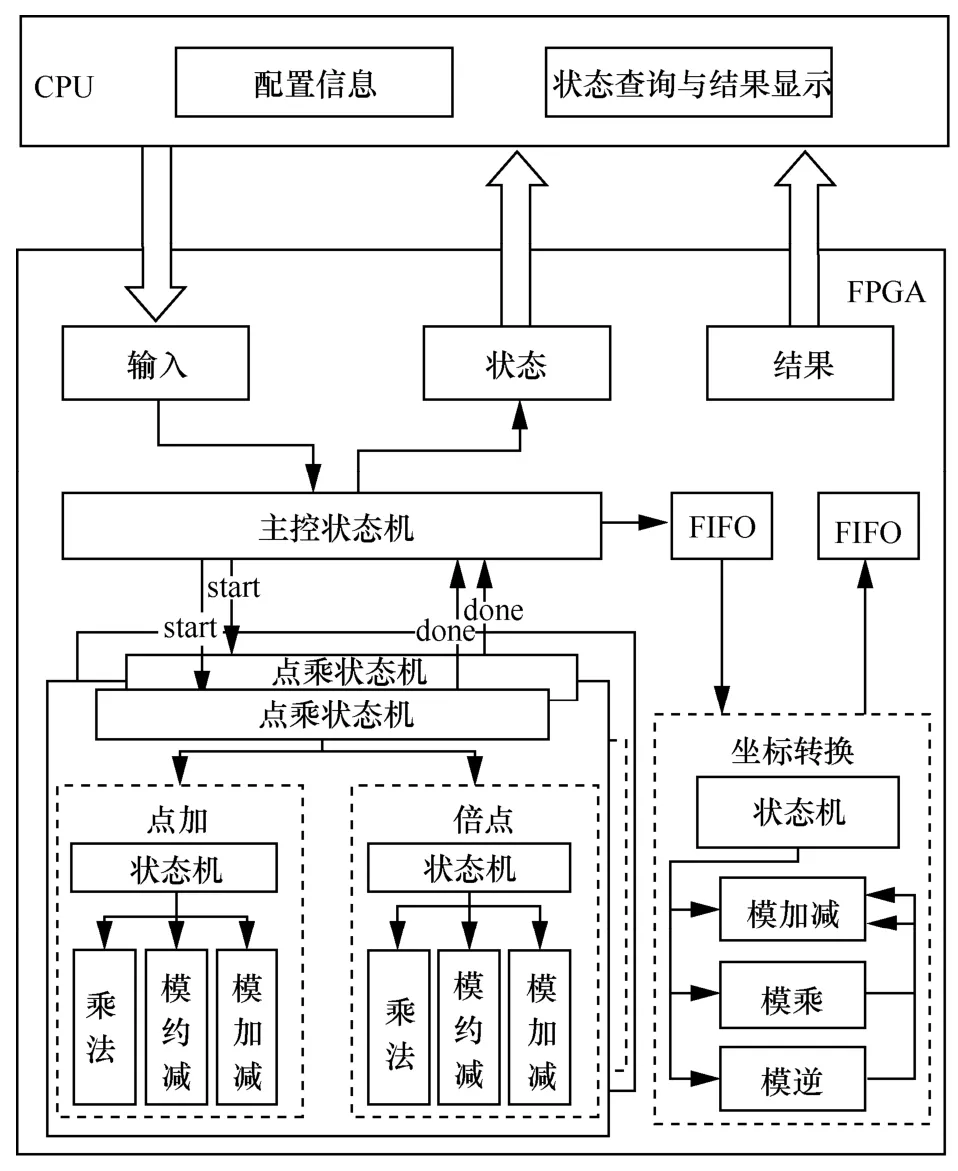
图1 SM2 算法整体架构

在计算SM2 点乘时，会多次调用点加和倍点运算，而坐标转换只在最后计算一次，因此本文对点加和倍点以性能最优进行优化，而对坐标转换以资源最优进行优化。其次，由主控状态机对多个点乘模块进行调度管理，实现SM2 的并行处理，满足不同应用场合的计算需求。最后，各点乘模块共享模加减模块，实现资源的复用，并通过异步FIFO 完成数据的传输，以减少FPGA 资源的消耗。

由此可见，本文通过优化底层各种模运算，再以并行和资源共享的方式实现多路点乘，完成了SM2 的FPGA 可重构优化设计，支持多种参数的动态配置。此外，本文以CPU和FPGA 搭建了异构架构，通过并行调度和协同计算，并以重构FPGA提供高并发和多任务处理阵列，保证了高效能密码运算的业务需求。

2.2 快速模乘

快速模乘采用KOA 乘法和快速模约减实现，先由KOA 算法完成2 个大数的相乘，再由快速模约减算法完成结果的取模运算。其中，KOA 算法和快速模约减算法计算周期分别为一个时钟，则快速模乘可在2 个时钟内完成整个运算。

2.2.1 KOA 快速乘法

KOA[18]算法的核心思想是“分而治之”，采用递归的方式将一个复杂的乘法运算分解成多个简单的乘法运算，较传统计算速度更快、效率更高。对于2 个n位数，如果直接相乘，其复杂度为O(n2)；如果使用KOA 算法，可以将复杂度降低到O(nlb3)。

其中，C2=AH×BH，C1=AH×BL+AL×BH，C0=AL×BL。而C1又可表示为C1=(AH+AL)×(BH+BL)-C2-C0，由此，整个算法只需要计算乘法AH×BH、AL×BL和(AH+AL)×(BH+BL)，从而降低了复杂度。

对于SM2，其参数为256 位，而FPGA DSP 支持最大位宽为64 位的乘法运算，那么可以将256 位分割成128 位，再将128 位分割成64 位，经过两次递归运算，得到最终的结果。另外，C2×2n和可直接通过向左移位（＜＜）完成，如算法1 所示。

算法1KOA 乘法

输入A，B，n//n为位宽

输出C

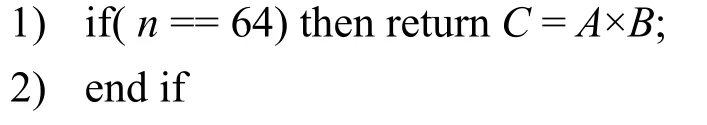
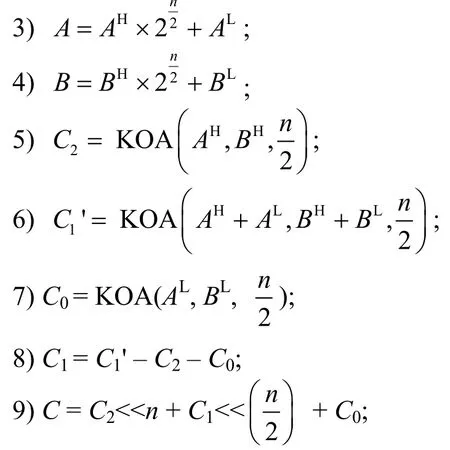
为进一步优化KOA 算法在FPGA 上的实现，本文将64 位DSP 乘法时钟周期设置为0，并通过wire 类型变量将各个模块互连。当256 位数据输入时，可立即计算出结果，并由寄存器缓存输出，整个计算过程为一个时钟。128 位KOA 乘法的FPGA硬件结构如图2 所示。

图2128 位KOA 乘法的FPGA 硬件结构

对于256 位KOA 乘法，与图2 结构相同，只需将DSP 64 位乘法替换为128 位KOA 乘法即可。这样，通过第一层调用256 位KOA 算法，第二层计算128 位KOA 乘法，第三层调用DSP 并计算64位乘法，逐层完成计算。

2.2.2 快速模约减

对于素数域SM2 算法，当PSM2给定时，可以通过多次模约减操作替代除法操作，从而快速求得取模的结果，称为快速模约减[19]。

设c=a×b且0≤a＜PSM2，0≤b＜PSM2，则0≤c≤，于是c可以表示为

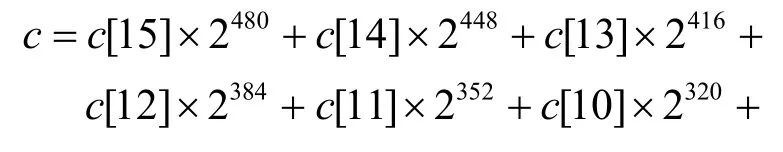
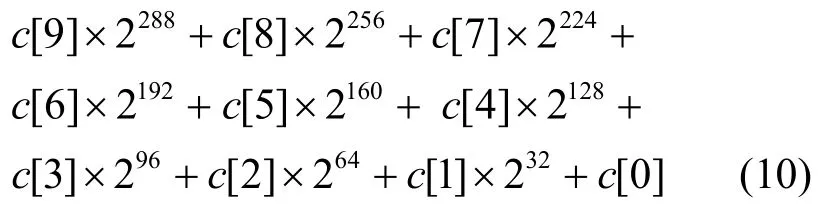
其中，c[i]∈[0，232)，0≤i≤15。

定义256 位数组s为

则sum=(s[0]+s[1]+s[2]+s[3])×2+s[4]+s[5]+s[6] +s[7]+s[8]+s[9] -s[10] -s[11] -s[12] -s[13]，那么cmodPSM2=sum modPSM2，显然快速模约减将模除运算变为模加减运算，从而大大降低了算法的复杂度。

进一步，对数组s的运算进行观察分析可以看出，c[8]+c[9]+c[10]+c[11]被执行了3 次，c[12] +c[13]+c[14]+c[15]被执行了6 次。因此，可以对频次高的组合数值进行预计算，以此简化后续计算步骤。这里，令r0=c[15]+c[14]，r1=r0+c[13]，r2=r1+c[12]，r3=(c[11]+c[10]+c[9])+c[8]，r4=c[13]+c[8]，r5=c[14]+c[9]，r6=r2+r3，则sum的计算可由117 个8 位加法器在一个时钟内完成。而未优化时，则需要13×32=416 个加法器。

同时，sum 最大不超过14PSM2，可以通过预计算提前给出kPSM2(0≤k≤15)的值，然后根据sum 的高4 位选择对应的kPSM2，并使用2 次减法完成模约减。然而，在减法过程中可能产生溢出，这里以carry1和carry2为溢出标志位，并根据carry1是否产生溢出而选择result1或result2作为结果，具体如算法2 所示。

算法2快速模约减优化

输入sum[259:0]，PSM2，kPSM2

输出c_reduce

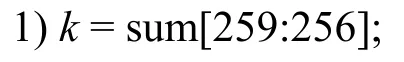
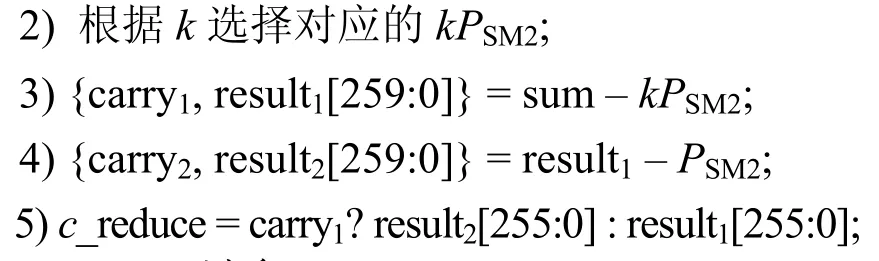
2.2.3 Barrett 模乘

Barrett 算法[20]利用乘法和模约减运算代替了高成本的除法来实现取模运算，可计算任何参数的模乘。对于0≤a＜PSM2，0≤b＜PSM2，则a×b＜。为计算c=a×bmodPSM2，0≤c＜PSM2，令d=a×b，如果存在e使d=e×PSM2+c，则可求得c。

其中，n。对于e′的计算，由除法转变为了乘法，且和可以通过向右移位（＞＞）的方式实现，大大降低了计算量。而对于μ的计算，可以使用软件提前计算出来，例如当模数PSM2为FFFFFFFE FFFFFFFF FFFFFFFF FFFFFFFF 7203DF6B 21C6052B 53BBF409 39D54123 时，对应的μ值为1 00000001 00000001 00000001 000000018DFC2096FA323C0112AC6361 F15149A0。在大部分应用中，一旦选定模数PSM2，其在计算过程中就保持不变，因此μ只需要计算一次即可。最后，对于结果c，其取值范围为[0，2PSM2)，因此对c与PSM2进行比较判断，并计算输出最终结果。Barrett 模约减整体流程如算法3 所示。

算法3Barrett 模约减算法

输入a，b，PSM2，

输出c=a×bmodPSM2

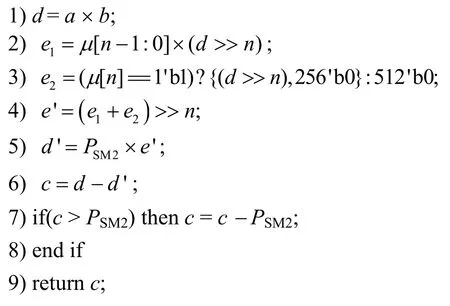
在算法3中，μ可能为257 位，因此最高位μ[n]也要参与计算，步骤2)～步骤4)为e′的乘法及向下取整操作。显然对于Barrett 模约减，必须借助高效的大数乘法才能发挥其优势。因此，算法3中的步骤1)、步骤2)和步骤5)均采用KOA 乘法快速实现，对应的硬件结构如图3 所示。

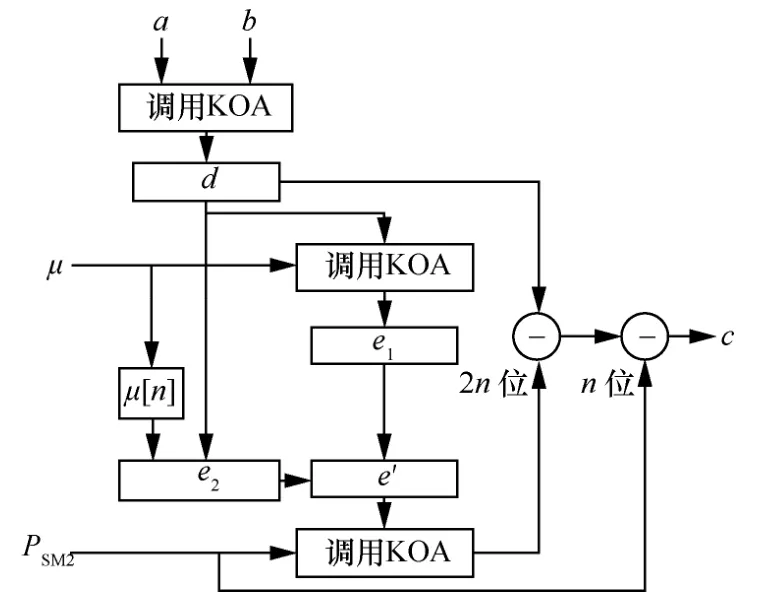
图3 Barrett 模约减结构

从图3中可以看出，Barrett 模约减计算周期为T=3TKOA+2TSUB+TADD，且关键路径为KOA 算法。

2.3 扩展欧几里得求模逆

对于素数a∈[1，PSM2-1]，如果存在a-1，使a×a-1≡1modPSM2，则a-1称为a的模逆元。通常在素数域上求模逆的算法有扩展欧几里得、费马小定理和蒙哥马利算法。虽然，扩展欧几里得算法采用辗转相除法，但可以根据公约数的性质，将除法全部改成加减运算，并以二进制移位完成除2 运算，有利于硬件实现。而费马小定理需要求a的次幂，蒙哥马利算法与扩展欧几里得算法原理较相似，但需要将结果从蒙哥马利域转到实数域，计算效率较低。

2.3.1 基4 的模逆优化

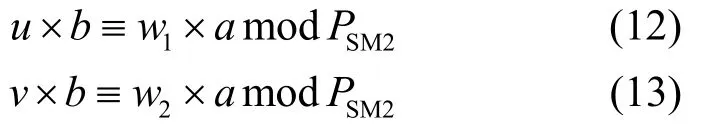
其中，u、v、w1、w2分别初始化为a、PSM2、b、0。然后用扩展欧几里得算法对u和v进行计算，同时对w1和w2进行相应的线性变换，确保式(12)和式(13)保持成立。最后，当v=0 时停止迭代，此时有u=1，w1即所求的结果。

另外，以四进制表示，采用状态机循环控制，对该算法进行优化。在每次迭代中，根据u和v的最后两位对其进行判断计算。当最后两位为2′b00或2′b10，即u和v为偶数时，进行除以4 或2 的操作。当最后两位相同时，将u和v相减，并进行除以4 的操作；否则，将u和v相减，并进行除以2的操作。具体流程如算法4 所示。

算法4扩展欧几里得模逆算法

输入a，b，PSM2

输出c=modPSM2

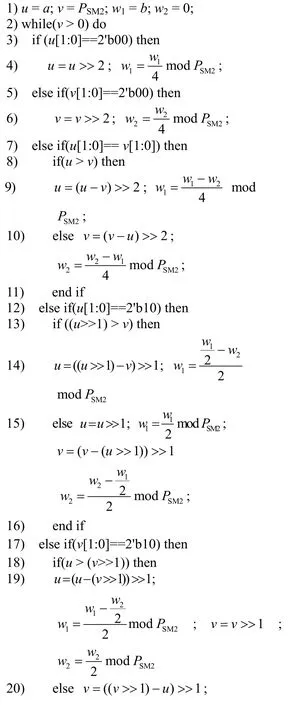
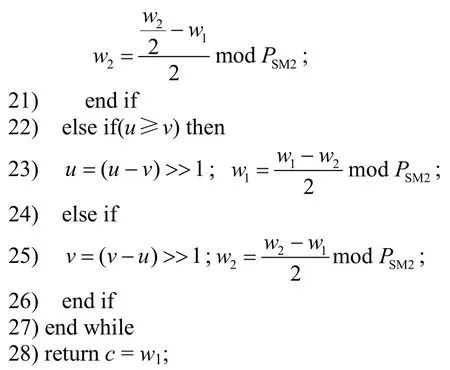
在算法4中，步骤1)为初始化状态；步骤2)为循环判断状态；步骤3)～步骤26)分别为各种判断和计算；步骤28)为输出。其次，对于u和v的计算始终保证其结果值小于PSM2，不需要额外处理。而w1和w2这2 个数的加减可能大于PSM2或者溢出，且除以2和4 需要额外进行判断并调用模加减来处理。具体的计算式为

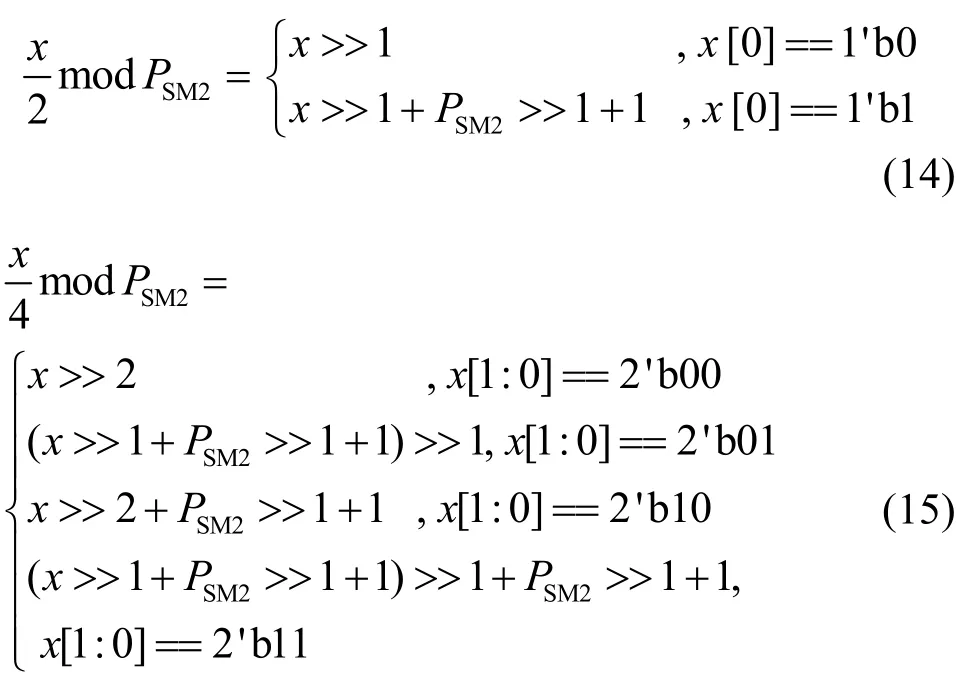
2.3.2 模加减优化

为求模逆元，需要用到模加减操作，这里将其合并在一个模块中实现，以减少资源占用。该模块根据模加减模式选择不同的初值进行计算，其中模加的结果可能超过PSM2，因此结果需要再减去PSM2；而模减的结果可能为负数，因此可先加PSM2再做减法，并根据溢出标志位判断最终的输出结果，如算法5 所示。

算法5模加减

输入a，b，PSM2，SEL

输出c=a±bmodPSM2

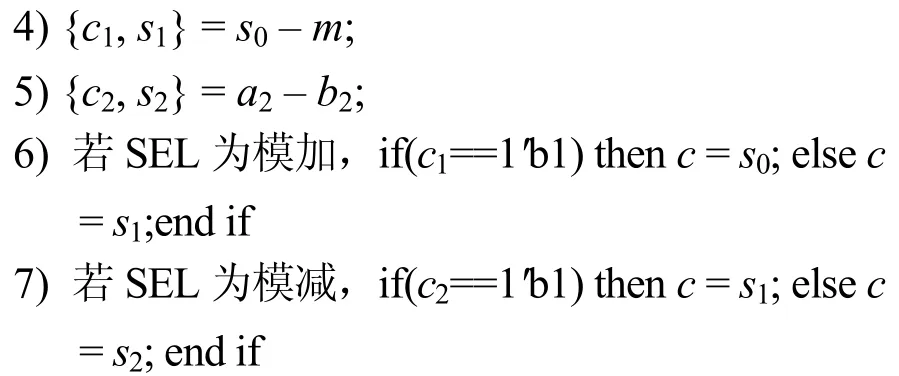
算法5中，SEL 为模式选择，根据模加和模减对a1、b1、a2、b2和m赋不同的初值，并通过步骤3)～步骤5)完成计算，其中c0、c1、c2为溢出标志位，可根据c1、c2的值确定最终的计算结果。

2.4 点乘优化

2.4.1 蒙哥马利点乘

点乘算法有二进制展开扫描法、NAF（none adjacent form）扫描法、NAF 滑动窗口法及蒙哥马利点乘算法[21]。目前，蒙哥马利点乘算法是实现效率最高和应用范围最广的算法。蒙哥马利点乘算法首先根据基点G，计算初始值R0和R1，R0=G，R1=2G；然后根据整数k的二进制编码的每一位对R0和R1进行点加和倍点运算；最后根据k的二进制位数进行循环计算，并求得最终点乘结果。其具体运算过程如算法6 所示。

算法6蒙哥马利点乘

输入k=(kl-1，…，k0)，点G

输出Q=kG

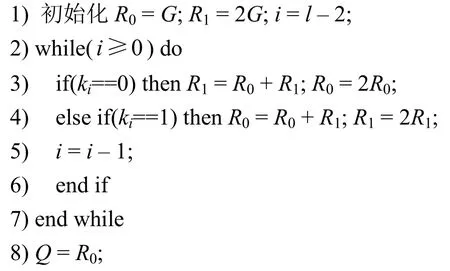
从算法6中可以看出，无论ki的取值如何，每一次的循环过程中都会计算点加和倍点，且两者相互独立，可并行执行。同时，由于点加和倍点同时计算，使点乘运算过程中泄露的功耗信息无律可循，可有效抵抗简单功耗攻击（SPA，simple power analysis）。

2.4.2 点加和倍点优化

Fp上的椭圆曲线常用的坐标系有仿射坐标系、标准射影坐标系、Jacobian 加重射影坐标系和LD（Lopez &Dahab）射影坐标系。不同的坐标系表示在计算点加和倍点时的运算效率不同。这里，选择标准射影坐标系完成计算，并在最后一步进行坐标系转换。同时，为提高点加和倍点的计算效率，蒙哥马利点乘只需x坐标参与计算，并在最后一步计算y坐标，大大简化了计算过程。

在标准射影坐标系下，有点P(X1，Y1，Z1)和点Q(X2，Y2，Z2)，则点加和倍点的计算式[22-23]分别为

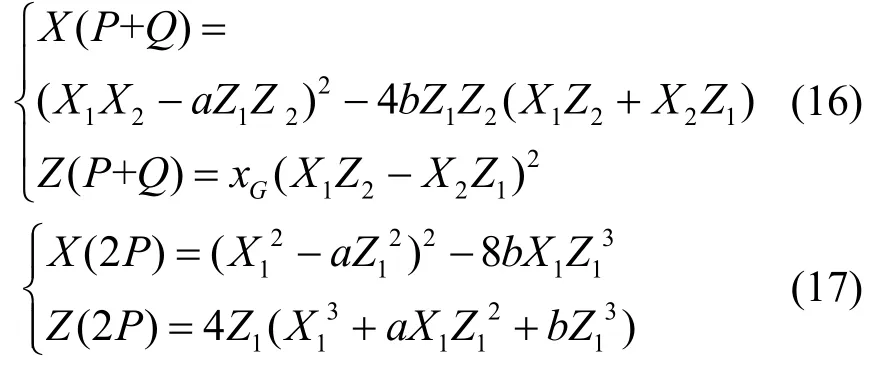
最后，将结果转换为仿射坐标系，有

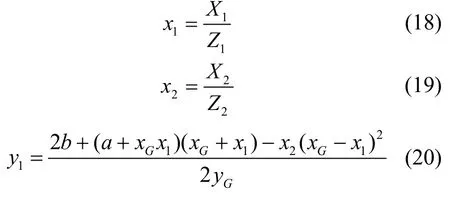
则点(x1，y1)即所求，其中(xG，yG)为基点G的坐标。

通过对比可以看出，在仿射坐标系下，每次计算点加和倍点时都需要求模逆。而模逆计算周期长，计算复杂度高，难于优化。如果采用标准射影坐标，就可以消除点乘迭代过程中的模逆运算，从而提高运算效率。同时，在标准射影坐标下，会将投影点和仿射点进行一一映射，运算开始时将仿射坐标变换到射影坐标中表示，运算结束时再映射回仿射坐标。所以在整个运算过程中，仅在最后一次使用模逆运算，中间迭代过程没有模逆参与。

2.4.3 数据流优化

为进一步优化点加和倍点的计算效率，本文对数据流进行了深度优化，使其在最短的时间内完成计算。由于快速模乘由KOA 乘法和快速模约减2个模块组成，且都可在一个时钟内计算出结果，因此本文调整点加和倍点的部分计算流程，交替调用KOA 乘法和快速模约减模块，充分发挥计算效率。

点加和倍点计算过程和数据流分别如表1和表2所示。

从表1和表2中可以看出，经过12 个时钟，即可完成点加和倍点的计算。

表1 点加计算过程和数据流

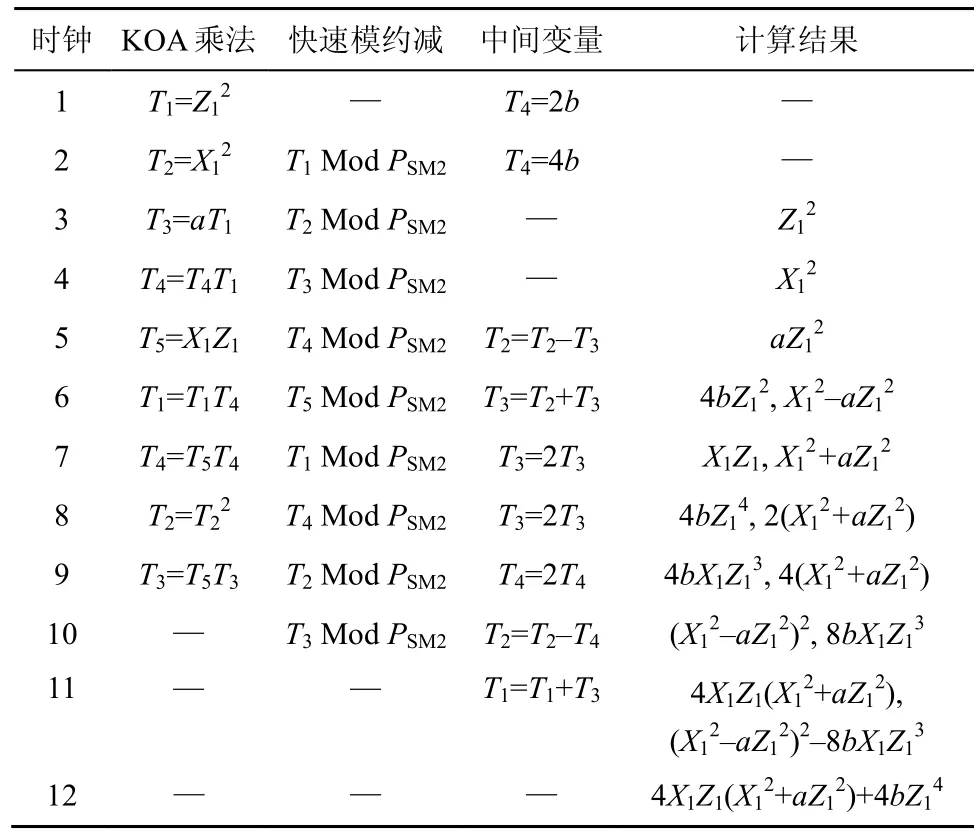
表2 倍点计算过程和数据流

2.5 并行调度管理

为了进一步加速SM2 的计算，在FPGA 上实例化多个模块，各模块相互独立，由上层状态机调度管理，从而实现多任务的并行处理，提高可扩展性。这里采用贪心策略对任务进行分发，当计算完成时，进行仲裁汇总，并以地址为标识将对应的结果上报给CPU。假设SM2 并行模块数为n，具体流程如下。

1)任务分发

①从0 到n轮询SM2 是否空闲，如果存在空闲模块i，跳转②；否则继续执行①。

②根据i对应的地址，将任务和控制命令载入第i个SM2 模块对应的RAM。

2)执行计算

①第i个模块从RAM中读取自身的任务和控制命令。

②如果控制命令为开始，则说明任务已配置好，开始计算；否则跳转①继续等待。

3)结果汇总

①当第i个模块计算完成时，将地址、完成标志位和结果写入第i个FIFO。

②从0 到n轮询所有FIFO，如果完成标志位为1，将该结果汇总到最终的一个FIFO，并上报。

其中，步骤1)～步骤3)并行执行，并通过异步RAM 或FIFO 进行数据传输。任务分发可依次写入多个任务，各SM2 模块收到任务后，开始并行计算。最后将结果汇总到一个FIFO中，并由CPU 依次读取结果。

3 实验结果与分析

本文实验的硬件平台是由4 块大规模FPGA 构成的加速卡，芯片型号为Xcku-060-ffva1156-2-i，软件为Vivado 2019.2。

3.1 各模块实现

在FPGA 上以8 路并行实现SM2 整体算法，其各模块时钟频率、资源占用和计算周期的具体情况如表3 所示。

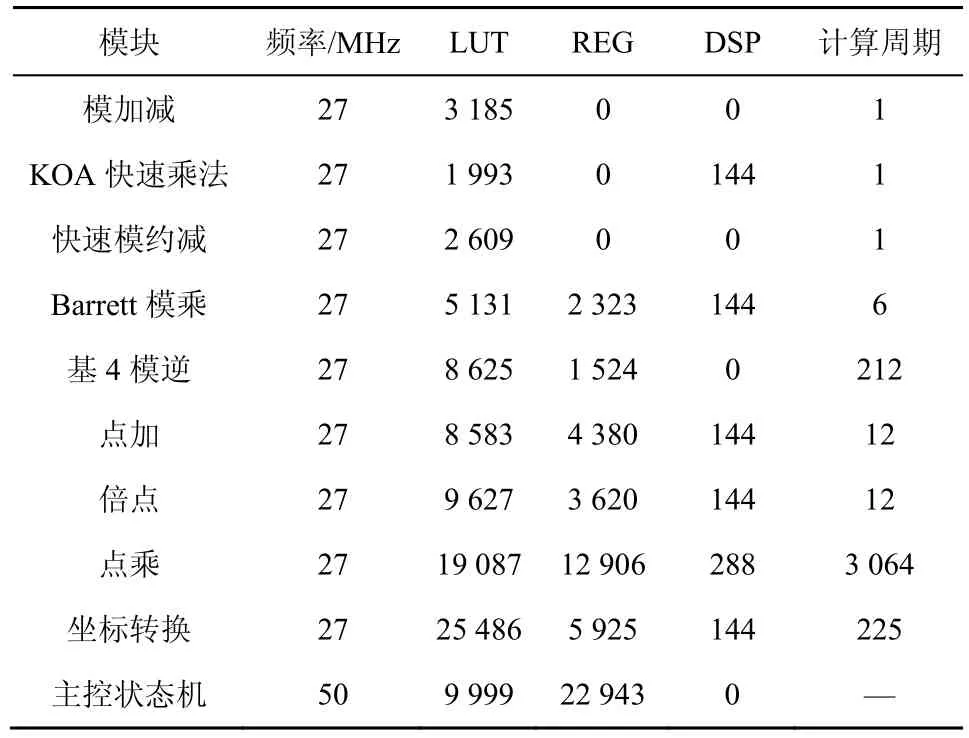
表3 SM2 各模块实现情况

从表3中可以看出，单个SM2中各模块占用资源适中，充分利用了LUT、REG和DSP 等资源。其中，点乘频率为27 MHz，经过3 064 个时钟即可完成计算。当8 路SM2 并行时，整体占用FPGA 总LUT 资源的比例为60.23%，REG 为24.48%，DSP 为88.70%，整体功耗仅为3.375 W。由于FPGA 总的DSP 个数为2 760，当前实现共占用2 448 个，其使用接近饱和，具有较高的资源利用率。显然，如果拥有更多的DSP资源，SM2 的性会进一步提高。

3.2 性能分析对比

表4 给出了不同坐标系下点加和倍点运算次数对比。其中，I、M和S 分别表示模逆、模乘和模平方运算。显然，蒙哥马利方法优于其他方法，对于点加，其经过8 次模乘、2 次模平方即可完成计算；对于倍点，其经过6 次模乘、3 次模平方即可完成计算。

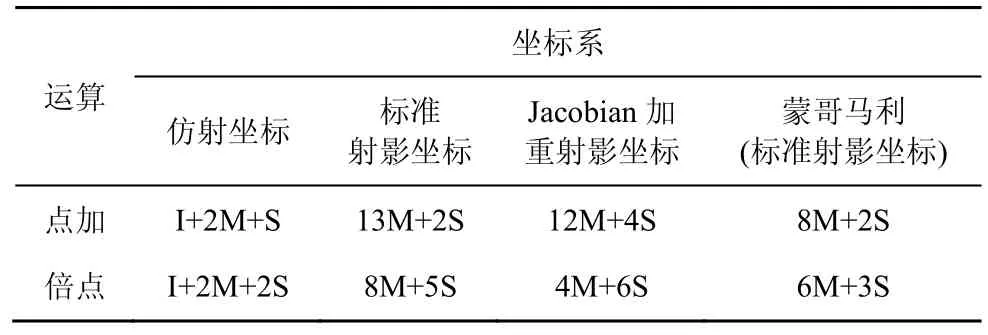
表4 不同坐标系下点加和倍点运算次数对比

对于点乘，在计算k倍点时，设k的比特数为l，如果采用二进制展开法，需要l次倍点和次点加运算；NAF 扫描法需要l次倍点和次点加运算；NAF滑动窗口法需要约l次倍点和次点加运算，其中ω为窗口宽度；蒙哥马利法需要l次倍点和l次点加运算。但是对于FPGA，蒙哥马利倍点和点加可并行计算，相当于整体只需要l次运算，而其他方法无法并行且整体运算次数明显大于l。显然，蒙哥马利法具有更好的计算性能。

其次，表5 给出了FPGA 与CPU SM2 的速度对比。其中，FPGA 的速度为4 块FPGA 的速度总和。

表5 FPGA 与CPU SM2 的速度对比

最后，将本文方案与其他硬件方案的点乘进行性能对比，如表6 所示。

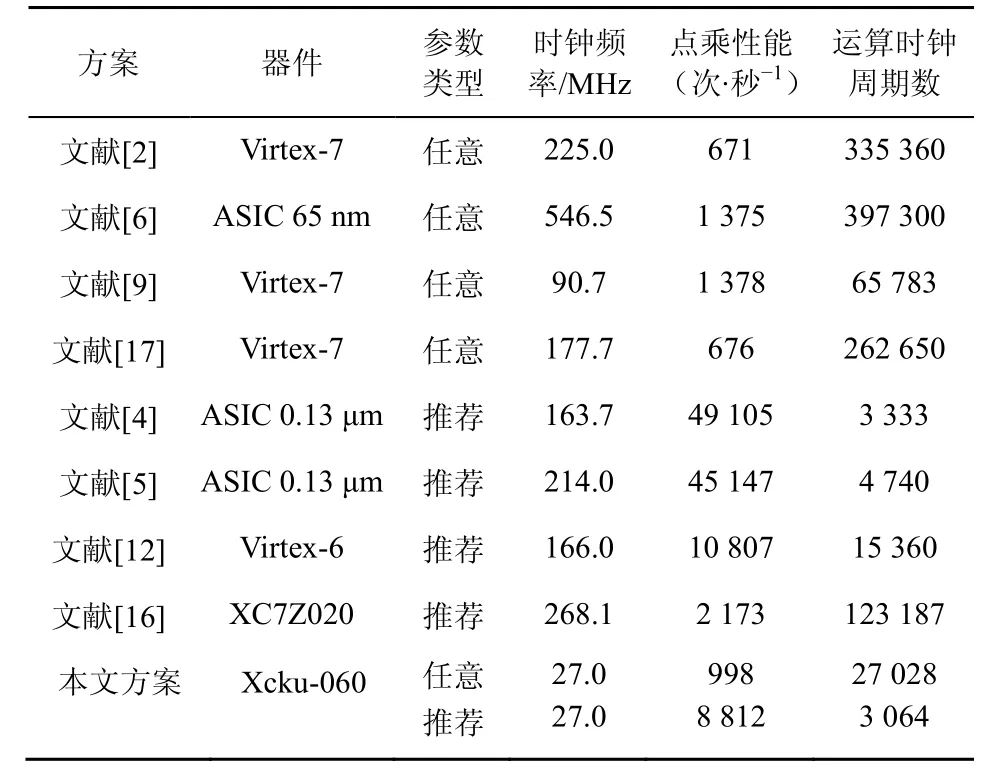
表6 本文方案与其他硬件方案点乘性能对比

从表6可以看出，无论是任意参数还是推荐参数，相比于其他FPGA 实现，本文方案的点乘周期要远低于其他方案。在点乘性能方面，由于时钟频率较低，单个模块的计算性能不如其他部分方案。但是本文方案在FPGA中实例化了8 个模块，对于任意参数，其总速度为7 984 次/秒，高于其他方案；对于推荐参数，其总速度为70 496 次/秒，远高于文献[4-5]的ASIC实现，且当加速卡4 块FPGA 同时工作时，其最高总速度更是达到了281 984次/秒，具有十分可观的效率。

3.3 安全性与资源对比

SM2 算法除了对运算速度的要求外，还必须具备一定的抗攻击能力。而SPA 是最常见的攻击方式。本文SM2 算法每次都执行点加和倍点，且点加和倍点的功耗波形不存在差别，攻击者无法得到运算规律，可有效抵抗SPA。

此外，面积与时间的乘积AT 客观反映了资源消耗和算法性能之间的关系。AT 值越低，表明在有限的资源条件下，与性能之间取得的平衡越好。这里，将本文方案与其他FPGA 实现方案在安全性和AT 值方面进行了对比，如表7 所示。

从表7中可以看出，本文SM2 算法在具有抗SPA 的同时，也具有较优的AT 值。对于任意参数的椭圆曲线密码算法实现，虽然文献[2]占用资源少，AT 值低，但它不具有抗攻击性。此外，由于文献[2]采用蒙哥马利模乘，需要额外进行预处理并对结果进行转换。

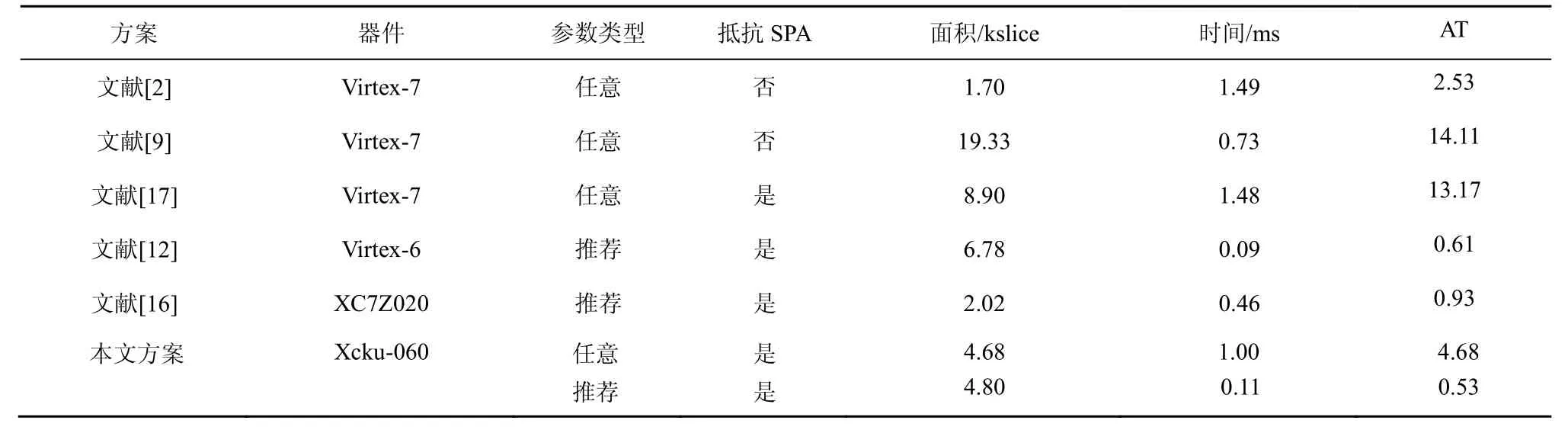
表7 本文方案与其他FPGA 方案在安全性和AT 值方面的对比

最后，将本文方案与其他FPGA 实现的SM2算法进行了综合对比，包括抗攻击性、性能和AT值等方面，结果如表8 所示。

从表8中可以看出，本文方案在性能和AT 值方面均高于其他方案，性能至少提高了3.26 倍，AT值至少提高了4.84 倍，且具有抗攻击性。这是由于本文方案深度优化了模乘运算，并优化了点加和倍点计算流程，缩短了点乘周期，提高了计算性能。同时，本文合理利用了FPGA 逻辑资源，减少了资源消耗，具有较优的AT 值。

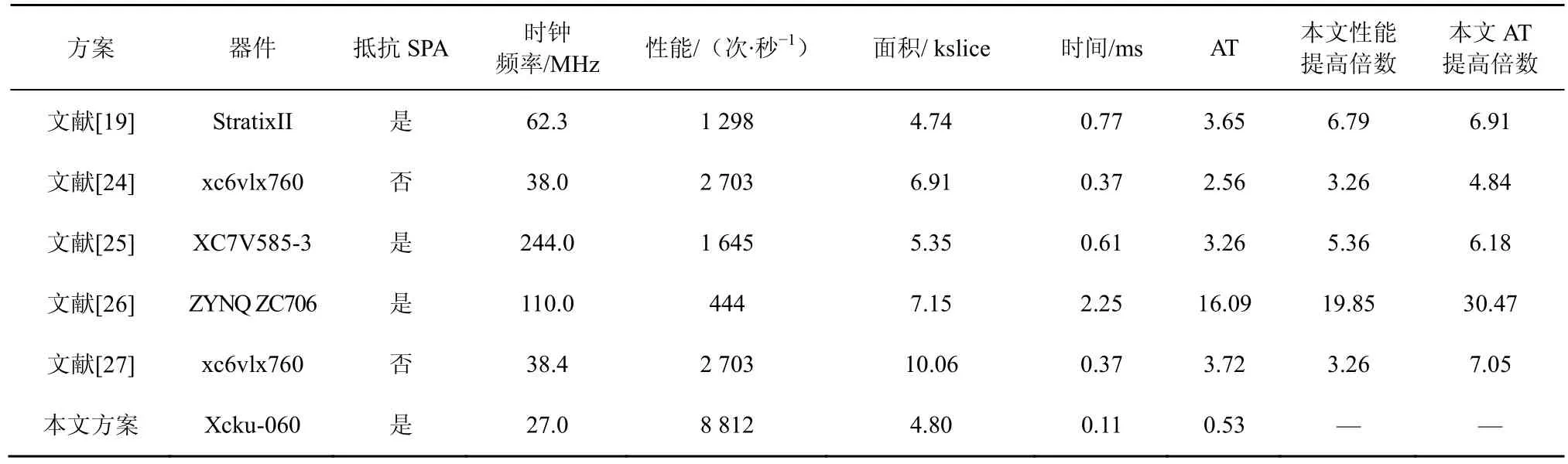
表8 本文方案与其他FPGA 实现的SM2 算法综合对比

3.4 应用与可扩展性分析

SM2 签名/验签、加解密和密钥交换过程中会多次调用点乘。以签名/验签应用为例，在签名过程中会调用一次点乘和多次SM3 哈希值计算，在验签过程中会调用两次点乘和多次SM3。为节省资源，对于SM3 采用将两轮压缩为一轮的串行方式实现；中间大数的模乘、模逆及坐标转换采用共享模块的方式实现，具体资源占用如表9 所示。

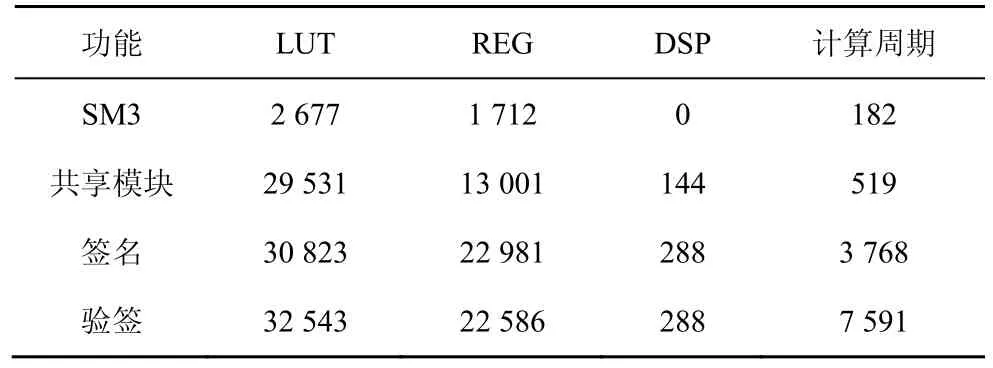
表9 SM2 签名/验签的具体资源占用

在27 MHz 频率下，由表9中的计算周期计算可得，单模块签名速度为7 165 次/秒，验签速度为3 556 次/秒。文献[28]签名速度为26 063 次/秒，但其未提及SM3 算法和坐标系转换的耗时。本文方案FPGA 可用8 个模块并行执行，当以一个SM3模块+8 个点乘模块+一个共享模块的架构实现时，总签名速度即点乘速度为70 496 次/秒，具有更高的计算效率。

在可扩展性方面，本文SM2 的并行架构在工程实现上方便移植。根据不同FPGA 芯片资源实例化不同数量的算法模块，仅需修改主控状态机，即可完成多模块的通信与配置，以此实现多任务并行计算。

其次，SM2 各模块间通过寄存器或FIFO 互连，具有松耦合架构，仅需替换快速模约减模块，即可实现NIST ECC 256、区块链中Secp256k1 等其他椭圆曲线算法。同时，本文实现了任意参数的SM2计算，适用范围更广。

最后，本文所有运算均在FPGA 内部实现，可配合哈希算法实现签名/验签、加解密和密钥交换等应用，且具有高效能计算的特点，可即插即用，灵活地应用在边缘设备的认证、云端服务、隐私保护等多种场合。

4 结束语

本文提出的可重构SM2 素域算法优化通过对SM2 各计算阶段的深入剖析，以软硬件协同的方式实现，在标准射影坐标系下优化并实现了蒙哥马利点乘、快速模乘、快速模逆和坐标系转换。同时，通过SM2 多模块并行，加速了数据的并行处理，可满足不同应用的计算需求。实验结果表明，该方法可重构出的SM2 算法在性能、资源等方面具有明显优势，较CPU 有352.48 倍以上的提升，并可扩展到签名/验签、加解密和密钥交换等功能，兼顾计算的高效性和灵活性。

下一步，将实现其他位宽的椭圆曲线的并行计算，通过对FPGA 进行合理布局划分，完成相应算法的切换和共享模块的使用，以获取更高的计算性能和适用范围。