Saturnin 算法的不可能差分分析

蒋梓龙，金晨辉

（信息工程大学密码工程学院，河南 郑州 450001）

0 引言

在NIST 轻量级密码标准竞赛中，Saturnin 算法[1]是进入第二轮的候选算法之一。算法设计者声称该算法不仅适用于小型电子设备，并且可以作为哈希和认证加密的基础算法。该算法在保持高效轻巧的同时具有极高的安全性，甚至可以抵抗量子计算分析。作为一个轻量级可抗量子计算分析的新算法，Saturnin 算法的安全性更值得深入研究。

不可能差分攻击[2-3]是差分攻击的一种特殊变体。与传统的差分攻击利用高概率差分对应完全相反，不可能差分攻击利用不可能出现的差分对应，即差分转移概率为0 的差分对应，来刻画算法的不完全随机性，并利用此信息泄露做区分攻击或者密钥恢复。关于不可能差分区分器的构造问题一直都是热点课题，在1999 年的FSE 会议上，Biham 等[2]详细地阐述了运用“中间相遇找矛盾”的方法构造不可能差分。后来随着自动搜索技术的出现，不可能差分区分器的构造变得更加高效精细，例如，Kim 等[3]提出的U 方法；Luo等[4]提出U 方法的改进版本，称之为UID 方法；Wu等[5]提出的线性化方法；Mouha 等[6]将混合整数规划（MILP，mixed integer linear programming）搜索用于差分分析。之后这类工具被广泛用于各类分析方法[7-9]，不可能差分区分器搜索与构造也是研究的热点，Cui等[10]首次利用MILP 求解不可能差分区分器；Sasaki等[11]系统详尽地阐述了如何利用MILP 方法搜索不可能差分；Hu 等[12]利用传播状态的特性，进一步改进了分析结果；张仕伟等[13]利用AND 组件特性，基于SAT求解器搜索到了更多的不可能差分区分器；Zhang等[14]提出了“模式运算”方法，实现了ARX 密码算法不可能差分区分器的自动化搜索。针对轻量级分组密码算法，也有不少关于不可能差分的分析结果，如武小年等[15]给出了GRANULE 算法的7 轮不可能差分区分器和MANTRA 的9 轮不可能差分区分器；王旭姿等[16]在相关密钥的条件下，首次给出了SIMON 算法的13轮不可能差分区分器。

Saturnin 是类AES 密码算法，分组长度为256 bit，由64 个4 bit 元胞构成。设计者声称针对AES 算法[17]的分析方法都可以用来分析Saturnin 算法，且Saturnin算法的安全性基础也受益于AES 的安全性结果。在设计报告[1]的第6 节中，基于在单密钥条件下的AES 安全性分析结果，设计者给出了Saturnin 算法抵抗经典攻击方法的安全性分析，包括差分攻击、线性攻击、代数攻击、不可能差分、中间相遇等分析方法。在攻击方案的安全性评估上，设计报告只给出了7.5 轮的中间相遇攻击方案；之后Hou 等[18]提出了用Yoyo 方法分析Saturnin 算法的攻击方案，但是Yoyo 需要自适应的明密文选择，分析方法所需要的条件较强。针对不可能差分，设计报告[1]中只给出了两条3.5 轮的不可能差分区分器，设计者声称“我们提出的2 个不可能差分区分器得到的攻击路径都需要攻击全部密钥比特。我们认为可能可以构造出4 轮或4.5 轮的攻击方案，但是至今我们也没有达成这个目标。”截至目前，只有设计报告[1]中给出了Saturnin 算法抵抗不可能差分的安全性分析，且设计者只给出了两条3.5 轮的不可能差分区分器，并没有给出完整的不可能差分攻击方案。为弥补这个缺项，本文对Saturnin 算法进行不可能差分分析，并提出了具体的5.5 轮不可能差分攻击方案。首先，基于Saturnin 算法的结构特性，本文提出并证明了3.5 轮不可能差分区分器的充分条件，即输入差分和输出差分非0 面（页）的个数和小于或等于4。利用此充分条件，可以快速构造270.1个不可能差分区分器，可以为攻击方案的设计提供更多的选择。之后，从构造的270.1个区分器中，有针对性地挑选了64 个区分器并分成了四类。将这四类区分器向前扩展2 轮各得一条攻击路径，这四条攻击路径不仅具有相同的明密文结构，且具有大量的公共密钥字节，利用这2 个特性可以改善攻击方案的整体复杂度。基于上述的四条攻击路径，结合一系列分析技术，本文提出了对Saturnin算法的5.5 轮不可能差分攻击方案。作为比较，设计者只构造了两条3.5 轮的不可能差分区分器，认为可能可以设计出4 轮或4.5 轮的不可能差分攻击方案，但他们也没有设计出相应的攻击方案。表1 总结了经典分析方法对Saturnin 算法的攻击结果。

表1 经典分析方法对Saturnin 算法的攻击结果

1 预备知识

1.1 符号表示

P：明文。

⊕：逐位异或。

Δx：x的差分值。

1.2 Saturnin 密码简介

Saturnin 算法是一个SPN 结构密码算法。算法的主密钥和中间状态都为256 bit，可以将主密钥和操作中间状态看作4 ×4 ×4个元胞的立方体，其中元胞代表一个4 bit 值。4 ×4 ×4个元胞的三维立方状态如图1 所示，立方状态中的元胞可以由三维坐标(x，y，z)表示位置，其中x，y，z∈{0，1，2，3}，对应的元胞号为(y+4x+16z)，元胞号为0～63，0 为最低有效位。举例而言，第33 号元胞的坐标为(0，1，2)。

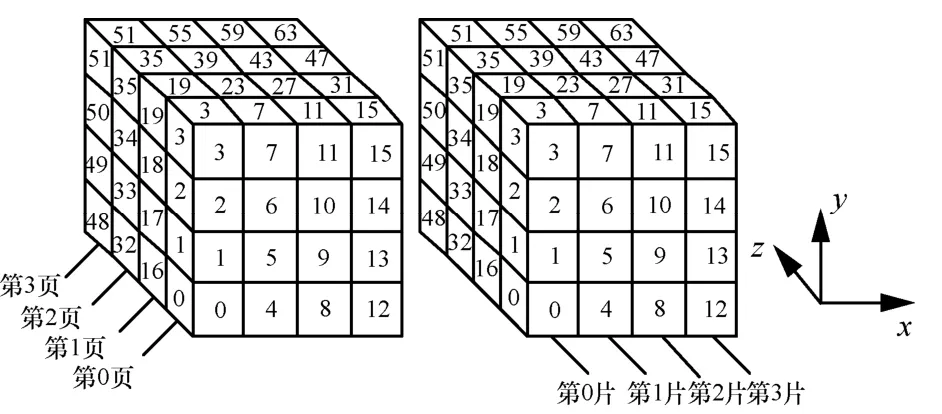
图14×4×4 个元胞算法的三维立方状态

根据Saturnin 算法的三维立方状态，本文定义了以下5 种立方状态中的子集。

1)页：在立方状态中，当z坐标值为固定值，x，y坐标值遍历，对应得到的16 个元胞集合为一页，记作第z页，符号表示为slice(z)。

2)片：在立方状态中，当x坐标值为固定值，y，z坐标值遍历，对应得到的16 个元胞集合为一片，记作第x片，符号表示为sheet(x)。

3)列：在立方状态中，当x，z坐标值都为固定值，y坐标值遍历，对应得到的4 个元胞集合为一列，记作第x+4z列，符号表示为column(x+4z)。

4)页行：在立方状态中，当y，z坐标值都为固定值，x坐标值遍历，对应得到的4 个元胞集合为一个页行，记作第y+4z页行，符号表示为xrow(y+4z)。

5)片行：在立方状态中，当x，y坐标值都为固定值，z坐标值遍历，对应得到的4 个元胞集合为一个片行，记作第y+4x片行，符号表示为zrow(y+4x)。

Saturnin 算法的设计者提出了合并轮[1]的概念。为方便阐述，本文中的一轮均指一个合并轮，加密算法的轮数从1 开始计数。用户可以输入2 个参数，分别为加密轮数R∈{10，…，31}和4 bit 的域分隔符D。算法默认加密10 轮，用户也可以在{10，…，31}中任选加密轮数。算法轮函数共包括6 种变换，分别为元胞替换S、页行移位变换SRs、片行移位变换SRt、列混合变换MC、轮子密钥加AK和轮常数加AT。这6 种变换简述如下。

1)元胞替换S。对立方状态中的全部64 个元胞做查S 盒的非线性变换。此变换由两类4 bit 的S盒构成，分别记作S0、S1，对元胞号为偶数的元胞查S0盒，对元胞号为奇数的元胞查S1盒。S0和S1如表2 所示。

表2 Saturnin 算法的两类4 bit 的S 盒

2)页行移位SRs。根据y坐标值进行页行循环移位操作，即在第y行按x坐标方向循环移位y元胞(y=0，1，2，3)，为SRs的逆变换。以第0 页为例，具体变换如图2 所示。

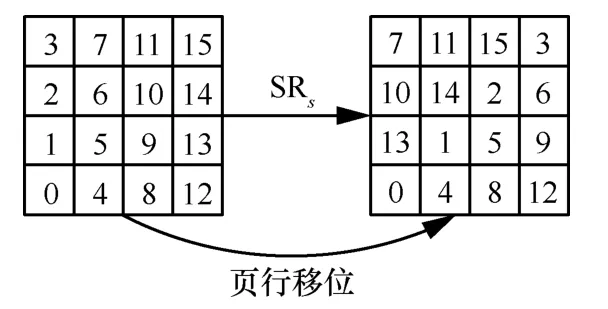
图2 Saturnin 算法的页行移位样例

3)片行移位SRt。根据y坐标值进行片行循环移位操作，即在第y行按z坐标方向循环移位y元胞(y=0，1，2，3)，为SRt的逆变换。以第0 片为例，具体变换如图3 所示。

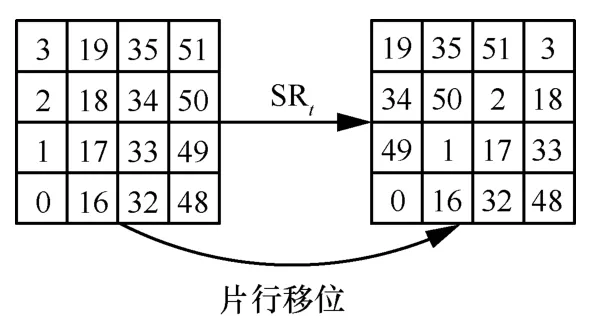
图3 Saturnin 算法的片行移位样例

4)列混合变换MC。对立方状态中的全部十六列做左乘变换M。

其中，α作用于4 bit 元胞。

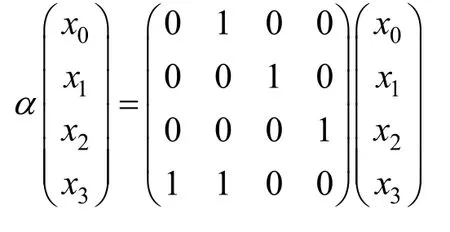
5)轮子密钥加AK。在每轮输出前进行轮子密钥加变换。记主密钥为64 元胞K0=(k0，…，k63)，对第i轮加密，若imod2=1，则用主密钥进行轮子密钥加变换；若imod 2=0，则将K0循环左移20 元胞，即用密钥K1=(k20，…，k63，k0，…，k19)进行轮子密钥加变换。算法开始时以K0为白化密钥，先对明文进行一次密钥加变换。

6)轮常数加AT。根据2 个输入参数（加密轮数R和域分隔符D），生成2 个16 bit 字RC0和RC1，再由RC0和RC1生成轮常数Ti，在第i轮输出前进行轮常数加变换。

Saturnin 算法的轮函数与轮号i有关。对第i轮加密，当imod2 ≡ 1时，轮函数为

当imod2 ≡ 0时，轮函数为

注意，白化密钥采用主密钥K0，需要先用K0与明文P做密钥加变换，即第一轮的输入为m0=P⊕K0，再调用轮函数进行加密。

关于Saturnin 算法的完整详细内容，可以通过查阅文献[1]做进一步了解。

2 Saturnin 密码的不可能差分区分器

为方便对差分路径进行阐述，2.1 节将轮函数进行简化，并给出状态、页、片和列的相关重量定义；2.2 节阐述Saturnin 算法3.5 轮不可能差分区分器的充分条件，并利用此充分条件构造了270.1个3.5 轮不可能差分区分器。

2.1 简化轮和立方状态重量

在单密钥且单常数的条件下，异或加不影响差分值。在忽略轮子密钥加和轮常数加变换的情况下，简化的轮函数也与轮数i(i＞ 0)有关。当imod2 ≡ 1时，轮函数为

当imod2 ≡ 0时，轮函数为

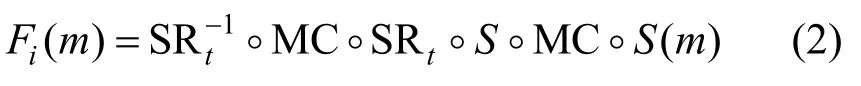
当轮号为奇数时，记简化轮函数为F1(m)；当轮号为偶数时，记简化轮函数为F0(m)。记F(st，r)(m)为从第st 轮开始加密r次简化轮，F-(st，r)(m)为从第st 轮开始脱密r次简化轮，其中st，r∈ {1，…，31}。例如，算法默认的10 次简化轮加密记为F(1，10)(m)=(F0◦F1(m))5。

由1.2 节可知，Saturnin 算法的立方状态m有4 个页、4 个片和16 个列，每个页、每个片分别有16元胞，每个列有4 元胞。对立方状态、页、片和列而言，元胞重量指包含的非0 元胞个数，元胞重量的符号定义为Wnibble。例如，Wnibble(mslice(0))=3表示在立方状态m的第0 页中有3 个非0 元胞。

若页、片、列的全部元胞值都为0，则元胞重量为0；反之元胞重量非0。对一个立方状态m而言，Wslice、Wsheet、Wcolumn分别表示在一个立方状态中重量非 0 的页、片、列的数量。例如，Wslice(m)=3表示在立方状态m中，重量非0 的页有3 个；Wcolumn(mslice(0))=3表示在立方状态m的第0页中，重量非0 的列有3 个。

2.23.5 轮不可能差分区分器的充分条件

基于中间相错的思想，本节用性质1 刻画Saturnin 算法3.5 轮不可能差分区分器的充分条件。

性质1在Saturnin 算法中，记输入差分为Δi n，经过3.5 轮加密后输出差分为 Δout。0.5 轮加密变换为在3 轮加密后再进行S◦MC◦S变换。根据起始轮轮号st 的不同，可得如下2 个3.5 轮不可能差分区分器的充分条件。

1)当st mod2 ≡ 1时，有

2)当st mod2 ≡ 0时，有

证明以 1)为例，证明充分性，已知Wslice(Δi n)+Wslice(Δout)≤4。

首先，因元胞替换和列混合变换不改变重量非0列的数量，故S◦MC◦S变换和对应的逆变换不会改变重量非0 页的数量和非0 片的数量，即可得Wslice(m)=Wslice(S◦MC ◦S(m))；因页行移位变换不改变重量非 0 页的数量，即可得Wslice(m)=Wslice(SRs(m))。又因F1变换中只包含页移位变换、元胞替换和列混合变换，故也不改变重量非0页的数量，即Wslice(m)=Wslice(F1(m))。则由上述分析可得，对∀Δ in′=S◦MC◦S◦F1(Δin)，都有Wslice(Δin)=Wslice(Δin′)；对∀Δout′=◦S-1◦MC-1◦S-1(Δout)，都有Wslice(Δout)=Wslice(Δout′)。

其次，因为Δout是由Δin经过变换S◦MC ◦S◦F1◦F0◦F1得到的。则可以推得在2 个立方状态 Δi n′=SRt(Δi n′)、Δ out′=SRt(Δout′)之间还存在一个列混合变换MC。

已知Wslice(Δ in)+Wslice(Δout)≤4，则由上述分析可得Wslice(Δi n′)+Wslice(Δ out′)≤4，即在2 个立方状态 Δi n′、Δout′中，至多存在4 个重量非0 页，则可得在2 个立方状态 Δi n′、Δout′中，同一片号i∈{0，1，2，3}下的两片 Δi n′(sheeti)、Δout′(sheeti)至多有4 个重量非0 列，不妨设为第0 片，则可得Wcolumn(sheet0)+Wcolumn(sheet0)≤4。对这两片Δin′(sheet0)、Δout′(sheet0)进行片移位变换SRt，可得 Δi n′′和Δout′第0 列的非0 元胞数最多为4 个，即W(Δin′column(0))+W(Δout′column(0))≤4，但这与列混合变换MC 的分支数为 5 矛盾，故Δi n3.5-roundΔout 成立。

性质1中2)部分的证明与上述类似。证毕。

由性质1 可知，Saturnin 算法的不可能差分区分器与输入和输出差分的非0 页数和非0 片数有关。以起始轮的轮号为奇数为例，统计Saturnin 算法3.5 轮截断式不可能差分区分器数量。

设x=(x0，…，x63)∈GF(24)64为Saturnin 算法的立方状态，令θ为GF(24)→GF(2)的映射，当xi=0时，有θ(xi)=0；当xi≠ 0时，有θ(xi)=1。则称χ(x)=χ(x0，…，x63)=(θ(x0)，…，θ(x63))为x的模式。

在立方状态中，存在一个差分非0 页时，共有A1=×(216-1)≈ 218个差分模式χ(x)；存在2 个差分非0 页时，共有A2=×(216-1)2≈234.6个差分模式χ(x)；存在 3 个差分非 0 页时，共有A3=×(216-1)3≈250个差分模式χ(x)。由性质1中充分条件的限制，通过排列组合，可以得到3.5 轮截断式不可能差分区分器个数分布，如表3所示。

表3 Saturnin算法截断式不可能差分区分器个数分布

将表3 的数据求和可得，由性质1 构造的3.5 轮截断式不可能差分区分器的个数约为270.1，设计报告[1]给出的两条不可能差分区分器也在这270.1个区分器之中。

为便于直观理解，令起始轮的轮号st 为奇数，输入差分 Δi n的非0 页数为3，输出差分 Δout的非0 页数为1。以上述输入差分 Δi n、输出差分 Δout为例，将性质1 构造的3.5 轮不可能差分区分器用图4 展示，其中最左侧的状态代表第0 页，从左至右的4 个状态分别代表第0 页至第3 页。在列混合变换MC 两侧，存在对应两列只有4 个差分非0 的元胞，这与列混合变换MC 的分支数为5 矛盾，故构成了截断式不可能差分区分器。

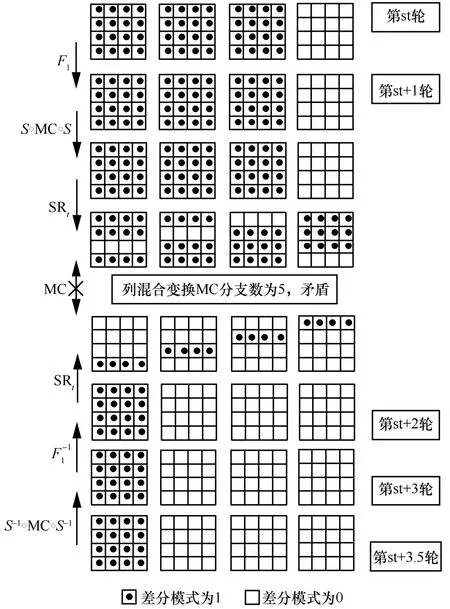
图4 Saturnin 算法的3.5 轮不可能差分区分器（起始轮号为奇数）

3 Saturnin 密码的5.5 轮不可能差分攻击

由性质1，令输入差分只有3 个非0 页，输出差分均只有一个非0 页，构造了四类从第3 轮到第5.5 轮的3.5 轮截断式不可能差分区分器。为方便阐述，本节以页行为单位，阐述区分器的截断差分及扩展攻击路径中的截断差分，并提出了页行的3 个状态：满页行状态、空页行状态和单页行状态。满页行状态指页行的4 个元胞差分值均非0；空页行状态指页行的4 个元胞差分值均为0；单页行状态指在页行中，有且只有一个元胞差分值非0，其余3 个元胞的差分值为0，且要求在一个状态中，单页行状态中差分值非0 的元胞都在同一片。

3.1 页行视角和四类区分器

由2.2 节可知，页行定义以页行为单位，则可以将Saturnin 算法看作由16 个页行组成。图5 展示了页行视角的Saturnin 算法状态，其中数字为页行号，从右至左分别代表第0 页至第3 页。

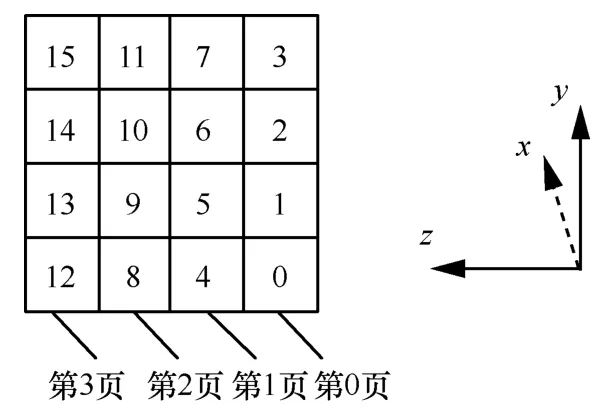
图5 页行视角的Saturnin 算法

本节由性质1 构造了从第3 轮至第5.5 轮的四类截断式不可能差分区分器。区分器的四类输入截断差分：每类输入差分各有4 个截断差分，即第i类区分器的第i-1片上有3 列共12 元胞差分非0，其余元胞差分为0，有4 种情况；区分器的四类输出截断差分：第i类区分器在第i-1页上共16 元胞差分非0，其余元胞差分为0。表4 展示了四类截断式不可能差分区分器的具体截断差分，其中的数字是4 个元胞差分值均非0 列的列号。表4中的任意输入/输出截断差分组合，都可构成3.5 轮不可能差分区分器，故一共有64 个不可能差分区分器，每一类分别有16 个不可能差分区分器。

设计者指出，他们提出的2 个不可能差分区分器，即使是扩展1 轮或0.5 轮，得到的攻击路径都需要攻击全部密钥比特，故设计者没有构造出相应的不可能差分攻击方案。为使构造的区分器能够适用于不可能差分攻击，本文特意选取了表4中的64 个区分器，这64 个区分器满足以下2 个特性。

表4 Saturnin 算法的四类3.5 轮不可能差分区分器

1)区分器输入差分有3 个非0 面，且在这3 个非0 面中，都有且只有一个非0 列；同时，这3 个非0 列都在一个页上。

2)区分器的输出差分有且只有一个非0 面。

将上述的64 个区分器分为四类，根据特性1)和Saturnin 算法的具体结构，构造了四条5.5 轮的不可能差分攻击路径，每条攻击路径都不需要攻击全部密钥比特。同时，本文仔细考虑了密钥生成算法，进一步减少了这四条攻击路径所需要攻击的密钥比特。

为便于直观理解，以第一个输入截断差分和第一个输出截断差分构成的不可能差分区分器为例，如图6 所示，以页行、元胞为单位，分别展示此不可能差分区分器样例。图6(a)是以页行为单位的截断差分示意，其中实心三角代表满页行状态，空心三角代表单页行状态，且此单页行状态中差分非0的元胞均在第0 片；图6(b)是以元胞为单位的截断差分示意。

图6 Saturnin 算法的3.5 轮不可能差分区分器样例

3.25.5 轮不可能差分攻击方案

基于3.1 节中的四类不可能差分区分器，只向前扩展2 轮，得到了四条5.5 轮的不可能差分攻击路径。由第i类区分器扩展的攻击路径记作第i条攻击路径，以图6中的第一类不可能差分区分器为例构造第一条攻击路径样例，利用图7 展示Saturnin算法的5.5 轮不可能差分攻击路径样例，其中，变换S◦MC◦S简记为MS，第一轮的子密钥加和常数加一起记为AKT1。在设计攻击方案时，先使用三条攻击路径只需要攻击9 列子密钥，第四条路径需要攻击10 列子密钥，即先使用需要攻击密钥较少的攻击路径，再利用攻击路径中的公共密钥信息，这样可以进一步改善攻击方案的整体复杂度。

图7 Saturnin 算法的5.5 轮不可能差分攻击路径样例

本节将变换S◦MC◦S整体看作一个非线性变换，即将其看作一列16 bit 的大S 盒，用16 个大S 盒并置构成了此非线性变换。攻击方案的攻击步骤包括预处理阶段、数据处理阶段和密钥筛选阶段3 个部分。

预处理阶段。为降低子密钥筛选阶段的时间复杂度，本节先对攻击过程中所需的计算存表，具体表的构造如下。

表Λ。对Saturnin 算法的16 bit 大S 盒，在给定非0 输入差分 Δin和非0 输出差分 Δout时，方程S(x)⊕S(x⊕Δin)=Δout平均可以求得一个解，构造表Λ 的索引为 (216-1)2个非0 差分(Δin，Δout)，每个(Δin，Δout)存储对应的方程解和对应大S 盒的输出(x，S(x))。

表Hi。对第i条攻击路径，在第一轮变换后，只有第i-1列和第i+3列中的8 个元胞差分非0，其余元胞差分均为0，共有 232个差分值对这 232个差分值做◦MC ◦SRs变换得到 232个差分值，将这 232个差分值存入对应的表Hi。

数据处理阶段。在明文的(8，9，10，11，12，13，14，15)这8 个页行位置取固定值，遍历其他8 个页行，可以得到 2128个明文，将其称之为一个明文结构。对每个明文结构下的 2128个明文，用快速排序技术[19]对明文做四次排序，即分别以密文的4 个页行(0，1，2，3)、(4，5，6，7)、(8，9，10，11)和(12，13，14，15)为指标排序，一共可以得到4 ×2128×(2128-1)÷2 ×2-192≈265个符合此攻击路径的明文对，将其存入表Ω中。本节选取个明文结构，故攻击方案中共有个明文对，可在四条攻击路径中重复使用。

密钥筛选阶段。为方便理解，本节以列为单位叙述密钥，如四条攻击路径中，所需要攻击的白化密钥K0为第0 列至第7 列密钥，记作K0，col(0，…，7)。四条攻击路径中所需攻击的第一轮子密钥K1分别为K1，col(0，4)、K1，col(1，5)、K1，col(2，6)和K1，col(3，7)，由Saturnin 算法的子密钥生成算法可知，其对应的主密钥分别为K0，col(5，9)、K0，col(6，10)、K0，col(7，11)和K0，col(8，12)，可以看出，除了第四条攻击路径，其余三条攻击路径中都有一列密钥与白化密钥相同，故前三条攻击路径中，只需要攻击9 列子密钥，共 2144bit子密钥。攻击方案按攻击路径的序号顺序进行子密钥筛选。以第一条攻击路径为例，用全部个明密对查表 H1得到密钥K0，再用K1部分加密看是否能得到区分器输入差分，若得到，则为错误密钥排除。若在子密钥K0，col(0，…，7)固定的情况下，全部216个第9 列子密钥K0，col(9)均为错误密钥，则当前子密钥K0，col(0，…，7)为错误密钥，予以排除，在后续的攻击路径中不需要再次检测子密钥K0，col(0，…，7)，从而改进了此阶段的时间复杂度。经过全部四条攻击路径的筛选后，剩余的候选密钥用加密验证排除错误密钥，直至恢复出正确主密钥。为方便阐述，◦MC ◦SRs简记为MR，密钥筛选阶段的具体步骤如下。将变换

步骤3由第二、三和四条攻击路径，利用对应的表Hi，进行与上述两步类似的筛选。在四条攻击路径都筛选完毕后，最后可以得到13 列中的候选密钥K0，col(0，…，12)。

步骤4穷举剩余的3 列子密钥K0，col(13，…，15)，即得到了全部主密钥，进行加密验证，直至得到最后的正确主密钥。

3.3 复杂度分析

预处理阶段复杂度相较整体攻击方案而言较少，可忽略不计。

数据处理阶段主要为明文加密得到密文的时间，故数据处理阶段的时间复杂度为次5.5轮加密。明文对只存储前两页的值，故所需的存储复杂度为算法规模。

密钥筛选阶段需要对四条攻击路径的复杂度进行分析。

第一条攻击路径筛选子密钥的复杂度分析如下。

第二步只需要在一片上进行部分加密计算，故认为其为0.25 轮加密。则第二步所需的时间复杂度为2128×2Ns-31×216÷(5.5 ×4)=次5.5 轮加密。由上述分析可知，对一条攻击路径而言，时间复杂度主要耗时在第二步。

下面分析经过第一条攻击路径筛选后，候选子密钥的个数。

由一条攻击路径可知，一个错误子密钥不通过一个有效明文对的检测概率是2-110，则一个错误子密钥通过一条攻击路径的检测概率是pL=。在第一条攻击路径中，经过个有效明文对的检测后，可得候选密钥的个数为2144×pL。

第一条攻击路径共涉及9 列密钥K0，col(0，…，7，9)。经过第一步的筛选，平均每个密钥K0，col(0，…，7)可以存储个中间状态对。在固定8 列密钥密钥K0，col(0，…，7)的条件下，K0，col(9)通过第一条攻击路径的检测概率为，则全部216个K0，col(9)都没有通过第一条攻击路径的检测概率为，Pk也是当前固定密钥K0，col(0，…，7)是错误子密钥的概率，故经过第一条攻击路径筛选后K0，col(0，…，7)的候选密钥的个数为 2128×(1-Pk)。

后三条攻击路径筛选子密钥的复杂度分析如下。

第一步均与第一条攻击路径的第一步相同。在第二步中，只需要攻击7 列白化密钥K0，col(0，…，7)中的候选密钥，故第二条攻击路径所需的时间复杂度为×(1-Pk)次5.5 轮加密；第三条攻击路径所需的时间复杂度为×(1-Pk)2次5.5 轮加密。由于第四条攻击路径在第二步需多攻击一列子密钥，因此第四条攻击路径所需的时间复杂度为×(1-Pk)3次5.5 轮加密。

加密验证阶段，即第四步，经过四条攻击路径的检测后，通过的候选子密钥个数为Nk=(2208-1)×(pL)4，需穷举 248子密钥K0，col(13，…，15)，故所需的时间复杂度为 248×Nk次5.5 轮加密。

4 结束语

本文对Saturnin 算法进行不可能差分分析。首先，提出并证明了Saturnin 算法3.5 轮不可能差分区分器的充分条件，利用此条件可快速构造270.1个截断式不可能差分区分器，从而为可以攻击方案的设计提供更多的选择。之后，构造了四类3.5 轮区分器，向前扩展2 轮得到了四条有相同的明文结构的攻击路径，利用这四条攻击路径，提出了Saturnin 算法的5.5轮不可能差分攻击方案，数据、存储和时间复杂度分别为2176.88个选择明文、2143.88算法规模和2176.91次5.5 轮加密，这是目前可见的对Saturnin 算法的一种不可能差分攻击方案。