一种基于正弦空间的数字阵列雷达波位编排技术

朱 伟，王 弼，贺 芃

(中国电子科技集团第三十八研究所，合肥 230088)

0 引 言

数字阵列雷达具备灵活的波束捷变能力，其目标搜索模式一般根据预先设置的雷达扫描波位和各个波位上的波束驻留，完成对被预警监视空域的覆盖。在考虑波束宽度随波束扫描变化而变化，且满足雷达目标截获性能要求的情况下，如何有效地完成探测空域的波位覆盖，合理利用雷达能量资源，是相控阵雷达搜索空域波位编排关注的重点。

在天线波束扫描过程中，数字阵列雷达天线远场波瓣图的半功率波束宽度和波束形状都会发生变化，尤其是对于相对铅垂线倾斜放置的天线阵面，搜索监视扫描波束编排更加复杂。针对波位编排问题，文献[1]提出了几种常用的波位编排方式，包括堆积波位和交叉排列波位等；文献[2]在研究波束展宽效应的基础上，说明了搜索波束在正弦空间坐标系下编排的必要性；文献[3]、[4]分别利用遗传算法和模糊规划等方法对雷达搜索波束驻留时间进行优化，以提高雷达搜索效率；文献[5]根据置信度和交接概率划分搜索空域，给出了一种以最大全局信息增益为准则的搜索波位动态编排方法；文献[6]利用椭圆方程，通过数值方法实现波位指向计算；文献[7]把复杂空域中边界的动态性和非线性难题转化为图论问题，提出了相控阵雷达最优波位编排的边界约束算法。以上方法计算量均较大。

本文根据相控阵雷达的基本原理，基于数字阵列雷达坐标系提出了一种主要针对雷达预警搜索空域的波位设计方法，利用三角转换及二次方程解算即可完成波位编排的快速计算。

1 数字阵列雷达坐标系

本文以倾斜的阵面为例将不同坐标系定义如下。

(1) 雷达直角坐标系

如图1所示，O为阵面中心点，阵面倾斜放置，γ为阵面倾斜角，基本平面与水平面平行，在基本平面内y轴指向阵面前方，x轴指向阵面平行方向，z轴与xy平面垂直指向上方。

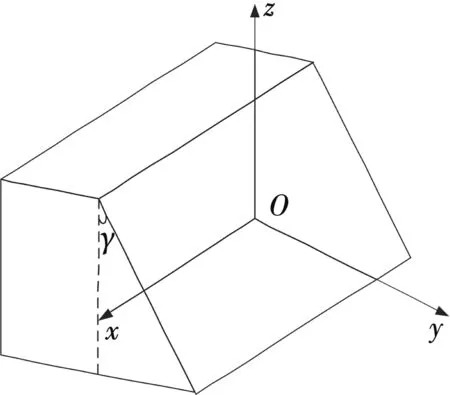
图1 雷达直角坐标系

(2) 雷达球坐标系

在雷达直角坐标系基础上可建立雷达球坐标系如图2所示，R为雷达阵面中心O到目标的距离，俯仰角φ为目标位置矢量与xy面夹角，方位角θ为目标位置矢量在xy面投影与y轴的夹角。

图2 雷达球坐标系

利用三角转换即可将雷达直角坐标系转换到雷达球坐标系，雷达直角坐标系的三维坐标(x,y,z)与雷达球坐标系的三维坐标(R,θ,φ)的转换关系为

(1)

(3) 阵面直角坐标系

阵面直角坐标系为雷达直角坐标系绕x轴旋转倾斜角γ，如图3所示，O为阵面中心点，y轴指向阵面垂直方向，x轴指向阵面平行方向，z轴沿阵面方向向上。

图3 阵面直角坐标系

利用三角转换即可将雷达直角坐标系的区域转换到阵面直角坐标系，雷达直角坐标系的三维坐标(x,y,z)与阵面直角坐标系的三维坐标(x′,y′,z′)的转换关系为

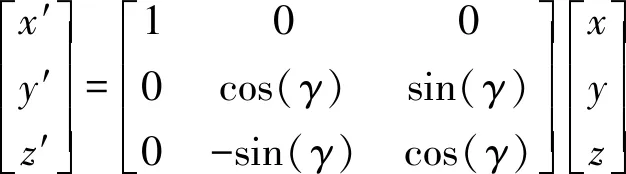
(2)

(4) 阵面球坐标系

在阵面直角坐标系基础上可建立阵面球坐标系如图4所示，R为雷达阵面中心O到目标的距离，俯仰角φ′为目标位置矢量与x′y′面夹角，方位角θ′为目标位置矢量在x′y′面投影与y′轴的夹角。

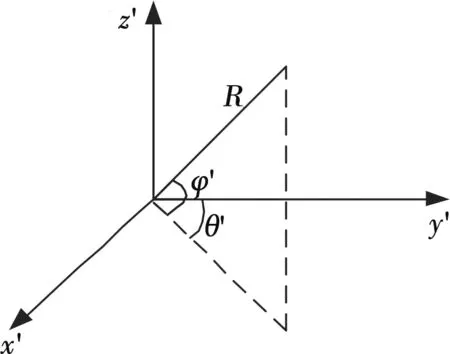
图4 阵面球坐标系

同上，阵面直角坐标系的三维坐标(x′,y′,z′)与阵面球坐标系的三维坐标(R,θ′,φ′)的转换关系为

(3)

(5) 正弦空间坐标系

在球坐标系研究阵列天线波束扫描时，扫描角偏离法线方向，波束将展宽，且展宽与扫描角间的关系非线性[2]，在球坐标系研究波束排列比较困难。而在正弦空间中，天线方向图不随扫描角变化，与扫描角成比例地平移，正弦空间就是单元球面在阵列平面上的投影[8]，如图5所示。

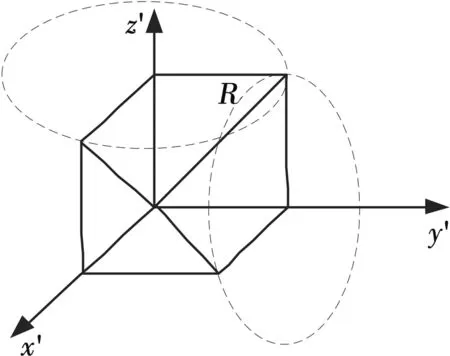
图5 正弦空间坐标系

将阵面球坐标系转换到正弦空间坐标系，阵面球坐标系的三维坐标(R,θ,φ)与正弦空间坐标系(R,u,v)的转换关系为

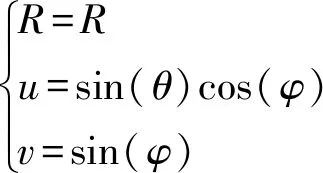
(4)

2 基于正弦空间的波束编排技术

正弦空间是把波束扫描三维球坐标空间通过正弦变换压缩到关于扫描角的二维正弦空间，仅保留了角度性质，与距离无关。正是由于相控阵雷达波束扫描特性，选择在正弦空间坐标系内设计相控阵雷达波位，可避免计算各个扫描角度上天线波束形状及宽度，从而降低搜索波位设计的复杂度。

以倾斜阵面为例，本文算法步骤如下：

(1) 计算天线阵面的法向方位波束宽度θ3 dB和俯仰波束宽度φ3 dB：

(5)

式中，λ为波长；NA为阵面水平阵元个数；dA为阵面水平单元间隔；NE为阵面垂直阵元个数；dE为阵面垂直单元间隔。

(2) 将方位波束宽度θ3 dB和俯仰波束宽度φ3 dB转换到正弦空间，为了同时对雷达工作频率进行归一化处理，在坐标转换公式中增加频率归一化，得到正弦空间U、V维波束宽度u3 dB和v3 dB：

(6)

(3) 将划定区域的范围由雷达直角坐标转换为雷达阵面坐标系。在雷达直角坐标系下划定的扇区范围区域示意如图6所示，以方位扫描范围-35°～35°、俯仰扫描范围15°～35°为例画图，可以看出在雷达直角坐标系下搜索范围为矩形区域。

图6 雷达直角坐标系下的搜索空域

将描述划定矩形区域的9个坐标点分别定义为坐标点0～8，其中坐标点0、2、6、8表示4个角，坐标点4表示区域中心，坐标点1、3、5、7分别表示4条边界线的中点。

站心坐标系坐标点0～8的坐标定义为(θ0,φ0)～(θ8,φ8)。9个点的坐标在图5中通过直角坐标系可直接获得。

将搜索区域由雷达直角坐标转换为雷达阵面坐标系，由于天线阵面具有一定的倾斜角，转换后的区域示意如图7所示。可以看出：在雷达阵面坐标系下搜索空域已经不是矩形范围，而是一个近似扇形的区域。

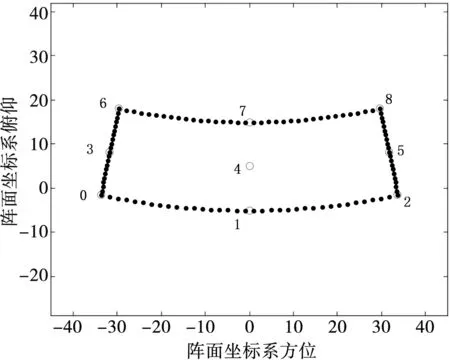
图7 雷达阵面坐标系下的搜索空域

阵面坐标系坐标点0～8的坐标定义为(θ′0,φ′0)～(θ′8,φ′8)，利用式(1)～(3)即可完成(θ0,φ0)～(θ8,φ8)到(θ′0,φ′0)～(θ′8,φ′8)的转换。

(4) 将转换后的阵面坐标系再转换为正弦空间坐标系，如图8所示。

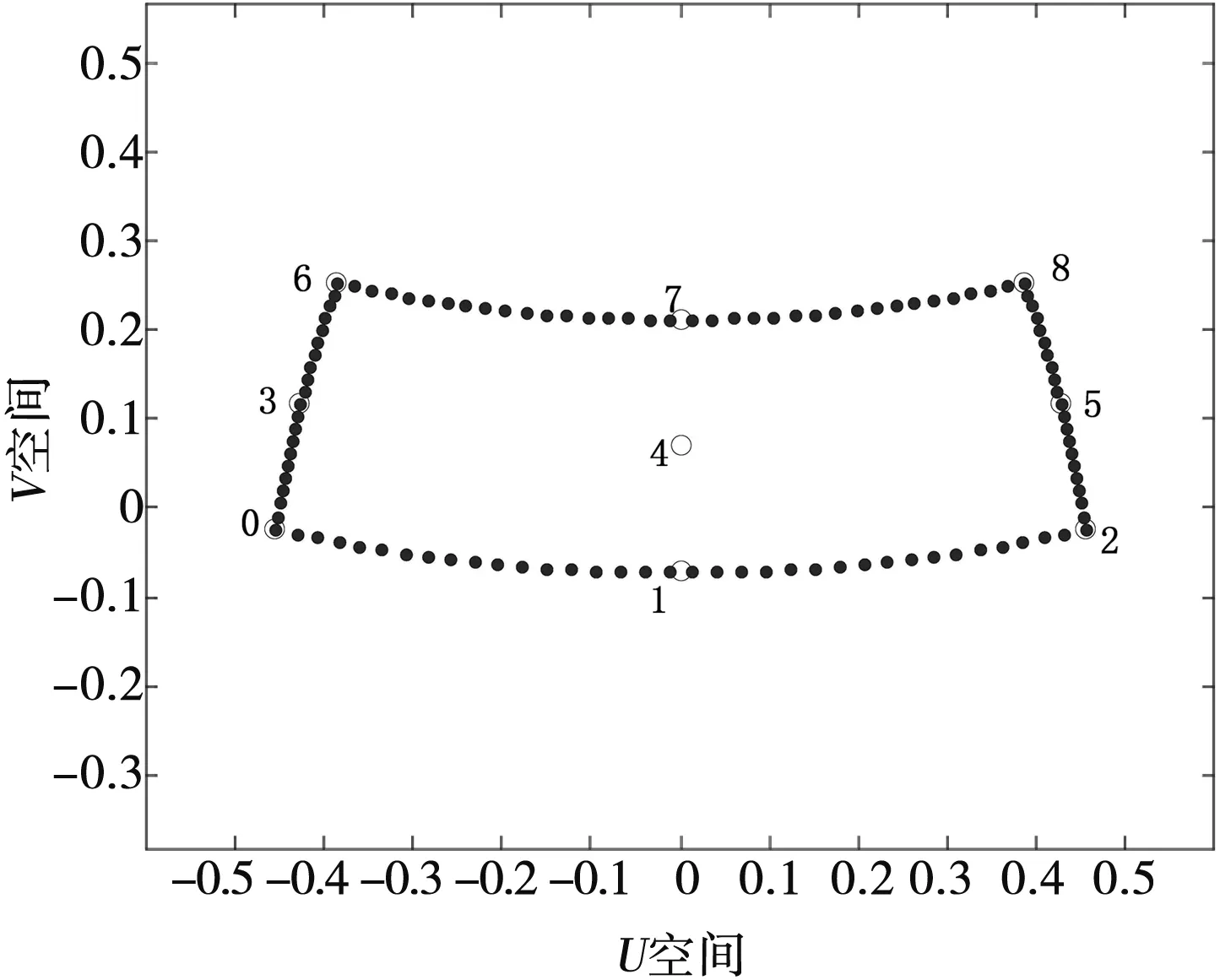
图8 正弦空间坐标系下的搜索空域

正弦空间下坐标点0～8的坐标定义为(u0,v0)～(u8,v8)。(θ′0,φ′0)～(θ′8,φ′8)到(u0,v0)～(u8,v8)的转换公式同式(6)，计算公式如下：

(7)

(5) 计算俯仰维度需要排列的波束个数，利用坐标点1和坐标点7计算正弦空间下V维度需要排列的波束数M：

(8)

式中，[·]为向上取整；J为交叠系数，当波束间1 dB交叠～波束间6 dB交叠时，J取值分别为0.567 4、0.730 8、0.884 9、1.009、1.114、1.205[2]；

在正弦空间下共需要排M行波束。

(6) 计算坐标点1～7之间排布波束在正弦空间中的纵坐标(即V维度值)，M个波束的纵坐标p(i)为

p(i)=v1+i·v·J,i=1,2,…,M

(9)

(7) 在每个纵坐标上对横坐标上的波束进行排列，由于在正弦空间下区域为近似扇形，不同的纵坐标下对应的横坐标波束数量不一样，排列过程如下：

(a) 分别利用坐标点0～2、坐标点3～5、坐标点6～8对正弦空间下区域的U维度边界弧线及中部弧线进行抛物线拟合，得到的抛物线方程分别为V=a1U2+b1U+c1、V=a2U2+b2U+c2和V=a3U2+b3U+c3，方程系数通过求解三元二次方程即可获得；

(b) 分别利用坐标点0、3、6和坐标点2、5、8对正弦空间下区域的V维度弧线进行抛物线拟合，得到的抛物线方程分别为V=a4U2+b4U+c4和V=a5U2+b5U+c5，方程系数通过求解三元二次方程即可获得；

(c) 计算沿着横轴方向穿过p(i)的抛物线，根据p(i)与v1、v7的位置关系计算得到的抛物线方程为

(10)

将式(10)简化为V=aiU2+biU+ci，其中

(d) 计算步骤(c)中得到的抛物线与步骤(b)中得到的两条抛物线的交点，得到左右交点的横坐标uL和uR分别为

(11)

(12)

(e) 计算横坐标uL和uR之间的抛物线弧长L(i)：

(13)

式中，zR=2aiuR+bi；zL=2aiuL+bi。

(f) 根据弧长L(i)计算第i行需要排列的波束数B(i)：

(14)

(g) 计算在uL和uR之间排布波束在正弦空间中的横坐标(即U维度值)，B(i)个波束的横坐标Bu(k)为

Bu(k)=uL+k·u3 dB·J,k=1,2,…,B(i)

(15)

(h) 计算B(i)个波束的纵坐标(即V维度值)Bv(k)：

Bv(k)=aiBu(k)2+biBu(k)+ci,k=1,2,…,B(i)

(16)

得到第i行的第k个波束的正弦空间指向为(Bu(k),Bv(k))。

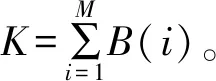
编排的各波束在正弦空间的指向示意如图9所示，其中“+”为正弦空间下的波束指向。

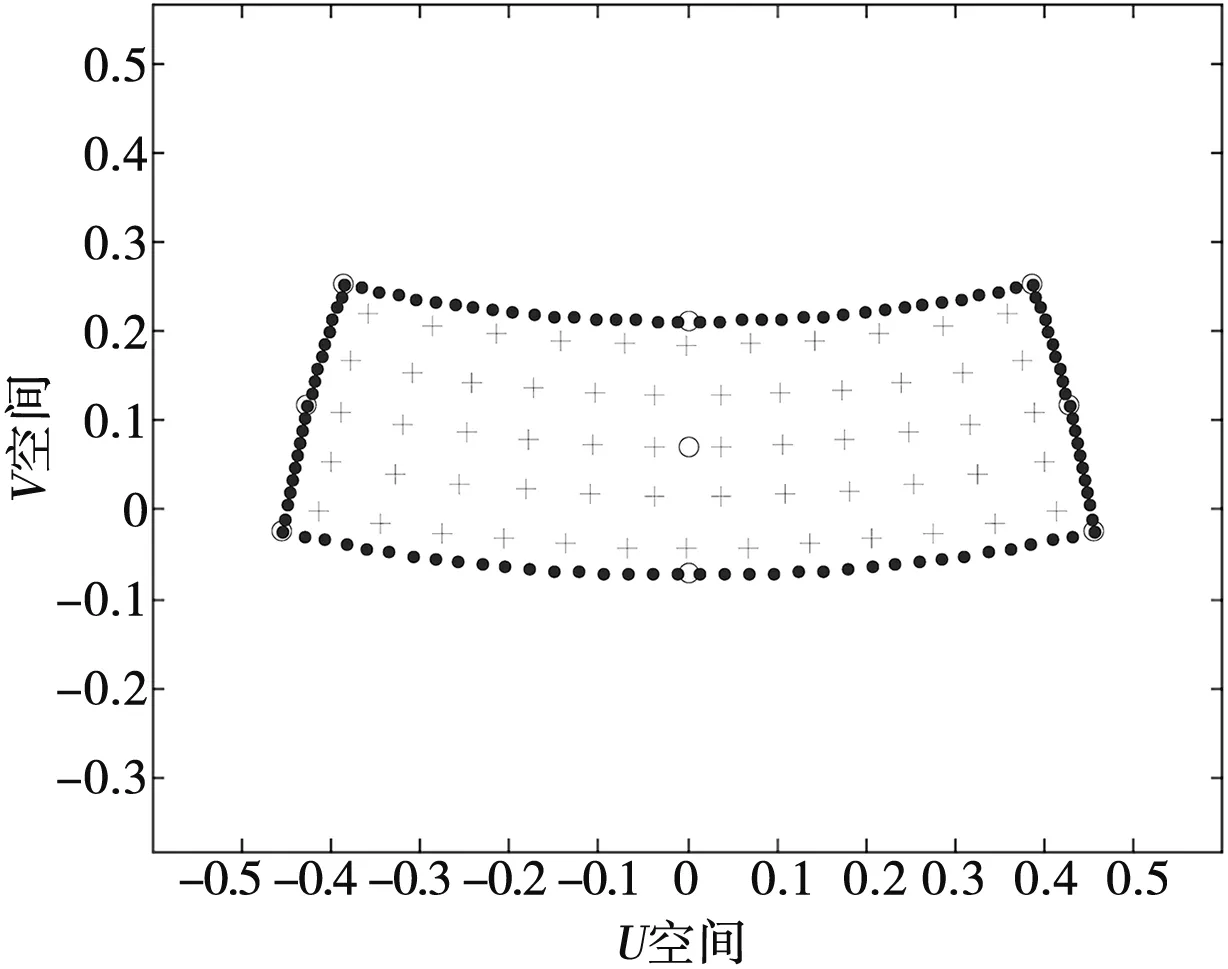
图9 正弦空间坐标系下搜索空域

(j) 根据在正弦空间坐标系下得到的K个指向转换到阵面坐标系的K个指向，转换公式如下：

(17)

上述计算主要为三角变换和二次方程求解，所有计算均有闭式表达式，可以看出算法运算量很小。

3 仿真效果

对本文算法进行计算机仿真，假设雷达阵面为水平22个阵元，垂直22个阵元，波长为1 m，水平间距为0.5倍波长，垂直间距为0.45倍波长。搜索区域的仿真条件：方位范围-35°～35°、俯仰范围15°～35°，波束间交叠系数为0.884 9。

堆积波束算法、考虑波束展宽的交叉排列波束算法和本文算法的仿真效果分别如图10～12所示，其中“+”表示波束中心指向，每个圆圈表示波束覆盖范围。

图10 堆积波束算法的波束编排图

图11 交叉排列波束算法的波束编排图

可以看出：3种方法均能完成搜索空域覆盖，堆积波束、交叉排列算法和本文算法的波束编排个数分别为70、65、61，覆盖同样的区域，本文算法需要的波束较少，可提高搜索数据率。

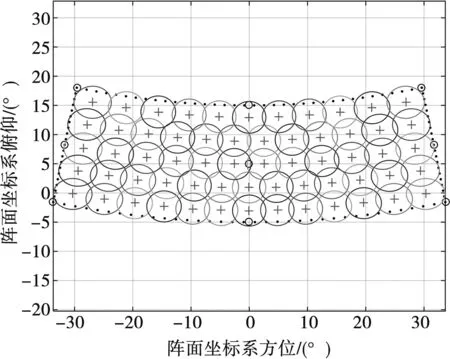
图12 本文算法的波束编排图

4 结束语

搜索区域内良好的波位设计是实现快速有效发现目标的重要条件之一，利用最少波束完成空域覆盖能最优利用雷达搜索资源。本文利用正弦空间内天线波束宽度不变的特性，提出了一种针对雷达预警搜索区域波位编排设计方法，通过三角变换和二元方程求解即可实现波束指向的快速计算。仿真结果表明：本文算法在完成搜索空域覆盖的同时，有效减少了所需波位数量，节省了系统资源，提高了搜索数据率。