基于LOSPA的雷达多目标跟踪性能评估技术
2022-03-31王曙曜班阳阳
闫 龙,王曙曜,班阳阳,姚 远
(中国船舶集团有限公司第八研究院,南京 211153)
0 引 言
传统的多目标跟踪性能评估方法一般借助于势差评价指标集合和状态精度指标集合对系统输出的航迹状态与目标真实状态的接近程度进行评价[1]。势差评价指标主要通过目标估计状态集合和目标真实状态集合之间的势的差异对跟踪性能进行评估,包括虚假航迹比例、冗余航迹比例、航迹交换次数、航迹中断次数等。状态精度指标则通过目标估计状态集合和目标真实状态集合元素之间的差异对跟踪性能进行评估,包括航迹起始延迟、航迹终止延迟、均方根误差、均欧式误差、均调和误差和均几何误差。传统的性能评估方法存在以下问题:一是具体使用时指标集合的选择问题,二是如何联立指标集合形成最终量化的问题。由于有些指标间存在相关性和矛盾性,这两个问题尚没有明确且被广泛接受的结论。
鉴于传统评估方法存在的问题,许多学者试图建立一种直观且具有明确物理意义的“数学距离”作为综合度量对多目标跟踪性能进行整体评价[2]:Hausdorff距离[3]首先被证明是有效的多目标跟踪性能评估方法且得到了实际应用,然而Hausdorff距离存在对离群值惩罚过重、对集合势之间的差异不敏感等缺点;为了克服Hausdorff距离上述缺点,基于最优质量转换(Optimal Mass transfer,OMAT)距离[3]被提出,部分解决了集合势差之间不敏感的问题,但是没有明确的物理意义,且存在几何依赖特性等缺陷;针对以上不足,最优子模式分配(Optimal Sub-Pattern Assignment,OSPA)距离[4]、标记最优子模式分配(Labeled Optimal Sub-Pattern Assignment,LOSPA)距离[5-6]相继被提出,其中LOSPA距离在OSPA距离考虑态势差异和状态精度差异的基础上引入了航迹标记差异,是目前被广泛接受的适用于多目标跟踪性能评估的综合度量[7]。
1 OSPA距离性能评估方法
(1)
式中,x,y∈N;1≤p≤∞。
也可以采用马氏距离进行描述,即
(2)
式中,S为x、y之间的协方差矩阵。
定义两点之间的截断距离为
dc(x,y)=min{c,d(x,y)}
(3)
式中,c为截断参数。
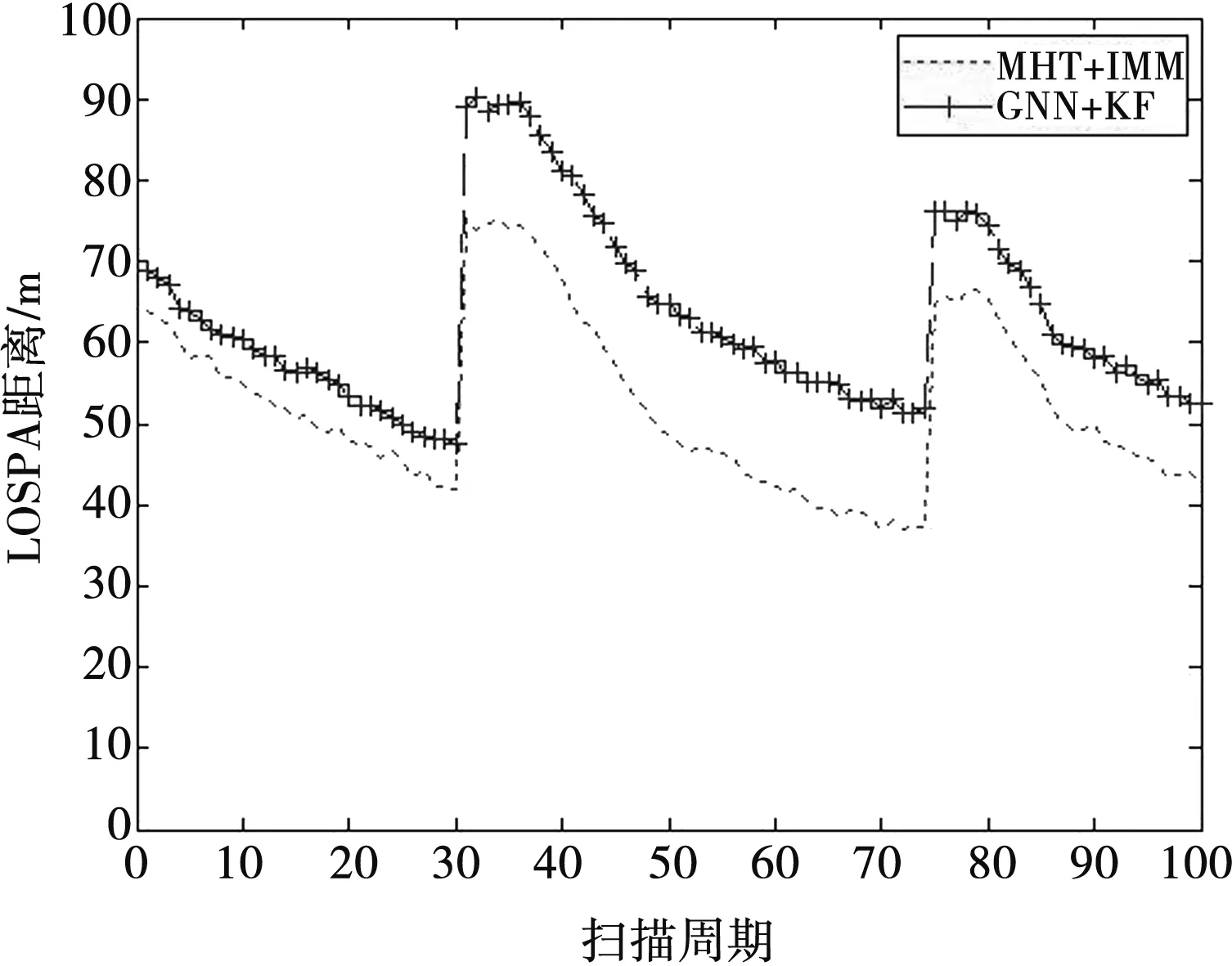
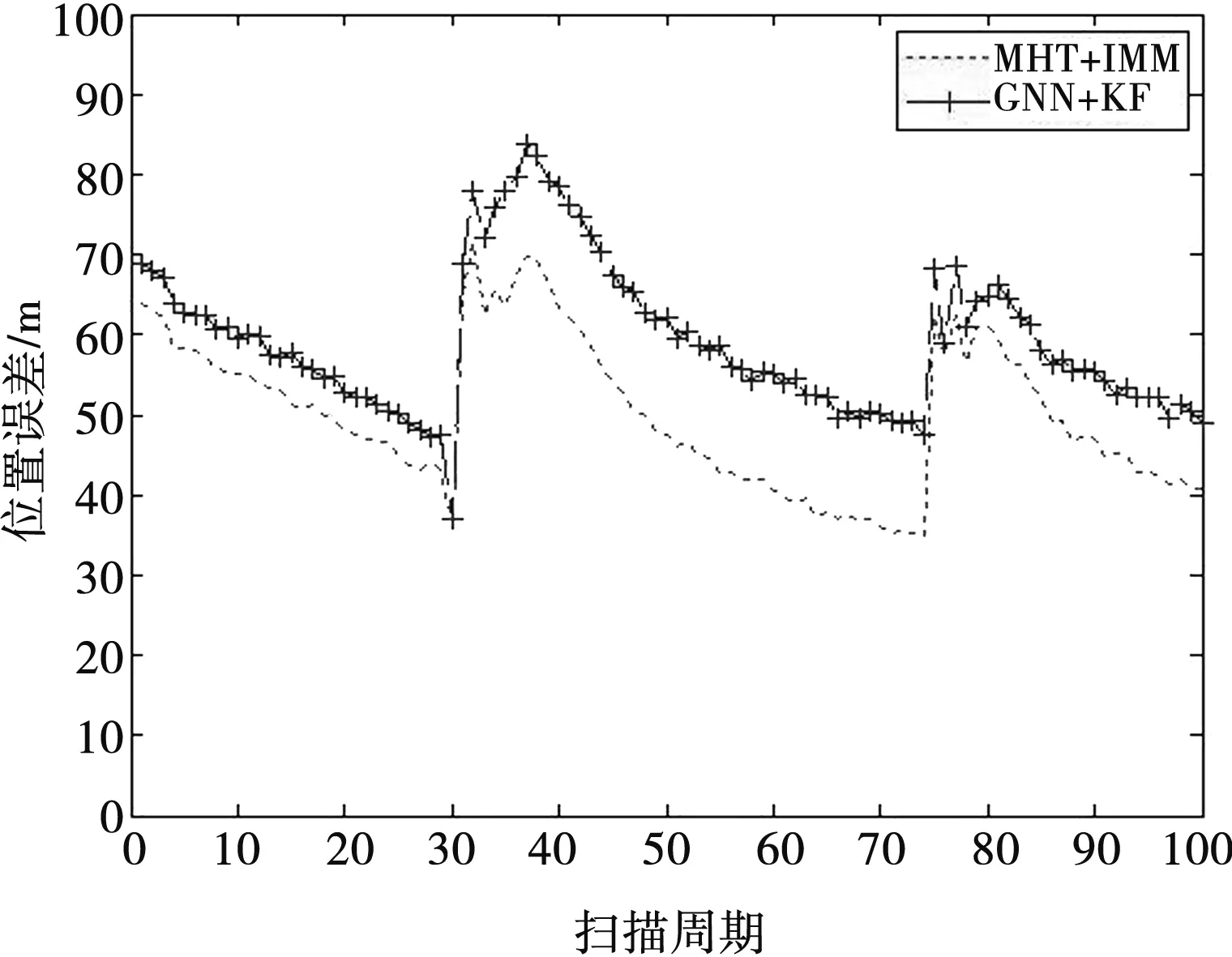
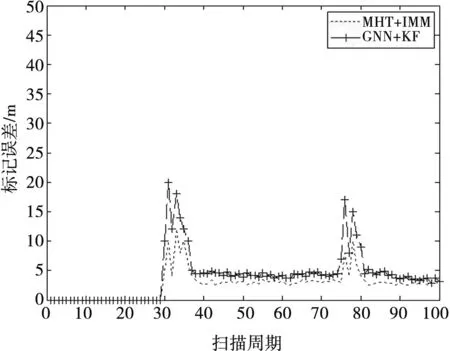
假定目标估计状态集合为X={x1,x2,…,xm},目标真实状态集合为Y={y1,y2,…,yn},n,m∈0={0,1,…}代表在同一扫描周期内的目标估计数目和目标真实数目。若m (n-m)cp)]1/p (4) 式中,∏n为从{1,2,…,n}集合中选择m个数的所有排列组合。 若p=1,可以将OSPA距离表示为 (5) (6) (7) 位置差异反映了实际空间距离差,势差异反应了虚假航迹比例、冗余航迹比例、航迹中断次数等性能参数。截断参数c反映了位置差异和势差异之间的权重,参数c越小,位置差异权重越大。 对于m>n的情况,只须将式(4)、(6)、(7)中的n和m互换即可。 (8) (9) 式中,s、t为集合标记;x∈X;y∈Y。 对于m (10) (11) 式中,δ(s,t)为狄拉克函数,当s=t时δ(s,t)=1,否则δ(s,t)=0;α为两集合标记差异权重系数。 (12) (13) (14) (15) =0.5 (16) n-m=1 (17) 联立式(15)~(17),最终计算出两集合的LOSPA距离为0.83。 (18) 利用二维分配矩阵将目标估计航迹t和目标真实航迹s进行关联,将目标估计航迹t赋值为s。在明确目标估计航迹标记后,利用式(8)~(11)计算每个扫描周期内目标真实航迹状态和目标估计航迹之间的LOSPA距离。 在仿真场景中设置3批目标T1、T2、T3分别从(0,40 000)、(32 000,40 000)和(16 000,54 000)处开始运动,经过直线交会、6 g加速度转弯、并排前进、4 g加速度转弯和直线分离等过程。目标高度分别为25 m、50 m和75 m,航速300 m/s,真值态势如图1所示。 图1 真值态势图 假设雷达探测目标距离测量误差100 m,方位测量误差0.2°,仰角测量误差0.2°,扫描周期2 s,探测概率0.9。叠加非异常杂波点分布为5 km×5 km×1 km的空间里小于3个杂波点。某次蒙特卡罗仿真试验中的量测态势如图2所示。 图2 量测态势图 针对仿真态势,采用全局最近邻算法(Global Nearest Neighbor,GNN)和标准卡尔曼滤波(Kalman Filtering,KF)算法进行关联滤波,跟踪效果如图3所示。采用多假设跟踪算法(Multiple Hypothesis Tracking,MHT)和交互多模型(Interacting Multiple Model,IMM)算法进行关联滤波,跟踪效果如图4所示。 图3 GNN+KF跟踪效果 图4 MHT+IMM跟踪效果 进行100次蒙特卡洛仿真,设定LOSPA距离计算参数p=1,c=100,α=50,根据式(8)~(11)的具体实现方法,分别计算两种跟踪算法的LOSPA距离,计算结果如图5所示。 图5 两种跟踪算法的LOSPA距离 根据式(12)、(13)分别计算两种跟踪算法的位置误差和标记误差,结果分别如图6、图7所示。可以看出,在交叉之前、并行前进和最后分离的直线运动中两种跟算法的LOSPA距离、标记误差和位置误差基本一致,由于MHT算法考虑了历史点迹的影响,关联更准确,IMM滤波算法的交互融合使航迹更为平滑,因此MHT+IMM跟踪算法的LOSPA距离和位置误差略小。交叉时两种跟踪算法的LOSPA距离、标记误差和位置误差瞬时增大,GNN+KF跟踪算法在交叉时出现了误关联,导致目标T1和T2丢失,出现航迹冗余、航迹中断等计算因子,因此LOSPA距离和标记误差增大,明显高于MHT+IMM跟踪算法的跟踪结果,且位置误差略高于后者。当6 g和4 g加速度转弯时,MHT+IMM跟踪算法的关联正确率更高、滤波更平滑,LOSPA距离、标记误差和位置误差明显小于GNN+KF跟踪算法。 图6 两种跟踪算法的位置误差 图7 两种跟踪算法的标记误差 由理论分析和经验可知,MHT+IMM跟踪算法在杂波环境下多目标跟踪的效果明显优于GNN+KF跟踪算法。仿真结果与算法本身的跟踪性能基本一致,验证了本文基于LOSPA距离的雷达多目标跟踪性能评估方法的有效性。 基于LOSPA距离的雷达多目标跟踪性能综合度量评估方法具有严格的数学理论依据、明确的物理意义,而且实现简单、表达准确、结果直观。本文详细论述了LOSPA距离的理论推导和计算方式,并在此基础上设计了针对雷达多目标跟踪性能评估的具体实现方法。通过对比GNN+KF和MHT+IMM两种跟踪算法对仿真目标进行跟踪的效果,利用LOSPA距离评价两种跟踪算法的性能,验证了LOSPA距离在雷达多目标跟踪性能评估中的有效性。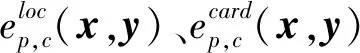
2 LOSPA距离性能评估方法
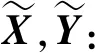
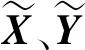
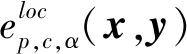


3 应 用
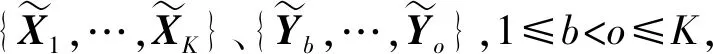

4 仿真试验
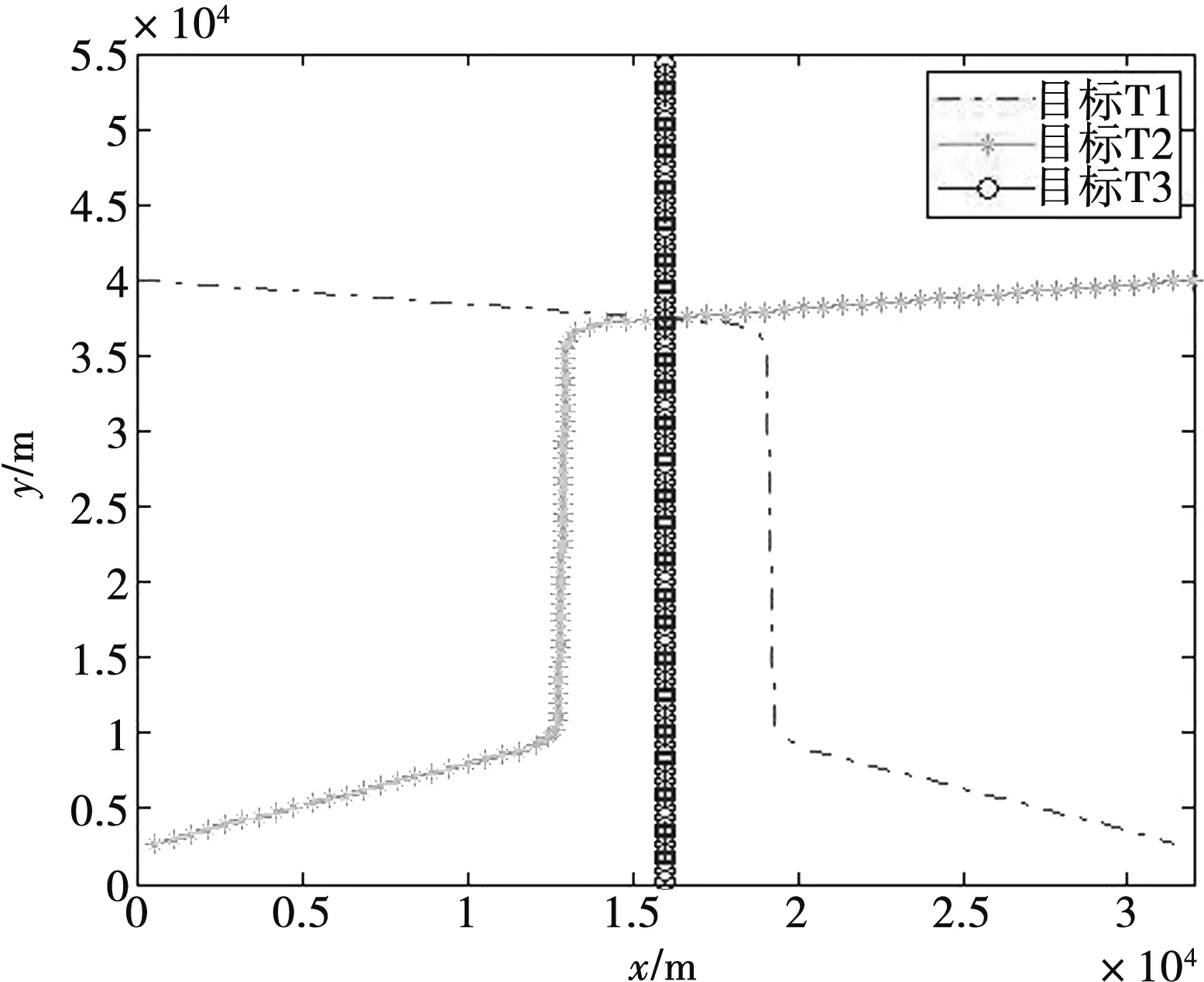
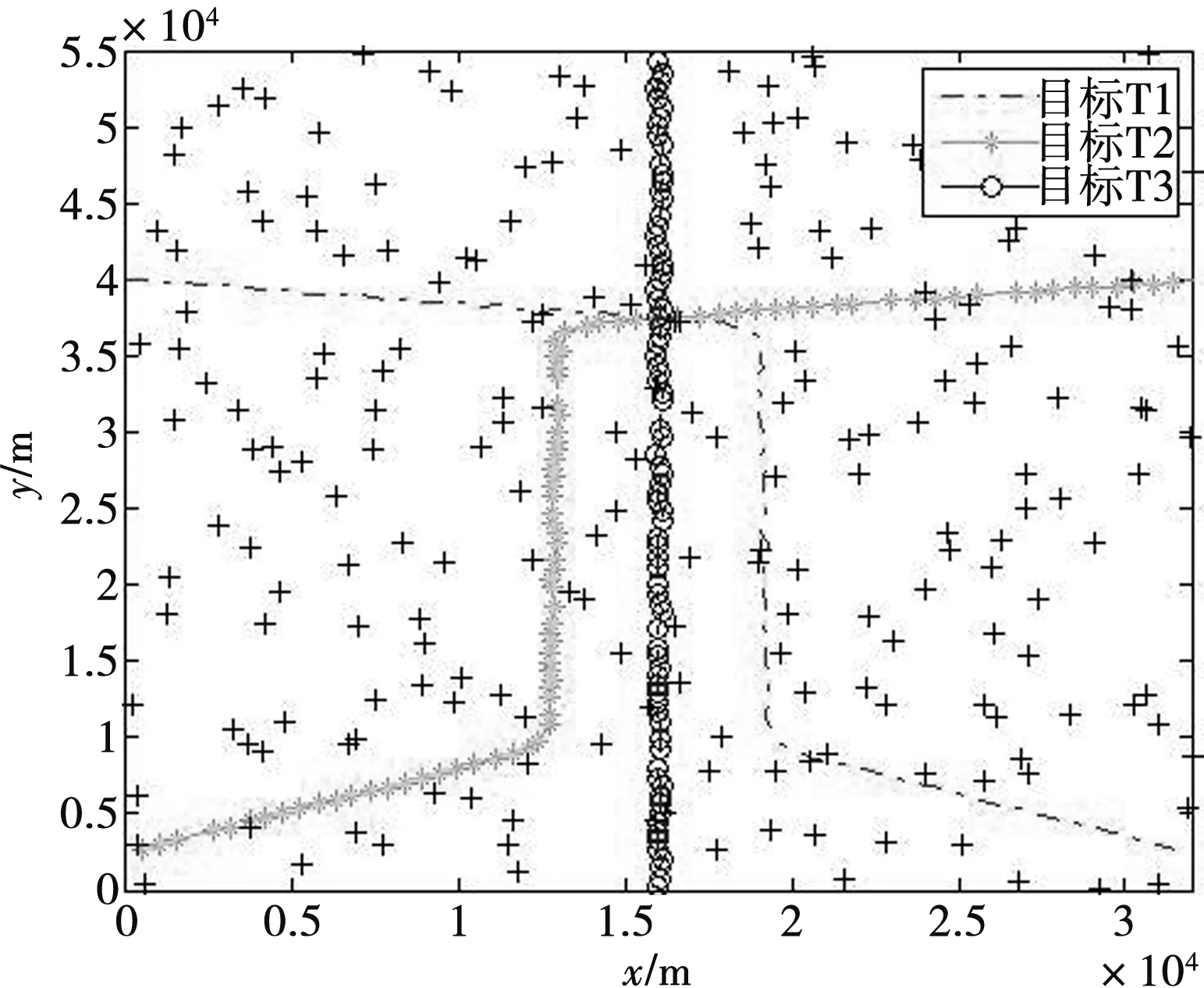

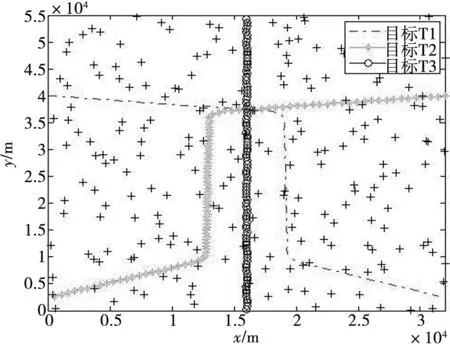
5 结束语
