一种汽车雷达系统中速度解模糊的工程实现方法

熊丁丁，李栋梁,2

(1. 中国电子科技集团公司第三十八研究所，合肥 230088；2. 汽车智能网联与主动安全技术国家地方联合工程研究中心(安徽)，合肥 230088)

0 引 言

由于汽车行驶环境复杂多变，汽车雷达系统对目标车辆的测速范围要求较高，模糊速度解算是汽车雷达系统设计中不可或缺的一项任务。

为了实现准确的距离速度参数估计，国内外许多研究机构对此开展了相应研究：文献[1]采用频谱配对方法获得无模糊的距离和速度估计，但是该方法的目标配对单靠上下扫频频谱面积来确定， 不能分辨处于同一距离但速度不同的目标，难适应大量目标的场合；文献[2]采用MTD-频域配对法来实现配对及距离速度去耦合，虽然通过MTD简化了目标环境，提高了雷达的分辨能力，但其利用目标上下扫频频谱峰值来实现配对的算法较为复杂，对于具有相似反射强度和频谱形状的不同目标很难配对，不能适应较为复杂的目标环境；文献[3]提出了一种利用运动目标在上/下扫频段频谱的对称性，并结合各个目标模糊多普勒速度的差异，实现上/下扫频段目标的准确配对及距离速度去耦合的方法，该方法对上/下扫频段均须进行目标检测，计算量大，且在目标高速运动的情况下容易出现配对错误，不易于工程实现。

为了能适用于汽车雷达系统工程实现，本文采用单发多收的雷达系统，设计一种特殊的变周期组合波形，并基于参差重频解速度模糊的理论，提出一种可便捷修改最大探测速度范围的工程实施方法。该方法可以对汽车雷达背景下的高速运动目标实现准确的速度估计，并补偿多普勒频移引起的距离偏移，可以提高测距精度和测速范围，同时在多目标情况下可实现同距离不同速度和同速度不同距离的不同目标的模糊速度解算。

1 信号模型

考虑一个单发多收的汽车雷达系统，系统模型如图1所示，假设发射天线T位于坐标原点o(0,0)，M个接收天线沿x轴等间隔分布，相邻天线间间距为λ/2，其中λ为发射信号波长，λ=c/f0。雷达发射载频为f0的线性调频连续波s(t)，其第k周期发射信号的时域表达式为

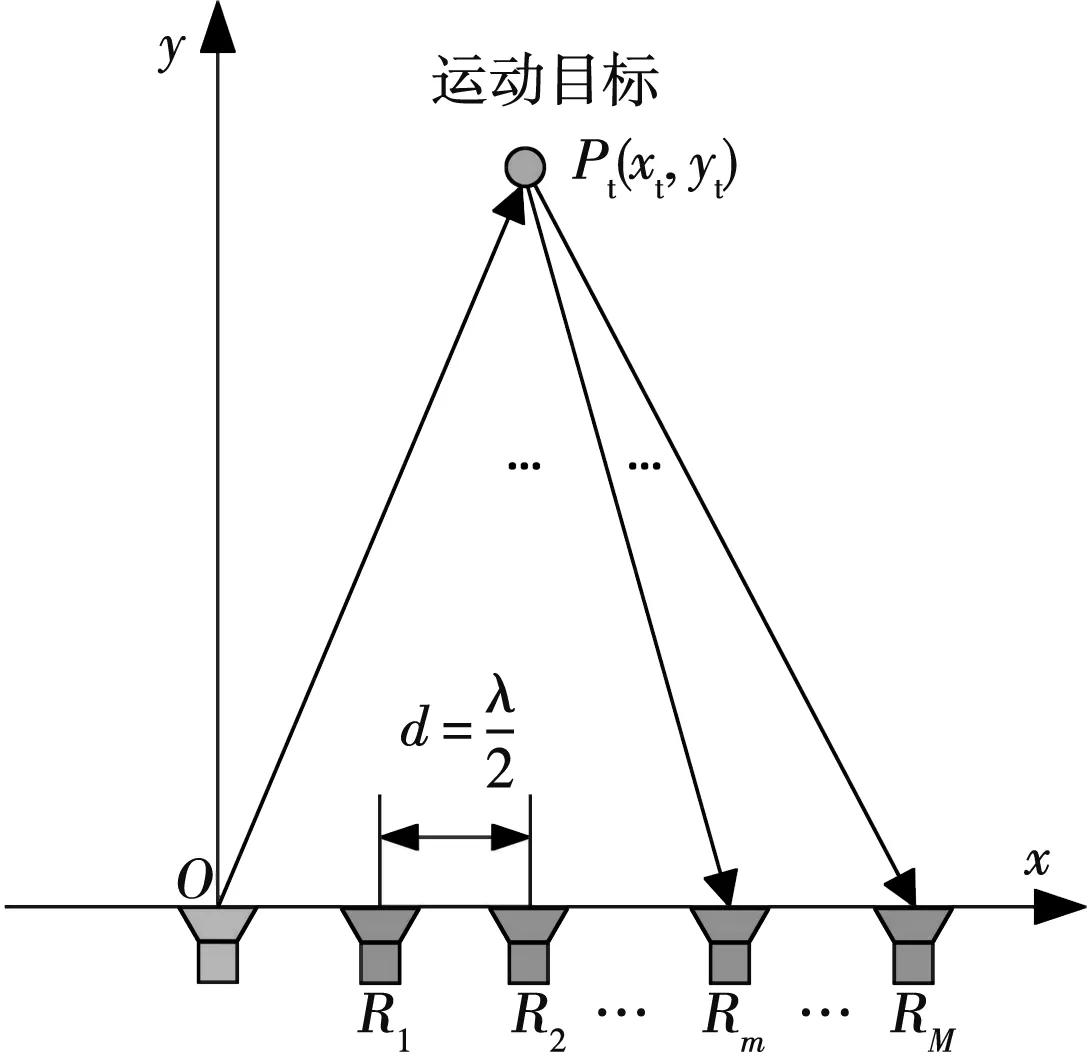
图1 单发多收雷达模型

sk(t) =A0exp(j2πf0t+jπμt2)u(t)，

k=1,2,…,K

(1)

1.1 目标模型

以运动目标如汽车、自行车等为例进行分析，假设目标位于远场，看作点目标。假定目标模型为

R(t)=R0+vt

(2)

式中，R0为目标初始距离(t=0)；v为目标径向速度(远离雷达为正)。

目标的瞬时回波延迟为

τ(t)=2R(t)/c=τ0+2vt/c

(3)

式中，τ0=2R0/c为目标初始延时时间。

对于第i个接收天线，第k周期的目标回波可以表示为

xi,k(t)=KriA0exp{j2πf0[t-τ(t+kT)]+

jπμ[t-τ(t+kT)]2}，

i=1,2,…,N；k=1,2,…,K

(4)

式中，Kri为反射后回波幅度衰减系数；τ(t+kT)=τ0+(2v/t)(t+kT)为第k周期发射信号的回波延时。

1.2 回波模型

考虑噪声时，第i个接收天线的总回波表示为

yi,k(t)=xi,k(t)+z(t)

(5)

式中，z(t)为噪声。

将回波信号与发射信号混频和低通滤波，化简后得到差拍信号为

exp(j2π(fd+μτ0)t)×

exp(j2πfdkT)]+z(t)

(6)

式中，fd=2v/λ为由目标运动引起的多普勒频率。

δ(wR-2π(fd+μτ0))

(7)

可以看出，距离谱峰值出现在频率wR=2π(fd+μτ0)处。由式(7)可以得到测量距离表达式为

(8)

说明在运动目标的测距测速过程中，多普勒效应会引起多普勒距离速度耦合现象。距离速度耦合是指对动目标测距时，多普勒效应导致测得的距离与真实距离存在偏差，偏差距离与多普勒频移相关[6-7]。因此，为了正确探测目标的距离，需要先探测目标的运动速度。对式(6)在慢时间维对kT做FFT，可以得到目标的速度谱：

δ(wv-2πfd)

(9)

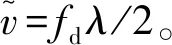
2 速度解模糊

2.1 波形设计

为了在工程应用中实现速度解模糊和距离速度解耦合，本文提出了一组特殊的变周期波形设计方法：发射两组调频带宽B和调制时宽T均一致的波形，仅通过改变相邻脉冲间的休止期Tr来改变脉冲重复时间。本文简称为AB波，其波形时序如图2所示，其中T为有效时宽，Tr1为A波休止期(包括频率恢复时间)，Tr2为B波休止期，K为脉冲重复周期数，B为射频信号带宽，Tf为帧重复周期。

图2 AB波波形时序示意图

当回波信号在快时间维的采样点数为L时，系统的理论指标为

(10)

式中，ΔR为距离分辨率；Rmax为理论上不模糊距离范围；Δv为速度分辨率；Vmax为最大不模糊速度范围。

当发射信号为A波时，Tp1=T+Tr1，对应速度分辨率Δv1和最大不模糊速度Vmax1；当发射信号为B波时，Tp2=T+Tr2，对应速度分辨率Δv2和最大不模糊速度Vmax2，因此A波和B波具有不同的速度分辨率和最大不模糊速度范围。

2.2 实现方案

假设目标对应A波和B波的速度维频谱峰值模糊索引分别为kA和kB。由于A波和B波的信号带宽一致，距离分辨率一致，由式(8)可知，目标对应A波和B波的距离维频谱峰值的速度距离耦合索引lA=lB，即同一目标在A波和B波的距离维索引是一致的，可以在信号处理过程中避免B波的目标检测过程，进一步减少计算量，提高雷达系统的实时性。

由上述分析可知，目标在A波的二维回波矩阵K×L维(K为每个接收通道的总的回波数，L为每个回波信号的采样点数)中对应的坐标分别为(kA，lA)，峰值幅度为PA。由于lA=lB，可以提取出B波的二维回波矩阵中lB对应的目标速度维频谱向量KB∈K×1。

以A波为基准进行速度解模糊。A波对应的速度分辨率Δv1和最大测速范围为[-Vmax1，Vmax1]，假设速度范围放大系数为正整数C，可根据测速要求范围进行灵活调整，对应的速度解算范围为[-Vmax1-C×2Vmax1，Vmax1+C×2Vmax1]，对应的速度解算索引为-C,-C+1,…,0,…,C-1,C。

AB波速度解模糊具体过程如下：

步骤1：针对不同的速度解算索引Ci，计算目标模糊索引kA对应的可能速度值vi：

vi=kA×Δv1+Ci×2Vmax

(11)

步骤2：根据得到的vi计算出目标速度在B波对应的理论速度索引k′B=vi/Δv2；

步骤3：将理论速度索引k′B按实际速度索引变换关系换算成模糊速度索引kB；

步骤4：根据模糊速度索引kB搜索B波的二维回波矩阵中lB对应的目标速度维频谱向量KB∈K×1，判断kB所在位置是否为峰值点，若不是，则跳回步骤1；

步骤5：若kB所在位置是峰值点，峰值幅度为PB，判断PA和PB差值是否小于门限值Th1。若差值小于门限值，则记录此时的速度解算索引Ci、模糊速度索引kB、峰值幅度PB，否则跳回步骤1；

步骤6：所有速度解算索引Ci换算结束后，在所有记录的Ci、kB、PB中选取最大PB对应的速度解算索引Ci作为目标速度的实际解算索引，根据式(11)计算出目标的实际非模糊速度v。

跨距离单元现象：考虑到在汽车高速运动时，在同一帧重复周期内目标距离可能存在跨距离单元的现象[8]，这会导致目标对应A波的距离维索引与B波不一致，即lA≠lB，根据lA提取出的lB对应的目标速度维频谱向量KB∈K×1出现偏差，这种偏差可以通过最大速度解算范围±V对lB进行小范围修正，修正范围公式如下：

(12)

式中，ΔlB为lB在lA基础上的修正范围，相应的修正后速度维频谱矩阵KB∈K×(2ΔlB+1)，要注意的是当ΔlB<1时不需要修正。

通过小范围扩大速度维搜索范围可以避免因跨距离单元而引起的目标失配。在汽车雷达系统中，合理选择系统参数一般可避免出现跨距离单元现象。

由于A波和B波的发射波形参数基本一致，同一目标对A波和B波的回波信号在速度维频谱呈现出的谱峰幅值和形状基本一致，选取合适的门限值Th1就可以实现目标在A波和B波的速度维频谱峰值的有效配对，进而实现正确的速度解算，且计算复杂度为o(n)，适用于汽车雷达系统工程实践。信号处理流程及具体算法流程如图3、图4所示。

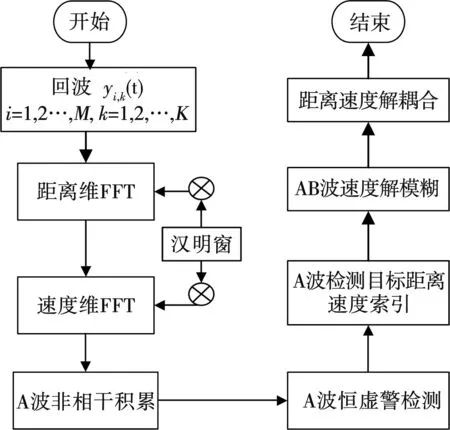
图3 信号处理流程图

图4 算法流程图

3 实测结果分析

3.1 系统参数

为了验证AB波速度解模糊算法及定位算法的有效性，采用一发四收的天线阵列，并以发射天线T为坐标原点，对远场运动目标进行距离速度参数估计。系统参数如表1所示。

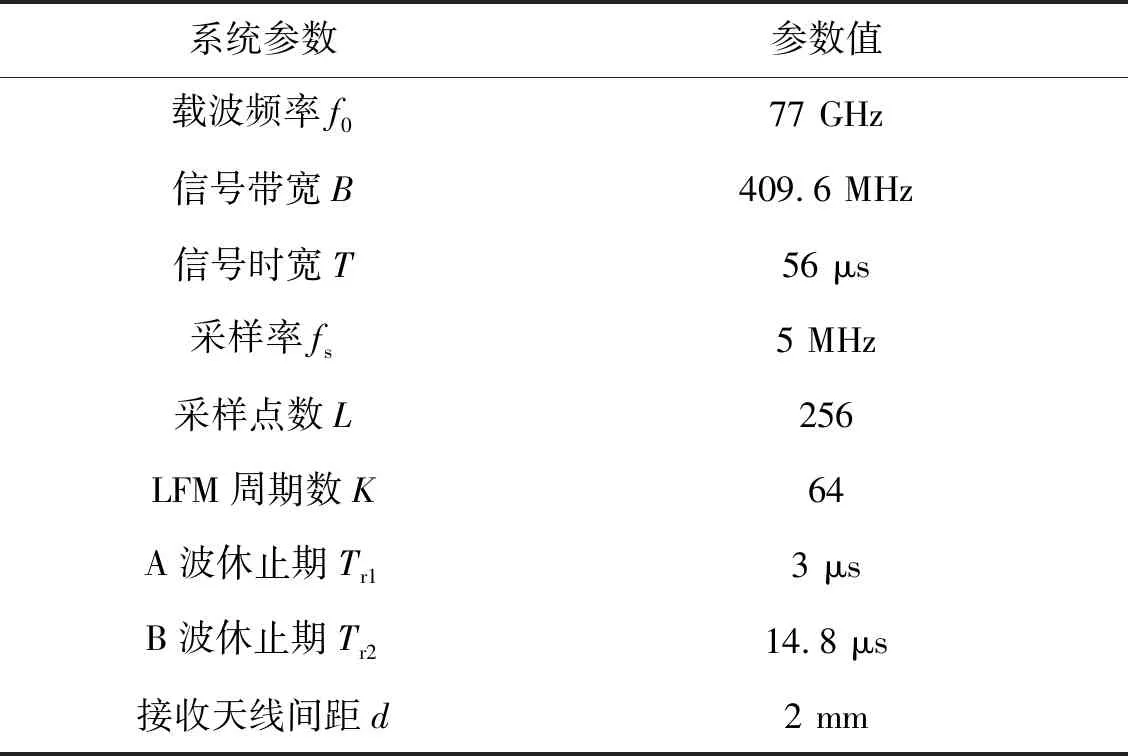
表1 系统参数

基于表1中的参数，由式(10)可以计算出系统的理论距离速度指标如表2所示。

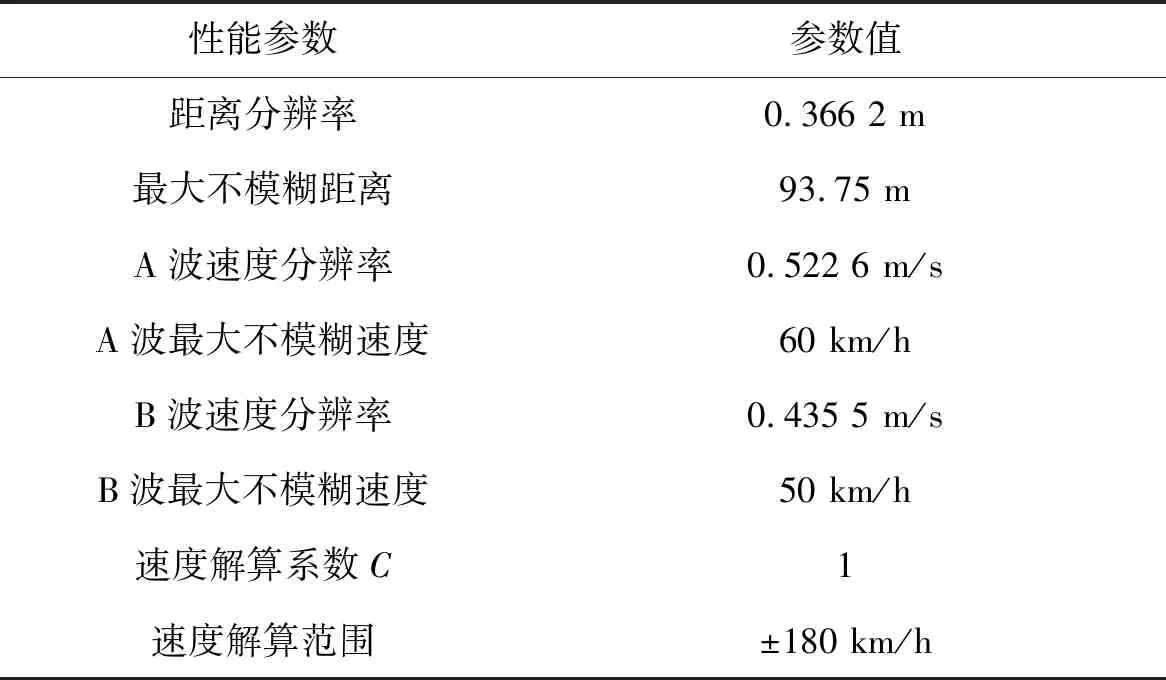
表2 性能参数

由于A波的测速范围为±60 km/h，B波的测速范围为±50 km/h，速度最大解算系数为C=2。最小盲速点为两者的最小公倍数±300 km/h。基于最大速度解算范围，根据式(12)可以计算出ΔlB=1，修正速度维频谱检测向量范围为左右各1个距离单元。

通过雷达目标模拟器和实际道路测试数据采集，针对多种特殊场景，本文对AB波速度解模糊方法进行了有效性验证。

3.2 雷达模拟器场景验证

3.2.1 同距离不同速度情况

雷达目标模拟器设置目标参数：目标1距离为60 m，速度为-130 km/h；目标2距离为60 m，速度为-150 km/h。雷达实时接收和处理模拟器模拟的目标回波，同时实时采集多帧实测数据。在MATLAB中进行离线分析，结果如图5所示。

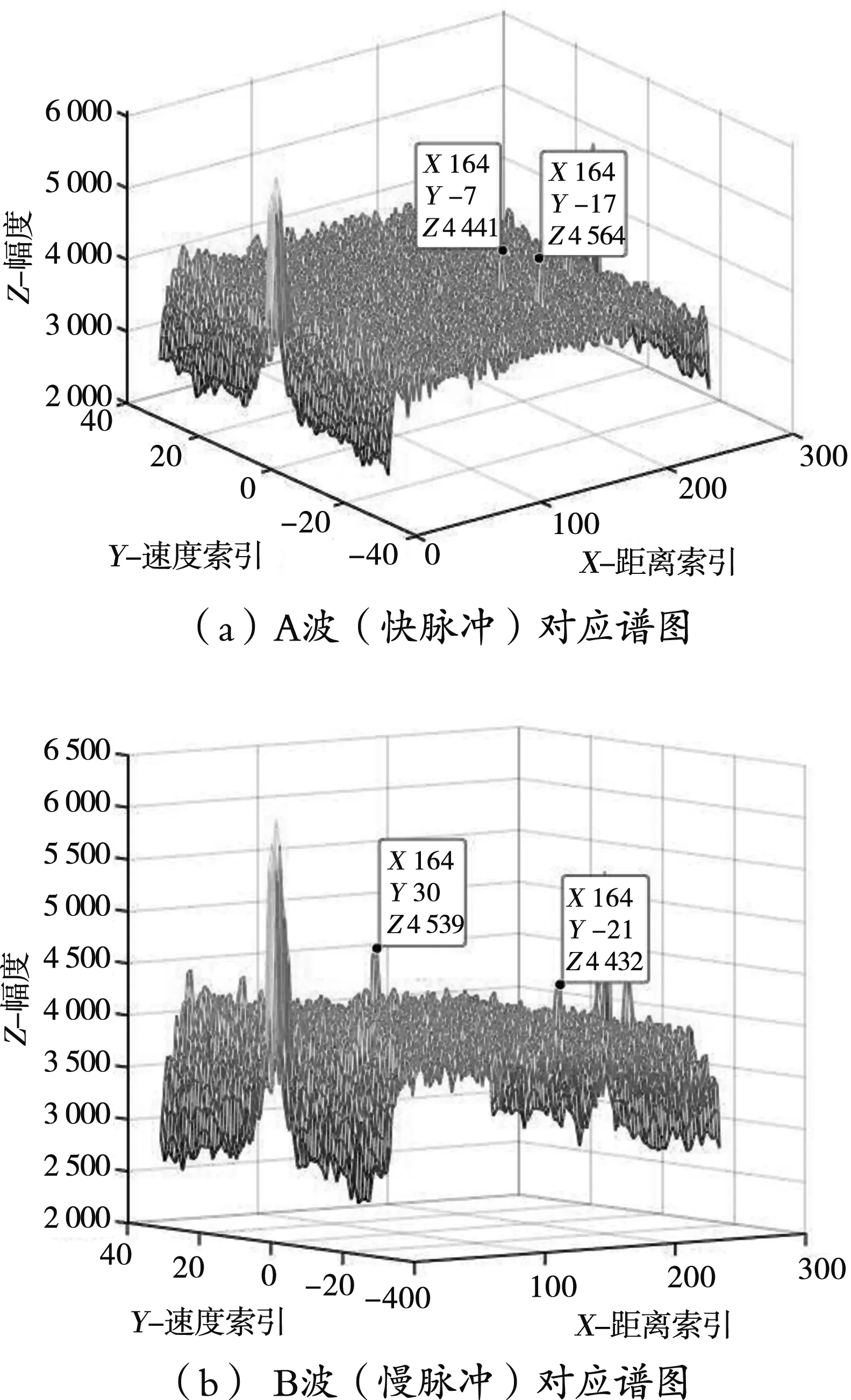
图5 同距离不同速度时的二维频谱

图5给出了双目标同距离不同速度时对应AB波的二维频谱，图5(a)对应A波，即快脉冲，可以看出两个目标的索引值分别为(164,-7,4 441)和(164,-17,4 564)。图5(b)对应B波，即慢脉冲，可以看出两个目标的索引值分别为(164,-21,4 432)和(164,30,4 539)。经过速度解模糊计算，两个目标的Ci均为-1，换算出目标距离速度分别(60.05 m，-131.7 km/h)和(60.05 m，-152.1 km/h)，忽略量化误差，与目标实际参数一致，实现了目标距离速度解耦合，验证了速度解模糊方法的有效性。

3.2.2 同速度不同距离情况

雷达目标模拟器设置目标参数：目标1距离60 m，速度-130 km/h；目标2距离50 m，速度-130 km/h。在MATLAB中离线处理对应数据， 结果如图6所示。

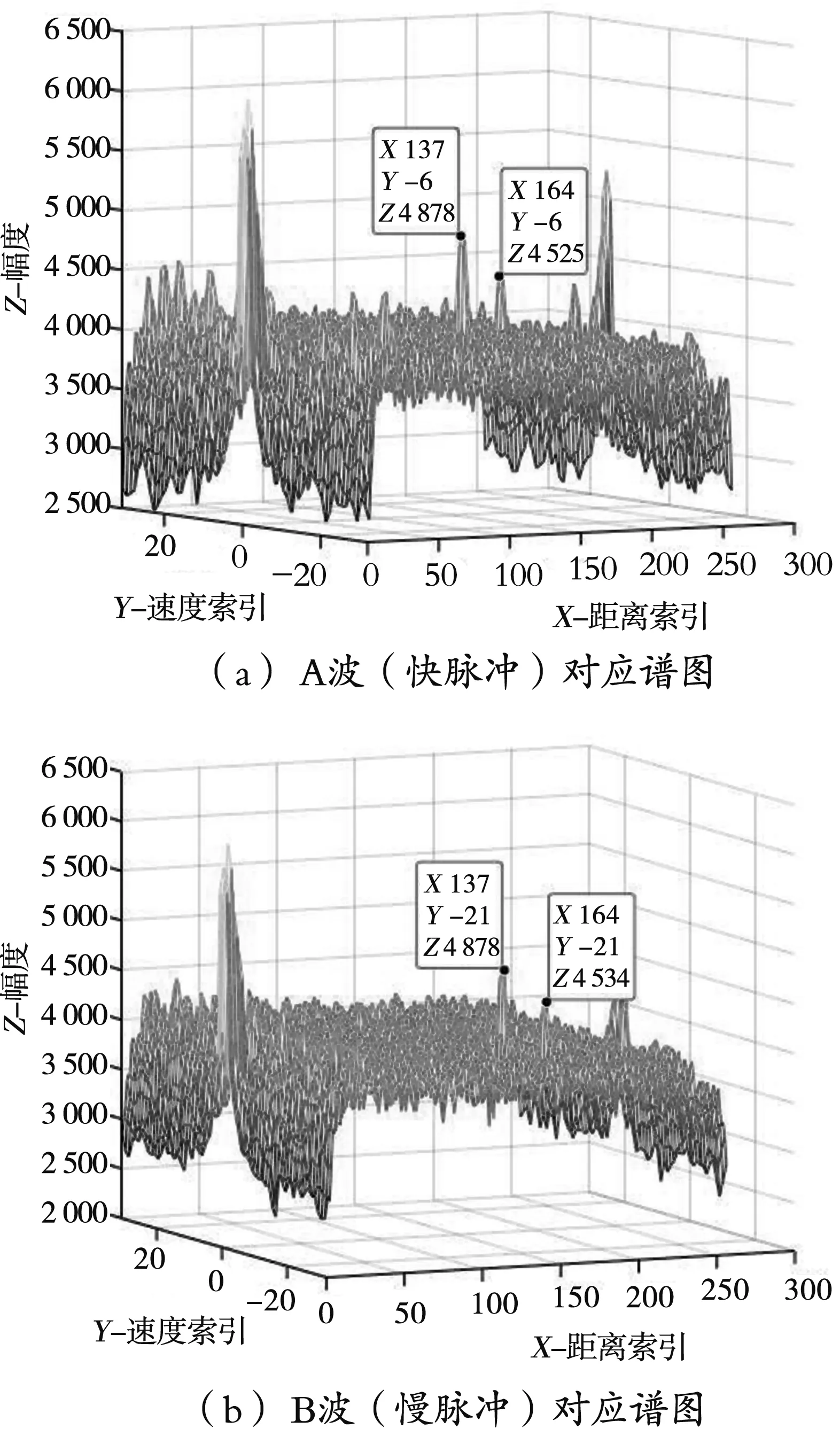
图6 同速度不同距离时的二维频谱

图6(a)对应A波，可以看出两个目标的索引值分别为(137,-6,4 878)和(164,-6,4 525)。图6(b)对应B波，可以看出两个目标的索引值分别为(137,-21,4 878)和(164,-21,4 534)。经过速度解模糊计算，双目标的Ci均为-1，换算出目标距离速度分别(50.2 m，-131.7 km/h)和(60.05 m，-131.7 km/h)，忽略量化误差，与目标实际参数一致，验证了速度解模糊方法的有效性。

3.3 道路测试场景验证

为了在实际车辆行驶环境中验证速度解模糊方法的有效性，将雷达安装在车辆正前方，在实际道路上保持静止，目标车辆位于雷达正前方驶离本车，车速由0 km/h逐渐加速到116 km/h左右，实际测试结果如图7所示。图7(a)左图显示道路测试时雷达在汽车上的安装位置，右图为目标车辆行驶过程的场景；图7(b)为雷达交互界面显示的实时探测目标信息，可以看出目标车辆在加速过程中距离本车越来越远，速度从109.08 km/h逐渐加速到116.28 km/h，与实际测试场景中目标车辆的运动过程基本一致，距离速度解算正确，验证了该方法在工程实践应用中的有效性。

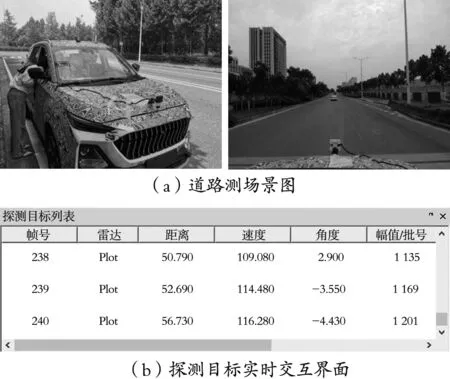
图7 道路测试验证场景和界面输出结果

4 结束语

本文研究了汽车雷达实际工程应用中高速运动目标速度解模糊和距离速度解耦合的问题。为了得到更好的距离速度估计性能，设计了一组特殊的变周期组合波形，根据参差重频解速度模糊，提出了一种最大探测速度范围便捷可变的工程实施方法。该方法对高速运动目标实现了准确的速度估计，并补偿了由多普勒频移引起的距离偏移，提高了测距精度和测速范围，在多目标情况下实现了不同目标在同距离不同速度和同速度不同距离两种特殊情况下的模糊速度解算，其有效性也通过雷达模拟器实测数据结果和道路测试结果得到了验证，对工程实践有较强的指导意义。