基于正态分布的GCr15轴承钢强化研磨残余应力场数值模拟
2022-03-31范立维梁忠伟刘晓初吴俊吴子轩耿晨谢鑫成
范立维,梁忠伟,刘晓初,吴俊,吴子轩,耿晨,谢鑫成
表面强化技术
基于正态分布的GCr15轴承钢强化研磨残余应力场数值模拟
范立维a,b,c,梁忠伟a,b,c,刘晓初a,b,c,吴俊a,b,c,吴子轩a,b,c,耿晨a,b,c,谢鑫成a,b,c
(广州大学 a.机械与电气工程学院 b.广州市金属材料强化研磨高性能加工重点实验室 c.广东省强化研磨高性能微纳加工工程技术研究中心,广州 510006)
探索强化研磨不同工艺参数下定点喷射对GCr15轴承钢残余应力场的影响规律。采用图像处理技术分析了不同工艺参数下强化研磨定点喷射表面覆盖率的分布特征。采用二维正态分布函数描述强化研磨定点喷射下钢珠的分布特征,运用Python/Opencv确定了在不同工艺参数下有限元模型所需的钢珠数量,基于Abaqus/Python构建出强化研磨正态分布有限元模型。运用所建立的正态分布模型分析不同喷射速度、钢珠直径及覆盖率对残余应力场的影响。当喷射速度从45 m/s增加到70 m/s时,表面残余压应力从‒683.5 MPa增加到‒902.4 MPa,最大残余压应力从‒981.6 MPa增加到‒1330.6 MPa,残余压力层厚度从89 µm增加到151 µm,最大残余压应力深度从30 µm移动到70 µm。当钢珠直径从0.4 mm增加到1.0 mm时,表面残余压应力先增大后减小,最大残余压应力从‒1063.5 MPa增加到‒1240.7 MPa,最大残余压应力深度从30 µm增加到60 µm,残余压应力层厚度从103 µm增加到147 µm,其中钢珠直径从0.8 mm增加到1.0 mm,最大残余压应力保持不变。当喷射覆盖率从100%到300%时,表面残余压应力、最大残余压应力及最大残余压应力深度略有增加,残余压应力层厚度几乎保持不变。将正态分布模型、随机分布模型仿真值与实验值进行比较,发现三者的表面残余压应力、最大残余压应力深度及残余压应力厚度几乎一致,最大残余压应力随机分布模型的仿真值比实验值高32.1%,正态分布模型的仿真值比实验值高18.9%。强化研磨正态分布有限元模型能够较为准确地预测残余应力变化过程,能够为强化研磨工艺参数优化提供一定的指导。
强化研磨;残余应力场;正态分布;数值模拟;GCr15轴承钢
强化研磨是一种金属材料精密加工技术,其加工原理为连续不断的钢珠、研磨粉和研磨液混合组成的研磨料在高压气体的驱动下对材料表面进行撞击,从而使材料表面形成有利于抗疲劳、抗腐蚀、抗磨损的表面类织构层(油囊、纹理)[1-2]。在强化研磨过程中,由于钢珠的高速冲击产生强化作用,会使材料表面引入残余压应力,残余压应力对裂纹扩展起抑制作用,能显著提高材料的表面性能。在课题组的前期研究中,通过实验方法探索了不同工艺参数下工件的残余应力分布[3],但在强化研磨残余应力场数值模拟方面鲜有学者进行研究,目前缺少一种能可靠预测强化研磨残余应力场的有限元模型,导致强化研磨实验加工之后仍要进行大量实验,这严重制约了强化研磨技术的研究效率。因此,建立一种可靠的强化研磨残余应力场的数值模拟模型至关重要。
近年来,贺占蜀等[4]、李雁淮等[5]建立了单丸粒和双丸粒喷丸模型,研究了不同喷丸参数对残余应力场的影响。董星等[6]、王永军等[7]、MAJZOOBI等[8]、HAN K等[9]分别建立了周向等距覆盖、阵列覆盖、对称覆盖、多层覆盖等多种多弹丸规律覆盖喷丸模型,分别采用不同简化方法模拟了喷丸动态碰撞过程,为喷丸有限元模型探索提供了多种思路。何嘉禧等[10]、LIN Qin-jie等[11]建立了喷丸三维随机覆盖仿真模型,探究了不同喷丸工艺参数对其表面完整性的影响。AHMAD等[12]、洪滔等[13]运用离散元的方法对弹丸碰撞过程建立了FEM-DEM耦合仿真模型,研究了不同覆盖率对其残余应力场的影响。然而,在实验中,为避免喷嘴堵塞,会使喷嘴隔靶材一段距离,因此强化研磨定点喷射表面覆盖率的分布并不是随机均匀分布的,而是越靠近中心区域覆盖率越高。众多研究人员通常定点喷射一定时间后,取靶材受喷中心覆盖率达到98%及以上区域作为样品,再测量样品的残余应力等实验值。在实际中,通常也有需要进行定点喷射的零件。在定点喷射过程中,测试区除了本区域内钢珠会对此区域产生碰撞强化,测试区之外的钢珠与靶材碰撞产生应力波的传递和碰撞变形,也会对观测区的残余应力场、晶粒尺寸、位错密度等强化效果评价指标值产生影响。以上研究中,单丸粒、多丸粒碰撞模型均不能体现强化研磨加工碰撞中钢珠在空间分布的随机性,而三维随机碰撞模型、FEM-DEM耦合仿真模型只研究了钢珠在空间上的随机分布,不能体现强化研磨定点喷射表面覆盖率逐渐递减的随机分布。
此外,众多学者研究了喷丸表面覆盖率对强化效果各评价指标的影响。研究结果表明,随表面覆盖率的增加,其残余应力场各特征参数、位错密度等喷丸强化效果评价指标值均缓慢增大[14-15]。但是,当表面覆盖率增加到一定程度时会使材料表面循环软化,部分位错缠结消失,残余应力更容易松驰,从而降低喷丸强化效果[16-17]。可以看出,强化研磨工艺的强化效果和效率与表面覆盖率是否合理有很大关系,而强化研磨定点喷射试验过程中表面覆盖率从喷射中心逐渐递减,各区域表面覆盖率分布不一致,当多点强化研磨时会使表面覆盖率的均匀程度难以控制,容易造成某些区域表面覆盖率过高或者过低,从而影响工件的抗疲劳性能。
综上所述,目前国内外学者为研究喷丸动态碰撞过程探索了多种有限元仿真模型,且取得了相应的研究成果,但尚未见到体现强化研磨定点喷射表面覆盖率逐渐递减的钢珠随机分布的数值仿真模型。本文采用渐进式研究方法,首先研究强化研磨定点喷射表面覆盖率的分布特征,进而建立一种新的符合强化研磨定点喷射表面覆盖率逐渐递减分布的随机碰撞仿真模型,利用新的仿真模型探究不同强化研磨工艺参数对工件残余应力场变化规律的影响,最后通过实验验证仿真模型的合理性。旨在探索一种新的强化研磨定点喷射残余应力场数值模拟方法,更准确地预测定点喷射中残余应力场随不同强化研磨工艺参数的变化过程,以提高强化研磨加工技术的研究效率。
1 强化研磨定点喷射表面覆盖率的分布特征
为了建立强化研磨钢珠的随机分布模型,首先需获取强化研磨定点喷射靶材表面覆盖率的分布特征。实验设备为广东省强化研磨高性能微纳加工工程技术研究中心自主研制的强化研磨机(如图1所示),实验材料为100 mm×75 mm×10 mm热处理后的GCr15轴承钢板,GCr15轴承钢板的硬度为55HRC。钢珠在高压气体的驱动下经文丘里管喷嘴以一定速度撞击靶材表面,在撞击区域内,凹坑密度从撞击区域中心逐渐递减,且撞击区域呈圆形。强化研磨工艺参数为:文丘里管管口直径8 mm,喷嘴到受喷靶材表面的距离80 mm,钢珠直径0.8 mm,喷射角度90°,喷射压力0.5 MPa,喷射流量2.4 kg/min,加工时间8 s。经强化研磨加工后,对样品表面进行二值化处理,如图2a所示。参照文献[18]的单次喷丸表面覆盖率分布特征的确定方法,在靶材的圆形受喷表面选取4个区域,分别记为Ⅰ、Ⅱ、Ⅲ和Ⅳ,每个区域内有若干个采样点,如图2b所示,其中区域Ⅰ的采样点直径为6 mm,其他区域采样点的直径均为3 mm。

图1 强化研磨加工设备
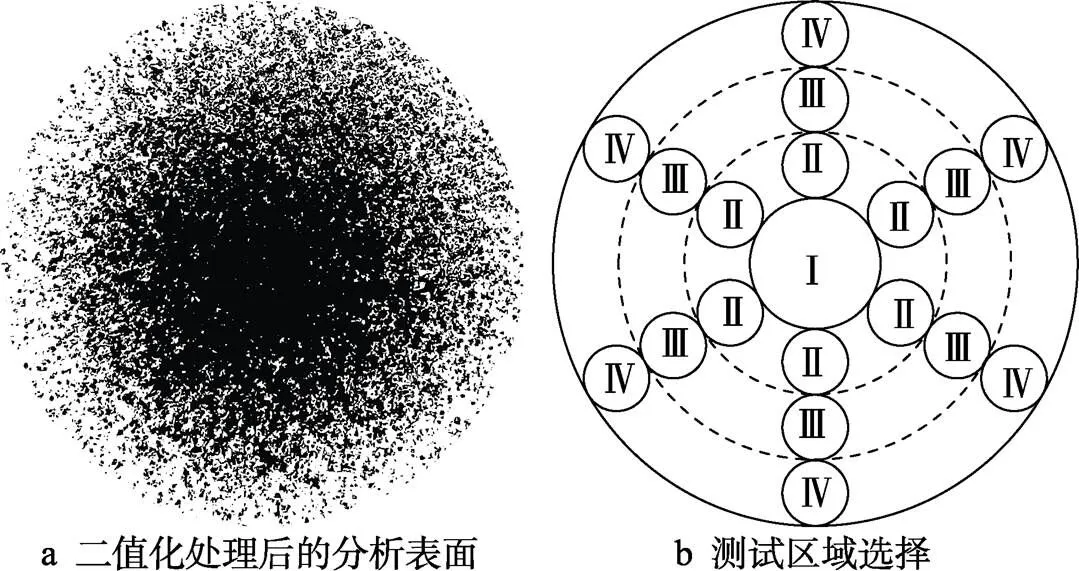
图2 沿宽度方向上强化研磨定点喷射表面覆盖率的测试方法
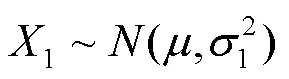
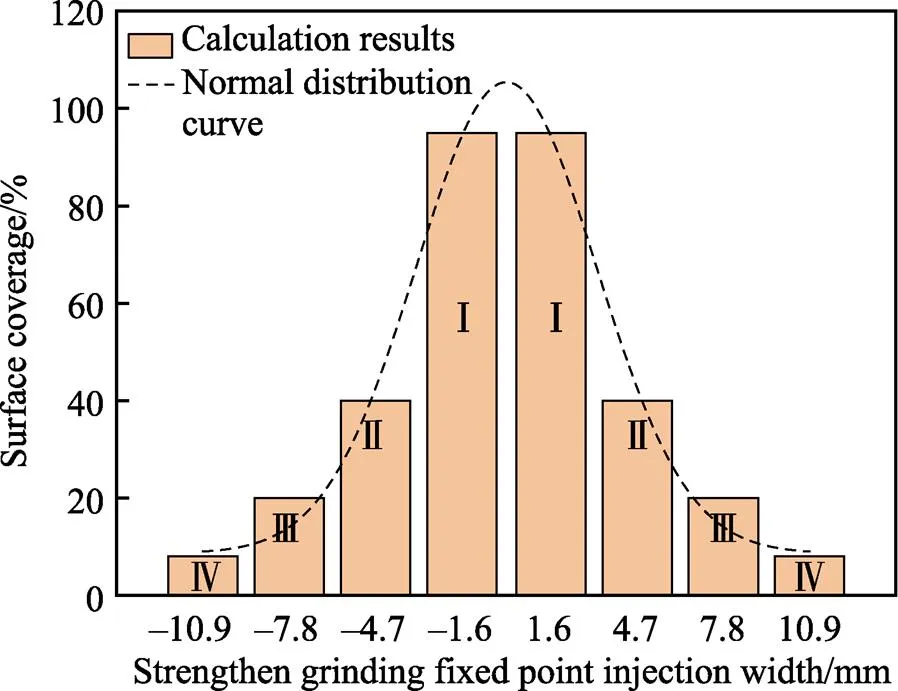
图3 强化研磨定点喷射表面覆盖率沿宽度方向上的分布规律
一维表面上覆盖率正态分布概率密度函数为:

保持其他强化研磨加工参数不变,利用上述表面覆盖率确定方法测得不同钢珠直径、不同喷射压力下强化研磨定点喷射表面覆盖率分布特征,如图4所示。其中P0.5D0.8代表压力0.5 MPa、钢珠直径0.8 mm。以下加工参数都将采用此种缩写。
2 仿真建模
强化研磨加工是一个复杂的循环动态碰撞接触过程,涉及到材料非线性、几何非线性、边界非线性等问题,建立完全符合实际情况的仿真模型极为困难。因此,为了简化仿真计算过程,在不影响研究结果的前提下,众多学者做出了如下假设[2,6]:(1)强化研磨喷射过程中起强化作用的主要是钢珠对靶材的冲击碰撞,研磨粉与研磨液的影响可忽略不计;(2)强化研磨喷射过程中所有钢球冲击靶材速度的大小和方向均相同,无速度差;(3)强化研磨喷射过程中忽略钢球间的相互作用;(4)靶面为理想光滑平面;(5)靶体为均质的各向同性材料。强化研磨定点喷射仿真模型建立过程如图5所示。

图5 强化研磨定点喷射仿真模型建立过程
2.1 几何模型
2.1.1 靶材模型
为了提高计算效率,将仿真模型等比例缩小,由于实验受喷区域呈正态分布,所以等比例缩小的仿真模型也呈对应的正态分布。基于商用有限元软件Abaqus/CAE,采用Python程序建立钢珠随机正态分布有限元模型。靶材模型尺寸为=3.5 mm、=1.5 mm的圆柱,分为观测区(区域1)、冲击区(区域2)、过渡区(区域3)、无限元区(区域4)等4个区域。观测区为残余应力场结果的提取区域,覆盖率在98%及以上。在P0.5D0.8的强化研磨喷射条件下,观测区大小为=0.43 mm、=0.6 mm。不同强化研磨加工参数下观测区的不一样,为不同加工参数的正态分布曲线下覆盖率达到98%及以上的强化研磨定点喷射宽度。冲击区为钢珠束冲击区域,即大部分钢珠的质心被限制在该区域中。过渡区为包裹着冲击区的过渡区域,可能会有极少部分钢珠分布在此区域内。最外围区域为无限元区,由于目标的几何尺寸远小于实际构件尺寸,会产生应力波反射重新进入模型而影响仿真结果的准确性,所以在最外围区域使用了无限元单元作为反射边界。图6为三维仿真模型。

图6 三维强化研磨正态分布随机碰撞模型
2.1.2 钢珠分布模型
2.1.2.1 钢珠分布函数的确定
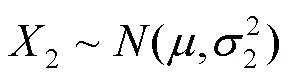

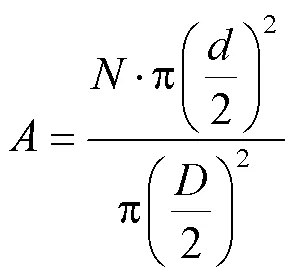
式中:为钢珠数;为单颗钢珠喷射引起的凹坑直径;为靶材料对应的冲击区域直径。
钢珠任意点(,)二维正态分布概率密度函数表示为:
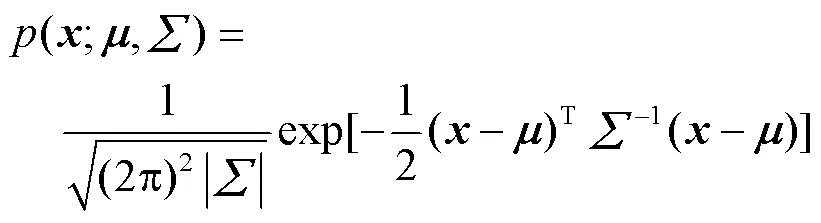
式中:=(,)t,和均为一维正态随机变量;为的期望,=(µ, µ)t;是的协方差矩阵,二维正态分布函数协方差矩阵计算公式为:
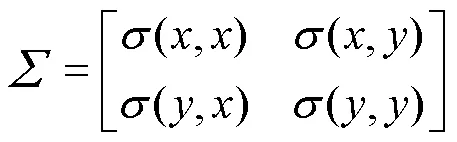
在喷射角度为90°的强化研磨定点喷射中,µ=µ==0,(,)=(,)=22=0.682,(,) =(,)=0。
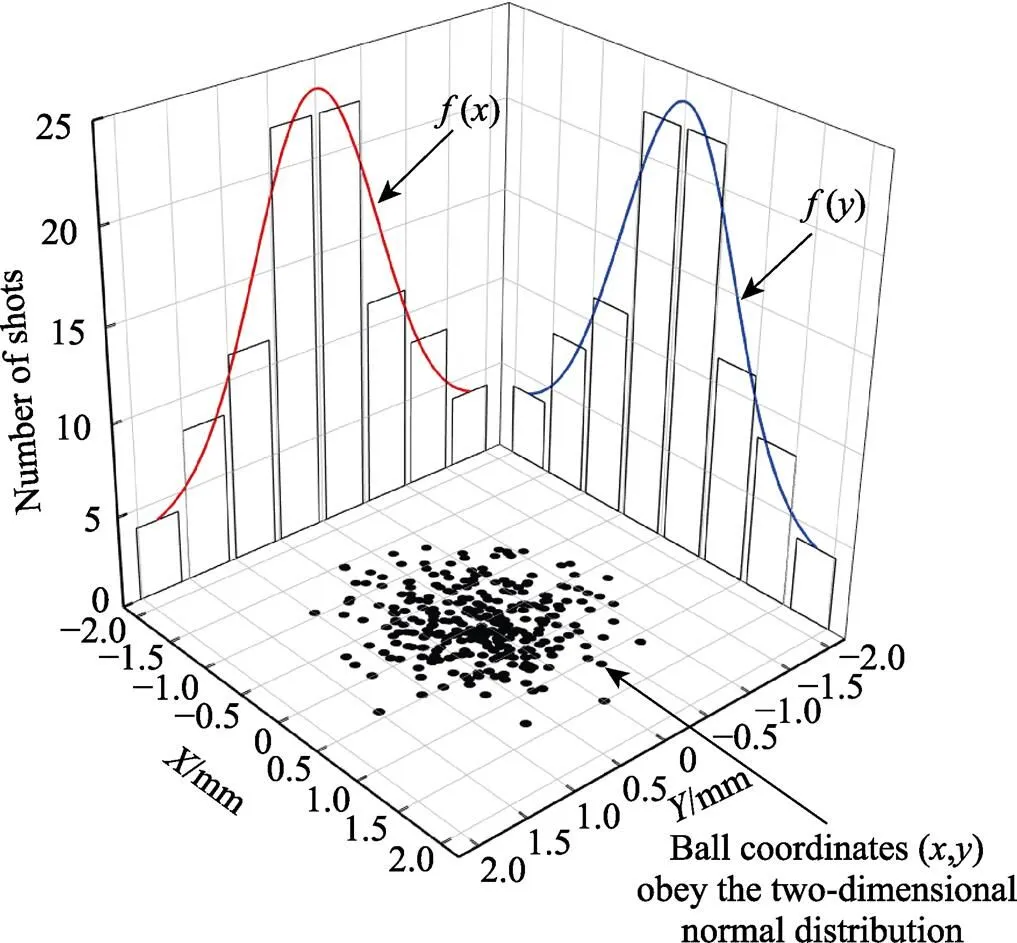
图7 钢珠坐标点(x,y)服从二维正态分布
2.1.2.2 钢珠数量及三维坐标的确定
强化研磨覆盖率是一个重要的工艺参数,它是根据强化研磨喷射后表面所有凹坑面积与表面受喷总面积的比值来计算的。在工程实践中,认为当覆盖率达到98%时,表面已被完全覆盖,只需将强化研磨时间调整为完全覆盖所需的2倍或3倍,即可获得200%或300%的覆盖率[22]。在这项研究中,假设钢珠是一个球体,并且在击中目标后,表面会形成一个半径为的规则圆形凹坑。利用Python/Opencv图像处理,如图8a所示,在圆心(0,0)半径内整个区域为红色像素点,然后遵循二维正态分布随机生成圆心为([][],[][])、半径为的黑色圆。Python程序中钢珠([][],[][])坐标二维正态分布函数如式(6)所示,每生成一个黑色圆,利用ROI提取区域内的图像信息生成图8b,计算1次半径内的Coverage值,Coverage值计算如式(7)所示。当Coverage值小于时,则在生成了个黑色圆的图像基础上继续生成第+1个黑色圆(遵循二维正态分布函数随机生成一个),然后循环上述命令去计算Coverage值,当Coverage值大于或等于(=98%)时,即退出此次循环,记录单次循环内钢珠的全部坐标([][],[][]),及整个模型所需要的钢珠总数
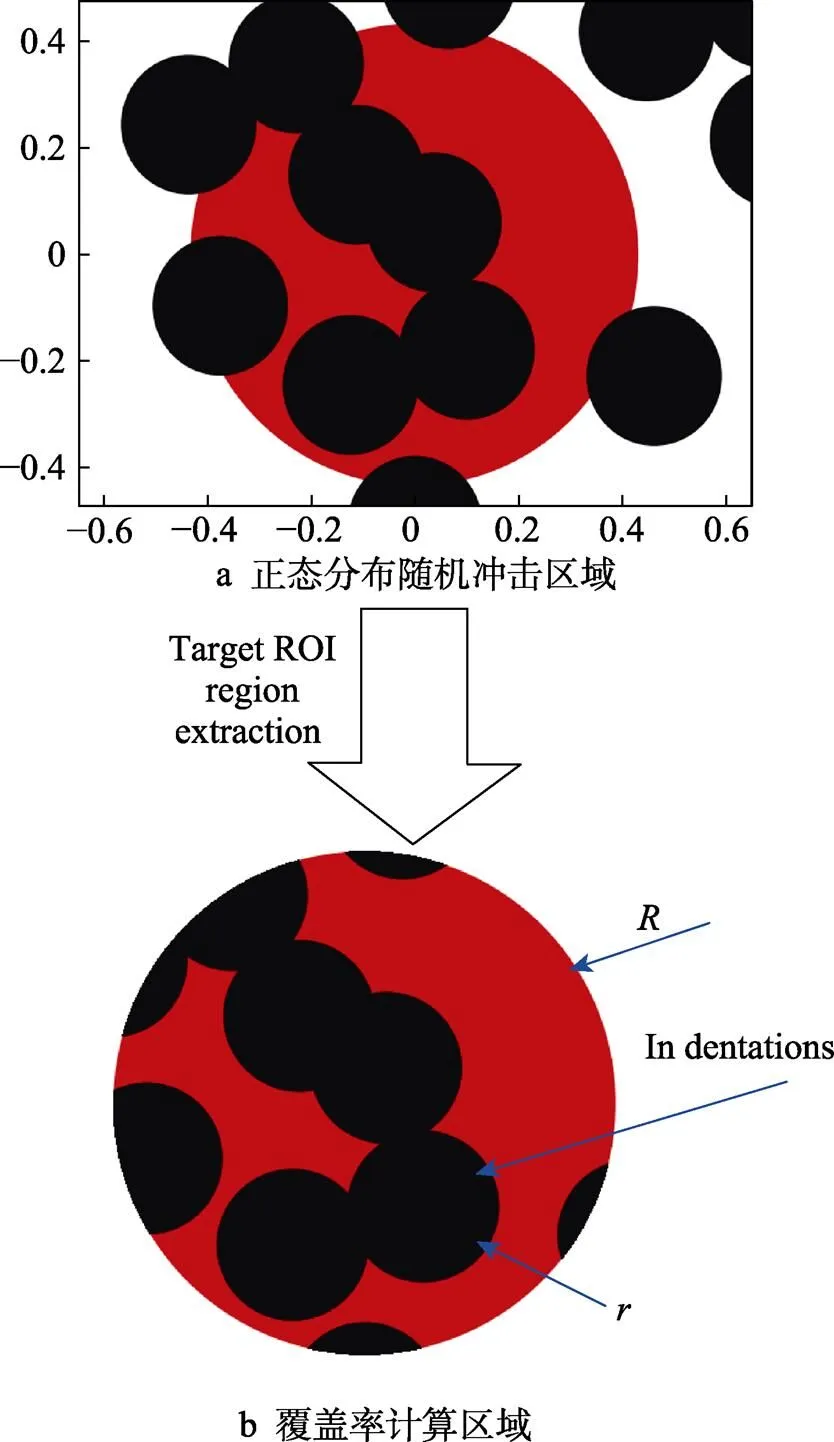
图8 强化研磨定点喷射表面覆盖率的计算方法
和影响Coverage值的钢珠数,钢珠数量确定的整个过程如图9所示。
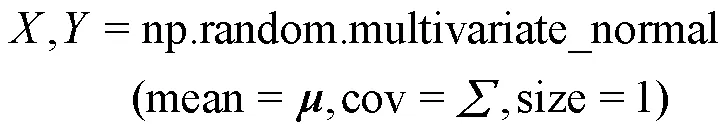
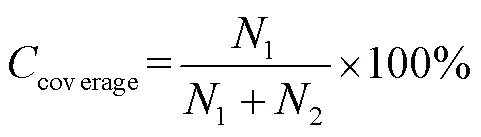
式中:np.random.multivariate_normal为python语言中的二维正态分布函数;1为黑色像素点数;2为红色像素点数。
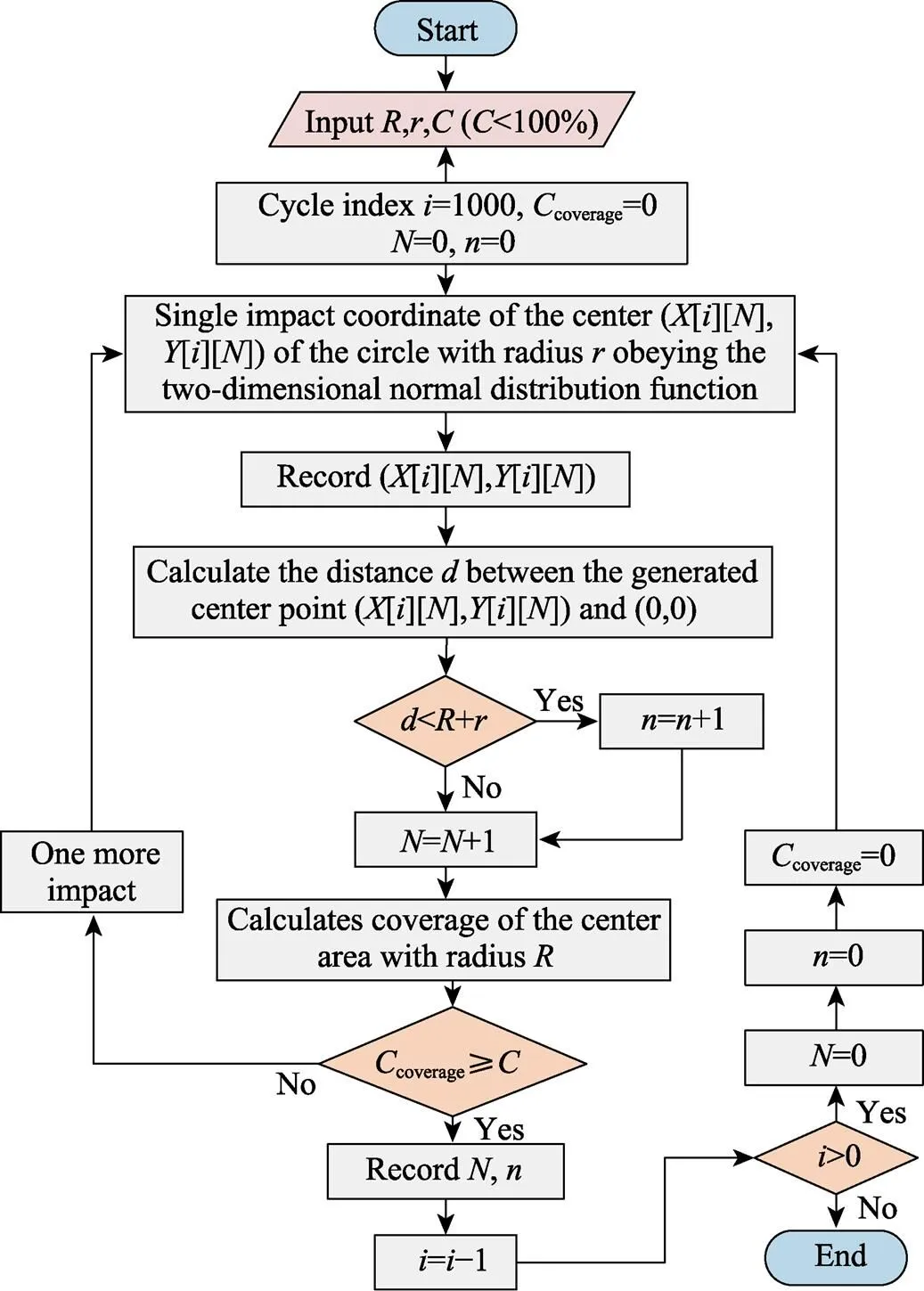
图9 钢珠数量确定流程
图10描绘了6种不同强化研磨加工参数下遵循二维正态分布在区域内覆盖率达到98%、循环1000次下所需的钢珠数的分布,发现在固定覆盖条件下所需钢珠总数量的概率分布近似呈正态分布。LIN Qin-jie等[11]在使用另外一种统计法计算随机分布下钢珠的数量时也有类似的分布特征。Avrami方程[23]是一种计算随机分布所需钢珠数量常用的经验方法,用公式(2)—(3)表示。图11将所提出的Python/ Opencv统计方法在特定区域实现全覆盖过程循环1000次的钢珠数量和的平均数、中位数与Avrami方程进行了比较,可以清楚地看到,循环1000次的钢珠数量和的平均数、中位数均近似相等;在覆盖面积为98%的区域内,python统计法记录的略高于公式法,这是因为正态分布模型越靠近中心区域,钢珠生成的概率越大,生成的概率从圆心处逐渐递减,而Avrami方程是用于随机分布的计算,每个区域生成的钢珠概率相等;其次是因为python统计法中计算的为小于+内的圆心点,所以会略高于公式法。
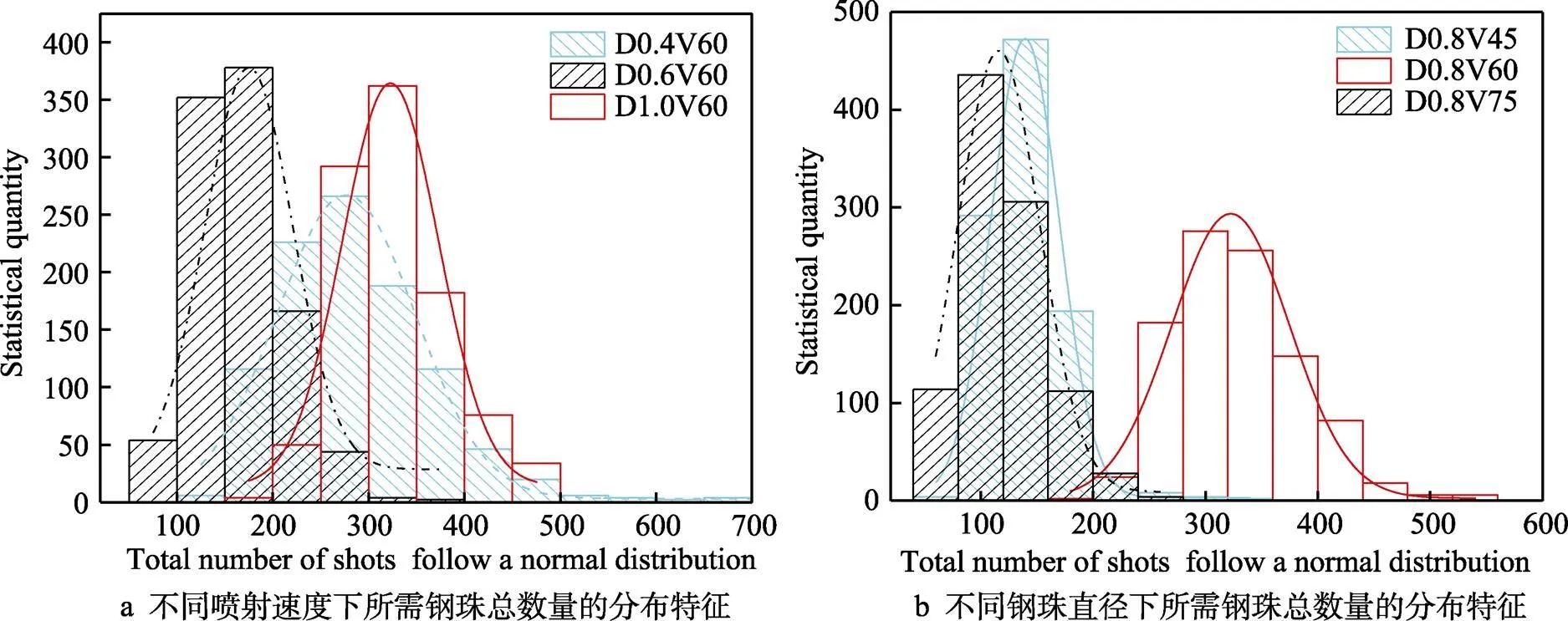
图10 循环1000次所需钢珠总数的分布特征
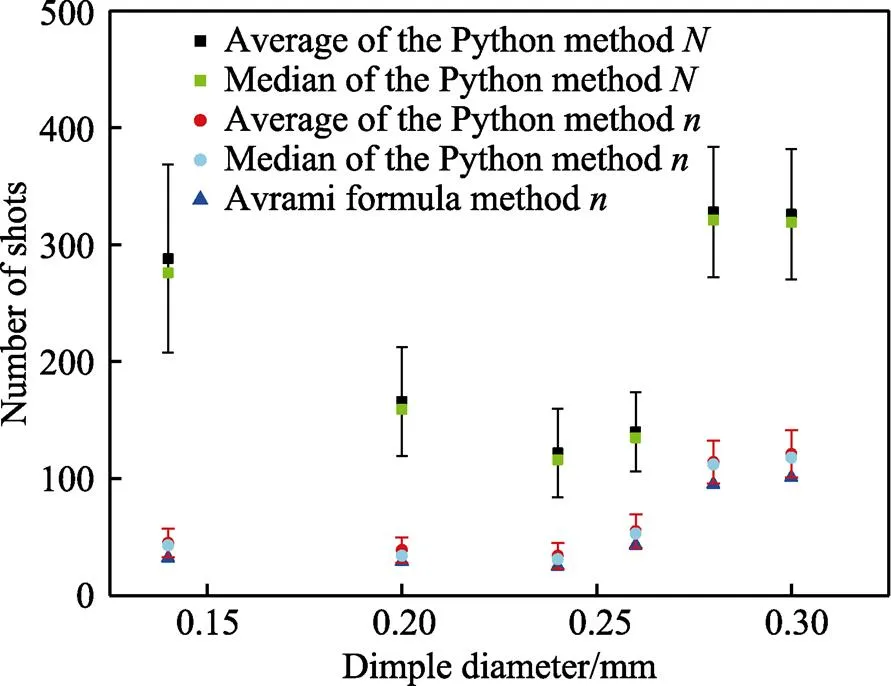
图11 统计方法与Avrami方程达到特定覆盖率所需的钢珠总数及其比较
在LIN Qin-jie等[11]针对随机分布的钢珠数量的研究中,取循环1000次所需钢珠数量的平均数作为仿真模型的钢珠数量,何嘉禧等[10]利用Avrami方程计算的钢珠数量作为仿真模型所需的钢珠数量,然后在仿真模型中利用随机函数生成钢球。但是从他们的研究结果及本文钢珠数量的Python统计方法可知,达到特定覆盖率所需的钢珠数量并不固定,而是呈正态分布。如果将循环1000次的钢珠数量平均数或者Avrami方程计算的钢珠数量作为仿真模型所需要的钢珠数量,在模型中利用随机函数或者正态分布函数生成钢珠,所生成的钢珠不一定能达到特定覆盖率,且每次仿真模型生成的钢珠数量达到的覆盖率都不一样,会存在仿真误差。为消除仿真误差,本文取循环1000次去掉最高值,即循环999次的钢珠总数量的中位数作为Abaqus模拟计算的钢珠数。在Python/Opencv运行结果中找到此次钢珠数量下记录的钢珠的全部坐标([][],[][]),然后导入Abaqus中,方向遵循随机分布,如式(8)所示,且2个钢珠之间的距离>2,基于Abaqus/Python建立了新的强化研磨随机正态分布冲击有限元模型。根据 Klemenz[24]的经验公式(9),可以建立实验参数与仿真参数的关系。
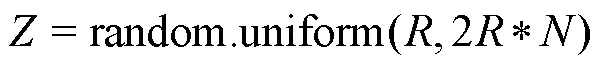

式中:random.uniform为Python语言中的随机函数;为钢珠的平均速度,m/s;为喷射压力,MPa;为钢珠的直径,mm;为钢球的进给流量,kg/min。
本次强化研磨实验中,=2.4 kg/min。在D0.8P0.3、D0.8P0.5、D0.8P0.7强化研磨加工参数下,对应的仿真参数分别约为D0.8V45、D0.8V60、D0.8V75,单颗钢珠造成的凹坑直径分别为0.24、0.26、0.28 mm。在D0.4P0.5、D0.6P0.5、D1.0P0.5强化研磨加工参数下,对应的平均速度均约为60 m/s,对应的凹坑直径分别为0.14、0.2、0.3 mm。
2.2 材料模型
强化研磨加工过程中,钢珠高速撞击靶材表面,靶材受冲击表面会在极短时间内发生剧烈的塑性变形,在剧烈的塑性变形中材料发生应变硬化、应变率强化和温度软化效应,而在Johnson-cook材料动态本构模型均有体现,能够很好地用来描述材料在高应变率条件下应力-应变的关系[25],因此在强化研磨仿真模型中应用该材料本构模型,其具体表达式为:

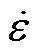
表1 GCr15轴承钢J-C本构模型参数

Tab.1 J-C constitutive model parameters of GCr15 bearing steel
2.3 网格划分与边界条件
网格划分上,在本模型中,钢珠采用四节点线性四面体单元C3D4,靶材无限元区的网格为无限单元CIN3D8,靶材其余区域为八节点线性六面体减缩积分单元C3D8R,且进行沙漏控制;对观测区×内进行局部网格细化,网格最小尺寸为0.03 mm×0.03 mm× 0.01 mm;对靶材底面自由度进行完全约束。钢珠与靶材表面的相对切向运动使用库伦摩擦模型描述,定义库伦摩擦因数为0.25[27]。钢珠与靶材的接触为面-面接触,力学约束公式化为罚接触方法。
3 结果与分析
3.1 喷射速度对残余应力分布的影响
强化研磨之后,零件表层区域的残余应力场对材料表面性能的改善十分重要。因为强化研磨主要是通过钢珠对零件表面的冲击来强化,所以强化研磨残余应力场的表征方式通常参考喷丸的描述方式,以表面残余压应力、最大残余压应力、最大残余压应力深度和残余压应力层厚度这4个特征参数的变化来描述残余应力场的分布特征[3]。残余压应力对裂纹扩展起抑制作用,能够明显地改善材料的表面性能。
在残余压力的测量过程中,对强化研磨后的试样表面利用电腐蚀剥层处理。然后利用X射线衍射法测量不同深度的残余应力值,通常X射线的测量光斑直径为1 mm,测量得到的残余应力值为同深度上X射线测量光斑范围内的应力平均值。所以,在有限元仿真中,为了准确地描述残余应力场在每个深度上的结果,利用Python程序提取观测区在该深度水平上每层节点的平均应力值,从而得到沿深度方向残余应力的分布曲线。
图12显示了利用建立的随机正态分布仿真模型在=0.8 mm、=100%时不同喷射速度下残余应力的分布。结果表明,随着喷射速度从45 m/s增加到75 m/s,残余压力层厚度从89 µm增加到151 µm。这表明强化研磨喷射速度的增加可以获得更厚的残余压应力层;同时,随着喷射速度的增加,最大残余压应力出现在较深的位置,从30 µm移动到70 µm;最大残余压应力深度和残余应力层厚度的增加是由于喷射速度的增加,使钢珠携带的动能增大,钢珠冲击材料表面,从而使材料表层塑性变形渗透层的深度增加[28]。另外,当喷射速度从45 m/s增大到75 m/s时,表面残余压应力从‒683.5 MPa增加到‒902.4 MPa,最大残余压应力从‒981.6 MPa增加到‒1330.6 MPa。这是由于钢珠动能的增加使材料表层塑性变形程度增大,从而造成了表面残余压应力和最大残余压应力增加。从图12中可以观察到,喷射速度从60 m/s增大到75 m/s时,表面残余压应力和最大残余压应力的增加幅度较低。这是因为GCr15轴承钢为高强度钢,屈服强度比较高,不容易发生塑性变形,其值随着速度的增加容易达到饱和状态,这与钟轶宁等人[28]的研究结果一致。另外有研究表明,表面残余压应力值和次表层的最大残余压应力值的最主要影响因素是材料的力学性能,而不是喷射强度[29]。
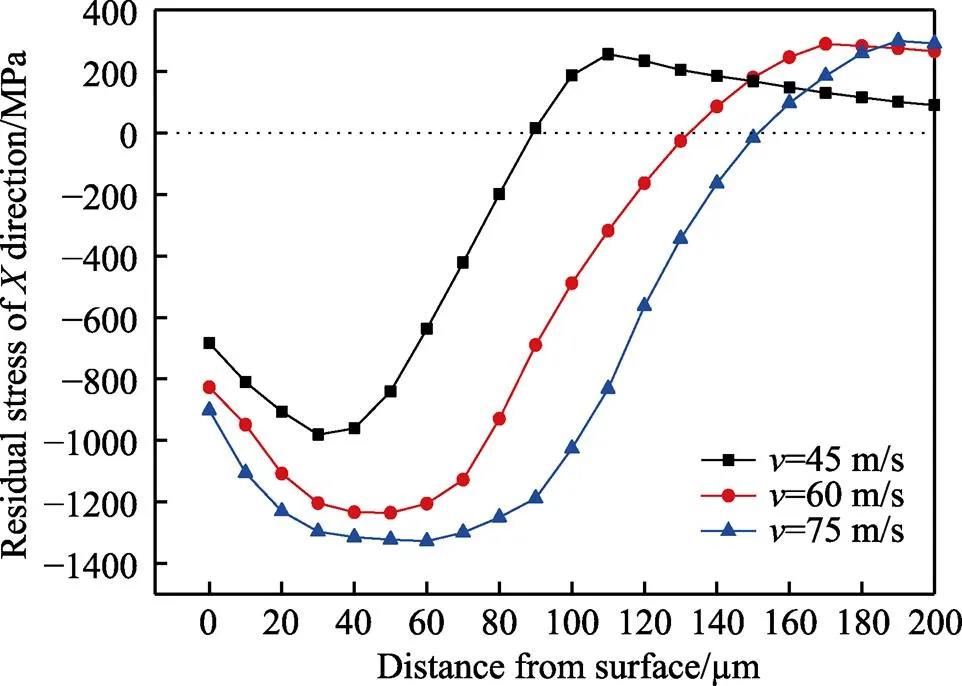
图12 不同喷射速度下残余应力沿深度方向上的分布情况
3.2 钢珠直径对残余应力的影响
图13描述了在=60 m/s、=100%时不同钢珠直径下残余应力的变化。从图13中可以观察到,当钢珠直径从0.4 mm增加到1.0 mm时,最大残余压应力从‒1063.5 MPa增加到‒1240.7 MPa,最大残余压应力深度从30 µm增加到60 µm,残余压应力层厚度从103 µm增加到147 µm。这是因为,由钢珠直径与冲击能量的关系式[30]可知,钢珠的动能与钢珠直径的立方成正比,当钢珠直径增大时,钢珠携带的动能显著增大,靶材表面因为受到钢珠冲击造成塑性变形的程度增大及塑性变形渗透层的影响深度显著增大;其次,根据赫兹接触理论可知,最大剪切应力出现在次表层[31],因此导致次表层的残余压应力增大明显。值得注意的是,从图13中可以观察到,钢珠直径从0.8 mm增加到1.0 mm时,表面残余压应力反而减小,最大残余压应力几乎不变。这是因为在单位面积内总能量相差不是很大的情况下,钢珠直径越大,则与靶材表面的接触面积越大,会造成最表层区域塑性变形程度相对较小,次表面塑性变形总体程度几乎不变,但又因为随直径的增大,单颗钢珠携带的动能增大,所以塑性变形渗透层的影响深度增大,从而表现为钢珠直径太大表面残余压应力反而降低,次表层残余压应力高,最大残余压应力深度向基体内移动。在张广良[32]、ZHANG等[33]的研究中也表明,在总能量大致相同的情况下,钢珠直径越小,表面塑性变形程度越高,表面残余压应力越大。
针对上述的研究结果,众多学者研究了二次喷丸技术,即一次喷丸通过大尺寸钢珠喷射,之后第二次喷丸采用小尺寸钢珠喷射,这样可以提高喷丸效果[10-11],进一步提高材料的表面性能[34-35]。
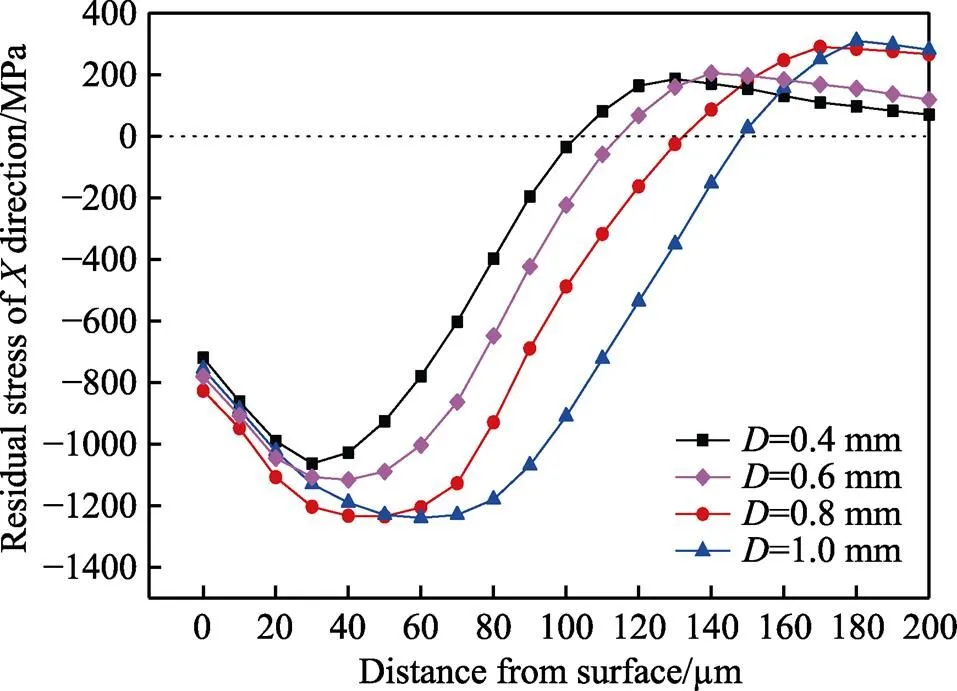
图13 不同钢珠直径下残余应力沿深度方向上的分布情况
3.3 覆盖率对残余应力的影响
图14描述了在=0.8 mm、=60 m/s时不同覆盖率下残余应力场的变化。从图14中可以观察到,当覆盖率从100%增加到300%时,表面残余压应力的增量很小,仅从‒827 MPa增加到‒898 MPa。这说明表面覆盖率的增加对表面残余压应力的影响不大,这与LIN等[11]的研究结果一致。当覆盖率从100%增加到200%时,最大残余压应力从‒1236.4 MPa增加到‒1305.6 MPa,最大残余压应力深度略有增加,在60~110 µm深度范围内,残余压应力均增幅较大,这可能是因为相邻区域覆盖率增加,使得相邻区域内的残余拉应力区域逐渐消失并且转化为残余压应力,所形成的残余压应力层的影响深度与全覆盖观测区域的残余压应力层的影响深度逐渐重叠;其次是因为随着覆盖率的增加,材料表面循环硬化程度增强,用于塑性变形的能量减少,动能转化为材料内部弹性能增多,赫兹压力效应更加显著[36],使得最大残余压应力往内移动和残余压应力增大。当覆盖率从200%增加至300%时,材料残余压应力的增加量很小,逐渐趋向于稳定,这是因为在此喷射速度下残余应力场逐渐饱和所致。同时,随着覆盖率从100%增加到300%,残余压力层厚度保持不变。这是因为覆盖率的增加并没有改变单颗钢球的动能,钢珠动能转化为影响应力波渗透层深度的能量不变,没有足够的能量去影响更深层区域的残余应力的分布。因此,覆盖率的增加不能改变残余压应力层厚度,这与WU Ji-zhan等[37]的发现相符。
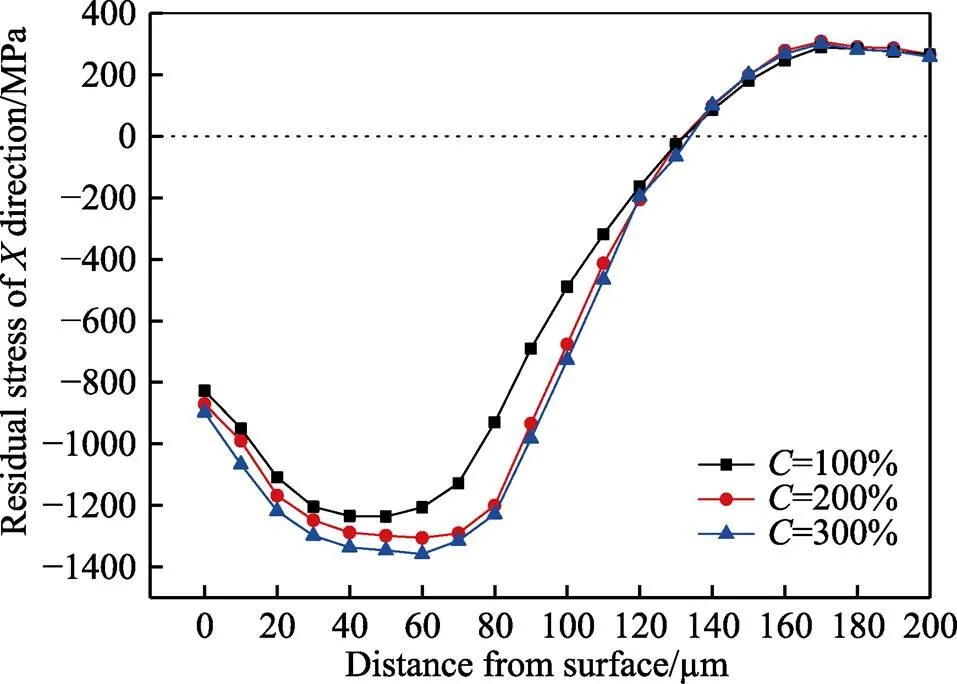
图14 不同强化研磨覆盖率下残余应力沿深度方向上的分布情况
4 实验验证
为了验证正态分布仿真模型的合理性,将随机分布模型、正态分布模型的残余应力模拟结果与实验结果进行对比。通过强化研磨机对GCr15轴承钢进行强化研磨处理,喷射压力为0.5 MPa,钢珠直径为0.8 mm,加工时间为8 s,其他加工参数见第1节,然后取覆盖率达到98%及以上的试样中心区域进行残余应力检测实验的制样。残余应力采用Proto I XRD射线应力分析仪检测。采用Cr靶Kα辐射,管电流为5 mA,管电压为25 kV。通过控制电解腐蚀时间对试样进行剥层处理,以获取试样在不同深度下的残余应力值。
图15为强化研磨后GCr15轴承钢的残余应力仿真与实验结果。由图15可知,正态分布模型、随机分布模型与实验结果,在残余应力曲线的形状与趋势方面基本一致,三者表面残余压应力、最大残余压应力深度和残余压应力层厚度基本一致,残余应力层厚度为120~140 µm,最大残余压应力深度为40~50 µm,但正态分布模型与随机分布模型的结果值都略高于实验值。这可能是因为,在仿真模型中,为了计算效率通常会把钢珠约束为刚体,而实验中由于GCr15轴承钢属于高强度钢,即使钢珠与GCr15轴承钢靶体有一定的硬度差,但在高速冲击下钢珠还是会发生塑性变形,钢珠的塑性变形会消耗自身大量的动能,所以会造成仿真模拟中靶体的塑性变形程度大于实验中强化研磨试样的塑性变形程度,从而使仿真模型残余压应力值偏大。WU Gang等[38]研究了多弹丸仿真模型下不同钢珠硬度对残余应力分布的影响,发现不同硬度和约束为刚体状态下的钢珠对靶材冲击时,残余应力的分布曲线相差较大。在仿真模拟中,钢珠是以确定的速度和垂直的角度冲击靶材,而喷射式强化研磨实验中使用文丘里管喷嘴且距离待加工工件有一定的距离,会使实验中钢珠的喷射速度和喷射角度具有一定的随机性,这2种误差的共同作用下,造成实验值偏小。

图15 强化研磨后GCr15轴承钢残余应力仿真值与实验值
另外,正态分布模型仿真值的最大残余压应力为‒1236.4 MPa,实验值最大残余压应力为‒1040 MPa,模拟误差为18.9%,随机分布模型仿真值的最大残余压应力为‒1374.3 MPa,模拟误差为32.1%。可见,正态分布模型仿真值与实验结果更加接近,而随机分布模型与实验结果的误差较大。这可能是因为,如图16所示不同仿真模型下轴平面的残余应力分布云图,在钢珠的高速冲击下,材料表层发生了剧烈的塑性变形,为了抵抗塑性变形,材料表层会产生残余应力,材料表面表现为一定深度的残余压应力场,同时材料内部为了达到平衡,会在更深层区域形成一个残余拉应力场;在正态分布模型中,相邻区域由于覆盖率不高(低于98%),低于98%区域,在压应力评估区域也存在残余拉应力[28,38],所形成的残余压应力层厚度会低于全覆盖观测区域的残余压应力层厚度,则在相邻区域更深层区域形成的残余拉应力场所造成的拉应力方向的波动的影响深度会和观测区所产生的残余压应力场的影响深度部分重叠,并会抵消部分残余压应力,董星等[6]、何嘉禧等[10]的仿真模型中也表明了存在此现象,所以正态分布模型的仿真值更接近实验值。
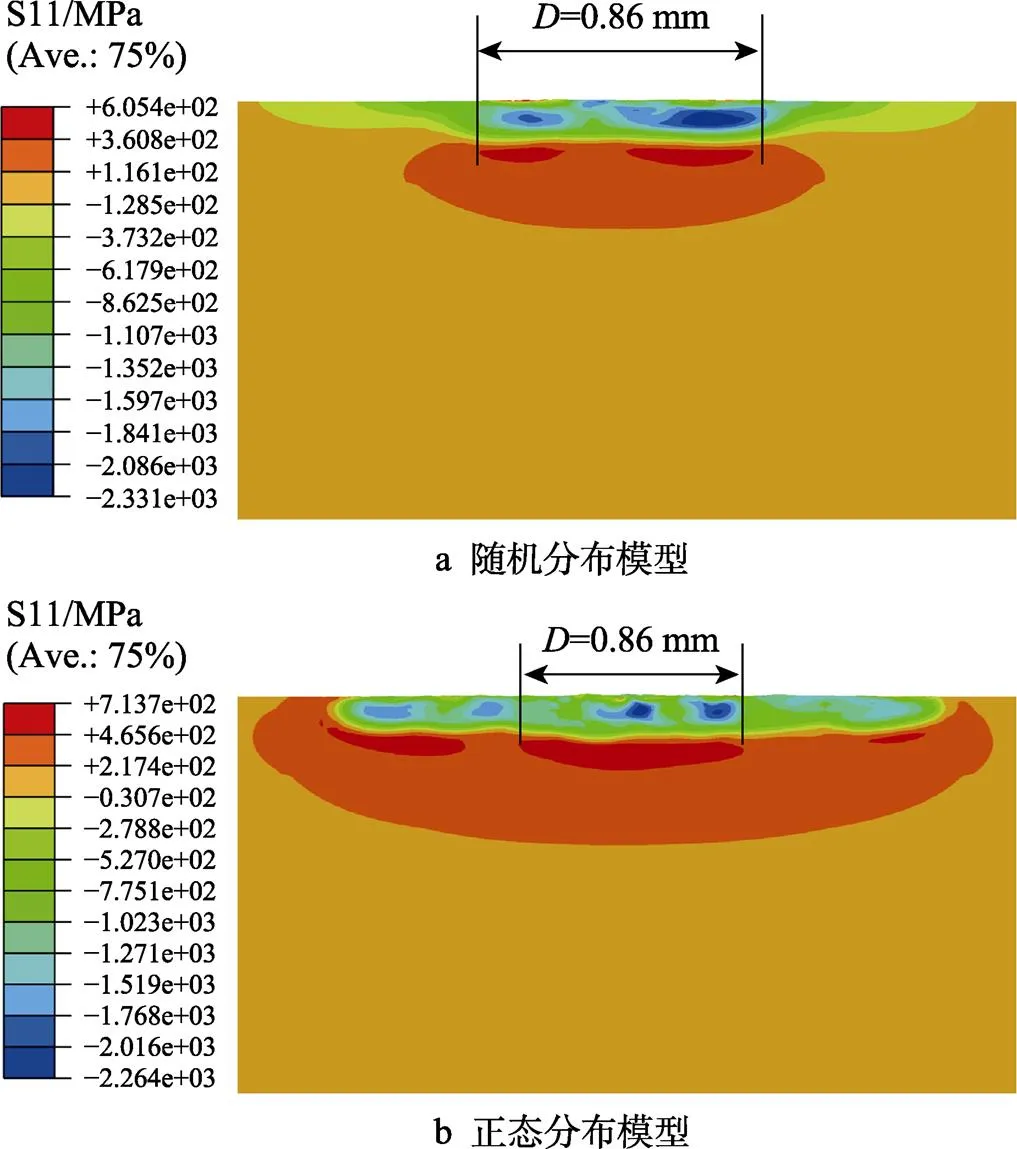
图16 不同仿真模型下轴平面残余应力分布云图
总的来说,可认为强化研磨正态分布模型在一定程度上能够较为准确地模拟强化研磨实验的残余应力变化过程,这对强化研磨工艺参数优化具有一定的指导意义。
5 结论
1)仿真结果表明,强化研磨能够使GCr15轴承钢表层产生一定厚度的残余压应力层,残余压应力在次表面达到最大值,同时会在更深层区域产生残余拉应力层,以使材料内部达到平衡。
2)随着强化研磨喷射速度的增加,表面残余压应力、最大残余压应力深度及残余压应力层厚度均有明显提高。随着钢珠直径的增大,表面残余压应力先增大再减小,但能够显著提高最大残余压应力、最大残余压应力深度及残余压应力层厚度。覆盖率的增加对残余应力的分布影响最小。
3)强化研磨正态分布模型残余应力的仿真结果与实验结果有较好的一致性,能够对强化研磨工艺参数优化提供一定的指导。
[1] LIANG Zhong-wei, LIU Xiao-chu, XIAO Jin-rui, et al. Adaptive Prediction of Abrasive Impacting Pressure Effectiveness in Strengthen Jet Grinding Using NSAE- ANFIS[J]. The International Journal of Advanced Manufacturing Technology, 2020, 106(7-8): 2805-2828.
[2] 刘晓初, 刘镇, 梁忠伟, 等. 基于随机碰撞的GCr15钢强化研磨表面粗糙度数值模拟[J]. 表面技术, 2021, 50(4): 385-392.
[3] LIU Xiao-chu, LIU Zhen, LIANG Zhong-wei, et al. Numerical Simulation of Surface Roughness of GCr15 Steel Strengthened Grinding Based on Random Impact[J]. Surface Technology, 2021, 50(4): 385-392.
[4] 黎达成. 强化研磨中喷射压力对轴承钢残余应力场的影响[D]. 广州: 广州大学, 2019.
[5] LI Da-cheng. Influence of Injection Pressure on Residual Stress Field of Bearing Steel in Strengthen Grinding[D]. Guangzhou: Guangzhou University, 2019.
[6] 贺占蜀, 陈雷, 李超, 等. 单丸粒和双丸粒喷丸模型的有限元模拟[J]. 塑性工程学报, 2020, 27(4): 153-158.
[7] HE Zhan-shu, CHEN Lei, LI Chao, et al. Finite Element Simulation of Single and Double Shot Peening Model[J]. Journal of Plasticity Engineering, 2020, 27(4): 153-158.
[8] 李雁淮, 王飞, 吕坚, 等. 单丸粒喷丸模型和多丸粒喷丸模型的有限元模拟[J]. 西安交通大学学报, 2007, 41(3): 348-352.
[9] LI Yan-huai, WANG Fei, Lyu Jian, et al. Finite Element Analysis for Shot-Peening Models of Single Shot Impact and Multiple Impingement[J]. Journal of Xi'an Jiaotong University, 2007, 41(3): 348-352.
[10] 董星, 刘雨庆, 段雄. 前混合水射流多弹丸喷丸模型及残余应力场的数值模拟[J]. 机械工程学报, 2020, 56(4): 224-232.
[11] DONG Xing, LIU Yu-qing, DUAN Xiong. Numerical Simulation of Multi-Shot Shot Peening Models and Residual Stress Field of Premixed Water Jet[J]. Journal of Mechanical Engineering, 2020, 56(4): 224-232.
[12] 王永军, 孙宝龙, 张炜, 等. 铝锂合金喷丸强化数值模拟及试验[J]. 航空动力学报, 2015, 30(3): 595-602.
[13] WANG Yong-jun, SUN Bao-long, ZHANG Wei, et al. Numerical Simulation and Experiment on Shot Peening of Al-Li Alloy[J]. Journal of Aerospace Power, 2015, 30(3): 595-602.
[14] MAJZOOBI G H, AZIZI R, NIA A A. A Three-Dimensional Simulation of Shot Peening Process Using Multiple Shot Impacts[J]. Journal of Materials Processing Technology, 2005, 164-165: 1226-1234.
[15] HAN K, OWEN D R J, PERIC D. Combined Finite/ Discrete Element and Explicit/Implicit Simulations of Peen Forming Process[J]. Engineering Computations, 2002, 19(1): 92-118.
[16] 何嘉禧, 汪舟, 甘进, 等. 二次喷丸42CrMo钢表面完整性的数值模拟研究[J]. 表面技术, 2020, 49(6): 216-223.
[17] HE Jia-xi, WANG Zhou, GAN Jin, et al. Numerical Simulation on Surface Integrity of 42CrMo Steel after Dual Shot Peening[J]. Surface Technology, 2020, 49(6): 216- 223.
[18] LIN Qin-jie, LIU Huai-ju, ZHU Cai-chao, et al. Effects of Different Shot Peening Parameters on Residual Stress, Surface Roughness and Cell Size[J]. Surface and Coatings Technology, 2020, 398: 126054.
[19] AHMAD A S, WU Yun-xin, GONG Hai. Coupled Finite and Discrete Element Shot Peening Simulation Based on Johnson-Cook Material Model[J]. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2020, 234(7): 974- 987.
[20] 洪滔, 王志伟, 袁巨龙. 喷丸强化过程的有限元和离散元模拟[J]. 中国机械工程, 2008, 19(11): 1321-1325.
[21] HONG Tao, WANG Zhi-wei, YUAN Ju-long. Numerical Simulation of Shot Peening Process Using Finite Element and Discrete Element Method[J]. China Mechanical Engineering, 2008, 19(11): 1321-1325.
[22] WU Ji-zhan, LIU Huai-ju, WEI Pei-tang, et al. Effect of Shot Peening Coverage on Residual Stress and Surface Roughness of 18CrNiMo7-6 Steel[J]. International Journal of Mechanical Sciences, 2020, 183: 105785.
[23] GHASEMI A, HASSANI-GANGARAJ S M, MAHMOUDI A H, et al. Shot Peening Coverage Effect on Residual Stress Profile by FE Random Impact Analysis[J]. Surface Engineering, 2016, 32(11): 861-870.
[24] 王欣, 蔡建明, 王强, 等. 喷丸表面覆盖率对Ti60高温钛合金疲劳性能的影响[J]. 中国表面工程, 2011, 24(5): 58-63, 103.
[25] WANG Xin, CAI Jian-ming, WANG Qiang, et al. Effect of Shot Peening Surface Coverage on the Fatigue Property in Ti60 High-Temperature Titanium Alloy[J]. China Surface Engineering, 2011, 24(5): 58-63, 103.
[26] 李瑞鸿, 刘道新, 张炜, 等. 喷丸强化与表面完整性对300M钢疲劳性能的影响[J]. 机械科学与技术, 2011, 30(9): 1418-1423.
[27] Li Rui-hong, Liu Dao-xin, Zhang Wei, et al. Influence of Shot Peening and Surface Integrity on the Fatigue Properties of 300M Steel[J]. Mechanical Science and Technology, 2011, 30(9): 1418-1423.
[28] 盛湘飞, 李智, 周楠楠, 等. 基于正态分布的喷丸表面覆盖均匀程度与强化效率研究[J]. 表面技术, 2018, 47(5): 227-232.
[29] SHENG Xiang-fei, LI Zhi, ZHOU Nan-nan, et al. Uniformity of Surface Coverage and Strengthening Efficiency in Shot Peening Process Based on Normal Distribution[J]. Surface Technology, 2018, 47(5): 227-232.
[30] 谢鑫成. 基于强化研磨加工的工业机器人轴承内圈滚道表面覆盖率的研究[D]. 广州: 广州大学, 2020.
[31] XIE Xin-cheng. Study on Raceway Surface Coverage of Industrial Robot Bearing Inner Ring Based on Strengthen Grinding Processing[D]. Guangzhou: Guangzhou University, 2020.
[32] 吴文海, 蓝天, 张霆, 等. 喷丸过程中喷嘴移速对颗粒分布的影响[J]. 表面技术, 2020, 49(8): 342-349.
[33] WU Wen-hai, LAN Tian, ZHANG Ting, et al. Effect of Nozzle Moving Speed on Particle Distribution during Shot Peening[J]. Surface Technology, 2020, 49(8): 342- 349.
[34] OHTA T, INOUE A. Measurement and Functional Approximation of Peening Intensity Distributions[J]. Materials Transactions, 2019, 60(6): 1004-1010.
[35] BAGHERIFARD S, GHELICHI R, GUAGLIANO M. On the Shot Peening Surface Coverage and Its Assessment by Means of Finite Element Simulation: A Critical Review and some Original Developments[J]. Applied Surface Science, 2012, 259: 186-194.
[36] KIRK D, ABYANEH M Y. Theoretical Basis of Shot Peening Coverage Control[J]. The Shot Peener, 1993, 2(9): 28-30.
[37] KLEMENZ M. Anwendung Der Simulation Der Randschichtausbildung Beim Kugelstrahlen Auf Die Abschätzung Der Schwingfestigkeit Gekerbter Bauteile[D]. Karlsruhe: Karlsruhe University, 2009.
[38] SANJURJO P, RODRÍGUEZ C, PEÑUELAS I, et al. Influence of the Target Material Constitutive Model on the Numerical Simulation of a Shot Peening Process[J]. Surface and Coatings Technology, 2014, 258: 822-831.
[39] 张方圆. 硬切削GCr15轴承钢表面变质层微观组织及抗磨损性能研究[D]. 大连: 大连理工大学, 2019.
[40] ZHANG Fang-yuan. Study on Microstructure and Wear Resistance of the Metamorphic Layer of GCr15 Bearing Steel in Hard Cutting[D]. Dalian: Dalian University of Technology, 2019.
[41] 李源, 雷丽萍, 曾攀. 弹丸束喷丸有限元模型数值模拟及试验研究[J]. 机械工程学报, 2011, 47(22): 43-48.
[42] LI Yuan, LEI Li-ping, ZENG Pan. Shot Stream Finite Element Model for Shot Peening Numerical Simulation and Its Experiment Study[J]. Journal of Mechanical Engineering, 2011, 47(22): 43-48.
[43] 钟轶宁. 喷丸处理Ti-6Al-4V合金残余应力场特征与演变规律研究[D]. 大连: 大连理工大学, 2018.
[44] ZHONG Yi-ning. Analysis of Characteristics and Evolution of Residual Stress Field of Shot Peened Ti-6Al-4V Alloy[D]. Dalian: Dalian University of Technology, 2018.
[45] SEGURADO E, BELZUNCE F J, PARIENTE I F. Effects of Low Intensity Shot Peening Treatments Applied with Different Types of Shots on the Fatigue Performance of a High-Strength Steel[J]. Surface and Coatings Technology, 2018, 340: 25-35.
[46] JOHNSON W. Impact Strength of Materials[M]. UK: Edward Arnold Publishers LTD, 1972.
[47] JOHN K L. Contact Mechanics[M]. Cambridge: Cambridge University Press, 1985.
[48] 张广良. 不同强度钢喷丸残余应力的有限元模拟[D]. 上海: 上海交通大学, 2012.
[49] ZHANG Guang-liang. Study on Finite Element Simulation of Shot Peening of Different Yield Strength Steeland Its Residual Stress[D]. Shanghai: Shanghai Jiao Tong University, 2012.
[50] ZHANG Ya-long, LAI Fu-qiang, QU Sheng-guan, et al. Effect of Shot Peening on Residual Stress Distribution and Tribological Behaviors of 17Cr2Ni2MoVNb Steel[J]. Surface and Coatings Technology, 2020, 386: 125497.
[51] 孙寒骁, 朱有利, 侯帅, 等. 疲劳载荷对17CrNiMo6喷丸强化层残余应力与组织的影响[J]. 中国表面工程, 2016, 29(4): 43-48.
[52] SUN Han-xiao, ZHU You-li, HOU Shuai, et al. Effects of Fatigue Load on Residual Stress and Microstructure of 17CrNiMo6 Shot Peening Strengthened Layer[J]. China Surface Engineering, 2016, 29(4): 43-48.
[53] WANG Xin, LI Si-qing, YANG Qing, et al. Effect of Double Shot Peening on Room-Temperature Notched Fatigue Property of TC4 Titanium Alloy[J]. Materials Science Forum, 2015, 817: 90-95.
[54] SHERAFATNIA K, FARRAHI G H, MAHMOUDI A H. Effect of Initial Surface Treatment on Shot Peening Residual Stress Field: Analytical Approach with Experimental Verification[J]. International Journal of Mechanical Sciences, 2018, 137: 171-181.
[55] WU Ji-zhan, LIU Huai-ju, WEI Pei-tang, et al. Effect of Shot Peening Coverage on Hardness, Residual Stress and Surface Morphology of Carburized Rollers[J]. Surface and Coatings Technology, 2020, 384: 125273.
[56] WU Gang, WANG Zhou, GAN Jin, et al. FE Analysis of Shot-Peening-Induced Residual Stresses of AISI 304 Stainless Steel by Considering Mesh Density and Friction Coefficient[J]. Surface Engineering, 2019, 35(3): 242- 254.
Numerical Simulation of Residual Stress Field in Strengthened Grinding of GCr15 Bearing Steel Based on Normal Distribution
a,b,c,a,b,c,a,b,c,a,b,c,a,b,c,a,b,c,a,b,c
(a. School of Mechanical & Electric Engineering, b. Guangzhou Key Laboratory for Strengthened Grinding and High Performance Machining of Metal Material, c. Guangdong Engineering and Technology Research Centre for Strengthen Grinding and High Performance Micro-nanomachining, Guangzhou University, Guangzhou 510006, China)
This paper aims to explore the influence of fixed point injection on residual stress field of GCr15 bearing steel under different process parameters of strengthening grinding. Image processing technology was used to analyze the distribution characteristics of the surface coverage along the width direction of the strengthening grinding fixed point injection under different process parameters. The two-dimensional normal distribution function was used to describe the distribution characteristics of steel ball coordinates under the fixed point injection of strengthening grinding. Python/Opencv was used to determine the number of steel balls required by the finite element model under different process parameters. Based on Abaqus/ Python, the finite element model with normal distribution of strengthening grinding was constructed. Using the established normal distribution model, the influence of different injection velocity, ball diameter and coverage rate on the residual stress field was analyzed. When the injection velocity increased from 45 m/s to 70 m/s, the surface residual compressive stress increased from ‒683.5 MPa to ‒902.4 MPa, the maximum residual compressive stress increased from ‒981.6 MPa to ‒1330.6 MPa, and the thickness of residual pressure layer increased from 89 μm to 151 μm. The maximum residual compressive stress depth was moved from 30 μm to 70 μm. When the diameter of the steel ball increased from 0.4 mm to 1.0 mm, the surface residual compressive stress increased first and then decreased, the maximum residual compressive stress increased from ‒1063.5 MPa to ‒1240.7 MPa, and the maximum residual compressive stress depth increased from 30 μm to 60 μm. The thickness of residual compressive stress layer increased from 103 μm to 147 μm, and the diameter of steel ball increased from 0.8 mm to 1.0 mm, and the maximum residual compressive stress almost remained unchanged. When the injection coverage rate was from 100% to 300%, the surface residual compressive stress, the maximum residual compressive stress and the maximum residual compressive stress depth increased slightly, and the residual compressive stress layer thickness almost remained unchanged. The simulation values of the normal distribution model and the random distribution model were compared with the experimental values, and it was found that the surface residual compressive stress, maximum residual compressive stress depth and residual compressive stress thickness of the three models were almost the same. The simulation values of the random distribution model and the normal distribution model were 32.1% and 18.9% higher than the experimental values of the maximum residual compressive stress. The finite element model with normal distribution can accurately predict the change process of residual stress, which can provide some guidance for the optimization of process parameters of strengthening grinding.
strengthened grinding; residual stress field; normal distribution; numerical simulation; GCr15 bearing steel
2021-05-18;
2021-08-18
FAN Li-wei (1997—), Male, Postgraduate, Research focus: surface hardening technology of metal materials.
梁忠伟(1978—),男,博士,教授,主要研究方向为智能制造及装备技术。
LIANG Zhong-wei (1978—), Male, Doctor, Professor, Research focus: intelligent manufact uring and equipment technology.
范立维,梁忠伟,刘晓初,等. 基于正态分布的GCr15轴承钢强化研磨残余应力场数值模拟[J]. 表面技术, 2022, 51(3): 242-253.
Tg580.68
A
1001-3660(2022)03-0242-12
10.16490/j.cnki.issn.1001-3660.2022.03.026
2021-05-18;
2021-08-18
国家自然科学基金项目(51975136,51575116);广东省科技计划项目(2017A010102014,2016A010102022);国家重点研发计划(2018YFB2000501);广州大学全日制研究生基础创新项目资助(2020GDJC-M18);广东省高等学校科技创新团队项目(2017KCXTD025);广州市教育系统创新学术团队项目(1201610013);广东省高校重点领域专项(2019KZDZX1009);广州市科技计划项目(201707010293)
Fund:National Natural Science Foundation of China (51975136, 51575116); Guangdong Science and Technology Program Project (2017A010102014, 2016A010102022); National Key Research and Development Project (2018YFB2000501); Innovation Research for the Postgraduates of Guangzhou University under Grant (2020GDJC-M18); Guangdong Province University Science and Technology Innovation Team Project (2017KCXTD025); Guangzhou Education System Innovation Academic Team Project (1201610013); Special Projects in Key Fields of Universities in Guangdong Province (2019KZDZX1009); Guangzhou Science and Technology Program Project (201707010293)
范立维(1997—),男,硕士研究生,主要研究方向为金属材料表面强化技术。
FAN Li-wei, LIANG Zhong-wei, LIU Xiao-chu, et al. Numerical Simulation of Residual Stress Field in Strengthened Grinding of GCr15 Bearing Steel Based on Normal Distribution[J]. Surface Technology, 2022, 51(3): 242-253.
