耦合空化效应的超声滚压系统流场结构优化设计
2022-03-31郭永磊郑建新朱立新商映举邓瀚林
郭永磊,郑建新,朱立新,商映举,邓瀚林
耦合空化效应的超声滚压系统流场结构优化设计
郭永磊,郑建新,朱立新,商映举,邓瀚林
(河南理工大学 机械与动力工程学院,河南 焦作 454003)
实现耦合空化效应的超声滚压系统流场结构的优化,提升超声滚压加工质量。首先,利用Fluent流场仿真软件模拟超声滚压加工流场空化情况,获取滚珠周边3个关键位置的气含率。其次,采用最优拉丁超立方方法进行实验设计,并以流场结构参数为优化变量,以3个关键位置气含率为优化目标,基于二阶响应面法建立气含率近似模型。然后,综合运用AHP和熵权法确定各个气含率的权重值,采用遗传算法NSGA-II对近似模型进行优化求解来获取最优流场结构参数。最后,对优化结构与初始结构下获得的气含率进行对比,验证优化结果。基于20组最优拉丁超立方试验结果所构建的二阶响应面近似模型拟合度较好,3个关键位置气含率均在95%置信水平上均通过显著性检验。综合分析后,3个优化目标的权重分别为0.2791、0.2516和0.4692,获得的优化结构的3个关键位置气含率相较于初始结构分别提升了21.6%、156.4%、44.1%,效果明显。优化后的流场结构可以应用在超声滚压加工系统中以提升加工过程中的空化效应。
超声滚压;空化效应;气含率;结构优化
超声滚压加工是一种在深滚加工技术基础上引入超声频振动而形成的复合加工技术。相较于滚压加工,超声滚压加工过程中仅需要较小的静压力[1]就可以获得较好的加工效果,能消除零件的表面微观缺陷,降低表面粗糙度值,产生冷作硬化和残余压应力,并在表层形成纳米梯度结构,从而有效提高零件耐磨、耐腐蚀和抗疲劳性能[2-5]。但在超声滚压加工时常利用空气压力[6]或弹性组件[7]而非深滚时的高压流体系统[1,8]来使滚珠与工件保持紧密接触,因而无法在滚压区域产生超声空化效应。已有试验证明,加工区域的切削液在超声波正负压相的作用下,能够发生有益的空化效应[9-14]。
祝锡晶团队[10,15-16]对功率超声珩磨过程中的空化效应进行研究,发现在一定的条件下,空化效应有助于改善加工过程中工件的表面质量。他们对AZ31B镁合金分别在水和煤油中进行超声空化改性处理,发现不同介质中,材料均发生了硬度提高和晶粒尺寸下降的现象。Ding等人[17]对5052铝合金进行自激振荡脉冲水射流喷丸,结果表明,在水射流和空化效应的共同作用下,表面质量明显改善,与未处理表面相比,硬度和残余应力分别增加了61.69%和148%。Tan等人[18]对铬镍铁合金工件进行超声空化抛光处理,结果表明,工件的表面粗糙度降低高达40%。由此可见,合理利用空化效应可以对加工质量带来积极影响。
显然,若在超声滚压中也引入空化效应,则有望进一步提高强化质量。在超声滚压中,流场的引入还受限于其超声振动声学系统结构,不能影响其谐振状态,因此结构不能有较大的变动。在此限定条件下,如何设计出合适的流场结构来尽可能提高超声滚压加工过程的空化效应,提升加工质量,需要深入研究。
本文将建立超声滚压加工过程中流场空化模型,采用最优拉丁超立方实验设计方法对管道直径、倾斜段长度和锥口直径3个流场结构参数进行试验设计,选用二阶响应曲面近似模型建立优化目标与结构参数之间的近似数学模型。最后采用多目标遗传算法NSGA-II求解近似数学模型,以期得到最优的流场结构参数组合,提升超声滚压加工质量。
1 结构变量与优化目标
1.1 流场几何模型
超声滚压系统由超声波发生器、换能器、变幅杆、工具系统(包含滚珠)组成,如图1所示[19]。其中滚珠在工具头前端凹槽中可以自由滚动,通过压盖限制滚珠的位置防止脱落。凹槽中开有导液沟槽,用于切削液的流动。在滚压过程中,声学系统安装在刀架上。滚珠以进给速度r在静压力s和超声频振动作用下对以转速为的工件表面进行冲击碾压,实现表面的冲击强化和光整加工。滚珠的谐振频率=24.71 kHz,纵振振幅L=4.2 μm,扭振振幅T=1.8 μm。在滚压过程中,同时开启外接液压系统和机床供液系统,使工具头内腔及滚珠滚压区域充满切削液。
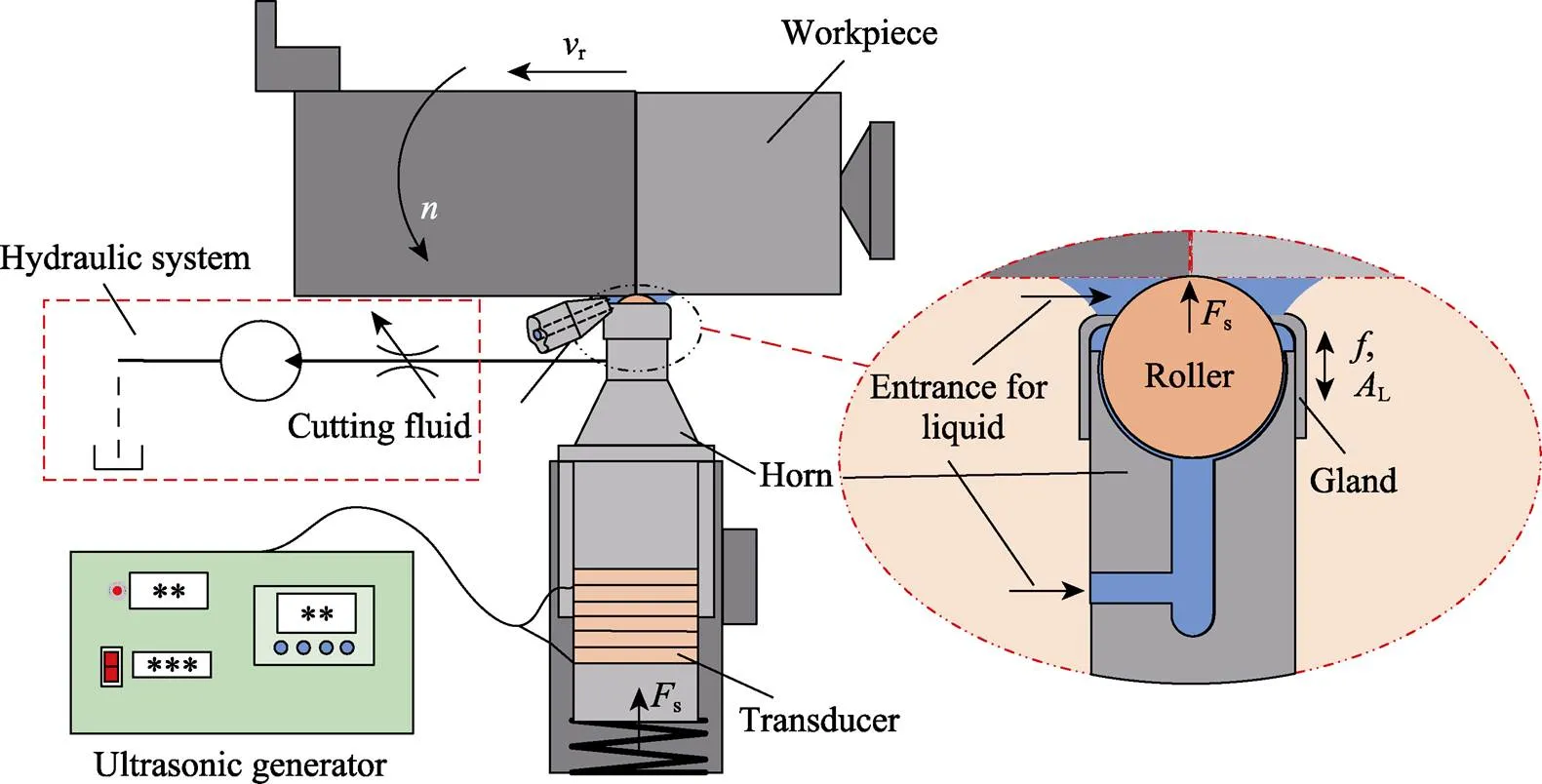
图1 超声滚压加工过程示意图
对超声滚压装置流场区域进行二维简化,忽略扭转振动对空化效应的影响,建立如图2所示超声滚压空化仿真二维模型[19]。图2中,Roller为滚珠,进行动网格设置,做超声频振动;、、、、、组成内腔壁;、、为简化腔内外交界面,通过和向腔内供液(压力入口),为压力出口;为滚压时的工件表面。加工过程中,滚珠与工件表面()在一个超声振动周期内同时存在接触和分离状态,但是在进行数值模拟过程中,滚珠与工件表面无法接触,同时考虑到网格质量与计算精度,设置两者间隔为0.1 mm。设模型内腔中心线为轴,以压力入口中心线与轴的交点作为坐标原点。

图2 空化流场仿真模型
1.2 流场结构参数
为避免过大影响系统谐振频率及超声信号的传递,滚珠周边结构不宜改变。借鉴Laval喷管渐扩段和渐缩段结构设计,通过改变段形状来进行流场结构设计,如图2所示。选取直管段管道直径、倾斜段长度和锥口高度作为结构参数。考虑实际工具系统的可加工性和结构参数的变动范围不能影响超声滚压声学系统谐振频率,设定各参数的取值范围为:2≤≤8,3≤≤6,2≤≤6。设置初始值如下:0=4 mm,0=6 mm,0=4 mm。
1.3 优化目标
空化效应对超声滚压加工过程中的影响可分为两方面:(1)发生在工件表面附近的空化效应,会产生微射流冲击强化和射流抛光效果,直接改善工件的表面质量;(2)在滚珠周围发生的空化效应,可以冲刷滚珠,从而消除切屑粘连问题,降低摩擦因数,间接提高加工工件的表面质量。
在数值模拟过程中,空化效应的强度无法直接体现。中科院吴鹏飞等人[20]从能量的角度定义了空化强度的概念,可以用气含率作为反映空化强度指标,气含率越高,空化效应越强。由此本文选择滚珠上、、3个关键位置的气含率α、α、α作为优化目标,如图2所示。
由于管内空化过程的复杂性,不易建立流场结构参数与气含率之间的直接联系。但气含率可由Fluent软件在考虑空化效应的两相流模拟过程中计算得出,从而借助近似模型建立两者之间的映射关系。气含率数值计算方法简述如下[19]。
建立二维模型并划分网格。其中,滚珠的超声频振动采用动网格模型,对空化模型通过网格尺寸大小控制计算精度,对边界层网格进行加密。
选择两相流混合模型,湍流模型选择标准的-模型,近壁面处理采用标准壁面函数。选择液态水为流动介质,分别在材料库中添加水和水蒸气(气泡),并设置液态水为主相,水蒸气为次相,在两相相互作用中添加空化模型。本文采用Schnerr-Sauer空化模型,模型的蒸汽生成率e和蒸汽凝结率c方程为:
解析:力臂即点到线的距离。找到支点、力的作用线,再作支点到力的作用线的垂线段。作F的力臂找到支点O及F的作用线,从支点开始向力F的作用线作垂线,并标出力臂L。

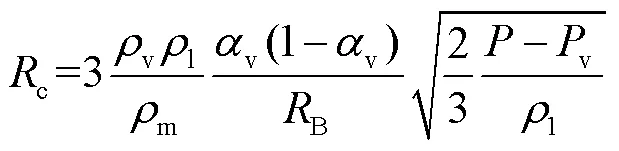
式中:v、l、m分别为气相密度、液相密度和混合相密度;v为气相体积分数(气含率);B为空化泡半径;、v分别为流场压强和空化泡饱和蒸汽压。
通过UDF(User-Defined Function)对滚珠施加纵向超声频振动,其运动形式为=Lsin(2π),其中为超声振动频率,A为振幅。在动网格模型中将编译好的UDF加载到滚珠上。选择压力-速度耦合的求解器,采用SIMPLE算法,压力离散方式选择PRESTO,其余都设置为二阶迎风格式,以提高计算精度。
对模型计算=24.71 kHz时的空化情况。在入口施加101 325 Pa的入口压强;、直接与空气相连,为开放系统,设置为常压。滚珠以正弦运动形式进行超声频振动,数值计算过程将一个正弦振动周期划分为10个时间步。采用4.047 μs的时间步长,迭代500步,即迭代50个周期,时间总长约2 ms。
2 试验设计与近似模型
2.1 试验设计
本文采用最优拉丁超立方设计方法对3个结构变量进行20组方案设计,其优点在于让所有的试验设计点尽可能均匀地分布在设计空间里,具有较好的空间均衡性。利用Fluent数值模拟方法对20组方案进行计算,得到3个关键点的气含率。试验方案和3个关键位置的气含率仿真结果如表1所示。
表1 20组样本点设计方案及气含率计算结果

Tab.1 Design scheme of 20 groups of sample points and calculation results of vapor volume fraction
2.2 优化目标近似模型
采用近似模型不仅能够较好地将优化目标和设计变量关联起来,还可以在一定程度上减小数值计算资源以及提高优化设计效率。本文采用二阶响应面模型,可表述为:

式中:为优化目标;x为结构变量;为待定系数。
由此,基于表1中的20组数据建立结构参数与气含率之间的近似模型为:
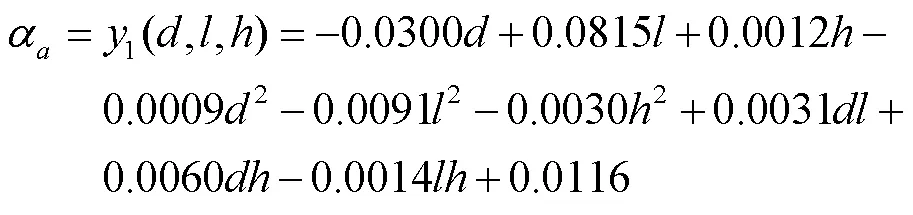
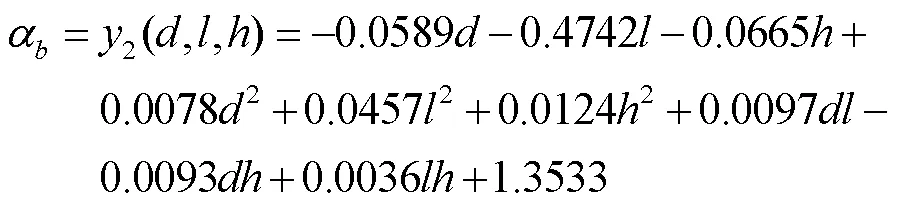

表2 响应面模型检验结果
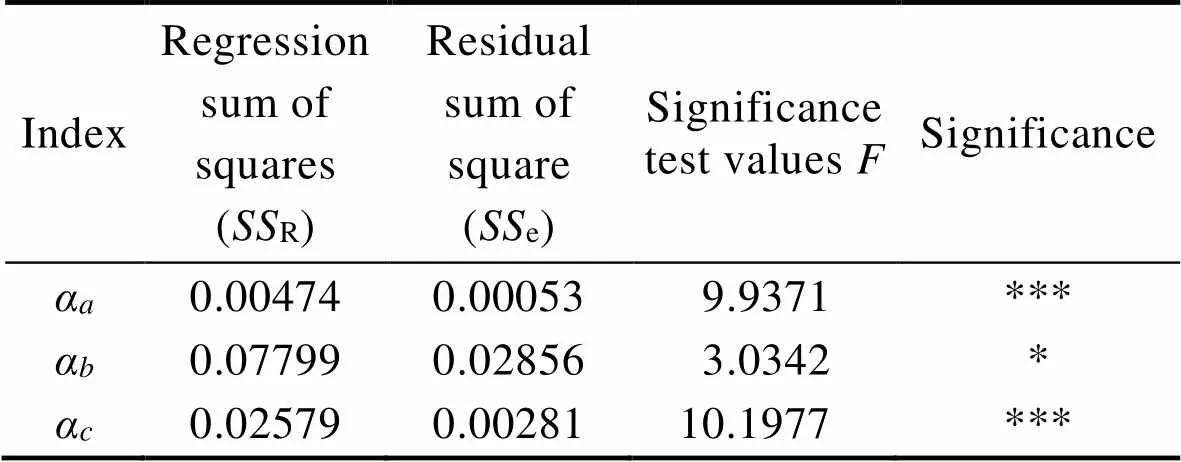
Tab.2 Response surface model test results
Note: “***” indicates significance at the 0.001 level, “*” indicates significance at the 0.05 level.
3 滚压系统流场结构优化
3.1 优化算法与优化目标权重
优化算法选择第二代非劣排序遗传算法NSGA- II,其优点在于探索性能良好,在非支配排序中接近Pareto前沿的个体被选择,使得Pareto前进能力增强。NSGA-II优化过程如图3所示。首先产生一个初始种群,对初始种群进行交叉、变异操作产生子代,然后将父代和子代组成的整体进行非支配和拥挤度排序,并基于精英保留策略选择种群中排名高和拥挤度高的个体组成下一次迭代的父代。如此循环直至迭代结束。

图3 优化算法流程
种群大小设为100,进化代数为30次,交叉概率为0.9,变异周期为10,迁移周期为20。优化过程共优化3000次,以现有装置的结构参数为迭代起始点,之后根据目标函数的优化方向不断搜索最优的结构参数。
优化目标权重的选择对优化结果具有决定性作用。根据决策者的个人经验来确定权重的大小往往会导致优化结果偏离实际全局最优解,而仅从数据出发的客观赋权法则忽略了数据本身的优先级。为了在多目标优化过程中获得合理的目标权重,本文选择基于主观赋权(AHP层次分析法)和客观赋权(熵权法)的组合赋权方法,综合考虑数据本身和主观判断对权重的影响。
3.1.1 AHP确定权重[21-22]
不同位置的气含率对加工的影响不同,对各位置的气含率加权来区分各优化目标的重要程度。加工过程中点位置的空化效应直接作用于加工区域,其空化效应的剧烈程度直接影响加工质量;、两点通过影响滚珠间接影响加工质量。同时位置的空化效应受位置影响[19],则AHP判断矩阵如表3所示。
表3 AHP判断矩阵

Tab.3 AHP judgment matrix
根据判断矩阵计算可得3个优化目标α、α、α的权重分别为0.2014、0.1180、0.6806。判断矩阵的最大特征根为3.025,一致性指标I=0.012,一致性比率R=0.024<0.1,通过一致性检验。
3.1.2 熵权法确定权重[23]
熵权法的基本思路是根据指标变异性的大小来确定客观权重。熵权法基本步骤为:数据标准化;确定评价指标的信息熵E;确定各指标权重W。
由表1所给数据计算可知,3个优化目标α、α、α的信息熵分别为0.9086、0.8588、0.9547,最终由熵权法确定的权重分别为0.3288、0.5083、0.1629。采用乘数归一法对AHP法和熵权法的权值进行耦合,耦合后3个优化目标的权重分别为0.2791、0.2516和0.4692。因此最终的优化模型可表示为:

3.2 优化结果与模拟验证
基于式(4)—(7),采用NSGA-II遗传算法经过3000步迭代计算,得到了最优的结构参数组合。由此重新计算3个关键点的气含率,并与初始值对比,结果如表4所示。可以看出优化后、、3个关键点的气含率都明显提升。相对于初始结构,优化后3个关键点的气含率分别增大21.6%、156.4%和44.1%。对结构参数优化结果进行取整,最终确定最优的空化流场结构参数分别为=8、=6、=6。
表4 优化前后结果对比

Tab.4 Comparison of results before and after optimization
对初始结构和取整后的优化结构进行流场分析,优化结构与初始结构在1.5~2 ms内的气含率变化如图4所示。图4表明优化后结构各个位置的空化强度提升明显。点优化结构与初始结构的气含率变化相同且幅值相差不大。滚珠在位置直接与压力入口相连,滚珠向流场传递的声压极易扩散,较大的压力变化使空化泡在一个滚珠振动周期内生成、膨胀、压缩、溃灭,气泡所能达到的体积有限,气含率较低。即使在不同的流场结构中,空化泡溃灭周期不变,因此流场结构对位置气含率幅值的影响较小。
位置和位置优化结构的气含率相比于初始结构有明显提升。位置和位置的空间相对狭小,压力波不易耗散,空化泡可以在多个超声振动周期不断积累,从而达到一个较高的气含率幅值。流场结构优化后将更有利于空化的发生,气含率可以达到更大的幅值。相对于位置,位置流场更易受流场结构变化的影响,因此优化后的结构能产生更强的空化效应。

图4 初始结构与优化结构下的气含率对比
4 结论
在本研究中,采用有限元分析方法获取超声滚压过程中的气含率,进而构建流场参数和气含率的近似模型,并利用优化算法来进行流场结构优化设计,获取最优结构参数,实现了耦合空化效应的超声滚压系统流场结构优化。
1)采用二阶响应曲面模型准确拟合了流场结构参数和气含率之间的变化关系,为流场结构优化提供了依据。、3个位置气含率的近似模型在95%置信水平上均通过显著性检验。
2)相较于初始流场结构,流场结构优化后滚珠周边3个关键点的气含率分别提升了21.6%、156.4%和44.1%,空化效应明显增强。
[1] BOZDANA A T, GINDY N N Z, LI Hua. Deep Cold Rolling with Ultrasonic Vibrations—A New Mechanical Surface Enhancement Technique[J]. International Journal of Machine Tools and Manufacture, 2005, 45(6): 713-718.
[2] 郑建新, 蒋书祥. 7050铝合金二维超声滚压加工残余应力场研究[J]. 表面技术, 2017, 46(12): 265-269.
ZHENG Jian-xin, JIANG Shu-xiang. Residual Stress Field in the Process of 2D Ultrasonic Rolling 7050 Aluminum Alloy[J]. Surface Technology, 2017, 46(12): 265-269.
[3] LAI Fu-qiang, QU Sheng-guan, LEWIS R, et al. The Influence of Ultrasonic Surface Rolling on the Fatigue and Wear Properties of 23-8N Engine Valve Steel[J]. International Journal of Fatigue, 2019, 125: 299-313.
[4] LIU Hong-wei, ZHENG Jian-xin, GUO Yong-lei, et al. Residual Stresses in High-Speed Two-Dimensional Ultrasonic Rolling 7050 Aluminum Alloy with Thermal- Mechanical Coupling[J]. International Journal of Mechanical Sciences, 2020, 186: 105824.
[5] 唐洋洋, 李林波, 王超, 等. 超声表面滚压纳米化技术研究现状[J]. 表面技术, 2021, 50(2): 160-169.
TANG Yang-yang, LI Lin-bo, WANG Chao, et al. Research Status of USRP Nanocrystallization Technology[J]. Surface Technology, 2021, 50(2): 160-169.
[6] 马梦阳, 李小强, 赖福强, 等. 表面超声滚压加工对配气机构凸轮轴材料滚动接触疲劳性能的影响[J]. 中南大学学报(自然科学版), 2020, 51(9): 2430-2441.
MA Meng-yang, LI Xiao-qiang, LAI Fu-qiang, et al. Effect of Surface Ultrasonic Rolling Processing on Rolling Contact Fatigue Performance of Camshaft Material of Valve Train[J]. Journal of Central South University (Science and Technology), 2020, 51(9): 2430-2441.
[7] WANG Zhen, GAO Chao-feng, LIU Zhong-qiang, et al. Investigation of Microstructural Evolution in a Selective Laser Melted Ti6Al4V Alloy Induced by an Ultrasonic Surface Rolling Process[J]. Materials Science and Engineering: A, 2020, 772: 138696.
[8] ZHANG Meng, LIU Zhi-hua, DENG Jia, et al. Optimum Design of Compressive Residual Stress Field Caused by Ultrasonic Surface Rolling with a Mathematical Model[J]. Applied Mathematical Modelling, 2019, 76: 800-831.
[9] LI Zheng-wei, XU Zhi-wu, MA Lin, et al. Cavitation at Filler Metal/Substrate Interface during Ultrasonic-Assisted Soldering. Part II: Cavitation Erosion Effect[J]. Ultrasonics Sonochemistry, 2019, 50: 278-288.
[10] 叶林征, 祝锡晶, 郭策. 超声空化微射流建模与仿真[J]. 中国机械工程, 2015, 26(21): 2890-2894.
YE Lin-zheng, ZHU Xi-jing, GUO Ce. Ultrasonic Cavitation Micro-Jet Modeling and Simulation[J]. China Mechanical Engineering, 2015, 26(21): 2890-2894.
[11] 梁志强, 马悦, 聂倩倩, 等. 不锈钢微孔超声空化辅助钻削试验研究[J]. 机械工程学报, 2020, 56(1): 205-212.
LIANG Zhi-qiang, MA Yue, NIE Qian-qian, et al. Experimental Study on Ultrasonic Cavitation Assisted Micro Drilling of Stainless Steel[J]. Journal of Mechanical Engineering, 2020, 56(1): 205-212.
[12] 计时鸣, 陈凯, 谭大鹏, 等. 超声空化对软性磨粒流切削效率和质量的影响[J]. 农业工程学报, 2017, 33(12): 82-90.
JI Shi-ming, CHEN Kai, TAN Da-peng, et al. Effect of Ultrasonic Cavitation on Maching Efficiency and Quality of Soft Abrasive Flow[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(12): 82-90.
[13] CHEN Feng-jun, DU Jian-hua, HUANG Shuai. Fabrication of Repairable Anti-Corrosive Superhydrophobic Surfaces with Micro-Nano Structures by Ultrasonic Cavitation[J]. Applied Surface Science, 2021, 541: 148605.
[14] LIEW P J, YAN Ji-wang, KURIYAGAWA T. Fabrication of Deep Micro-Holes in Reaction-Bonded SiC by Ultrasonic Cavitation Assisted Micro-EDM[J]. International Journal of Machine Tools and Manufacture, 2014, 76: 13-20.
[15] 祝锡晶, 叶林征. 功率超声珩磨空化试验分析[J]. 机械工程学报, 2017, 53(19): 136-142.
ZHU Xi-jing, YE Lin-zheng. Analysis of Power Ultrasonic Honing Cavitation Test[J]. Journal of Mechanical Engineering, 2017, 53(19): 136-142.
[16] YE Lin-zheng, ZHU Xi-jing, HE Yan, et al. Surface Strengthening and Grain Refinement of AZ31B Magnesium Alloy by Ultrasonic Cavitation Modification[J]. Chinese Journal of Aeronautics, 2021, 34(4): 508-517.
[17] DING Xiao-long, KANG Yong, LI Deng, et al. Experimental Investigation on Surface Quality Processed by Self- Excited Oscillation Pulsed Waterjet Peening[J]. Materials, 2017, 10(9): 989.
[18] TAN K L, YEO S H. Surface Finishing on IN625 Additively Manufactured Surfaces by Combined Ultrasonic Cavitation and Abrasion[J]. Additive Manufacturing, 2020, 31: 100938.
[19] ZHENG Jian-xin, GUO Yong-lei, ZHU Li-xin, et al. Cavitation Effect in Two-Dimensional Ultrasonic Rolling Process[J]. Ultrasonics, 2021, 115: 106456.
[20] WU Peng-fei, BAI Li-xin, LIN Wei-jun. On the Definition of Cavitation Intensity[J]. Ultrasonics Sonochemistry, 2020, 67: 105141.
[21] SAATY T L. The Modern Science of Multicriteria Decision Making and Its Practical Applications: The AHP/ANP Approach[J]. Operations Research, 2013, 61(5): 1101-1118.
[22] 武春龙, 朱天明, 张鹏, 等. 基于功能模型和层次分析法的智能产品服务系统概念方案构建[J]. 中国机械工程, 2020, 31(7): 853-864.
WU Chun-long, ZHU Tian-ming, ZHANG Peng, et al. Conceptual Scheme Construction of Smart PSS Based on Functional Model and AHP[J]. China Mechanical Engineering, 2020, 31(7): 853-864.
[23] 朱喜安, 魏国栋. 熵值法中无量纲化方法优良标准的探讨[J]. 统计与决策, 2015(2): 12-15.
ZHU Xi-an, WEI Guo-dong. Discussion on the Fine Standard of Dimensionless Method in Entropy Method[J]. Statistics & Decision, 2015(2): 12-15.
Structural Optimization Design of Ultrasonic Rolling System with Coupled Cavitation Effect
,,,,
(School of Mechanical & Power Engineering, Henan Polytechnic University, Jiaozuo 454003, China)
The introduction of cavitation effect in ultrasonic rolling is expected to further improve the reinforcement quality. In order to maximize the cavitation effect, the optimized design of the flow field structure in ultrasonic rolling was carried out. Firstly, software Fluent was used to simulate the cavitation in ultrasonic rolling, and the vapor volume fraction (VVF) at three key locations around the roller was determined. Secondly, the optimal Latin hypercube method was used for the experimental design. The flow field structure parameters were used as the optimization variables, and the VVF at three key locations around the roller was used as the optimization target. The VVF approximate models were established with the second-order response surface method. Then, the weight values of each VVF were determined by combined AHP and entropy weight method, and the optimal flow field structure parameters were obtained by optimal solution of the approximate models using genetic algorithm NSGA-II. Finally, comparison of the VVF obtained with the optimized structure and the initial structure was performed to verify the optimization results. The results showed that the second-order response surface approximate models constructed for VVF fit well based on the results of 20 optimal Latin hypercube tests, and VVF at all three locations passed the significance test at 95% confidence level. After comprehensive analysis, the weights of the three optimization objectives were determined as 0.2791, 0.2516 and 0.4692. Compared with the initial structure, the VVF at the three key positions of the optimized structure was increased remarkably by 21.6%, 156.4% and 44.1%, respectively. The optimized flow structure can be applied to the ultrasonic rolling system to improve the cavitation effect.
ultrasonic rolling; cavitation effect; vapor volume fraction; structure optimization
2021-06-07;
2021-08-26
GUO Yong-lei (1996—), Male, Postgraduate, Research focus: precision and non-traditional machining.
郑建新(1979—),男,博士,教授,主要研究方向为表面工程和精密与特种加工技术。
ZHENG Jian-xin (1979—), Male, Doctor, Professor, Research focus: surface engineering, precision and non-traditional machining.
郭永磊, 郑建新, 朱立新, 等. 耦合空化效应的超声滚压系统流场结构优化设计[J]. 表面技术, 2022, 51(3): 186-191.
v261.8;TG668
A
1001-3660(2022)03-0186-06
10.16490/j.cnki.issn.1001-3660.2022.03.019
2021-06-07;
2021-08-26
河南省重点研发与推广专项(202102210062);河南省高校基本科研业务费专项(NSFRF200309)
Fund:The Key Research and Development and Promotion Program in Henan Province (202102210062); the Fundamental Research Funds for the Universities of Henan Province (NSFRF200309)
郭永磊(1996—),男,硕士研究生,主要研究方向为精密与特种加工技术。
GUO Yong-lei, ZHENG Jian-xin, ZHU Li-xin, et al. Structural Optimization Design of Ultrasonic Rolling System with Coupled Cavitation Effect[J]. Surface Technology, 2022, 51(3): 186-191.
