利用机器学习技术确定同伦分析解中的收敛控制参数

周童晖 柳银萍

摘要： 同伦分析方法是求解强非线性问题解析近似解的有效方法 ， 已被广泛应用于解決科学研究和工程技术中的一些重要问题. 相对于其他已有的解析近似方法 ， 同伦分析方法通过引入若干个辅助参数和辅助函数来控制级数解的收敛区域和收敛速度.针对现有的同伦分析方法中收敛控制参数的选择问题 ， 采用了一种根据机器学习的参数选择算法 ， 首次将同伦分析方法和机器学习技术结合起来 ， 求解非线性数学物理方程收敛性更好的解析近似解. 通过将该算法应用到具体的实例中 ， 可以看出 ， 所获得的同伦分析解明显优于已有的同伦分析解 ， 同时 ， 该算法更具普适性和灵活性.

关键词：同伦分析方法;  辅助函数;  控制参数;  机器学习

中图分类号： O175.14    文献标志码： A    DOI： 10.3969/j.issn.1000-5641.2022.02.005

Determination of convergence control parameters in homotopy analysis solutions based on machine learning technique

ZHOU Tonghui1 ，  LIU Yinping2，3

（1. School of Computer Science and Technology， East China Normal University， Shanghai  200062， China;

2. School of Mathematical Sciences， East China Normal University， Shanghai 200241， China;

3. Shanghai Key Laboratory of PMMP， East China Normal University， Shanghai 200241， China）

Abstract： Homotopy  analysis  method  is  an  effective  method  for  constructing  approximate  analytical solutions to strongly nonlinear problems. The technique has been widely  applied to solve important problems in scientific research and engineering technology. Compared with other existing techniques， this method leverages auxiliary parameters and functions to adjust and control the convergence region and convergence speed of approximate analytical solutions. In this paper， we present a parameter selection algorithm based on machine learning techniques to determine the optimal values of convergence control parameters for homotopy analysis solutions. This marks the first time that homotopy analysis method and machine learning techniques have been combined to obtain approximate analytical method with better convergence for strongly nonlinear mathematical and physical equations. By applying the method to several examples， we show that the convergence of solutions using the proposed method is better than those obtained from existing homotopy analysis methods. In addition， our algorithm is both more universal and flexible.

Keywords： homotopy analysis method;  auxiliary function;  control parameter;  machine learning

0  引言

微分方程是描述自然现象最常用的数学模型.因此 ， 微分方程的解法研究是数学物理领域的常青树 .19世纪以后 ， 线性微分方程的求解方法已经发展得较为成熟 ， 然而自然界中的绝大多数现象都是非线性的.相对于线性微分方程 ， 非线性微分方程的求解要困难得多.现代计算机技术的不断发展和各种数学软件的日益成熟为微分方程的求解提供了强有力的工具.微分方程的解法 ， 根据解的类型可分为：精确解法、数值解法和解析近似解法.由于许多非线性微分方程无法获得其精确解， 因此数值解法是工程技术中常用的方法 ， 但数值解法无法给出解的具体表达形式.

摄动方法[1-3]是一种被广泛使用的解析近似方法 ， 这种方法已被许多杰出的学者用来解决实际工程中的很多问题.但因为摄动法的使用需要系统中有物理小参数 ， 这在很大程度上限制了其适用范围[4-5]. 为了打破这个限制 ， Lyapunov 分解算法和 Adomian 分解法等相继诞生[6-7] ， 这些方法虽然克服了对物理小参数的依赖 ， 但往往解的收敛性没法得到保证. 为了从根本上解决解析近似方法的物理小参数依赖性强和收敛区间小的问题 ， 廖世俊[8]基于拓扑理论中的同伦概念提出了一种新的求解非线性微分方程的解析近似方法—同伦分析方法.该方法不依赖于物理小参数 ， 且总能将非线性问题转化为一系列的线性子问题 ， 通过自由选取线性算子和基函数列 ， 方便了线性子问题求解 ， 并且能通过辅助参数和辅助函数来控制级数解的收敛区域和收敛速度 ， 确保所获得的解析近似解具有较高的精度.该方法引起了国内外很多学者的关注 ， 这些学者的不断探索和研究使得同伦分析方法的理论基础更加牢固 ， 例如 ， Odibat[9]给出了同伦级数解收敛的一个充分条件 ， Yabushita 等[10]使用余量的平方度量近似解析解的準确度.文献[11-12]初步研究了辅助线性算子和收敛控制参数的选取.赵银龙[13]通过定义逆算子进一步提高了高阶形变方程的求解效率等.

本文将同伦分析方法和机器学习技术相结合 ， 首先 ， 应用同伦分析方法求得非线性系统的m （m >0）阶带参数的解析近似解.然后 ， 将所获得的解代入非线性微分方程中 ， 进一步将所获得的余量作为目标函数 ， 采用机器学习技术中常用的小批量梯度下降法（Mini-Batch Gradient Descant）进行优化[14] ， 获得余量最优的参数值. 最后 ， 获得原方程精度很高的解析近似解.本文所提出的方法不仅可以通过训练集范围来调节解析近似解在不同的自变量区间的逼近效果 ， 还可以同时对多个参数进行优化.另外 ， 对于部分算例 ， 本文将辅助函数进行了二阶加权展开 ， 以此来获得更优的辅助函数和收敛性更好的解析近似解.实验表明， 对于大部分非线性方程， 本文所提出的方法可以获得精度更高的解析近似解.

1  算法原理

1.1  同伦分析解的构造思路简述

考虑一个非线性微分方程

N[u（x）]= 0. （1）

式（1）中： N 为非线性微分算子; u（x）为所要求解的未知函数. 该系统中可能还包含若干个未知的物理参数 ， 如频率、振幅等. 采用同伦分析方法求解式（1）， 首先要构造所谓的零阶形变方程

（1− q）L[Φ（x， q）− V0（x）]= qhH（x）N[Φ（x， q）].  （2）

式（2）中： L 为辅助线性算子; h 为辅助参数; H（x）为辅助函数;Φ（x， q）为 x， q 的函数; V0（x）为初始猜测解; q ∈[0， 1]为嵌入参数. 由式（2）可知 ， 由于 h  0且 H（x）  0 ， 当 q =0 时 ， 式（2）的解为Φ（x， q）= V0（x）;当 q =1 时 ， 式（2）的解变为Φ（x， 1）= u（x）. 由此可见 ， 当 q 从0 变化到1 时 ， Φ（x， q）从初始猜测解演化到u（x）. 根据泰勒展开定理 ， 将Φ（x， q）关于q 展开成如下幂级数

（3）

令

Vi（x）=  i！·     ∂qi       q=0 ， （4）

根据式（4）， 可将式（3）简化为

Φ（x， q）= V0（x）+  Vm（x）qm .

利用Φ（x， 1）= u（x） ， 可得到解的级数展开式

u（x）= V0（x）+  Vm（x）.

对零阶形变方程式（2）的两边关于q 求m 阶导数 ， 再令q =0 ， 得到m 阶形变方程

式（5）中：

Rm（Vm −1）= （m −1）！·       ∂qm −1          q=0;

依次迭代求解高阶形变方程（5）， 则可得到u（x）的m 阶解析近似表达式

式（6）即为所求系统的 m 阶解析近似解.需要说明的是 ， 所获得的解中含有收敛控制参数和辅助函数 ， 收敛控制参数可以调节和控制解的收敛区域和收敛速度 ， 辅助函数可以确保所获得的解符合解表达法则. 另外 ， 式（6）的解中可能还包含有系统中未知的物理参数 ， 如何确定式（6）的解表达式中的未知参数和未知函数 ， 使所获得的解收敛性更好呢？同伦分析方法本身提供了若干个法则来确定解中的未知物理参数 ， 但是该思路并不具有普适性， 需要针对不同的系统进行分析.本文将机器学习技术应用到同伦分析方法中 ， 应用机器学习技术中的小批量梯度下降法来确定同伦分析解中的未知参数 ， 以获得收敛性较好的解及系统中未知的物理参数值.

1.2  利用机器学习的收敛控制参数确定算法

在上述算法所获得的同伦分析解中包含有未知的收敛控制参数和辅助函数 ， 也可能包含未知的物理参数. 如何确定这些未知参数和未知函数？本文应用机器学习方法中的小批量梯度下降法对同伦分析解中的未知参数进行优化.

令θ= {h， ω} ， h 为式（2）中出现的辅助参数 ， ω表示线性辅助算子 L 、初始猜测解 V0（x）以及辅助函数 H（x）中用以加速收敛与控制收敛范围的其他控制参数 ， 该集合中也可能会包含其他的未知参数. N[V（x0， θ）]2作为余量的平方度量了以上解析近似解 V（x0， θ）趋于u（x0）的程度 ， 当 N[V（x0， θ）]2 →0 时 ， 有V（x0， θ）→ u（x0） ， 因此最小化rΩN[V（x， θ）]2dx 得到的θ可以使解析近似解收敛得更快、更好.定义目标函数

式（7）中x ∈Ω ， Ω是训练集取值集合 ， 其为定义域的真子集.

继而问题转化为对式（7）中θ的优化 ， 考虑到利用 ReLU （Rectified Linear Unit）函数进行梯度截断来解决梯度爆炸问题会导致训练数据分布不均 ， 且函数需要的参数自适应性能力弱 ， 本文使用 Adam 梯度下降法避免这一问题[15] ， 解决梯度爆炸问题的同时也加速了收敛 ， 如算法1 所示.

算法1 梯度下降法

输入：训练集 X

输出：迭代优化后的参数θ

1：初始化学习参数ρ1 =0.9 ， ρ2 =0.999 ， δ= 10−8 ， 迭代参数 k =1 ， s0 =0 ， r0 =0 ， 最高迭代次数 K

2：生成随机点数据集 X ⊆Ω

3：设定学习率α ， 初始参数θ0

4： Repeat

5：随机选取训练集的子集Xk = {x1， x2 ， ·· · ， xn} ， Xk ⊆ X

6：计算梯度： g =  ∇θk J （xi， θk）

7：计算一阶矩和二阶矩 sk+1 =ρ1sk + （1− ρ1）g， rk+1 =ρ2rk + （1− ρ2）g · g

8：修正一阶矩和二阶矩： s^=  ， r^=

9：以一阶矩为梯度 ， 用二阶矩调整学习速度 ， 更新参数：θk+1 =θk −  s^

10：k = k +1

11： Until k ⩾ K  or θ收敛

本文方法利用 Python 的流处理框架 Tensorflow， 方便进行算法策略的调整， 训练集根据非线性系统的定义域Ω ， 生成指定范围内的64位浮点数.

2  应用实例

例1  考虑无量纲化后的空气中自由下落球体方程

根据式（8）定义非线性算子

N[Φ（t， q）]=           +Φ2（t， q）− 1.

选择解表达形式

选取线性算子 L， 辅助函数 H 和初始猜测解 V0分别为

应用同伦分析方法 ， 依次迭代求解高阶形变方程 ， 获得近似解的前 m 项：

从而得到带参数的近似解

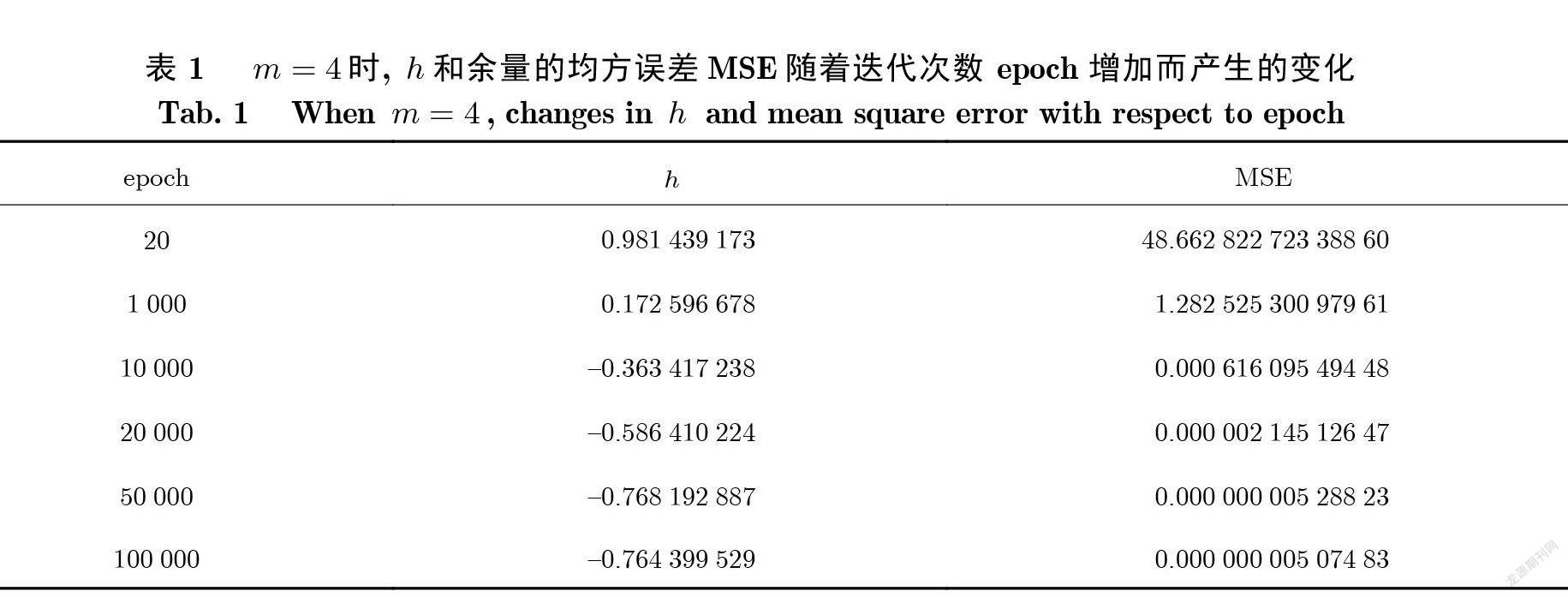
取 m =4所得的解析近似解表达式 ， 使用梯度下降的 Adam 算法优化 ， 设初值h =1 ;单次迭代点集大小 n =50; 学习率 a =1.0× 10−3; 训练集范围为（0， 1）. 经过约4 ×105次迭代 ， h 收敛于 –0.764附近 ， 选取验证集误差最小的h =−0.7644 .表1给出了m =4 时 ， h 和余量的均方误差 MSE （Mean Squared Error）随着迭代次数增加而产生的变化 ， 表2将本文所获得的解析近似解与文献[4]中所获得的解析近似解（h =− 1）及精确解的平均绝对误差 MAE （Mean Absolute Error）进行比较.

从表 1可知， 随着迭代次数的增加， h 的值趋于收敛 ， 且余量的均方误差 MSE也随之显著下降.从表 2可知 ， 本文所获得的解析近似解明显优于文献[4]中的解析近似解 ， 并且本文所获得的解析近似解的平均绝对误差明显小于文献[4]中的解析近似解的平均绝对误差.

例2  考虑空间 Duffing 振子满足的非线性方程

式（9）中 L 为边界条件常量. 引入变换

在该变换下 ， 方程（9）转换为

v′′（x）+ ε（v − v3）= 0， v（0）= v（π）= 0.

假设 A 为波的振幅 ， 令v（x）= Au（x） ， 则得到

式（10）中A = v（π/2）. 对非线性系统（10）应用同伦分析方法求解 ， 定义非线性算子

N[Φ（x， q）， α（q）]=             +ε（Φ（x， q）− α2（q）Φ3（x， q））.

对该系统构造零阶形变方程

当q 从0 变化到1 时 ， α（q）从初值 A0演化到 A .根据非线性算子的性质 ， 选用以下解表达形式

u（x）=  bisin[（2i +1）x].（11）

根據解表达式（11）， 定义辅助线性算子 L 和选取初始猜测解 V0（x）为

L[Φ（x， q）]=             +Φ（x， q），

式中线性算子具有性质 L（C1sin x + C2cos x）= 0 ， C1 ， C2为任意常数. 对该非线性系统 ， 文献[4]给出了多个可行的辅助函数

H（x）= 1， H（x）= sin2x， H（x）= cos2x， H（x）= cos（2x）.  （12）

本文将式（12）中的可选 H（x）作基函数加权展开 ， 去除其中的线性相关项 ， 得到假设形式

例2 中除了要求u（x） ， 还要求出振幅 A .故除了对Φ（x， q）进行泰勒展开 ， 同样地需要对α（q）进行泰勒展开

由此可得到高阶形变方程

式（14）中

Rm（Vm −1， Am −1）= （m −1）     ∂qm −1  q=0.

由于h 总是以hH（x）形式出现在解分量中 ， 故令h =1 即可.当C1 =0 时 ， 对C0进行训练等价于当 H（x）= 1时对h 进行训练.

根据解表达形式与同伦分析方法的解封闭原则[4] ， 式（14）的右端不应含有 sin x 项 ， 在求解第 i 阶形变方程之前 ， 通过令sin x 项的系数为零得到关于Ai −1 的代数方程 ， 求解该方程即可确定 Ai–1 ， 然后根据高阶形变方程（14）求解Vi（x） ， 这样即可获得该系统的解析近似解及振幅 A 的近似值.

令ε= 10 ， m =4 ， 求得4 阶解析近似解后 ， 使用基于梯度下降的 Adam 算法进一步确定解表达式中的未知参数. 构造目标函数并设置相关参数：单次迭代点集大小n =50; 学习率a =1.0× 10−4; 参数x ∈（0， 1） ， 训练集大小为106.

在式（13）中 ， 令 C1 =0得到一阶辅助函数 H（x）= C0 ， 选择最优误差对应的参数 C0 =−0.439 ， 对于二阶辅助函数 ， C0和 C1分别收敛于−0.56035346和 −0.41409920附近 ， 将所得结果代入所得的解析近似解中， 得到基于不同辅助函数的余量平方曲线（ 图1）.

从图 1可以看出梯度下降法在选择控制参数的最优值时更具优越性 ， 特别地 ， 基于二阶展开的辅助函数所获得的近似解精度更高.

根据解表达式（11）可知 ， 近似解是周期 T =2π的奇函数 ， 所以在（0， π）上进行参数训练即可获得定义域上的最优参数结果. 表3列出了本文根据不同训练集得到的参数结果 ， 比较了其对应余量函数的定积分 ， 其中{C0， C1}（a，b）表示在训练集（a， b）上训练得到的最优化参数值的集合.

从表3可知 ， 可通过选择不同训练集区间 ， 调整收敛控制参数 ， 从而获得相应区间内的最优近似解.

例2 验证了本文所提出的二阶加权展开的辅助函数对于近似解收敛性的进一步优化 ， 并使用本文的方法进行参数选择 ， 得到了比文献[4]中的单一辅助参数选择后的近似解更优的结果. 通过对不同训练区间上的近似解结果进行余量积分的比较 ， 证明了本文算法的确可以根据不同训练区间来寻找相应区间内更优的解析近似解.

例3  考虑具有奇非线性保守系统的自由振动方程

式（15）中：ε 为人工小参数; a 为振幅. 假设 w 为频率 ， 引入变换x = wt ， U（t）= u（x） ， 则非线性系统（15）转换为

（16）

根据非线性算子的性质选取解表达形式

u（x）=  bicos（ix）.（17）

式（17）中bi为待定系数. 进一步选取辅助线性算子与初始猜测解

L[Φ（x， q）]= w [+ Φ（x， q）] ，     （18）

V0（x）= acos x.   （19）

式（18）中线性算子具有性质 L（C1sin x + C2cos x）= 0 ， C1 ， C2为任意常数. 根据解表达形式可知辅助函数具有以下形式

H（x）= cos（2kx），  k =0， 1， 2， 3， ·· ·.

将 H（x）利用基函数列进行加权展开为

H（x）= C1+ C2cos（2x）.  （20）

与例2 的求解思路相同， 根据式（16）—（20）求出u（x）的m 阶解析近似解.

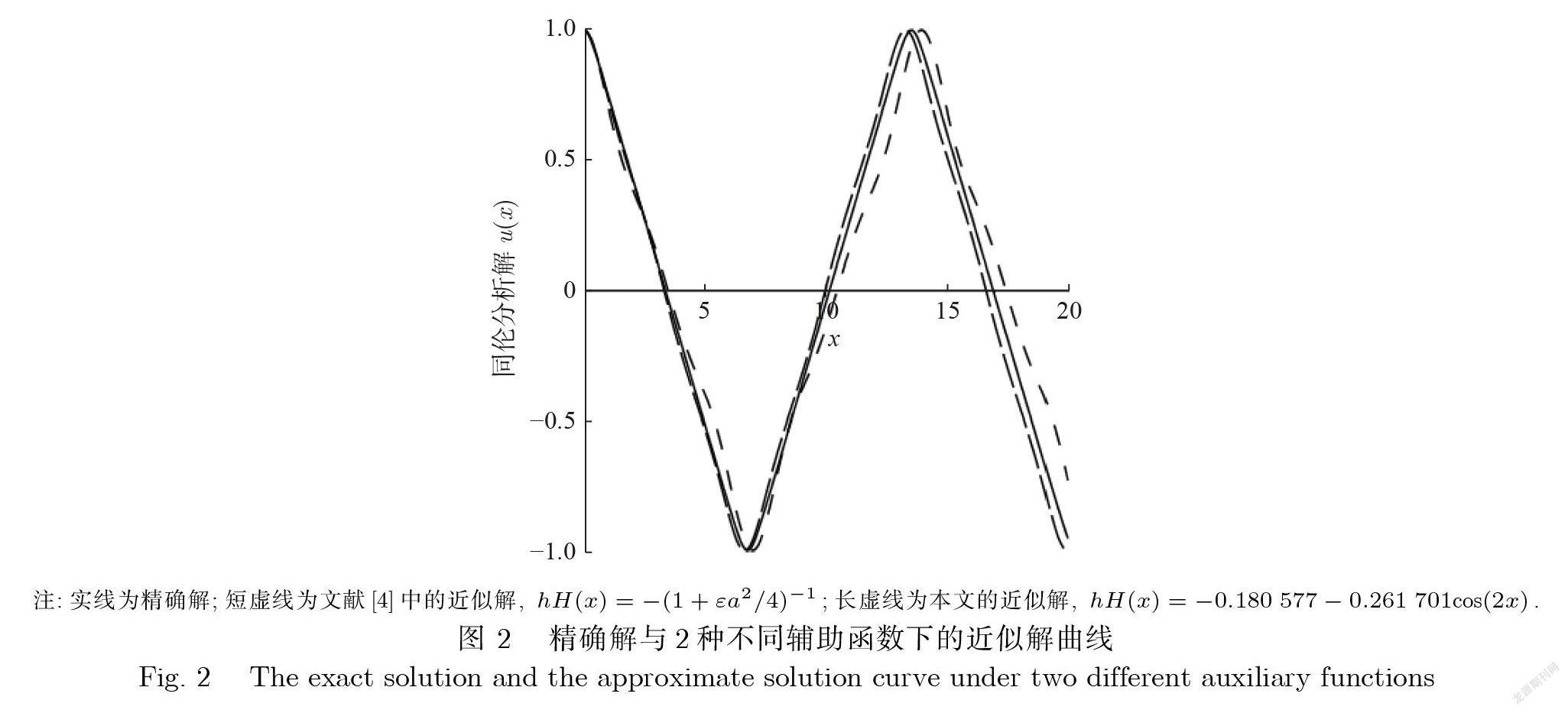
令ε= 10 ， a =1 ， m =4 ， 设初值C0 =1 ， C1 =1 ;单次迭代点集大小n =50; 学习率a =1.0× 10−3; 训练集范围为（0， 20）;训练集大小为106; 训练选取最小验证集均方误差对应的结果C0 =−0.180577，C1 =−0.261701. 图 2将本文结果与文献[4]中的单一同伦分析解进行了比较.

从图 2可知， 本文所获得的解析近似解较文献[4]中的同伦分析解具有更高的精度.该实例所获得的结果进一步验证了基于二阶加权展开辅助函数所获得的同伦分析解具有更好的收敛性.

例4 考虑 Thomas-Fermi 方程

根据渐进性质分析[16-17] ， 引入变换

式中λ 为引入参数. 则方程（21）转换为

利用文献[13]中引入的多个收敛控制参数 ， 使用解表达式（23）， 初始猜测解式（24）， 辅助线性算子式 （25）和辅助函数式（26）， 其中辅助线性算子式（25）是文献[13]中带参数辅助线性算子优化后的结果， 本文着重对引入的控制参数λ ， ε以及辅助参数h 进行优化.

式中：辅助线性算子（25）具有性质 L（tj）= 0 ， j =15 ， −3 ， −4.

根据式（22）—（26）， 利用同伦分析方法可求出 g（t）的 m 阶近似解 gm（t） ， 根据变换 um（x）= g （1+ λ） 得到u（x）的m 阶近似解

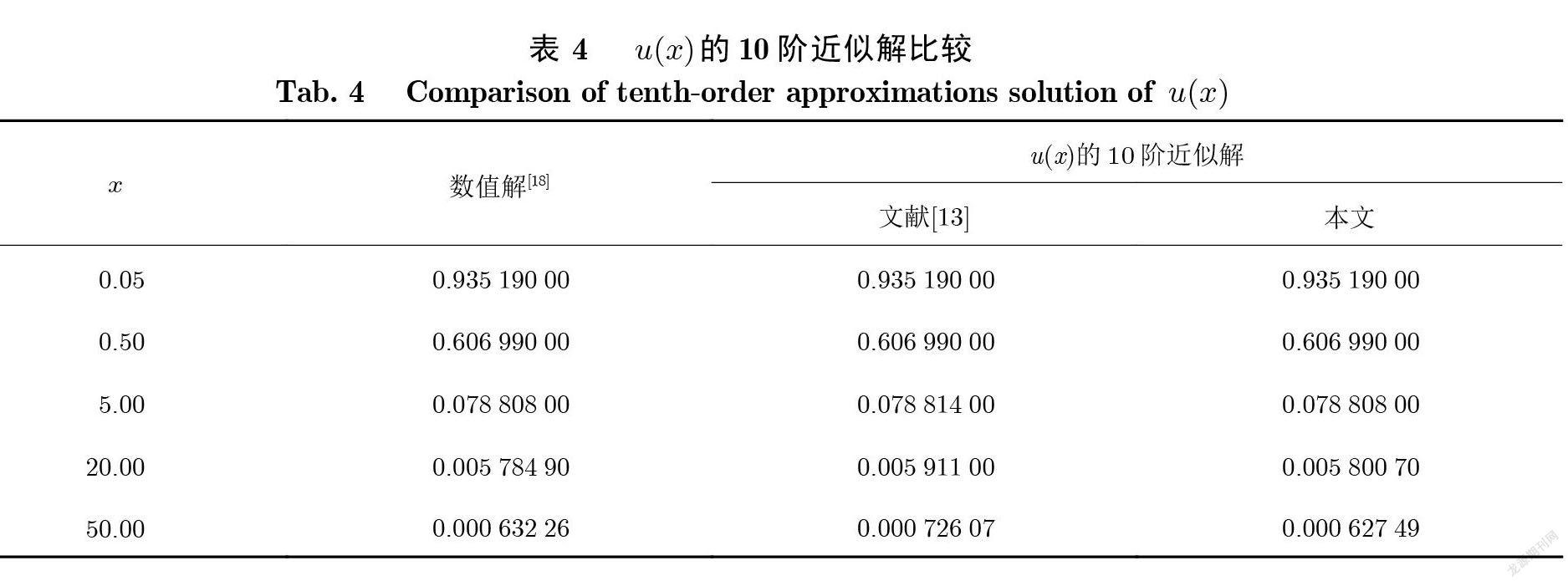
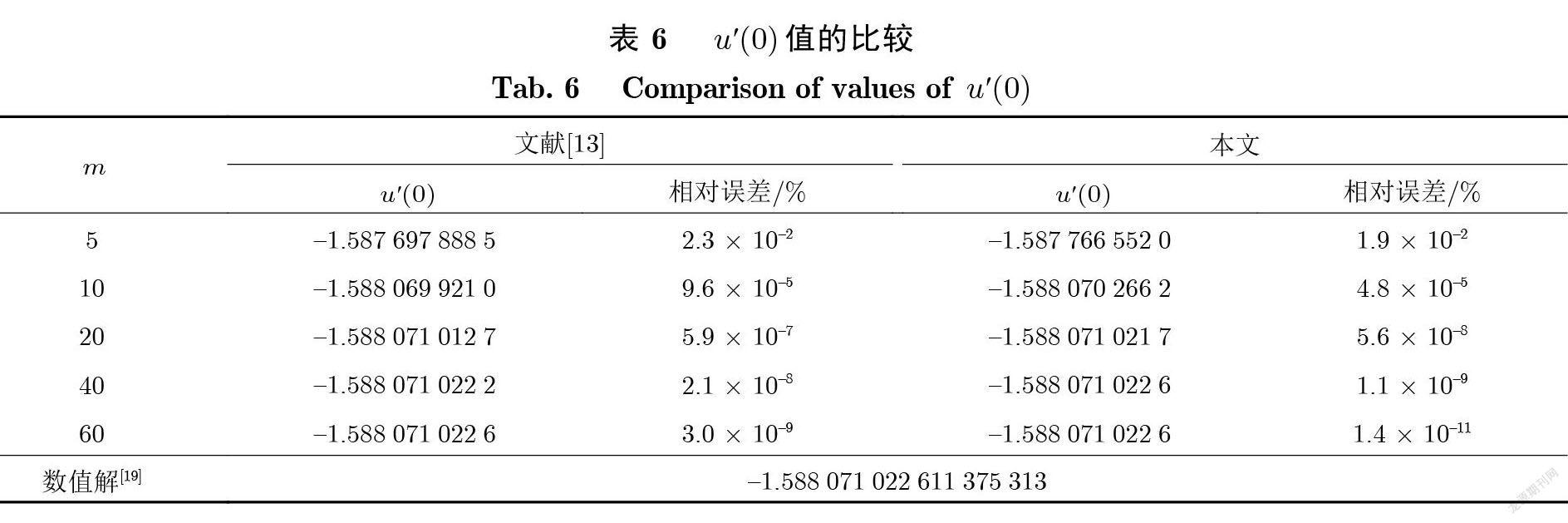
文献[13]利用约2 000个间隔点的误差和构造了关于控制参数的函数 ， 并根据 Mathematica 中的 Nminimize 命令獲得了最优结果λ= 5/16 ， ε= −86/17 ， h =− 11/8. 本文取m =6 的解析近似解表达式 ， 设初值 h =1 ， ε= −1 ， λ= 1; 单次迭代点集大小n =10; 学习率a =1.0× 10− 1; 训练集范围为 （0， 100）. 例4 使用负幂级数表示解 ， 为了使结果更精确 ， 例4 在训练时将梯度修改为x2g ， 通过这种等价于修改训练集概率密度的方式 ， 解决了x 较大时 N[u（x， θ）]对θ的导数过小而导致的均方误差有效数字溢出问题. 在此调整的基础上 ， 训练得到验证集均方误差最小时所对应的参数λ= 0.33546 ， ε= −4.4623677 ， h =− 1.360267. 表 4比较了选定点上数值解、文献[13]近似解和本文近似解 ， 表 5比较了本文近似解与文献[13]中近似解在选定点上的均方误差， 表 6给出了本文近似解得到的导数值u′（0）与文献[13]中相应结果的比较 ， 注意由于例4 所使用的解表达是负幂级数的形式 ， 需要进行高精度计算， 表 4—6的结果都是在 Maple 2018高精度环境下计算得到.

从表 4—6 可知 ， 本文所获得的同伦分析解要优于文献[13]中的同伦分析解.例 4基于文献[13]中所引入的多个收敛控制参数 ， 同时对同伦分析解中的多个参数进行优化 ， 计算结果表明 ， 本文所提出的方法在确定参数的最优值时较文献[13]中所使用的方法更具普适性和灵活性.

3  总结

同伦分析方法是构造非线性微分方程解析近似解的有效方法 ， 该方法最大的优点在于通过引入控制参数来调节和控制级数解的收敛区域和收敛速度 ， 但控制参数的选择缺少系统的方法 ， 本文使用机器学习技术来确定控制参数的最优值. 计算结果表明 ， 基于本文算法所得到的参数值在级数解的收敛速度上有更好的表现 ， 这为同伦分析方法的参数确定开拓了一种新的途径 ， 并且机器学习算法的发展非常迅速， 因此， 本文所提出的参数选择算法具有较好的发展和应用前景.

[参考文献]

[1] VAN DYKE M. Perturbation Methods in Fluid Mechanics [M]. Stanford： Parabolic Press， 1975.

[2] NAYFEH A H. Introduction to Perturbation Techniques [M]. New York： John Wiley & Sons， 1981.

[3] NAYFEH A H. Perturbation Methods [M]. New York： John Wiley & Sons， 2008.

[4] LIAO S J. Beyond Perturbation： Introduction to the Homotopy Analysis Method [M]. Boca Raton， Florida： CRC Press， 2004.

[5] LIAO S J. Homotopy Analysis Method in Nonlinear Differential Equations [M]. Beijing： Higer Education Press， 2012.

[6] LYAPUNOV A M. The general problem of the stability of motion [J]. International Journal of Control， 1992， 55（3）：531-534.

[7] ADOMIAN G. Nonlinear Stochastic Operator Equations [M]. Orlando： Academic Press， 1986.

[8]廖世俊.求解非线性问题的同伦分析方法[D].上海：上海交通大学， 1992.

[9] ODIBAT Z M. A study on the convergence of homotopy analysis method [J]. Applied Mathematics and Computation， 2010， 217（2）：782-789.

[10] YABUSHITA K， YAMASHITA M， TSUBOI K. An analytic solution of projectile motion with the quadratic resistance law using thehomotopy analysis method [J]. Journal of Physics A： Mathematical and Theoretical， 2007， 40（29）：8403-8416.

[11] LIAO S J. Advances in the Homotopy Analysis Method [M]. Singapore： World Scientific， 2014.

[12] VAN GORDER R A， VAJRAVELU K. On the selection of auxiliary functions， operators， and convergence control parameters in theapplication of the homotopy analysis method to nonlinear differential equations： A general approach [J]. Communications in Nonlinear Science and Numerical Simulation， 2009， 14（12）：4078-4089.

[13] 赵银龙.同伦分析方法之改进及其在非线性边值问题之应用[D].上海：上海交通大学， 2015.

[14] ROUX N L， SCHMIDT M， BACH F. A stochastic gradient method with an exponential convergence rate for finite training sets [EB/OL].（2013-03-11）[2020-07-26]. https：//arxiv.org/pdf/1202.6258.pdf.

[15] KINGMA D P， BA J L . Adam： A method for stochastic optimization [EB/OL].（2015-07-23）[2020-08-27]. https：//arxiv.org/pdf/1412.6980v8.pdf.

[16] FEYNMAN R P， METROPOLIS N， TELLER E. Equations of state of elements based on the generalized Fermi-Thomas theory [J].Physical Review， 1949， 75（10）：1561-1573.

[17] COULSON C A， MARCH N H. Momenta in atoms using the Thomas-Fermi method [J]. Proceedings of the Physical Society， 1950，63（4）：367-374.

[18] KOBAYASHI S， NAGAI S， UMEDA K. Accurate value of the initial slope of the ordinary TF function [J]. Journal of the PhysicalSociety of Japan， 1955， 10（9）：759-762.

[19] FERNÁNDEZ F M. Rational approximation to the Thomas-Fermi equations [J]. Applied Mathematics and Computation， 2011，217（13）：6433-6436.

（責任编辑：陈丽贞）