基于电流信号的振动电机轴承故障检测

孟东容， 段志善

(1. 西京学院机械工程学院，陕西 西安 710123; 2. 西安建筑科技大学机电工程学院，陕西 西安 710055)

0 引 言

振动电机作为动力源，常用于矿产、冶金、电力、煤炭等行业[1]。工作环境通常伴随有粉尘、渣石等影响电机寿命的外界因素，其寿命决定了振动机械的运转状态和安全系数。因此，对振动电机常见故障进行准确检测和预判具有重要的意义。

振动电机常见的故障类型与普通三相异步电动机相似，包括转子断条、定子匝间短路、气隙偏心和轴承故障等。由于振动电机与普通电机结构有所不同，因此故障特征频率不能简单套用。孟东容等[2]对振动电机的转子断条和气隙偏心故障机理进行了分析，通过检测定子电流能够判断其故障类型与程度，但并没有针对轴承故障进行进一步分析；Peter[3]将普通三相异步电机的轴承故障分类为外滚道故障、内滚道故障、滚动体故障和保持架故障，并给出了相应的故障频率，但这些频率并不适用于振动电机的轴承故障诊断；Schoen等[4]建立了斯科恩模型，通过采集定子某相电流，分析得出了轴承故障特征频率，但该频率是在假设转子没有变形的前提下进行的。以上研究均没有对振动电机的轴承故障提出明确的机理分析和检测方法。

目前滚动轴承故障可通过多种信号进行检测和预判，如油液信号、声音信号、振动信号、油膜电阻信号和定子电流信号等[5]，当前基于振动信号检测的方法研究较多，但对振动机械来说，振动信号通常比较微弱，极易淹没在噪声中，并且计算复杂、处理速度慢。因此对于振动电机的轴承故障应采用非振动信号的故障特征检测才有更大的优势。本文通过检测定子某相电流信号来判断振动电机轴承故障类型及其程度。

1 轴承故障模型

本文研究滚动轴承结构如图1所示。轴承由外滚道、内滚道、滚动体和保持架组成。其中，滚动体在内外滚道之间滚动，保持架以保持相邻滚动体之间的距离。

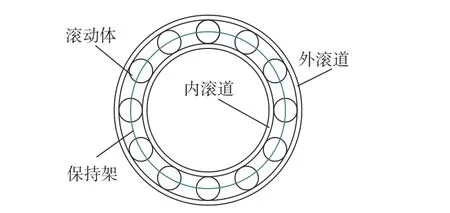
图1 振动电机滚动轴承示意图

轴承故障类型分为一般粗糙度缺陷和单点缺陷两种，一般粗糙度缺陷会使振动信号或电流信号中产生不可预期频带宽度[6]，而单点缺陷会产生对应的故障频率，凹陷、小孔等都是基本的单点缺陷，本文以轴承单点缺陷为研究对象。

轴承的单点缺陷可发生在轴承外滚道、内滚道和滚动体中。无论是哪种故障类型都会产生一定周期的振动，对应不同位置的特征频率如下：

式中：fr——转子旋转频率；

Nb——滚动体个数；

Db——滚动体直径；

Dc——滚道节径；

β——接触角(滚动轴承中套圈与滚动体接触处的法线和垂直于轴承轴心线平面间的夹角)。

传统故障检测方法以检测分析振动信号为主，单点缺陷故障分析模型在文献[7-9]中均有应用，文献[10]给出了上述模型的详细推导过程。

Schoen等[4]认为轴承故障产生的振动会导致气隙磁通密度的变化，从而产生与电源频率、振动频率有关的电流，并提出了利用电动机定子电流信号分析轴承故障的斯科恩模型。当轴承发生故障时，在定子电流中会产生额外的频率fbf=|fs±kfc|，其中fs是电源频率，k=1，2，3,···,fc是轴承故障特征频率。由于振动电机结构特殊，其轴承受力、气隙磁通密度变化规律与普通电机存在较大差异。因此，在振动电机定子电流中产生的特征频率也必然会有所不同，本文应用斯科恩模型对振动电机轴承外圈缺陷故障的特征进行了详细分析。

2 振动电机轴承受力分析

电动机轴承安装方式与负载形式有关，一般来说，普通电机所受外力的方向是不随时间变化的，其外圈与滚动体配合处受力不一致，时间过长将会影响轴承寿命。因此，安装时采用内圈与电机轴过盈配合，外圈与轴承座间隙配合。振动电机转轴两端伸出并加载对称偏心块，电机旋转产生偏心力矩，激振力方向随时间变化如图2所示。其外圈受力是一致的，轴承内圈受力不变，因此，安装要求与普通电机正好相反，轴承与端盖不能产生相对滑动，轴承与电机轴间隙配合[11]。

图2 不同时刻的激振力方向

现假设轴承外圈有一单点缺陷如图3所示，并且轴承按照上述方式进行安装，可知激振力的方向随时间变化，而单点缺陷位置并不发生变化，激振力F与缺陷位置会发生周期性的重叠，将产生与转轴旋转频率有关的特征频率。振动电机轴承在运转过程中，其外圈受滚动体压力的受力点是随时间变化而变化的。轴承外圈的载荷区域变化情况如图3所示。

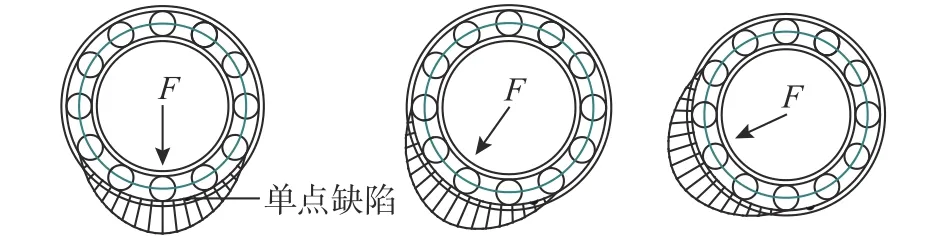
图3 轴承外圈载荷区域变化情况

由图3可知，电机运行中当滚珠恰好位于单点缺陷位置区域时，将会造成气隙的周期性变化。

3 振动电机轴承故障理论分析

3.1 气隙长度计算

振动电机运行时，电动机转子两端伸出且会受到较大的离心力，从而使转子产生弯曲变形，其变形程度与激振力大小和主轴尺寸、材料等有关，导致了振动电机气隙大小会沿着轴向产生变化，现假设轴承故障为外圈缺陷，图4显示了振动电机某一时刻在激振力和产生单点缺陷综合影响后的气隙长度。

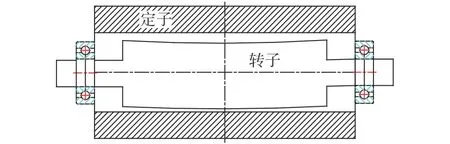
图4 振动电机在轴承单点缺陷时的气隙变化

正常情况下，定转子之间的空气隙长度是不变的。由图4可知，振动电机在发生外圈缺陷时，其气隙的变化由两部分构成：转子变形引起的气隙变化和外圈缺陷引起的气隙变化。振动电机在较大激振力下运行时转子形变会导致电机发生非线性气隙偏心[2]，轴承外圈故障导致的气隙变化，由静态偏心率和狄拉克函数构成[11-12]。

3.2 气隙磁导率计算

3.3 气隙磁通密度计算

由式(7)可知，当振动电机轴承外圈出现局部缺陷时，对磁通密度产生了影响。在磁通密度中除了基本的正弦波外还有与故障有关的正弦波。即除了出现电源频率fs，还出现了轴承外圈故障频率fc和转子旋转角频率fr。

3.4 分析定子电流

4 仿真分析

4.1 仿真模型建立

4.2 影响因素分析

在仿真过程中需要提供的参数有定子电路电阻、转子导条电阻、端环电阻、导条电感、端环电感等，将上述两个模型的参数分别输入S函数中进行仿真，仿真时长均为60 s，提取模型中的三相交流电数据并进行快速傅里叶变换(FFT)得到三相交流电的频谱图，取三相电中的A相进行分析。仿真结果如图5～图7所示。

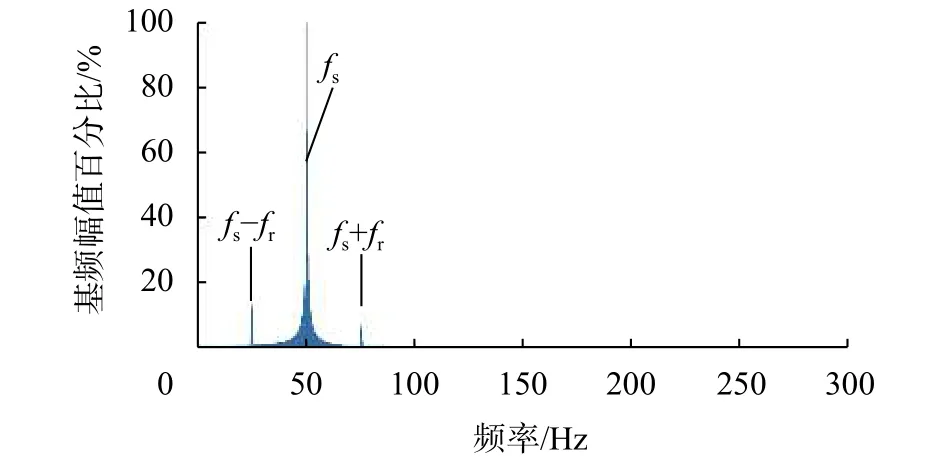
图5 振动电机正常运行时的电流频谱

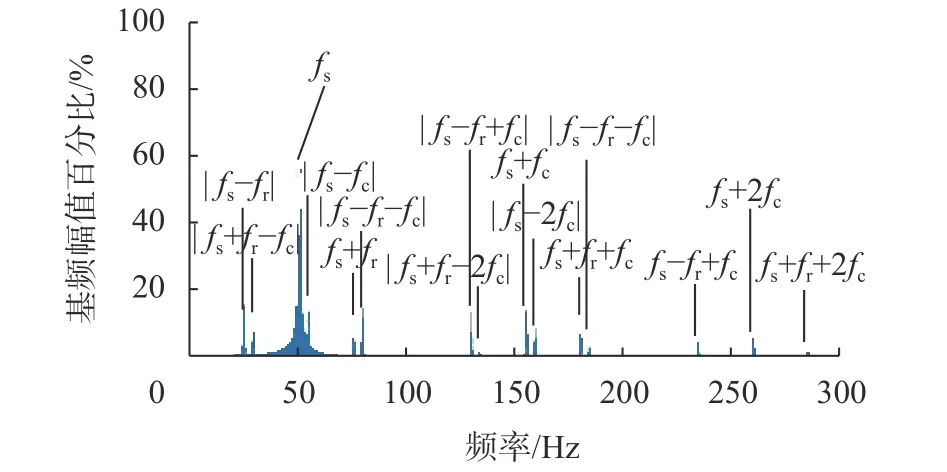
图6 模型1轴承外圈单点缺陷时的电流频谱

图7 模型2轴承外圈单点缺陷时的电流频谱

由图5可知，振动电机正常运行时的电流除电源频率fs外 还有fs±fr的特征频率，由图6和图7可看出，对两种型号的振动电机在外圈单点缺陷的情况下进行仿真时，电流的频谱中会出现fzc=|fs±mfr±kfc|的故障特征频率，仿真结果均与理论计算结果一致，说明当电阻、电感、旋转频率、轴承参数等影响因素发生变化时，该方法仍具有一定的普适性。因此对这些特征频率的实时监测和在线分析能够预测振动电机轴承外圈故障并及时进行维护。

5 结束语

振动电机与普通电机结构、受力、振动周期等有明显区别，因此普通电机的轴承故障特征不能直接用来诊断振动电机的轴承故障，通过分析振动电机轴承受力，建立了振动电机外滚道单点缺陷时的气隙动态模型，计算了气隙磁导、气隙磁密，分析了定子电流频率，得到以下结论：

1)振动电机发生外滚道单点缺陷时，在振动电机电源电流中会感生故障特征频率为fzc=|fs±mfr±kfc|的电流，其中m=0或1，k=1，2， 3 ···，该频率可作为振动电机外圈缺陷故障的判断依据。

2)通过Matlab仿真分析了两种型号振动电机轴承外圈单点缺陷时的电流频谱，所得结果与理论分析一致，该方法为振动电机轴承内滚道、滚动体单点缺陷及混合缺陷时的故障诊断提供了理论依据和模型参考。