角接触球轴承旋转精度数值仿真分析*
2022-01-27王晓明余永健王东峰薛玉君李济顺
王晓明,余永健,王东峰,薛玉君,2,李济顺
(1.河南科技大学机电工程学院,洛阳 471003;2.河南省机械设计及传动系统重点实验室,洛阳 471003;3.洛阳轴承研究所有限公司,洛阳 471039;4.高性能轴承数字化设计国家国际科技合作基地,洛阳 471039;5.河南省高性能轴承技术重点实验室,洛阳 471039)
0 引言
角接触球轴承具有良好的承载性能,且旋转精度高,广泛应用于精密机械领域,如航空发动机、高精度机床和精密磁盘等。轴承旋转精度对机械运行精度有重要影响,轴承各元件的几何误差又会对轴承的旋转精度产生决定性影响[1-3]。因此,研究轴承元件几何误差与轴承旋转精度的关系,对高精度轴承的研发有重要意义。
国内外学者以滚子轴承和球轴承为研究对象,分析轴承元件几何误差对轴承旋转精度的影响,取得了大量研究成果。余永健等[4-7]根据圆柱滚子轴承的几何和运动关系,分别建立了轴承内圈、外圈径向跳动数学模型,分析了内、外圈滚道圆度误差幅值、阶次、径向游隙和滚子个数对轴承旋转精度的影响;进一步研究了滚子误差和内外圈误差耦合作用对轴承旋转精度的影响。李传顺、吴柏华等[8-9]分别建立了深沟球轴承回转精度模型,吴柏华等[9]研究了轴承元件误差对轴承回转精度的影响。留剑等[10]通过建立角接触球轴承五自由度拟静力学模型,分析了内外圈沟道径向、轴向波纹度和钢球波纹度对轴承非重复性跳动的影响。NOGUCHI等[11-12]建立了角接触球轴承非重复性跳动数学模型,通过理论和试验分析了球轴承内外圈沟道几何误差、钢球直径误差和钢球个数对轴承非重复性跳动(NRRO)的影响。
纵观已有文献,发现关于角接触球轴承外圈几何误差对轴承旋转精度影响的研究目前相对不足。本文以角接触球轴承为研究对象,只考虑外圈沟道圆度误差,建立了外圈旋转精度数值仿真模型,分析了外圈沟道圆度误差阶次、圆度误差幅值、钢球个数和径向游隙对轴承旋转精度的影响,并验证了模型的准确性。
1 外圈旋转精度数值仿真模型
本文建立的轴承外圈径向、轴向跳动数值仿真模型假设条件为:①轴承内圈静止,外圈转动,钢球与内、外圈沟道不发生相对滑动,外圈与钢球稳定接触后不发生倾斜;②只考虑外圈沟道圆度误差对旋转精度的影响,不考虑轴承内部弹流润滑条件;③只考虑轴承元件间的几何和运动关系,钢球在内、外圈沟道之间均匀分布。
轴承内圈静止,外圈每次转动的角度为定值,外圈沟道轮廓曲线方程随着旋转角度的变化而变化,钢球公转到新的位置,然后沿着法线方向移动,直到与内圈沟道接触;外圈从初始位置朝钢球方向按设定步长平移,每一个位置都判断外圈沟道和钢球的接触情况,找出外圈处于稳定接触状态的位置,再通过轴承最优稳定接触状态判据找到最优外圈位置,即可求得外圈最优旋转中心坐标;外圈旋转一周,求出每个角度下外圈最优旋转中心坐标,找出所有坐标中Y坐标和Z坐标的最大值、最小值,它们的差值就是轴承外圈的径向跳动和轴向跳动。
1.1 轴承三维坐标系的建立
为了表示角接触球轴承钢球与内、外圈沟道接触的几何关系,本文建立了三维坐标系,如图1所示。

图1 角接触球轴承三维坐标系 图2 轴承轴向平面几何关系
钢球与内、外圈沟道理想接触时,接触点法线相交于轴线上同一点,即负荷中心T。以T为原心建立坐标系,其中,Z轴与轴承轴线重合,Y轴竖直向上,X轴垂直于YOZ平面。在轴承轴向平面内,钢球与内、外圈沟道的理想接触点分别是a和b,接触角为α,外圈沟道上理想接触点为c,如图2所示。
1.2 外圈沟道轮廓曲线方程
角接触球轴承外圈沟道每点的圆度误差均沿各自法线方向,用傅里叶级数表示外圈沟道圆度误差,外圈沟道圆度误差方程为:
(1)
式中,ΔS(θ1)为外圈沟道圆度误差;θ1为外圈沟道上的点在径向平面的位置角;m为圆度误差阶次;Am为圆度误差幅值,由式(2)计算;φ为初始相位角,由式(3)计算。
(2)
φ=arctan(bm/am)
(3)
式中,am、bm分别为第m阶谐波分量的正弦项系数和余弦项系数。
轴承外圈沟道轮廓曲线由外圈沟道理想圆和圆度误差相加而成。求解外圈沟道轮廓曲线方程时,首先在轴承轴向平面建立局部坐标系Y1OZ1,如图3所示。钢球与内圈沟道没有误差,接触角为理想接触角,外圈在初始位置,此时内、外圈旋转中心坐标的Y1值相等。根据轴承的几何关系,求出外沟道曲率中心oe在Y1OZ1平面的坐标。
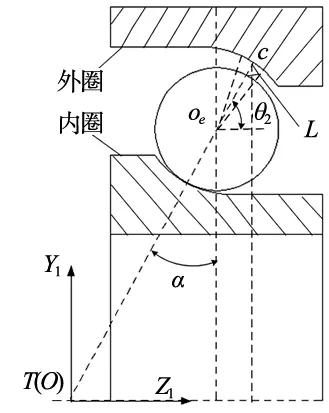
图3 外圈沟道曲线方程求解示意图
(4)
式中,de为外沟道沟底直径;Re为外沟道曲率半径;di为内沟道沟底直径;Ri为内沟道曲率半径;α为轴承理想接触角。
外圈沟道上点c到外沟道曲率中心oe的距离与水平方向的夹角为θ2,点c在Y1OZ1平面的坐标为:
(5)
点c到轴承轴线的距离为Y1c,给出该点在径向平面的位置角θ1,即可求出点c在三维坐标系中的X、Y坐标值,如图4所示。所以,外圈沟道轮廓曲线方程可以表示为:

图4 轴承径向平面几何关系
(6)
考虑圆度误差后,外圈沟道与钢球的接触点可能不在同一条轮廓曲线上,仿真计算时给定多条轮廓曲线,如图5所示。令θ2在理想角度附近按设定步长变化,可以得到外圈沟道上多条轮廓曲线,这些轮廓曲线的圆度误差具有相同的圆度误差阶次和初始相位。
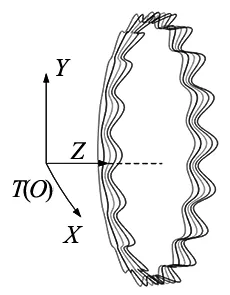
图5 外圈沟道轮廓曲线
1.3 计算外圈最优旋转中心坐标
外圈沟道旋转某一角度后,从初始位置按设定步长向钢球方向平移,每移动一个位置,判断外圈沟道和钢球的接触情况。
首先计算钢球球心坐标,钢球随着外圈旋转公转至新的位置,球心X、Y坐标值变化;钢球与内圈沟道理想接触,在轴线方向不移动,球心Z坐标值不变。在Y1OZ1平面内,第j个钢球球心坐标为:
(7)
式中,Dw为钢球直径。
钢球球心到轴承轴线的距离为Y1Oj,计算出球心在径向平面的位置角βj,即可求出球心在三维坐标系中的X、Y坐标值,如图6所示。
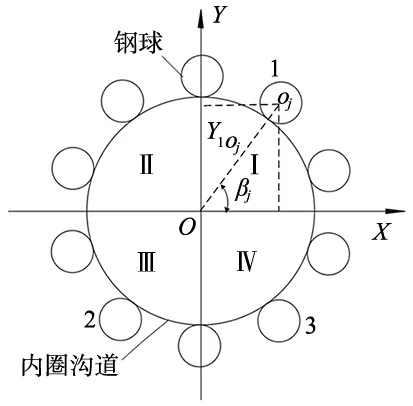
图6 钢球在径向平面的分布
第j个钢球的三维坐标为:
(8)
其次,计算外圈沟道在每个平移步长下的轮廓曲线方程,外圈在X、Y、Z方向发生位移,曲线方程为:
(9)
考虑圆度误差后,外圈沟道与钢球的实际接触点可能会发生变化。在外圈沟道上选取多个点,选取方法以理想接触点为中心作网格划分,令θ1和θ2在各自理想角度两侧按设定步长变化。依次计算选取的每个点到钢球表面的距离,判断外圈沟道和钢球是否接触。
设外圈沟道上的点到钢球表面的距离为L。
(10)
计算外圈沟道上选取的每个点到钢球表面的距离,求出一系列L值,比较得出其中的最小值Lmin。设ε为允许干涉误差,当Lmin<-ε时,外圈沟道与钢球干涉;当|Lmin|<ε时,外圈沟道与钢球接触;当Lmin>ε时,外圈沟道与钢球分离。
依次计算外圈沟道与每个钢球的接触情况,判断外圈是否处于稳定接触状态。外圈处于稳定接触状态的条件为:不能与钢球发生干涉;有效接触钢球个数在3个及以上;有效接触钢球在径向平面内至少在3个象限内分布。判断有效接触钢球象限分布的方法如图6所示,有效接触的钢球为1、2和3,这3个钢球分布在3个象限,此时外圈沟道处于稳定接触状态。
满足稳定接触状态的外圈位置可能有多个,当存在多个位置时,通过外圈最优稳定接触状态判据找到最优外圈位置。即比较外圈稳定接触位置中,每个位置有效接触钢球个数,选择接触钢球个数最多的位置;如果有效接触钢球个数同为最多,取外圈位移最小的位置为最优外圈位置。最优外圈位置的旋转中心坐标即为外圈最优旋转中心坐标。
2 数值仿真模型理论验证
为了验证仿真模型的准确性,以圆度误差阶次为18和36进行理论计算,求出外圈每一转动角度下的轴向跳动值,选用的角接触球轴承几何参数如表1所示。圆度误差阶次为18和36时,外圈沿Z轴移动即可与所有钢球接触,所以外圈只有轴向跳动,没有径向跳动。

表1 轴承几何参数
首先,计算外圈轴向跳动值历程中的周期和最大值点,外圈沟道轮廓曲线的初始相位角设为0。在初始位置,外圈沿Z轴移动,外圈沟道的波峰与钢球1接触,此时外圈移动量最大,在该角度下外圈轴向跳动值最大,如图7所示。
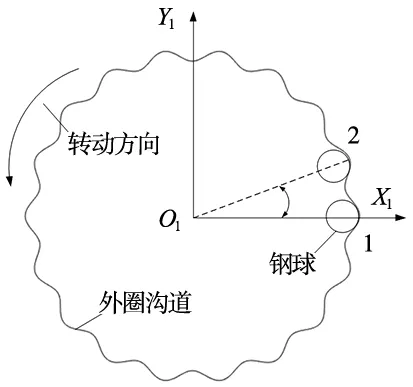
图7 外圈沟道与钢球的运动关系
外圈转动时,钢球公转速度为[13]:
(11)
式中,Vm为钢球公转速度;Ve为外圈公转速度;dm为轴承节圆直径,求得dm=(di+de)÷2。
单位时间内,外圈转动角度γe等于公转速度Ve,钢球转动角度γm等于公转速度Vm,设外圈公转速度Ve为1。外圈转动时,当外圈沟道的波峰再次与钢球接触时,外圈轴向跳动值完成一个周期,外圈转动的角度为γ,由式(12)计算。外圈转动一圈,轴向跳动值历程周期T由式(13)计算。
(12)
T=360/γ
(13)
圆度误差阶次为18时,外圈轴向跳动值历程近似有7.8个周期,且外圈沟道波峰与钢球接触8次,外圈轴向跳动值最大值出现8次。圆度误差阶次为36时,外圈轴向跳动值历程近似有15.7个周期,且外圈沟道波峰与钢球接触16次,外圈轴向跳动值最大值出现16次。
然后进行理论验证公式推导,外圈只沿Z轴平移,外圈沟道轮廓曲线方程为:
(14)
当外圈沟道与钢球接触时,外圈沟道上的点到钢球球心的距离等于钢球半径,可得表达式:
(15)
由式(14)和式(15)联立可以求得:
(16)
分别求出外圈沟道每个点与钢球接触时在Z轴的移动量Δz,找出最小移动量Δzmin,当外圈移动Δzmin时,外圈沟道与钢球接触。外圈旋转一周,求出每一个角度外圈轴向跳动值。
如图8所示可知,外圈转动一周,在初始位置外圈轴向跳动值最大,最大值点有8个,外圈轴向跳动值历程有7个整周期。如图9所示可知,外圈转动一周,在初始位置外圈轴向跳动值最大,最大值点有16个,外圈轴向跳动值历程有15个整周期。如图8和图9所示,说明仿真计算与理论计算历程一致,并且每个转动角度下,理论计算和仿真计算的轴向跳动值相差很小。

图8 m=18时理论与仿真结果对比

图9 m=36时理论与仿真结果对比
由表2结果可知,仿真计算的轴向跳动相较理论计算值误差小于3%,误差范围合理。综上所述,本文提出的轴承外圈径向、轴向跳动预测模型合理准确,可以用来预测角接触球轴承的旋转精度。

表2 结果对比
3 数值仿真计算结果及分析
根据上文中建立的外圈旋转精度数值仿真模型,编写相应程序,分析外圈沟道圆度误差阶次、圆度误差幅值、钢球个数和径向游隙与外圈旋转精度的传递规律。
3.1 圆度误差阶次对轴承径向、轴向跳动的影响
图10为钢球数Z为18时,外圈沟道圆度误差阶次对外圈旋转精度的影响;图11为钢球数Z为17时,外圈沟道圆度误差阶次对外圈旋转精度的影响。其中,圆度误差幅值为0.002 mm,径向游隙为0.04 mm。由图10和图11可以看出,随着外圈沟道圆度误差阶次的变化,外圈的径向跳动和轴向跳动呈现周期性变化规律,周期为钢球个数。
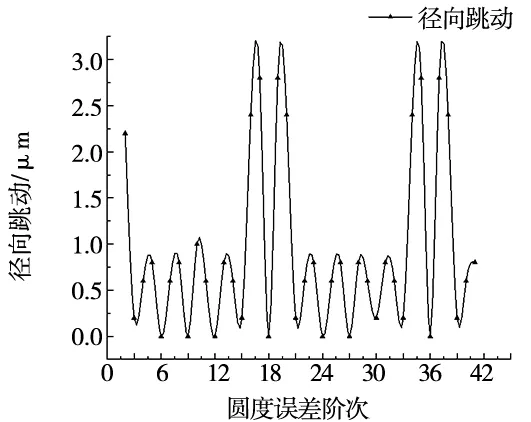
(a)径向跳动
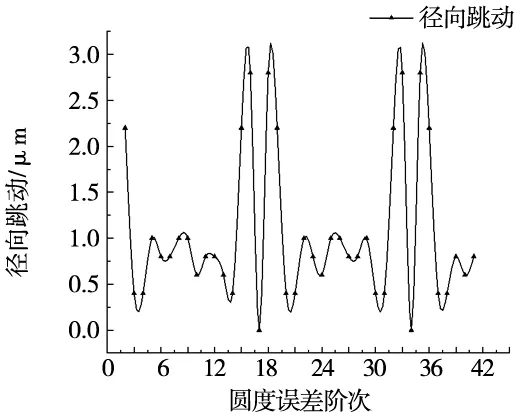
(a)径向跳动
对于径向跳动,当圆度误差阶次为(nZ±1,nZ±2)(n=1,2)时,外圈径向跳动明显增大。对于轴向跳动,当圆度误差阶次为钢球数的整数倍时,外圈轴向跳动取得最大值;当圆度误差阶次和钢球数有公约数时,外圈轴向跳动取得极大值,且公约数越大,外圈轴向跳动越大。
综合考虑外圈沟道圆度误差阶次对外圈径向、轴向跳动的共同影响,当圆度误差阶次分布在合理区间内,外圈径向跳动和轴向跳动都取得较小值。这说明通过谐波控制理论,使阶次分布在合理区间内,可以有效提高轴承旋转精度。
3.2 圆度误差幅值对轴承径向、轴向跳动的影响
图12为外圈沟道圆度误差幅值对外圈径向、轴向跳动的影响。其中,钢球个数为18个,圆度误差阶次为8阶,径向游隙为0.04 mm。从图中可以看出,轴承外圈径向跳动和轴向跳动随着误差幅值的增大而增大;轴向跳动呈近似线性增长,径向跳动的增长幅度相比轴向跳动更大。这说明外圈沟道圆度误差幅值对轴承外圈旋转精度有很大影响,这是因为误差幅值增大使外圈沟道波峰和波谷的距离增大,外圈的位移随之增大,轴承跳动明显。因此,可以通过减小轴承套圈圆度误差幅值提高轴承旋转精度。
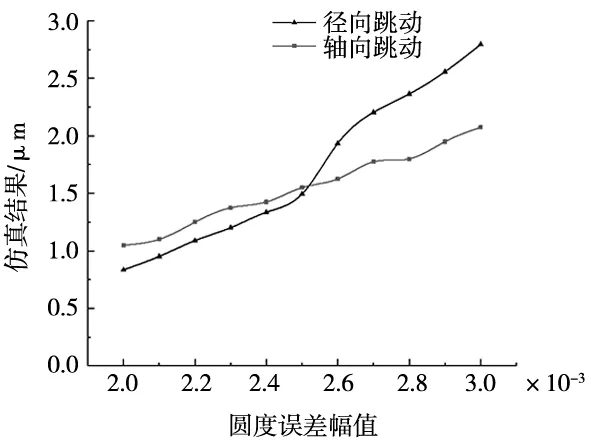
图12 圆度误差幅值对外圈旋转精度的影响
3.3 钢球个数对轴承径向、轴向跳动的影响
图13为钢球个数对轴承外圈径向、轴向跳动的影响。其中,圆度误差幅值为0.002 mm,圆度误差阶次为2阶,径向游隙为0.04 mm。从图中可以看出,随着钢球数量的增加,外圈径向、轴向跳动呈减小趋势。这是因为增加钢球个数可以减小钢球间的跨距,外圈沟道在轴向、径向方向移动时与钢球接触的几率增大,使外圈在轴向、径向方向的位移减小,所以外圈轴向、径向跳动减小。因此,在角接触球轴承设计时,可以通过适当增加钢球个数,以提高轴承的旋转精度。
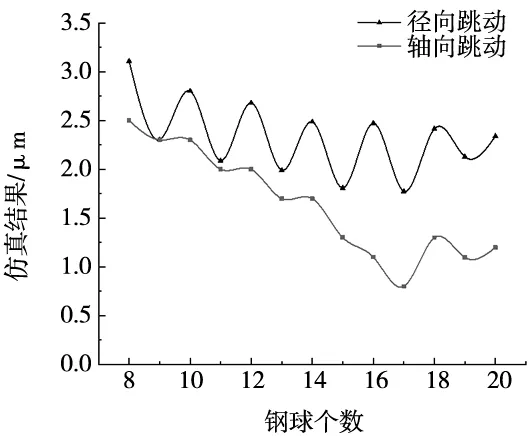
图13 钢球个数对外圈旋转精度的影响
4 结论
(1)角接触球轴承外圈径向、轴向跳动随着外圈沟道圆度误差阶次的变化呈周期性变化,周期为钢球个数。
(2)当圆度误差阶次与钢球个数相差1时,外圈径向跳动取得最大值;当圆度误差阶次和钢球数有公约数时,外圈轴向跳动取得极大值,且公约数越大,外圈轴向跳动越大,圆度误差阶次为钢球数整数倍时,轴向跳动取得最大值。
(3)通过谐波控制理论,抑制外圈沟道上特定的圆度误差阶次,可以有效提高轴承旋转精度。
