基于非线性破坏准则的地下连续墙槽壁稳定性能耗分析方法研究
2022-03-30黄阜王子钦罗跃龙周惠聪
黄阜,王子钦,罗跃龙,周惠聪
(长沙理工大学土木工程学院,湖南 长沙 410114)
基坑工程是明挖地下结构或者高层建筑基础不可或缺的一部分。随着我国城市化进程的加速,各大城市的基础设施建设正在如火如荼地进行,基坑也随着这些基础设施的建设出现在各种工程中。作为基坑围护结构的一种重要形式,地下连续墙因其适用性强、整体性能好、施工效率高等优点,在基坑工程中得到了广泛应用。地连墙在成槽施工过程中虽然有泥浆护壁这一工艺对槽壁的稳定性进行保护,但是如果地层的地质条件比较差,泥浆压力不足以抵挡槽壁两侧的土压力时,容易发生槽壁坍塌失稳现象(也就是工程中俗称的塌孔)。一旦地连墙槽壁发生塌孔,坍塌的土体会混入浇筑的地连墙中,从而导致地连墙的整体性下降,强度达不到设计要求,进而影响基坑的整体安全。地连墙的塌孔往往发生在槽壁深处,施工人员很难依靠肉眼或者常见探测设备观测。因此,工程界对于地连墙塌孔的破坏特征和坍塌范围的研究还不够深入。另一方面,已有的针对地连墙槽壁稳定性研究大都是基于线性破坏准则开展的[1-5]。而大量研究和工程实践表明,岩土介质服从非线性破坏准则,线性破坏准则难以反映岩土体的非线性破坏特征[6-8]。因此,有必要在考虑岩土体非线性破坏特性的情况下,对地连墙槽壁失稳破坏的发生机理和破坏模式开展研究。目前,国内外很多学者已经对地连墙槽壁的稳定性问题开展了研究工作。FOX[9]通过建立楔形体破坏机制,提出了地连墙槽壁安全系数的计算方法。夏元友等[10]根据极限平衡理论,以二维楔形块体为研究对象,提出了基于水平条分法的地下连续墙泥浆护壁稳定性分析方法。HAN 等[11]基于极限分析方法,利用对数螺旋线构建地连墙槽壁失稳破坏机制,推导得到了槽壁稳定性安全系数上限解。ZHANG 等[12]基于极限平衡理论和变分法,提出了考虑孔隙水压力作用的地连墙槽壁稳定性分析方法。上述针对地连墙槽壁稳定性的研究,大多是利用预先假设的形状(楔形体、对数螺旋线等)来构建地连墙槽壁的理论计算模型。但在实际工程中,地连墙槽壁土体的坍塌失稳具有偶然性,利用预先假设的失稳破坏形状对槽壁稳定性进行分析,难以反映槽壁土体的真实破坏特征。针对目前槽壁稳定性研究中存在的问题,本文利用空间离散技术,构建了地连墙成槽施工过程中槽壁的二维离散型破坏机制。基于Mohr-Coulomb(M-C)非线性破坏准则和极限分析上限定理,推导出地连墙槽壁安全系数的目标函数,然后利用非线性规划程序,计算得到地连墙槽壁安全系数的上限解,并探讨各参数变化对安全系数的影响。研究成果可以为地连墙成槽施工过程中槽壁稳定性研究提供参考。
1 Mohr-Coulomb非线性破坏准则
BIENIAWSKI[13]提出,在M-C 非线性破坏准则中,屈服面上的最大主应力σ1和最小主应力σ3呈非线性关系,该非线性关系可以由式(1)表示:
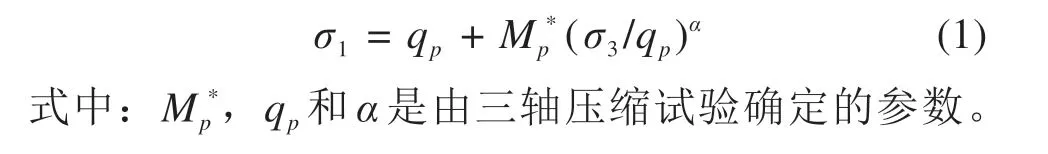

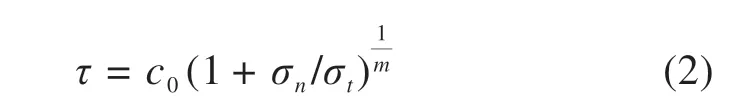
其中:c0为初始黏聚力;σt为轴向拉应力;m为非线性参数。当m= 1 时,式(2)转化为M-C 线性破坏准则;当m< 1 时,不符合塑性力学的加载面外凸性原则,不予以讨论;当m> 1时,式(2)为非线性破坏准则,切应力和主应力之间的非线性关系可以表示为图1所示的曲线。
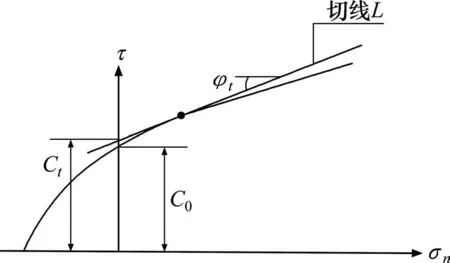
图1 非线性破坏准则的切线Fig.1 Tangent line of nonlinear failure criterion
由于结构的极限荷载不会因材料的屈服强度提高而降低,因此可采用超过真实屈服强度的材料强度计算非线性破坏准则下的真实屈服强度。本文基于YANG 等[14−16]提出的“切线法”,将非线性破坏准则引入上限分析中。即通过图1切线上随σn增大而增大的各点所对应的材料强度,获得各机动容许速度场对应真实极限荷载的上限值。从图1中可以看出,非线性破坏准则中的黏聚力c和摩擦角φ随σn的变化而变化,因此可以采用瞬时黏聚力ct和瞬时摩擦角φt作为任意一条切线对应的抗剪强度指标值。因此,图1中任意一条切线方程可以表示为:
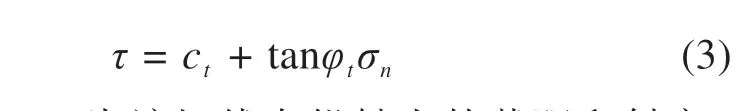
式中:ct和tanφt为该切线在纵轴上的截距和斜率。ct和tanφt的值可以由以下2个公式计算得到:
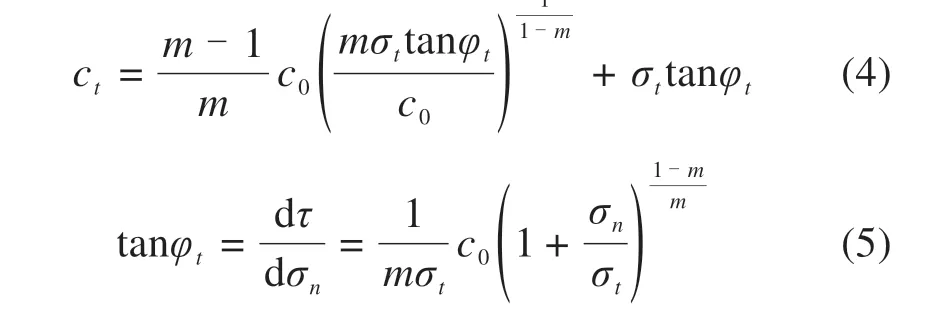
进行上限分析时,根据优化理论,将tanφt视为变量,利用基于Nelder-Mead 单纯形法的优化计算程序,搜索得到无约束条件下的tanφt最优值。
2 基于空间离散技术的地下连续墙槽壁失稳破坏机制
由于在地连墙成槽施工过程中,对土体原始应力场产生了扰动,使得原本处于稳定状态的土体发生了应力重分布。虽在沟槽内注入泥浆以防止槽壁坍塌,但当泥浆支护作用小于静止土压力时,槽壁有可能在局部区域发生垮塌。目前大多数针对槽壁稳定性的研究都采用由假定的几何形状(楔形体、对数螺旋线等)构成的破坏面进行分析,但在实际工程中,地连墙槽壁不一定按照假定的几何形状发生破坏。MOLLON 等[17-19]针对非均质土体中盾构隧道开挖面的稳定性问题,提出了一种由空间离散技术构成的开挖面破坏机制。该破坏机制利用离散法逐点生成速度间断线,再由速度间断线组成“牛角型”破坏面。该方法生成的破坏机制与传统的由几何形状构成的破坏机制相比,能够模拟复杂地层中隧道开挖面的破坏情况,计算结果精确性更高。因此,本文将MOL‐LON 提出的空间离散技术引入地连墙槽壁稳定性分析中,构建了地连墙槽壁坍塌失稳的二维离散型破坏机制。
基于空间离散技术构建的地连墙槽壁失稳破坏机制如图2 所示,AB为地面,BC为槽壁,H为地连墙开槽深度,Hs为护壁泥浆面到槽底的高度。由空间离散技术生成的速度间断线AC,从地连墙底部延伸到地表,构成了刚性破坏体ABC。假设破坏体ABC以角速度ω绕旋转中心O点顺时针转动。
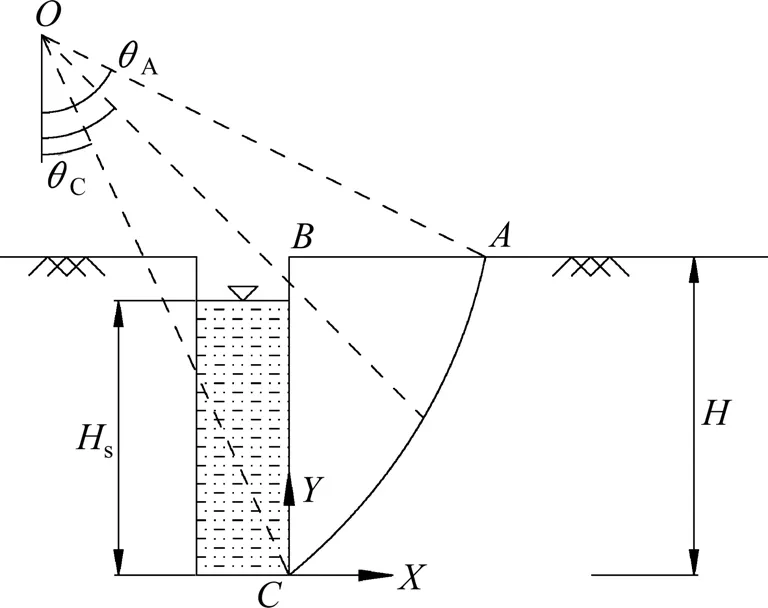
图2 地下连续墙槽壁整体模型Fig.2 Overall model of slurry trench
地连墙槽壁的速度间断线AC生成示意图如图3所示。该速度间断线的生成方法MOLLON 等[17−21]已经在论文中进行了详细阐述。
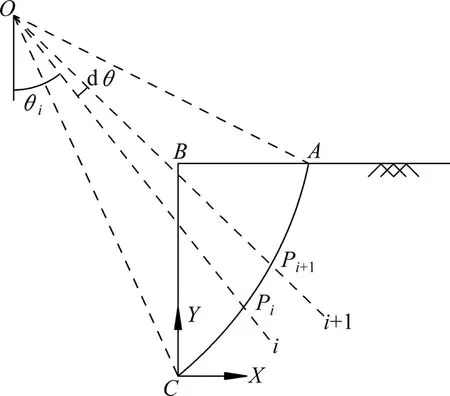
图3 地下连续墙槽壁破坏机构生成过程Fig.3 Generation process of slurry trenches failuremechanism
dθ为离散机构的控制参数之一,本文取0.1°。旋转中心O点的坐标为(x0,y0),B点的坐标为(0,H),其中O点的坐标可以用与O点的距离以及角度参数来表示:

其中:
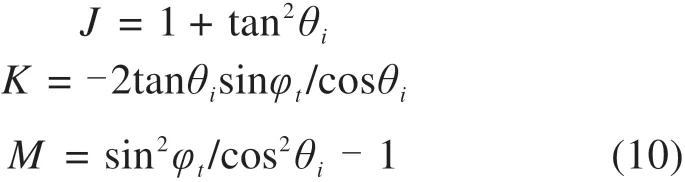
由于法向量ni必须指向速度间断面外侧,故有:

滑动面的生成是从C点开始,依次生成P1,P2,P3等,直到yj>H或yj+1=H时才停止。若yj>H,则可以利用线性插值,使得yj=H。
3 基于极限分析理论的地连墙槽壁破坏机制能耗计算
3.1 重力功率的计算
本文构建的滑动面由空间离散技术生成,因此,土体的重力功率需要先计算滑动面上离散单元体PiPi+1B的重力功率,再对滑动面上所有离散单元体的重力功率进行积分。其中离散单元体划分如图4所示。
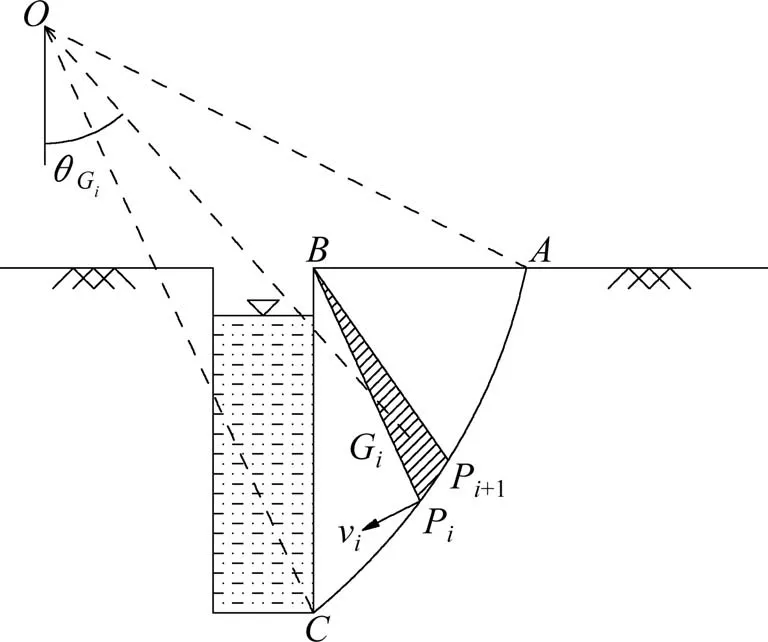
图4 破坏体的单元计算示意图Fig.4 Calculation schematic of the unitary destructive body
土体重力做功的计算公式为:
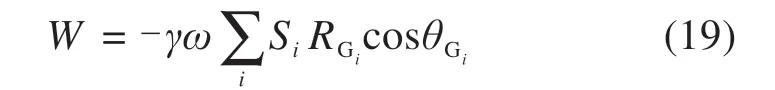
式中:Si为三角形离散单元块体BPiPi+1的面积,Gi为三角形BPiPi+1的重心,其坐标为:

最后,将滑动面上所有单元体的重力功率累加,得到塌落体ABC的总重力功率。
3.2 内能耗散功率的计算
由于假定破坏体ABC是刚性体,在绕O点发生转动时刚性体的体积不发生任何变化,因此内能耗散都在速度间断线AC上产生。计算速度间断线AC上的内能耗散功率时,首先需要先计算速度间断线AC上任意小段PiPi+1的内能耗散功率,然后将该段的内能耗散功率沿速度间断线AC进行积分,得到总内能耗散功率:

式中:Li为线段PiPi+1的长度;Ri为O点到PiPi+1段中点的距离。
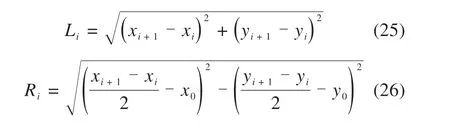
3.3 泥浆支护力功率的计算
为了简化计算,将泥浆压力假设为线性递增的均布力水平作用在槽壁两侧,如图5所示。泥浆支护力功率可以用离散单元体与泥浆的相对速度v'i和泥浆压力点乘的积分来表示。图5中Ti为相对速度v'i的位置,即PiPi+1段中点到O点的连线与BC段的交点,OTi长度可由正弦定理得到:

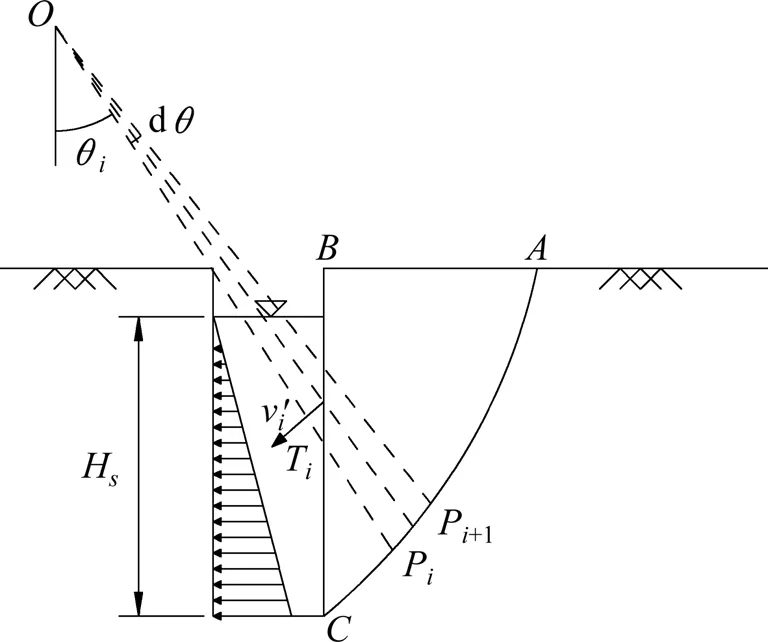
图5 泥浆功率计算示意图Fig.5 Slurry power calculation diagram
因此,槽壁上Ti点的泥浆与单元滑动体的相对速度大小为:

3.4 地连墙槽壁安全系数上限解
根据极限分析上限定理,在土工结构的机动速度场中,其外力功率小于或等于内能耗散功率时,该结构才能保持稳定。根据SAADA 等[22]给出的边坡安全系数定义,安全系数等于机动速度场中内能耗散功率与总外力功率的比值:

式中:D为机动速度场内能耗散功率;W为机动速度场中的总外力功率。参考SAADA 等[22]提出的安全系数定义,将计算得到的内能耗散功率与总外力功率代入式(30),得到了地连墙槽壁安全系数的上限目标函数。由于该目标函数包含多个变量,且变量之间为非线性关系,难以通过解析方法解得安全系数最优值。因此,本文使用优化程序来搜索目标函数的最小值,通过编制优化程序得到无约束条件下地连墙槽壁安全系数的最优上限解。
4 对比计算
为了验证本文采用极限分析理论计算的地连墙槽壁安全系数上限解的有效性,利用有限差分软件FLAC3D构建了地连墙成槽施工的三维模型。在此基础上,结合强度折减法,计算得到了槽壁在极限状态下的安全系数数值解,并与上限解进行对比分析。
本文构建的地连墙数值模型尺寸如下:地连墙开槽深度H=20 m,泥浆高度Hs= 19 m,模型上边界取至地面,下边界取至地连墙底部以下20 m,地连墙宽度取2 m。成槽施工过程中,通过在槽壁两侧施加线性递增的水平力,模拟护壁泥浆对槽壁两侧土体的支护作用。由于本模型是一个左右对称结构,数值模型只构建了右半部分以提高计算效率,数值模型如图6 所示。在成槽施工过程中,调用M-C 本构模型,利用强度折减法对土体黏聚力和摩擦角进行折减,当槽壁达到临界状态时,可得到极限平衡状态下的折减系数,即所求的地连墙槽壁安全系数。由于非线性参数m= 1时,非线性M-C 破坏准则可转化为线性M-C 破坏准则,因此可将基于上限理论计算得到的非线性参数m= 1 情况下的槽壁安全系数理论解与采用线性M-C 破坏准则的安全系数数值解进行对比。当土体重度γ=18 kN/m3,泥浆重度γs=10.8 kN/m3,内摩擦角φ= 10∘,黏聚力c=10~30 kPa,非线性参数m= 1 时,计算得到的安全系数上限解与数值解对比如表1 所示。从表1 中可以看出,安全系数上限解与数值解都随着黏聚力c的增大而增大,并且两者的最大差值不超过11%。图7 为极限状态下,数值模拟得到的地连墙槽壁剪切应变增量(SSI)云图和基于上限理论计算得到的槽壁土体滑移破坏面对比图。从图7中可以看出,槽壁土体形成了由剪切应变带构成的破坏面,且该破坏面与上限计算得到的破坏面形状相近,破坏范围也基本一致。由此可见,本文采用极限分析理论计算得到的地连墙槽壁安全系数是有效的。
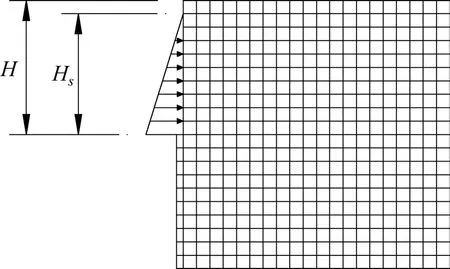
图6 地下连续墙成槽施工数值模型Fig.6 Numerical model for underground diaphragm wall trenching construction
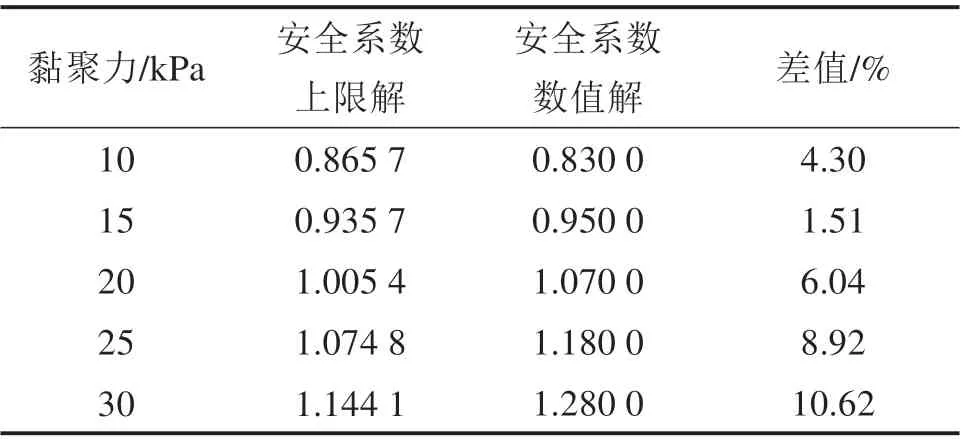
表1 槽壁安全系数上限解与数值解对比Table 1 Comparison of the upper limit solution and numerical solution of the safety factor for the slurry trench
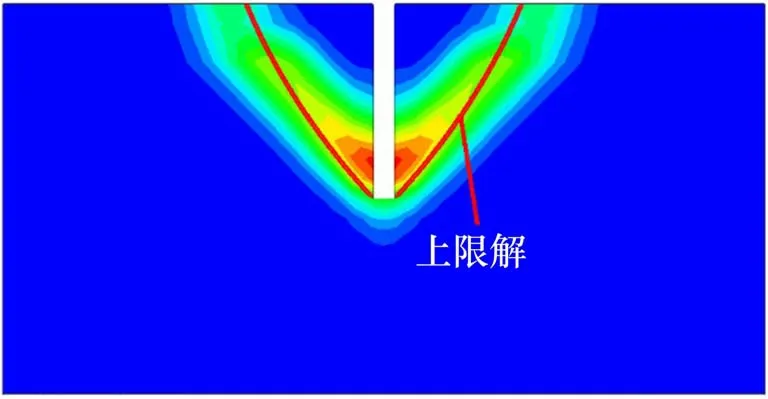
图7 槽壁极限状态下失稳破坏滑移面的上限解和数值解对比Fig.7 Comparison of upper limit solutions and numerical solutions of slip surface for slurry trench in the limit state
5 影响参数分析
为了分析各参数对于槽壁安全系数的影响,根据上限计算结果,绘制了地连墙开槽深度H=12~20 m,土体重度γ=18~26 kN/m3,轴向拉应力σt=100~180 kPa,泥浆重度为γs=12~16 kN/m3,初始黏聚力c0=10~30 kPa,非线性参数m=1.2~1.8 时,泥浆高度与地连墙开槽深度比值Hs/H=0.75~0.95,槽壁安全系数随单一参数变化的曲线图,如图8所示。从图8(a),8(c)和8(e)可以看出,在其他影响因素不变的情况下,安全系数随着初始黏聚力c0,泥浆高度与地连墙开槽深度比值Hs/H以及泥浆重度γs的增大而增大。此外,从图8(b),8(d)和8(f)中可以看出,地连墙槽壁安全系数随着轴向拉应力σt,地连墙开槽深度H和土体重度γ的增大而减小。
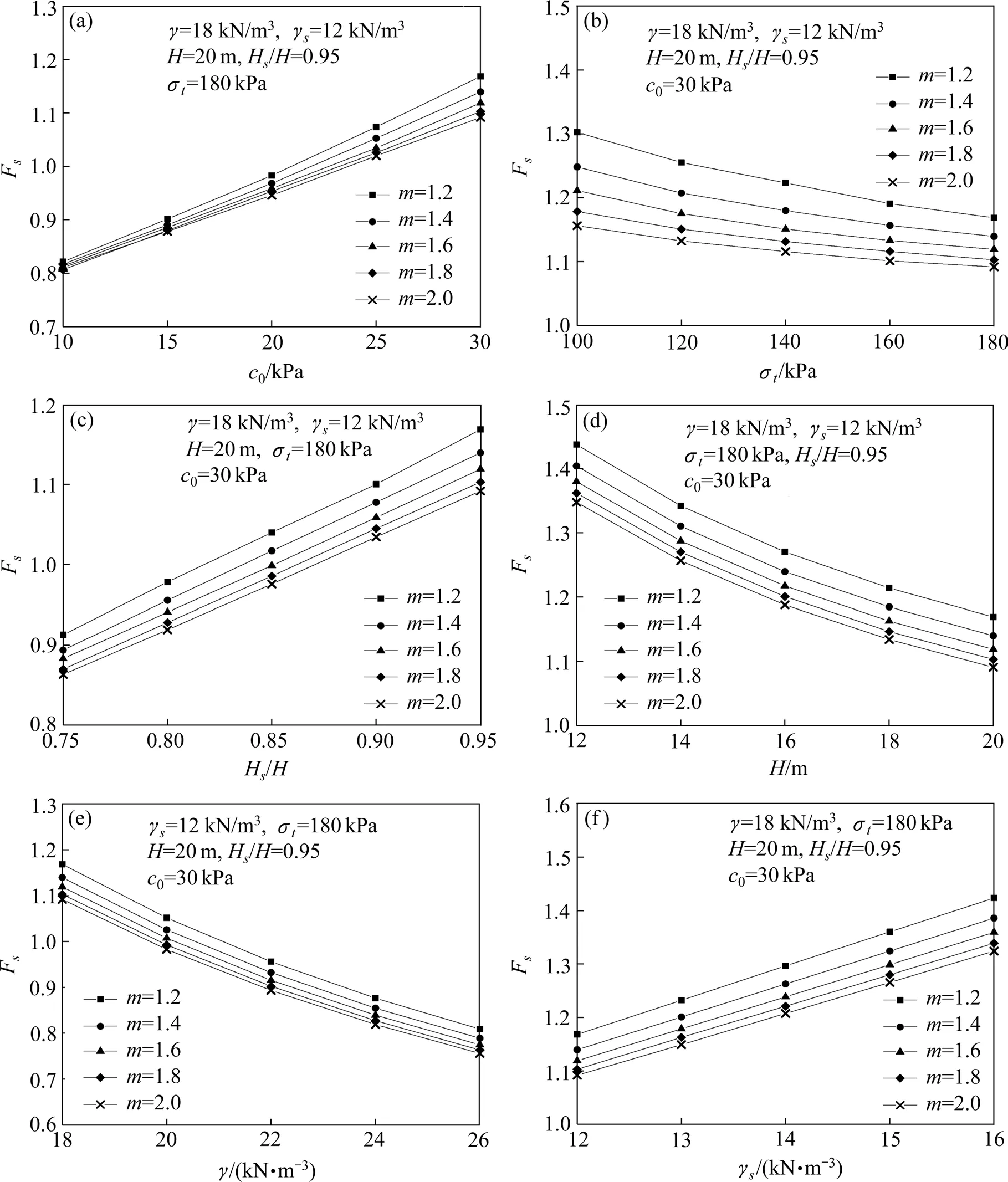
图8 不同参数对地连墙槽壁安全系数的影响Fig.8 Influence of different parameters on safety factor of slurry trench
将优化计算得到的地连墙槽壁速度间断线上各点的坐标导入CAD,可以绘制出地连墙槽壁在极限状态下的坍塌破坏面。图9 和图10 分别为当地连墙开槽深度H=20 m,泥浆高度Hs=19 m,土体重度γ=18 kN/m3,泥浆重度γs=12 kN/m3,轴向拉应力σt=180 kPa,初始黏聚力c0=10~40 kPa,非线性参数m=1.2~1.8 时,槽壁土体破坏面的形状。从图9 和图10 可以看出,当其他参数不变时,槽壁塌孔的破坏范围随着初始黏聚力c0的增加而缩小,随着非线性参数m的增大而增大。
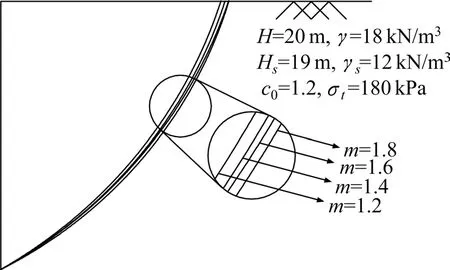
图9 不同初始黏聚力对地连墙槽壁破坏面的影响Fig.9 Influence of different initial cohesion on the failure surface of the slurry trench
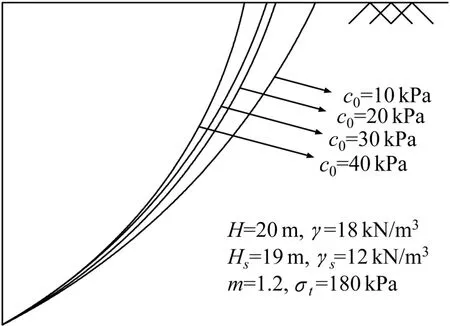
图10 不同非线性参数对地连墙槽壁破坏面的影响Fig.10 Influence of different nonlinear coefficients on the failure surface of slurry trench
6 结论
1) 土体的非线性破坏特征对地连墙槽壁安全系数有较大影响。地连墙槽壁安全系数随着非线性参数m以及轴向拉应力σt的增大而减小,随着初始黏聚力c0的增大而增大。
2) 地连墙槽壁在极限状态下的破坏范围随着初始黏聚力c0的增加而减小,随着非线性参数m的增大而增大。在地连墙成槽施工过程中,有必要考虑土体的非线性破坏特征对极限状态下地连墙槽壁坍塌范围的影响。
3) 地连墙槽壁安全系数随着土体重度、地连墙开槽深度的增加而减小,随着泥浆高度与地连墙开槽深度的比值Hs/H以及泥浆重度γs的增大而增大。因此,提高护壁泥浆的稠度是提升地连墙槽壁稳定性的有效方法之一。
