基于Moran′s I的林分空间结构量化指标自相关分析
2022-03-30卿东升彭进香李建军邓巧玲
卿东升,彭进香,李建军,邓巧玲,刘 帅
(1.中南林业科技大学,长沙 410000;2.湖南应用技术学院,湖南 常德 415000;3.南方林业生态应用技术国家工程实验室,长沙 410000)
森林是人类及其它动物、微生物赖以生存、不可或缺的环境基础,林分空间结构在相当大程度上主导着林分当前的健康状态和未来的发展方向[1]。惠刚盈等[2]、汤孟平等[3]在探讨林分空间结构关系问题时指出:林分空间结构是林分群落内物种的空间关系、林木的分布格局及其属性在空间上的排列方式,是林木空间分布格局、树种混交和树木大小的空间排列。林分空间结构决定了林分内物种在空间上的关系,影响林木之间的竞争,在一定程度上反映出林分的稳定性、发展的可能性和经营空间的大小[4]。
根据研究现状可知,当前大部分的研究均通过选取相应的林分空间结构量化指标(比如混交度、角尺度等等),并从林分整体的角度上构建了一个林分空间结构综合评价模型,以此来反映整体林分在空间上的分布情况[5-9]。然而,从林木的空间结构单元上看,除了有相应的空间结构量化指标外,林分中林木的空间结构量化指标是否存在空间自相关性并不清楚。比如,对于胸径大小比值较大的对象木,其相邻木所对应的胸径大小比值是否大概率会大,对象木与相邻木胸径大小比的值是正相关还是负相关、其在逻辑上是聚集还是离散等问题并没有相关文献研究详细报道。
Moran′s I是由澳大利亚统计学家帕克·莫兰在1950年提出,用来计算样本在空间中是否存在自相关的重要指标,它可以判断研究对象与邻居在空间上是否存在自相关性的情况,目前,已经被成功应用到很多领域中[10-13]。本文结合林分空间关系量化指标方案及全局Moran′s I的数学原理,选取了混交度、开阔比数、胸径大小比数及竞争指数为林分空间结构量化指标,在此基础之上构建了林分空间关系自相关性评价方案,并以大围山、乌云界等研究区域中的25块样地为基础数据,从林分空间结构的角度上分析了该区域内对象林木与其相邻木在空间属性上的自相关性,以此说明对象林木与其相邻木在逻辑上是否存在聚集或者离散现象等问题,为林分空间经营管理提供参考。
1 研究区域及数据来源
在大围山自然保护区、龙虎山森林公园、青石岗林场、芦头林场及乌云界自然保护区中设置了25块大小为20m×20m的样地。大围山自然保护区位于湖南省浏阳市湘赣界,是连云山脉的腹地,东边属江西省宜春市下辖的铜鼓县,西北方为湖南浏阳市的东北部,地理位置为北纬28°21′~28°26′N,东经114°02~114°12′E,总面积7万余亩,大围山里面有鹅掌楸(Liriodendronchinense(Hemsl.)Sarg.)、方竹(Chimonobambusaquadrangularis(Fenzi)Makino)及银杏(GinkgobilobaL.)等珍贵植物;龙虎山森林公园位于湖南省益阳市沅江市新湾镇,赤山岛南端,其地理位置为北纬28°54′4″~28°54′56,东经112°17′2″~112°18′30″,公园占地500余亩,该地区属于大陆性季风湿润气候,雨水充沛,植物种类繁多,有部分地区保存最完整的原始次生林;青石冈林场位于湖南省株洲市炎陵县东南部,罗霄山脉中段和万洋山北段之西北坡、南岭山脉北麓,为南岭山地向湘中丘陵过渡的边缘地带,林场总经营面积37.625 8万亩,森林覆盖率达97.71%;芦头林场位于湖南省岳阳市平江县东南面,距县城50km,地处北纬28°31′7″~28°38′,东经113°51′52″~113°58′24″之间,现有林地面积5 040hm2,活立木蓄积276 842m3,森林覆盖率93.2%。乌云界自然保护区位于湖南省桃源县南部,地处雪峰山余脉的北坡,云贵高原向湘赣丘陵、湘西山地向洞庭湖平原过渡的典型地带,地处北纬28°29′~28°40′,东经111°06′~111°20′,占地面积33 818 hm2,其中森林面积27 610 hm2,森林植被覆盖率达92.5%。文中对所选样地中所有胸径大于5cm的林木进行测量,记录了树种的名称、胸径、树高等信息,研究区域主要树种及各样地林分调查情况如表1和表2所示。

表1 研究区域主要树种

表2 研究区域林木调查状况

(续表)
2 研究方法
2.1 林分空间结构量化指标
本文参考相关文献中的方法,选用的林分空间结构量化指标为混交度[14]、开阔比数[15]、胸径大小比数[16]及竞争指数[17-18]。
1)混交度
混交度用来描述不同林木之间的相互隔离程度,如式(1)所示:
(1)
式中:Mi表示对象林木i的混交度,当对象林木i与相邻木j为同种林木时,vij=0,否则vij=1,n是对象木的邻木株数。
2)开阔比数
开阔比数定义为空间结构单元中对象木i受相邻木遮蔽的程度,如式(2)所示:
(2)
式中:OPi表示对象木i的开阔比数,n为相邻木的株数,tij表示开阔比数取值变量,当对象木i与相邻木j的水平距离大于对象木i与相邻木j的树高都差时,tij=1,否则tij=0。
3)胸径大小比数
大小比数定义为胸径大于对象木i的相邻木数占所相邻木的比例,用公式(3)表示:
(3)
式中:Ui表示林分空间结构中林木i的胸径大小比数,n为相邻木的株数,i为对象木,j为相邻木,若对象木的胸径i比邻近树j小,kij=1,否则,kij=0。
4)竞争指数
竞争指数用来描述林分内林木之间的竞争关系,采用改进的Hegyi竞争指数描述树木竞争状况用公式(4)表示:
(4)
式中:CIi代表对象林木i的竞争指数,LD表示林分内空间结构单元中相邻木与对象木i之间距离的平均值,Lij为对象木i与竞争木j之间的距离,di对象木i的胸径,dj为相邻木的胸径,n为相邻木的株数。
5)单木综合评价指标
根据研究现状,林木空间结构的评价一般包含多个指标,林分空间结构评价问题实质上是一个多目标问题,文中借鉴相关文献中的方法[19-22],构建的单木综合评价指数如下:
(5)
2.2 基于Voronoi图的相邻木构建方法
如何量化林木空间单元是林分空间结构评价中的关键问题,文中根据Voronoi图原理及相关文献中的方法[23-24],对研究样地中的所有林木构建Voronoi图,把与对象木i的泰森多边形的边相邻的林木作为其相邻木,其与对象木i一起构成一个空间单元。为了消除边缘效应,文中根据样地实际大小,把距离样地边界0.5m的范围设定为缓冲区,规定该区域内的林木只能作为竞争林木,如图1所示。
2.3 基于Moran′s I的林分空间结构自相关性评价方案
2.3.1全局Moran′s I的基本原理
Moran′s I对于解决样本在空间中是否存在自相关时非常有效,基本的全局Moran′s I表示如式(6)~(7)所示[25-27]:
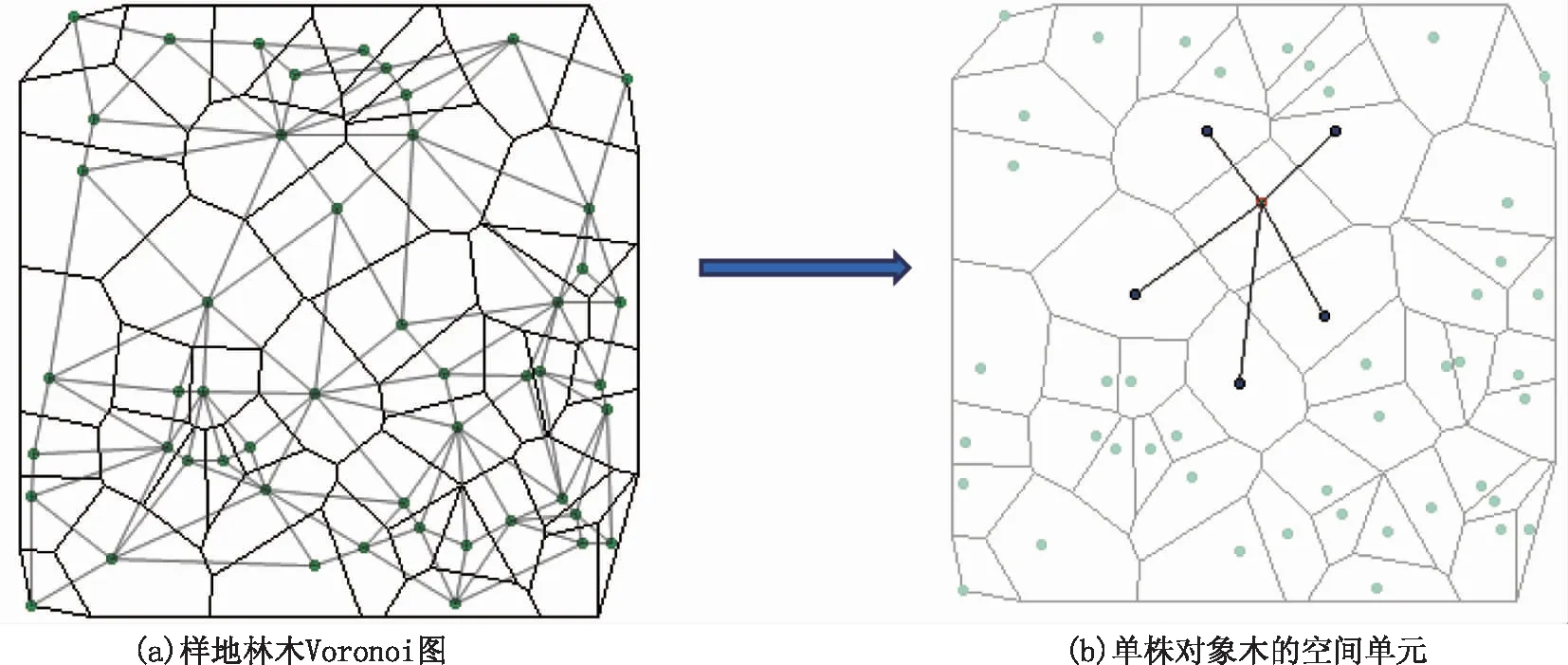
图1 样地Voronoi图及对象木空间单元

(6)
(7)
此外,Moran′s I的统计量亦用Z的得分进行显著性检验,其计算公式为:
(8)
(9)
Var(I)=E(I2)-E(I)2
(10)

2.3.2评价方案设计步骤
计算机上的专业宿舍管理系统能够有效整理和记录宿舍相关信息,大大减少人力物力,提高了信息的及时保存效率和安全性,更方便数据的查询。因而近几年来,校园里涌现出各类的信息管理系统,逐步应用到校园各类管理中[1]。为了紧跟学校的实际需求,开发出一款良好的且能投入实际使用的高校宿舍管理系统是十分有用的。它将推动学校信息化和科学化管理,特别是在交通不便、民族较多的高校显得更为重要。
文中根据Moran′s I的基本原理,在结合林木空间结构量化指标及基于Voronoi图的相邻木构建方法之上设计的林分结构空间自相关性评价步骤如下:
1)获取林木数据。包括林木编号、树种名称、胸径、树高、横纵坐标等信息。
2)构建林分空间结构单元。构建基于Voronoi图的林木空间单元,确定所有林木的相邻木,构建二维空间权重矩阵wij,若林木i和林木j相邻,则wij=1,否则wij=0。
3)根据公式(1)—(5)分别计算各对象木i的混交度、开阔比数、胸径大小比、竞争指数及综合指标的值。

5)对各样地Moran′s I的值进行评价。
依据标准正态分布,可得到Z得分所对应的概率,即P的得分[27-28],此外,根据相关文献,选取当|Z|>1.65,p<0.1时(90%置信区间),则认为该研究区域内的样本点呈明显的聚集或离散特征[28-30],一般|Z|取值越大及p的取值越小(p≥0),结果越显著。此外,为了说明各样地Moran′s I的值所代表的含义,文中参照相关文献中的方法设定的评价方案[29-30]如表3所示。

表3 林分空间结构自相关性评价标准
3 结果与分析
根据公式(1)至(5)分别计算各对象木i的混交度、开阔比数、胸径大小比、竞争指数及综合评价指标的值,并在此基础之上计算了各样地林分的平均值如表4所示。根据结果可知,调研样地中林分的平均混交度的值为0.64,表现为中混交强度;平均的开阔比数为0.48,表明该研究区域内的林分处于中拥挤状态;平均胸径大小比数为0.42,表明研究区域内的对象木和其相邻木的胸径有一定程度的差异性;平均竞争指数为1.90,表明研究区域内林木之间的竞争相对较强。此外,还根据“2.3.2”评价方案的设计步骤求解了各样地对应的Moran′s I的值,并对求解结果进行了分析。

表4 样地林分空间结构平均量化指标值
3.1 林木的混交度和开阔比数总体表现为正相关性
根据实验结果,25块调研样地中混交度的平均Moran′s I的值为0.19,平均P值为0.05,Z的平均得分为2.69,研究结果相对显著。从总体上看,样地中大部分林木的混交度与其相邻木的混交度在空间上呈正相关,在逻辑上表现为聚集分布,即若对象木i的混交度值变大,其相邻木的混交度值也会变大。但不同研究区域中林分的混交度聚集程度也有所差异,在5个研究区域地中,Moran′s I最大的区域为芦头林场,其平均值为0.26,最小的区域为龙虎山林场,其平均值为0.13。此外,龙虎山中样地L4及乌云界样地W3中,Moran′s I的值出现小于0的情况,表明这两块样地中,大部分的对象林木和其相邻木的混交度在其空间单元结构中呈负相关,表现为离散。
同理,在林木开阔比指数上,调研样地中,开阔比数的平均Moran′s I的值为0.11,平均P值为0.04,Z的平均得分为1.59,Z的值偏低,表明此数据的分布规律不明显。从总体上看,样地中大部分林木的开阔比数与其相邻木的开阔比数在空间上呈正相关,在逻辑上表现为聚集分布,即若对象木i的开阔比值变大,其相邻木的开阔比值也会变大。5个研究区域中,开阔比对应的Moran′s I的值最大的区域为龙虎山,其平均值为0.21,最小的区域为芦头林场,其平均值为0.06。此外,样地D5,LT2及LT5中,开阔比数的Moran′s I值出现小于0的情况,表明该样地中存在较多对象木的开阔比与其相邻木的开阔比在空间上呈负相关,在逻辑上表现为离散分布,样地LT3,Q5,W2及W5中开阔比Moran′s I的值等于0,表明该样地中的对象木的开阔比与其相邻木的开阔比在空间上呈随机分布,研究样地混交度及开阔比数对应的Moran′s I的值分布情况如图2和图3所示。
3.2 林木的胸径大小比和竞争指数总体表现为负相关
调研25块样地中,胸径大小比的平均Moran′s I的值为-0.20,平均P值为0.05,Z的平均得分为-2.12,表明此数据的分布规律相对比较明显。从总体上看,该研究区域中大部分林木的胸径大小比与其相邻木的胸径大小比在空间上呈负相关,在逻辑上呈离散分布,即若对象木i的胸径大小比数值越大,其相邻木的胸径大小比数的值会减少。5个研究区域中,胸径大小比Moran′s I值最大的地区为龙虎山,其平均值为-0.26,最小的区域为大围山,其平均值为-0.18。

图2 样地混交度对应的Moran′s I的值
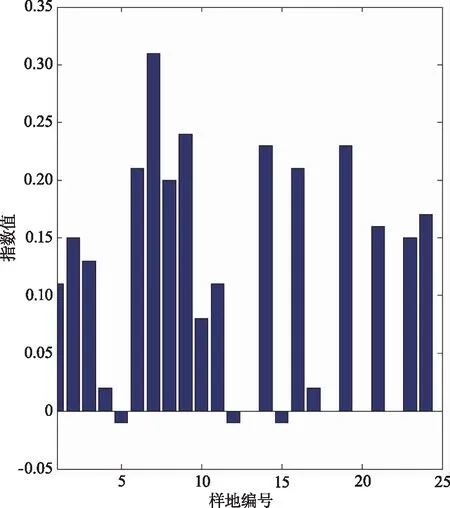
图3 样地开阔比对应的Moran′s I的值
就林木竞争指数而言,调研样地中竞争指数的平均Moran′s I的值为-0.15,平均P值为0.04,Z的平均得分为-1.95,表明此数据的分布规律相对比较明显。从总体上看,该研究区域中大部分林木的竞争指数与其相邻木的竞争指数在空间上呈负相关,在逻辑上表现为离散分布,即若对象木i的竞争指数的值越大,其相邻木的竞争指数的值就会越小。5个研究区域中,竞争指数对应的Moran′s I的值最大区域的为龙虎山,其平均值为-0.14,最小的样地为芦头林场,其平均值为-0.11。研究样地胸径大小比及竞争指数对应的Moran′s I的值分布情况如图4和图5所示。
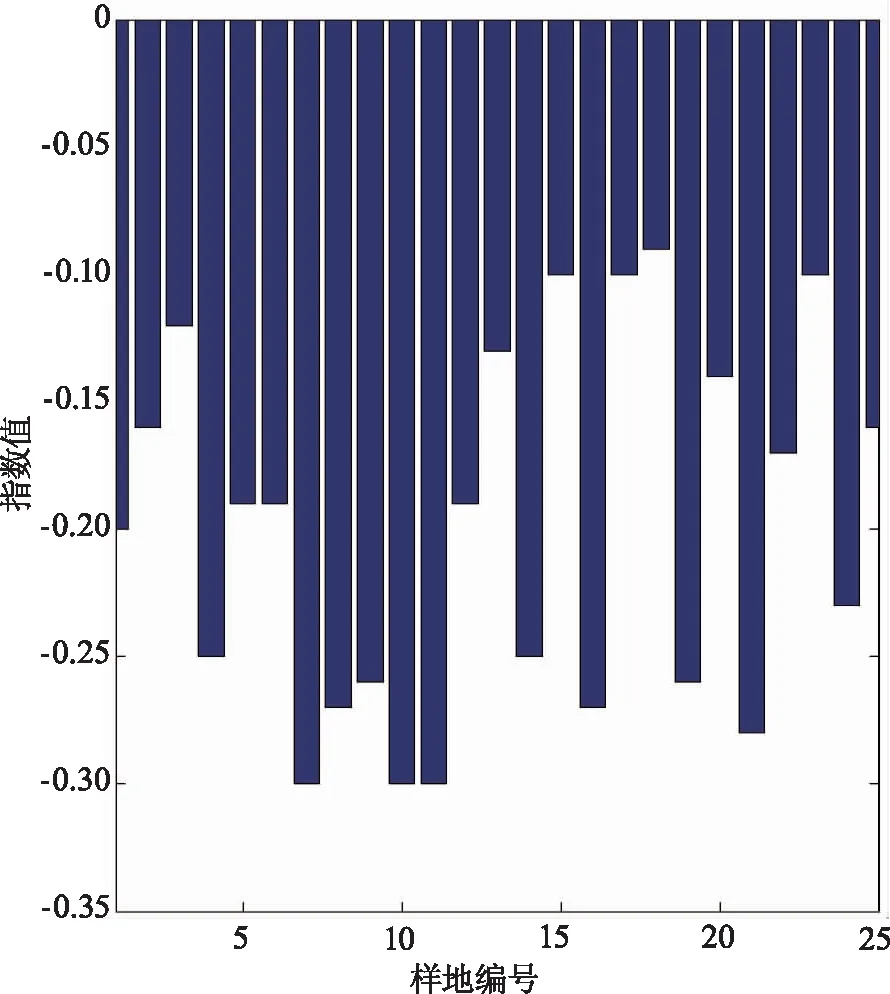
图4 样地胸径大小比对应的Moran′s I的值

图5 样地竞争指数对应的Moran′s I的值
3.3 林木在空间单元上的综合指标表现为负相关
根据实验结果,25块调研样地中林分综合指标的平均Moran′s I的值为-0.16,平均P值为0.04,Z的平均得分为-1.66,表明此数据的分布规律相对明显。从总体上看,样地中大部分林木的综合指标值与其相邻木的综合指标值在空间上呈负相关,在逻辑上表现为离散分布,即若对象木i的综合指标值越大,其相邻木的综合指标的值则会越小。在5个研究区域中,综合指标对应的Moran′s I的值最大的区域为龙虎山,其平均值为-0.18,最小的区域为乌云界,其平均值为-0.13,研究样地综合指标Moran′s I的值如表4所示。
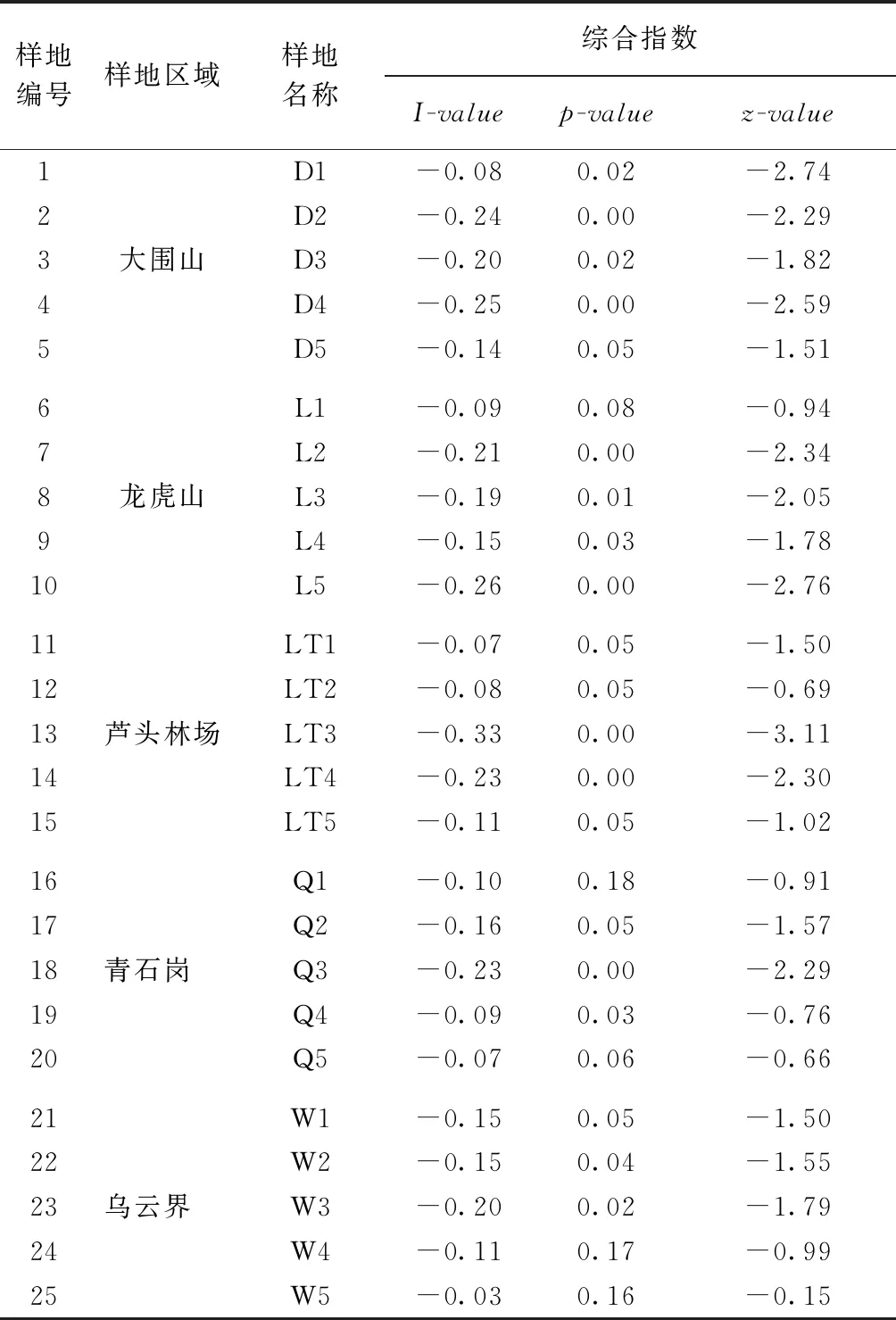
表4 研究样地综合指标Moran′s I的值
根据表4,所有样地林木综合指标对应的I-value的值均小于0,其值在(-0.15,-0.06)之间的样地为13个,占52%,在(-0.24,-0.15)之间的样地占32%,各样地林木综合指标对应的I-value值的范围分布情况如图6所示。

图6 样地综合指标对应I-value值分布情况
4 讨论与结论
4.1 讨论
如何科学量化林分空间结构中的评价指标一直是森林空间经营中所面临的难题,有学者从不同的角度提出了除文中指标之外的其它指标,比如,角尺度、林层指数、聚集指数等[31-32]。根据森林空间结构经营理论,大部分研究者在构建林分综合评价指标时一般采用各指标权重一致的方式,但事实上,对于不同的林分及不同的经营目标这些指标的重要程度可能会存在差异,然而目前对于这些量化指标重要程度的判断研究并不多。林分综合评价指标对应的Moran′s I的值可以从整体上反映该林分在空间结构上是离散还是聚集,这类影响林分在空间分布上是聚集还是离散的关键指标或许可以考虑作为林分空间经营过程中需调整其权重的参考依据。鉴于此,文中分别将25块样地中林分的混交度、开阔比数、胸径大小比及竞争指数与其综合评价指标对应的Moran′s I的值进行相关性拟合,根据实验结果,样地林分综合评价指标Moran′s I的值与其对应的混交度、开阔比数、胸径大小比及竞争指数均呈负相关,在这4个指标中,林分的混交度和竞争指数与其综合评价指标对应的Moran′s I值的拟合结果相对较明显,表明混交度和竞争指数可能是影响林分在空间单元中存在负相关的主要指标,是林分在空间结构经营过程需要考虑的对象。此外,文中依据全局Moran′s I的原理探讨了一个能整体评价林分空间结构量化指标是否存在空间自相关的方法,对于空间结构中的局部自相关问题可以通过局部Moran′s I中的相关方法进行探讨。
4.2 结论
本文在大围山、龙虎山、乌云界等自然保护区中设定了25块样地,这些研究区域内主要包括马尾松(PinusmassonianaLamb.)、香樟(Cinnamomumcamphora(Linn)Presl)、苦槠(Castanopsissclerophylla)、杉木(Cunninghamialanceolata)等树种,然后根据林分空间关系量化指标及全局Moran′s I的原理构建了一个林分空间属性自相关的评价方案,并根据调研样地中的林木数据进行了实验,主要的结论如下:
1)在空间关系上,25块实验样地中大部分林木的混交度、开阔比数与其相邻木在空间上呈正相关性,在逻辑上表现为聚集,即若对象木的混交度或者开阔比数值越大,其空间结构单元中的相邻木所对应的混交度或者开阔比数值也会变大;样地中大部分林木的胸径大小比、竞争指数与其相邻木在空间上呈负相关,在逻辑上表现为离散,即若对象木的胸径大小比或者竞争指数的值越大,其空间结构单元中的相邻木所对应的胸径大小比或者竞争指数的数值会越小。
2)根据实验样地中空间结构指标的值与其综合评价指标对应的Moran′s I的值关系可知,对象林木的混交度和竞争指数可能是导致其与周围相邻木存在负相关的主要空间指标。
