5G网络业务可靠性试验置信度分析

王军良，黄 宁，包盛花，武润升

(1.北京航空航天大学 a.可靠性与系统工程学院，北京 100191； b.云南创新研究院，昆明 650233；2.华为技术有限公司，上海 201206)

0 引 言

随着第五代移动通信技术(5th Generation Mobile Communication Technology，5G)网络等新兴网络的出现和在各个领域的应用，网络业务的可靠性问题越来越受到重视[1]。当前许多研究针对网络可靠性试验方法进行了设计[2-4]，但这些研究在设计网络试验时，缺乏规划网络可靠性试验所需要的试验时长以及求解置信区间，导致最终的试验结果可信度不高。

目前一些研究对于简单网络的置信度分析问题有相应的解决方案。如文献[5-10]假定网络对象的底层设备为具有未知平均故障间隔时间的指数型产品，通过设备之间的故障相互独立且服从泊松分布，推断整网的时延和丢包等也符合该分布特征，由此基于传统产品的置信度分析方法计算出试验结果置信区间。此外，文献[11]以威布尔分布计算了网络试验时长和置信区间问题。但对5G网络系统而言，各个构件产品的可靠不能保证上层网络业务的可靠[12]，且5G网络业务具有复杂性、故障模式多样性和部署方式动态性[13]，使得5G网络中业务的故障分布很可能不是泊松分布等固定分布形式，这就导致传统的置信度分析方法难以再应用于5G网络试验中。

在这种背景下，本文提出了一种基于业务故障分布统计的5G网络业务可靠性试验置信度分析方法，首先通过预试验收集5G网络试验数据，拟合出准确的5G网络业务故障分布，然后在此基础上对试验时长进行规划以及进行置信度分析，从而准确地求解出5G网络业务的可靠性试验时长及评估结果置信区间。

1 网络业务故障分布规律的确定

对于5G网络业务故障而言，由于网络中存在软件的调用和业务的资源分配等，其故障分布规律往往与单纯的硬件故障不同，难以直接确定故障符合何种分布规律。因此，这里首先进行一定量的预试验，收集网络可靠性数据；然后从预试验的故障数据中找出理论网络故障分布的表达式；最后进行故障分布规律的验证。

1.1 预试验数据收集

先进行多组预实验，收集首次5G网络故障时的预试验数据。该步骤的目的主要是确定预试验的单组试验持续时间。

为了方便故障数据的收集，在每一组预试验中，需要统计网络首次故障发生时间作为网络的故障间隔时间值，进行多组预试验后得到单组预试验需要进行的时间。网络首次故障发生时间的统计方法如图1所示。图中，Dmax为网络试验中故障判据的参数阈值，单位依照参数类型确定；Δt为网络参数采样间隔，单位为s。

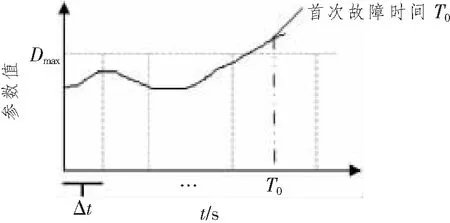
图1 预实验数据统计方法

在多个网络首次故障时间中，选取一个最大的网络首次故障时间作为单次预试验的时间T0，然后再进行m组预试验，每一组预试验的时间为T0。m的取值会影响故障规律的精确度，因此其与后续置信度分析相关。进行完m组预试验后，对整个预试验时间区间T0，统计在每一个Δt间隔内的故障发生频率，通过常用的经验估计法(即使用频率来代替故障发生概率)，得到预试验数据点集G：

式中：i为点的序号；pi为经验估计法获得的频率；ci为在时间段(i-1)Δt～iΔt内，有网络故障发生的预试验组数。显然，Δt的取值会影响数据集G的数据量，从而影响拟合的精度。由中心极限定理，假设已经拟合得到的故障规律为F,对应真实故障规律为F*，当点集中的数据与真实分布的误差独立同分布，Δt的取值对拟合规律造成的误差满足：

式中：zC为置信度为C下的上分位数；σ为点集中pi的均方差。由式(2)可知，故障规律的拟合精度与Δt的平方根呈反相关。

此外，使用频率代替概率，也会不可避免地引入估计误差，导致数据点集不精准的问题。假设pi对应的真实概率值为qi，且其中状态数k为2(正常和故障两种)，则估计误差ε可表示为

1.2 预试验数据切分

在进行完一定量预试验后，可以收集到少量的5G网络可靠性试验数据集G，这些数据需要被用来分析故障规律，同时用于对确定的故障规律进行验证。为了保证验证的客观性，需要将预试验数据集G切分出独立的一组，即

式中：[FitSet]为拟合出的故障规律；[ValSet]为测试得到的故障规律对实际规律的拟合程度。

通常情况下需要进行多次故障规律的拟合。重复的数据利用可能会出现重复拟合和过拟合的现象，为避免出现这两种情况，需要将[FitSet]分成多个小组，分别得到各个小组的故障规律，然后使用[ValSet]进行验证，最后取出验证结果最好的一个故障规律：

注意到，由于预试验得到的试验数据较少，如果如上述分组进行拟合，每组的数据量可能不足以得到准确的模型，这里可以使用交叉验证的思想对数据进行充分利用，即某组拟合数据进行拟合后，可以再次被用作验证数据。

1.3 网络故障分布规律拟合

拟合过程有两种选择。首选的拟合方式是根据预试验中m组预试验得到的故障数量统计，直接预估5G网络故障分布所有可能的模型形式，如钟形的曲线可以假设为符合正态分布等；然后根据这些预估的模型形式，仿照传统的统计方案进行计算。该方法适合与传统故障分布类似的网络，得到的分布准确性较高，适用于可以直接套用已有分布规律的情况。

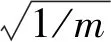
2 网络试验时长和置信区间的确定

根据以上得到的网络故障分布规律，就可以按照给定的置信度信息确定出需要进行的5G网络可靠性试验时长。同时，根据试验时长和置信度信息，进一步可以得到平均无故障间隔时间等可靠性参数在该置信度下区间的上下限。

2.1 试验时长的计算

在进行试验时长计算之前，首先规定以下符号含义：θ0为生产方可接受质量水平；θ1为使用方要求的平均无故障间隔时间(Mean Time Between Failure，MTBF)；α为生产方风险；β为使用方风险。以上几个数值在进行预实验前需要根据客户和网络提供方的要求给定数值。θ为待确定MTBF的真实数值；最终的待求结果中R0为统计方案接收时的网络故障数；T为统计方案接收时进行的试验时长。在已经求得故障发生概率函数F(ω,t)的前提下，可以通过联立方程求取试验时长。

取R(ω,t)=1-F(ω,t)。根据数理统计原理，接受概率P(θ)为

依照风险系数的定义，有以下关系式成立：

在式(6)和(7)中，未知数为接收网络故障数R0和试验时长T，方程数与未知数相等，因此该式理论可解。通过求解方程，最终得到R0和T。

当P(θ)表达式复杂，难以直接求解方程时，可以采用迭代的方法计算R0和T。为方便计算，令拒收故障数为R1=R0+1。具体而言有以下步骤：

(1) 初始值R0= 0，R1=1。

(2) 将R0和规定的θ1与β值代入式(7)的第2个等式，得到可能的最小试验时长T。

(3) 将T值、R1值与规定的θ0代入式(7)的第1个等式，计算出α′的值。

(4) 分支步骤。若计算出的α′大于规定值α，让R0与R1的值都加1，并转入步骤(2)；若不大于，则转入步骤(5)。

(5) 停止迭代，输出要求的T、R0和R1。

通过上述迭代也可以得到R0和T。得到了这两个数值之后，就可以合理地规划网络可靠性试验并进行试验，获取更多的试验数据。

2.2 置信区间分析

一般而言，置信度C的建议值在(1-2β)×100%左右。5G网络的试验者也可根据客户方面的要求适当提高或降低给定置信度，数值越高，得到的MTBF的置信区间会越大，而过大或过小的置信区间都不具备参考价值。

为了避免混淆，将上一节中得到的接受概率P(θ)设为Q(θ)。在给定置信度C后，对于待求置信下限θL和置信上限θU，满足：

一般而言，当Q(θ)的表达式不符合泊松分布和正态分布等特殊情况时，θL和θU并不容易求得。为此，当故障规律函数F(ω,t)波动幅度不大时，根据概率统计原理，可以进行如下的近似计算：

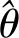
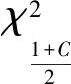
(1) 收集可靠性试验得到的故障时间间隔参数的点集H。在进行完试验后，可以得到较大规模的待估计MTBF参数的样本。

(2) 不断从参数点集中随机抽取样本值，作为新的点集H*中的元素。

式中：n为收集到的故障样本量；tC/2为C/2置信度下的t分布值。一般而言，当F(ω,t)波动不大时，建议采用直接计算的方式得到置信区间，得到的结果准确且耗费时间较少；只有当F(ω,t)波动较大时，才可采用Bootstrap方法，通过模拟抽样，得到置信区间，其准确性依赖于点集H*的元素个数，元素越多，准确性越好，计算耗费时间越多。

3 案例分析

以部署于洋山港的一个基于5G网络轮胎吊(Rubber Tired Gantry，RTG)远程控制业务的可靠性试验为例，说明上述方法的具体应用方式。在进行可靠性试验置信度分析之前，假定已对该网络业务完成了网络故障判据的确定和试验剖面的设计。基于该前提，就可以通过上述方法对网络试验进行试验时长计算和置信度分析。

3.1 RTG远程控制业务故障分布规律

在本节中，需要通过一定量的预试验，确定出5G网络上RTG远程控制业务的故障分布规律，为之后试验时长和置信区间的分析做准备。

图2所示为确定网络业务故障分布规律图。首先进行k组实验，对于确定累计故障分布的预实验，实验的组数k与每组时长N×Δt的选取要在满足1.1节精度的要求下进行。这里k的取值为1 500次，已经满足精度要求。

图2 确定网络业务故障分布规律

对于每组实验，收集业务参数(以RTG大车定位偏差D大车为例)的具体数值作为业务的故障判据。定义采样时间间隔为Δt，且满足精度要求的最小Δt为1 s。若在采样时刻，采集的定位误差数据大于定位误差阈值，则认为故障发生。对于每组实验，收集其初次故障时间，然后统计这k组实验中初次故障时间在每个时间点上出现的频率，确定业务故障的故障概率分布。

通过累计故障率分布的统计图，进一步可以通过数据拟合的方式，计算拟合出该曲线的函数表达。根据Han的调研文献中有关吊车故障的数据来进行拟合[15]，拟合的图形如图3所示，图中，横轴是试验时间，纵轴是业务正常运行的频率值p_value，粉色点为模拟的故障数据点集，拟合出的曲线(蓝色曲线)趋近于水平线。

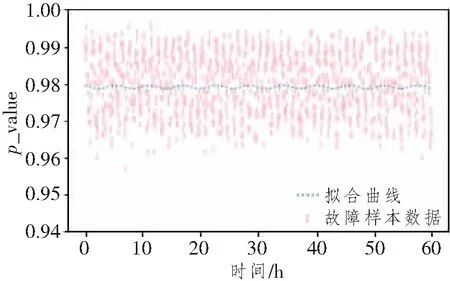
图3 拟合故障数据

3.2 RTG远程控制业务网络试验时长和置信区间计算

通过3.1节的预试验故障分布规律F(ω,t)，注意到该函数几乎趋近于水平线。因此，如果其网络故障判据只取决于一个参数(如“大车定位偏差”)，则故障分布服从二项分布。而在本案例中，故障判据取决于多个参数，则其故障分布服从多维二项分布。

针对RTG远程操控业务的可靠性，需要预先确定生产方风险α、使用方风险β、检验下限R1和检验上限R2。在本案例中，给定的α与β均为10%，R2为0.999 0。

根据2.1节中对试验时长求取的方法描述，本案例中正式试验所需的样本量可通过以下方程组求得：

式中：c为接收拒收故障判据；N为正式试验所需样本量；r为试验中的故障个数。N必须为整数，此联立方程无普遍公式可解。通过对式(11)的迭代计算，可得到应得试验样本量为206 000。假设网络试验数据采样间隔为1 s，则得到c为5，总的试验时长为206 000×1 s即57.2 h。

通过2.2节中的分析，可以将求得的试验时长T和接收拒收判据c代入式(12)，直接得到RTG远程控制业务的平均无故障间隔时间置信区间为

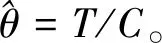
为了验证上述结果的正确性，参考5G实际案例[16]，本文构建了实际5G网络RTG业务并进行了试验(试验编号为C3-C10)，得到的可靠性试验结果如图4所示，由图可见，试验结果实际值基本在该区间内(即上下两条虚线内)，符合置信度分析的预期值。

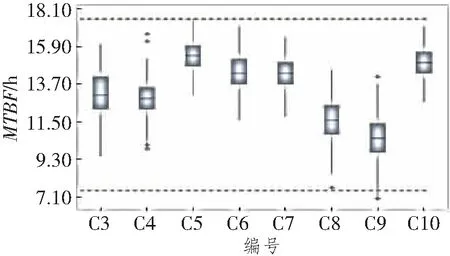
图4 可靠性试验结果箱型图与置信区间验证

4 结束语

本文的网络可靠性试验置信度分析对5G网络故障规律进行了预先的确定，在满足精度要求的前提下，通过一定量的预试验，拟合试验结果数据，得到故障分布函数F(ω,t)。传统的置信度分析中往往直接采用泊松分布计算试验时长，并进一步分析置信区间，而对于5G网络这类复杂的网络而言，其动态性和耦合性等特征致使故障分布往往不符合泊松分布等传统分布，因此传统产品的可靠性试验置信度分析应用于5G网络时，必然会导致不精确的结果，而本文所提方法通过预试验和故障规律的拟合，得到了相对精确的故障规律，由此通过置信度分析得到的试验时长和结果置信区间等更为精确，更具可信性。