基于剪切松弛试验的沥青低温劲度模量反演方法
2022-03-29杜镇宇毛菊良肖飞鹏
王 勤, 杜镇宇, 毛菊良, 肖飞鹏, 袁 捷
(1.上海同济检测技术有限公司,上海 200092;2.同济大学道路与交通工程教育部重点实验室,上海 201804;3.同济大学民航飞行区设施耐久与运行安全重点实验室,上海 201804;4.中国民用航空飞行学院 机场学院,四川 广汉 618307)
沥青路面的低温开裂一直是道路工程中常见的病害之一.用于沥青低温性能评价的方法很多,例如延度试验[1]、测力延度试验[2-3]、玻璃化转化温度试验[4]、弗拉斯脆点试验[5]等.但是,不同方法均存在其缺陷和局限性.弯曲梁流变仪(BBR)试验是美国公路战略研究计划(SHRP)提出的沥青低温性能评价手段[6],该试验广泛应用于高校及科研机构.但是,该试验中沥青小梁样本制作过程较繁杂,且沥青用量较多,制样方法对测试结果的影响显著[7].由于动态剪切流变仪(DSR)制样方便且测试方法简单,越来越多的研究人员开始采用DSR 对沥青的低温性能进行评价.Sui 等[8-9]基于DSR,利用4 mm 转子,通过频率扫描获得松弛模量主曲线,进而评价沥青的低温性能;王超[10]则采用DSR 评价老化对沥青低温性能的影响.但是,在实际研究过程中,更多使用的是8 mm 转子和25 mm 转子,且做主曲线的过程较繁琐.
综上,越来越多研究人员开始采用DSR 对沥青的低温性能进行评价,但不同的试验方法和评价指标均存在一些局限性.因此,本文基于DSR 试验设备,采用8 mm 转子,在低温下直接进行剪切松弛试验,获取低温剪切松弛模量,反演出劲度模量Sshear和模量变化率mshear,并将其与弯曲梁流变仪实测的劲度模量S和模量变化率m进行对比分析,以证明该方法的可靠性,为改性沥青低温性能评价提供参考.
1 试验
1.1 原材料
沥青来源分别为山东京博沥青(JB-70#)和2 种针入度的90#辽宁盘锦沥青(PJ-90#A 和PJ-90#B).所采用的聚乙烯改性剂为中石化生产的低密度聚乙烯(LDPE),掺量(质量分数)分别为2%、4%、7%,对应沥青试件编号形式为“沥青标号-LDPE 掺量”.SBS 改性沥青为道路工程中常用的厂拌成品I-D 级改性沥青(SBS-I-D).
1.2 试验方法
1.2.1 弯曲梁流变仪(BBR)试验
弯曲梁流变仪采用Canon 公司生产的弯曲梁流变仪.试验温度设置为-6 ℃,小梁试件尺寸为长127.00 mm、高6.35 mm、宽12.70 mm.试验过程中的跨中荷载为(980±50)mN.试件浇筑前,所有沥青样品均先进行短期老化(RTFOT),后进行长期老化(PAV).
1.2.2 剪切松弛试验
采用英国Malvern 公司生产的动态剪切流变仪(DSR),所有沥青试样均进行短期老化(RTFOT)和长期老化(PAV),再进行剪切松弛试验.
(1)试验温度的确定 考虑到仪器低温加载范围的限制,同时也为了和BBR 所得低温劲度模量进行比较.基于动态剪切流变仪进行剪切松弛试验时,将温度设为-6 ℃.
(2)剪切应变的确定 根据BBR 的试验结果可知,随着LDPE 掺量的增加,改性沥青模量不断增大,且标号越高的改性沥青模量越小.考虑到低温条件下进行剪切松弛试验时,过大的应变会造成材料的损伤;另外,由于仪器本身的限制,过小的应变会造成较大误差.因此,分别采用0.1%、1.0%及10.0%的加载应变,对模量最大的JB-70#-7%改性沥青在-6 ℃下进行剪切松弛试验,进而确定加载应变,试验结果见图1.由图1 可见:在0.1%和1.0%的加载应变下,各应力-时间曲线趋势一致,均为应力随加载时间延长而增大,到某一峰值后应力开始减小;而在10.0%的加载应变下,曲线出现1 个水平段,这可能是在低温下,过大的加载应变造成了材料的破坏,故排除10.0%的加载应变.

图1 JB-70#-7%沥青在不同加载应变下的松弛应力Fig.1 Relaxation stress of JB-70#-7% asphalt under different loading strains
为了进一步比较0.1%和1.0%加载应变,在2 种加载条件下进行多次重复试验,结果见图2.由图2 可知:在较小的加载应变(0.1%)下,剪切应变波动范围较大,最大超过10.0%;而在较大的加载应变(1.0%)下,应变-时间曲线更稳定.

图2 JB-70#-7%沥青在不同加载应变下的剪切应变Fig.2 Shear strain of JB-70#-7% asphalt under different loading strains
综上所述,在进行剪切松弛试验时,选择1.0%的加载应变.
(3)剪切时间的确定 考虑到仪器所能承受的降温范围,所有沥青试样均先在-6 ℃下保温10 min,再进行松弛,松弛时间为10 min.
1.3 理论基础
1.3.1 模量反演思路
劲度模量反演的主要思路如下:通过DSR 进行低温剪切松弛试验,获取沥青的剪切松弛模量,利用广义Maxwell模型对其进行拟合,再根据松弛模量与蠕变柔量之间的关系,分别利用Matlab 软件和人为求解析解的方法对蠕变柔量进行求解,进而反演得到劲度模量;再利用BBR 实测劲度模量和模量变化率对反演结果进行验证分析.
1.3.2 通过松弛模量求解劲度模量
1.3.2.1 解析解法
采用五参数广义Maxwell 模型对剪切松弛试验获得的松弛模量E进行拟合,其表达式如下:

式中:E0、E1、E2均为弹簧拟合参数;η1、η2均为黏壶拟合参数;t为时间.
由Boltzman 叠加定理[11]可知:

式中:(s)为蠕变柔量的拉普拉斯变换结果;(s)为松弛模量的拉普拉斯变换结果;s为拉普拉斯域变量.
将式(1)进行拉普拉斯变换,得:

则:

上式必可写成以下形式:
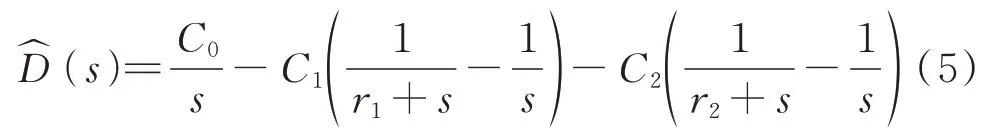
式中:C0、C1、C2、r1、r2均为待定系数,可通过比较式(4)、(5)的系数求解.
令:

则:

进而将式(5)做拉普拉斯逆变换,可得劲度模量Sshear1:

式中:L-1为拉普拉斯逆变换算符.
式(8)所得Sshear1为通过解析解法求得的沥青劲度模量.
1.3.2.2 Matlab 法
通过Matlab对式(4)直接进行拉普拉斯逆变换,可得:
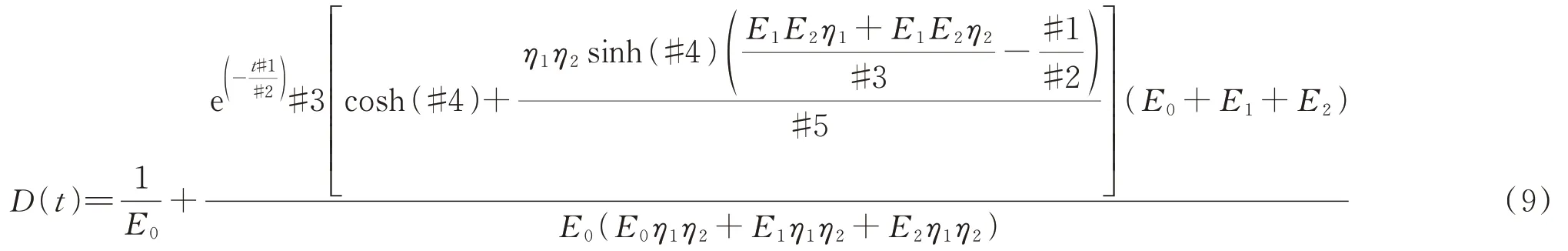
其中:
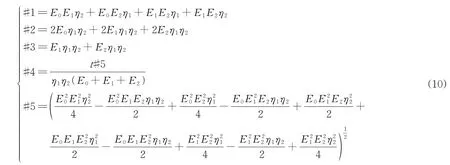
求得蠕变柔量D(t)后,进而求其倒数得到沥青的劲度模量Sshear2.
1.3.3mshear的计算
借鉴弯曲梁流变仪对m值的定义[12],计算反演得到的劲度模量Sshear1在60 s时的变化率,记作mshear.
2 反演及实证分析
-6 ℃下不同沥青的剪切松弛模量见图3.由图3可知,松弛能力最强的是PJ-90#A 基质沥青,最差的是JB-70#-7%LDPE 改性沥青.利用五参数广义Maxwell 模型(式(1))对图3 中不同改性沥青的松弛模量进行拟合,计算结果见表1.
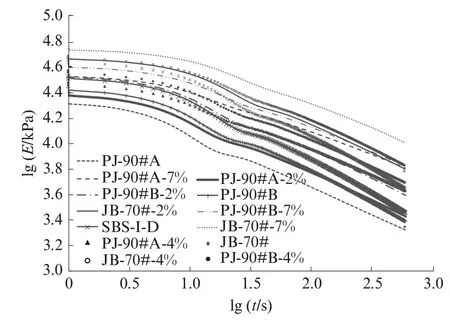
图3 -6 ℃下不同沥青的剪切松弛模量Fig.3 Shear relaxation modulus of different asphalt binders at-6 ℃
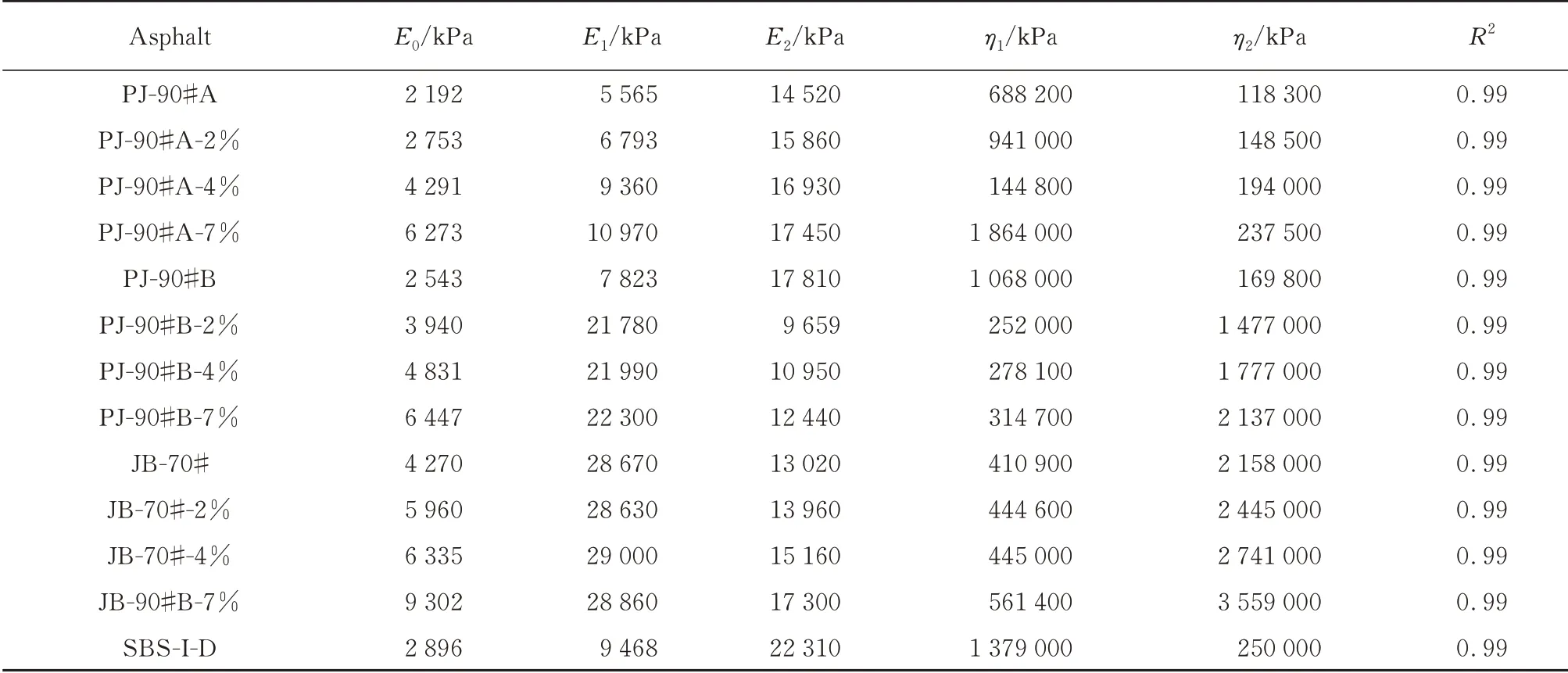
表1 各沥青实测松弛模量拟合结果Table 1 Fitting results of measured shear relaxation modulus of asphalts
由拟合所得方程,通过1.3.2 中2 种劲度模量反演方法计算不同沥青的劲度模量,由其直观表达式可知,二者并不一致.为比较2 种方法所得结果的一致性,以PJ-90#A 沥青为例,将2 种方法所得结果作差,如图4 所示.由图4 可知,2 种方法所得劲度模量之差绝对值在近10-9MPa 量级范围内,故可认为2 种方法所得结果大小相当.因此,在劲度模量反演的过程中,可利用Matlab 将实测的剪切松弛模量直接做拉普拉斯逆变换后再对劲度模量进行求解,这样可避免人为求解析解的复杂计算过程.后文所用反演劲度模量Sshear均为Matlab 求解结果.

图4 2 种方法对PJ-90#A 基质沥青劲度模量反演结果之差Fig.4 Difference of stiffness modulus of PJ-90#A base asphalt calculated by two methods
BBR 实测劲度模量S与反演劲度模量Sshear对比见图5.由图5 可知:反演劲度模量与实测劲度模量的曲线形式和趋势基本一致,但二者的绝对值并不相同;S/Sshear比较稳定,约为一直线,其均值大概在4.5 左右,如图5(c)所示.这可能是由于2 种加载模式的不同而造成的:DSR 剪切松弛试验的加载模式为旋转剪切,而BBR 的加载模式为弯拉.
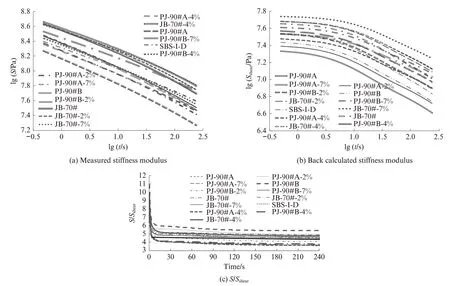
图5 BBR 实测劲度模量S 与反演劲度模量Sshear对比Fig.5 Comparison of BBR measured and back calculated stiffness modulus
取不同沥青在60 s 时的实测劲度模量与反演劲度模量进行对比,结果如图6 所示.由图6 可知,通过剪切松弛试验反演所得劲度模量与BBR 实测劲度模量之间具有较好的线性关系,故可以通过剪切松弛试验来预估沥青低温下的劲度模量.

图6 不同沥青在60 s 时的实测劲度模量与反演劲度模量Fig.6 Measured and back calculated stiffness modulus of different asphalts at 60 s
将各沥青60 s时的反演劲度模量Sshear和实测劲度模量S进行排序,结果见表2.由表2 可知,2 种劲度模量的排序基本一致,Kendall秩相关系数达0.923 1,故可以通过反演劲度模量来大致比较不同沥青的劲度模量.
不同沥青在60 s时的实测劲度模量变化率m与反演变化率mshear见图7.由图7可知,二者具有较强的线性关系,相关系数R2达到了0.99,比例系数为1.1.说明可以通过mshear的值对m进行估计,将二者数值从小到大进行排序,结果也列于表2.由表2可见,其Kendall秩相关系数达0.871 8,说明二者的一致性较高.

表2 各沥青60 s 时的劲度模量及其变化率排序Table 2 Sequence of stiffness modulus and its change rate of asphalts

图7 不同沥青在60 s 时的劲度模量变化率m 与反演变化率mshearFig.7 Measured and back calculated stiffness modulus change rate of different asphalts at 60 s
3 结论
(1)解析解和Matlab 解这2 种劲度模量反演方法表达式不同,但计算结果误差范围在近10-9MPa量级范围内,可认为二者所得结果一致.故可利用Matlab 直接做拉普拉斯逆变换来反演得到沥青的劲度模量,省去人为求解析解的复杂计算过程.
(2)反演劲度模量与实测劲度模量曲线形式和趋势一致,且二者之间存在稳定的比值关系,比值的均值约为4.5,这可能是由于动态剪切流变仪剪切松弛试验为旋转剪切加载,而弯曲梁流变仪试验为弯拉加载所致.
(3)不同沥青60 s 时的反演劲度模量与BBR 实测劲度模量具有较强的线性关系,其比例系数在4.5左右,劲度模量变化率反演结果与实测结果的比例系数为1.1.从Kendall 秩相关系数来看,反演结果与实测结果具有良好的一致性.
(4)由于有限的试验量,反演劲度模量与实测劲度模量及其变化率的比例系数有待于更多种类改性沥青的进一步修正,且其他温度条件有待后续进一步研究.
