掺粉煤灰再生混凝土吸湿过程与预测模型研究

2022-03-29蒋建华付用全林明益

建筑材料学报 2022年3期

蒋建华，吴琦，付用全，林明益，眭源

（河海大学土木与交通学院，江苏南京 210024）

再生混凝土技术将废旧混凝土进行二次利用，有利于维护生态环境的平衡和社会的可持续发展.但现有研究表明再生混凝土的耐久性往往低于天然混凝土，如何改善再生混凝土的耐久性能已成为学术界关注的热点［1-3］.

混凝土内部湿度环境是影响混凝土耐久性能的主要因素之一［4-6］.混凝土内部的含湿状态很大程度上取决于对外部气候环境的响应.Zhang 等［7］和Min等［8］研究了人工恒定气候环境下荷载损伤普通混凝土的内部湿度响应规律.Andrade 等［9］和王卫仑等［10］开展了自然气候环境下普通混凝土的内部湿度响应规律研究.Liu 等［11-12］研究了不同温度及荷载条件下再生混凝土的内部湿度响应规律和机理.由此可见，目前关于混凝土内部湿度响应的研究主要集中于普通混凝土，再生混凝土湿度响应的研究还有待进一步完善.

本文在前期研究成果［13］的基础上，基于恒定气候环境条件的吸水试验和湿度响应试验，进一步研究了考虑再生粗骨料取代率、粉煤灰掺量和再生粗骨料初始含水率3 种影响因素对混凝土内部湿度响应的影响，并进行了模型预测，以期为后续再生混凝土结构的耐久性定量分析提供理论基础.

1 试验

1.1 原材料与试件设计

水泥为P·O 42.5 普通硅酸盐水泥；粉煤灰（FA）为Ⅱ级F 类粉煤灰；细骨料为河砂（中砂），细度模数为2.7；天然粗骨料（NCA）为粒径5～15 mm 的碎石；再生粗骨料（RCA）产自南京富源资源利用有限公司，粒径范围为5～15 mm；拌和水为普通自来水；减水剂（WR）为聚羧酸系液态减水剂.立方体试件尺寸为100 mm×100 mm×100 mm，其水胶比为0.40（质量比，文中涉及的水胶比、含水率等均为质量比或质量分数）.本文设计3 组试验工况：（1）固定粉煤灰掺量ρF为20%、再生粗骨料初始含水率ωR为4.50%，考虑不同再生粗骨料取代率ρR（0%、25%、50%、75%、100%）的影响；（2）固定ρR为100%、ωR为4.50%，考虑不同ρF（0%、10%、20%、30%）的影响；（3）固定ρR为100%、ρF为20%，考虑不同ωR（0%、3.56%、5.76%、7.83%）的影响.混凝土试件配合比如表1所示.

表1 混凝土试件配合比Table 1 Mix proportions of concrete specimens kg/m3

1.2 试件制作与养护

本文采用PVC 管预留孔洞埋置湿度传感器来测量混凝土的内部相对湿度.浇筑混凝土时，为避免水泥浆渗入管内，预先将尼龙棒插入PVC 管中.试件制作前，为使再生粗骨料具有一定梯度的初始含水率，先将再生粗骨料于105 ℃下烘干24 h，再满水浸泡12 h；然后将粗骨料分为4 组，再次进行烘干处理，每组烘干时间分别为0、1、3、5 h；最后静置至室温后称重，计算得到4 组再生粗骨料的含水率，分别为0%、3.56%、5.76%、7.83%.考虑到4 组再生粗骨料初始含水率的不同，为保持试件水胶比一定，混凝土搅拌时减少相应拌和水的用量.

吸水试件采用普通塑料模具进行浇筑；湿度响应试件采用侧面开孔的木模具进行浇筑.试件浇筑24 h 后拆模，然后在标准养护条件（（20±2）℃，相对湿度95%以上）下养护28 d，最后在室内静置60 d，待水泥充分水化.

1.3 试验方法

1.3.1 吸水试验

混凝土的吸水特性与材料自身的孔隙结构及分布密切相关.为便于分析相关因素对混凝土内部湿气传输的影响机理，本文先开展混凝土的吸水试验.试验前，为模拟混凝土试件处于完全干燥状态，先将试件置于105 ℃的电热恒温干燥箱中进行干燥处理，每隔24 h 记录1 次试件的质量变化，当连续2 次的质量差小于1 g 时，视为试件完全干燥，将试件此时的质量记为m0.试件干燥完成后，在相同工况下选取2个试件进行吸水试验，取吸水量的平均值作为代表值.试验装置采用设有固定圆柱体支架的水箱，为保证试件暴露面与水能够充分接触，控制水面高于混凝土暴露面3 mm 左右，水温为（20±2）℃，混凝土吸水试验示意图如图1 所示.为反映试件早期吸水特性，在试验初期的7 h 内每隔1 h 称重1 次；随后每隔24 h 称重1 次，连续测量10 次，共17 次；试件质量记为mi，质量差即吸水量Δmi=mi-m0（1 h＜i≤240 h）.

图1 混凝土吸水性试验示意图Fig.1 Schematic diagram of water absorption test of concrete（size：mm）

1.3.2 湿度响应试验

湿度响应试验前，为控制试件的初始相对湿度，同样先将试件置于105 ℃的干燥箱中烘干处理；然后置于恒定温湿度环境中，采用温湿度传感器监测混凝土内部温湿度条件；最终使混凝土内部的初始相对湿度在试验温度下达到（50±3）%.试件干燥完成后，拔出PVC 管中的尼龙棒，插入湿度探头（测量范围0%～100%，测量精度±（2～3）%，分辨率0.1%），先用带槽口的橡皮塞密封PVC 管口，再用生料带和铝箔胶带进行密封；为模拟一维吸水和湿度响应过程，将试件除暴露面外的其余5 个面用铝箔胶带密封；最后将湿度探头与记录仪连接，如图2 所示.试件处理完成后，将其置于恒温恒湿箱中进行湿度响应试验.模拟混凝土试件吸湿过程的湿度响应条件为：试件初始相对湿度H0=50%，环境相对湿度He=90%，环境温度T=25 ℃.湿度记录仪设置为每隔6 h记录1 次，记录时长30 d.

图2 混凝土湿度响应试验示意图Fig.2 Schematic diagram of humidity response test of concrete（size：mm）

2 吸水试验结果与分析

2.1 吸水量的时变规律

在水胶比为0.40 的条件下，分别研究再生粗骨料取代率（ρR）、粉煤灰掺量（ρF）及再生粗骨料初始含水率（ωR）对混凝土吸水量的影响.3 种影响因素下混凝土的吸水量时变曲线如图3 所示.由图3 可知：3 种影响因素下混凝土早期吸水量均增长较快，随着吸水时间（tw）的延长，混凝土的吸水量增速逐渐减慢，最终趋向稳定；当吸水时间（tw）一定时，ρR为25%的混凝土吸水量最小，ρR为0%、50%、75%和100%的混凝土吸水量依次增大；ρF为10%的混凝土吸水量最小，ρF为0%、20%和30%的混凝土吸水量依次增大；随着ωR的增大，混凝土的吸水量逐渐增大.

图3 混凝土吸水量时变曲线Fig.3 Time-dependent curves of water absorption of concrete

2.2 毛细吸水系数

图4为混凝土单位面积（A）吸水量（Δmi/A）与吸水时间（tw）平方根的关系曲线.根据该关系曲线，进一步研究3 种影响因素对混凝土毛细吸水系数（S，kg/（m2·h0.5））的影响.混凝土吸水量与其毛细吸水系数的关系式如（1）所示［14］.

由式（1）可知，混凝土单位面积吸水量与吸水时间的平方根之比即为混凝土毛细吸水系数.在实际混凝土吸水过程中，毛细吸水系数随吸水时间而变化.为定量分析混凝土的吸水特性，将毛细吸水系数视为常数，根据式（1），由两者关系曲线（图4）前期线性段的斜率即可得到混凝土的毛细吸水系数，结果如图5 所示.

图4 混凝土单位面积吸水量与吸水时间平方根的关系曲线Fig.4 Curves of water absorption per unit area vs square root of time of concrete

由图5（a）可知：（1）随着ρR的增大，混凝土的毛细吸水系数先减小后增大.（2）当ρR小于25%时，混凝土的毛细吸水系数随着ρR的增大而减小；当ρR大于25%后，混凝土的毛细吸水系数随着ρR的增大而增大.（3）ρR为0%、50%、75%和100%的混凝土毛细吸水系数较ρR为25% 时分别增大了28.4%、44.8%、46.9%和52.9%.这说明ρR为25%的混凝土微观结构最为致密，而ρR为0%、50%、75%和100%的混凝土内部孔隙依次增大.

图5 混凝土的毛细吸水系数Fig.5 Capillary water absorption coefficient of concrete

由图5（b）可知：（1）随着ρF的增大，混凝土的毛细吸水系数先减小后增大.（2）当ρF小于10%时，混凝土的毛细吸水系数随着ρF的增大而略有降低；当ρF大于10%时，混凝土的毛细吸水系数随着ρF的增大而显著增大.（3）ρF为0%、20%和30%的混凝土毛细吸水系数较ρF为10%时分别增大了8.0%、15.2%和23.6%.这说明ρF为10%的混凝土微观结构最为致密，ρF为0%、20%和30%的混凝土孔隙率依次增大.

由图5（c）可知：（1）随着ωR的增大，混凝土的毛细吸水系数逐渐增大.（2）ωR为3.56%、5.76% 和7.83%的混凝土毛细吸水系数较ωR为0%时分别增大了13.7%、24.9%和27.1%.这说明混凝土的孔隙率随着ωR的增大而增大.

3 湿度响应试验结果与分析

3.1 相对湿度的时变规律

在水胶比为0.40 的条件下，分别研究再生粗骨料取代率（ρR）、粉煤灰掺量（ρF）及再生粗骨料初始含水率（ωR）对混凝土湿度响应的影响.同种工况下选取2 个试件湿度响应试验值的平均值作为代表值.混凝土内部相对湿度（H）响应曲线如图6 所示.由图6可知：（1）3 种影响因素下混凝土内部相对湿度均严重滞后于环境相对湿度（He=90%），且混凝土内部相对湿度增长速率均随试验的进行逐渐下降.（2）当湿度响应时间（t）一定时，ρR为25%的混凝土内部相对湿度值最小，ρR为0%、50%、75%和100%的混凝土内部相对湿度依次增大；ρF为10%的混凝土内部相对湿度最低，ρF为0%、20%和30%的混凝土内部相对湿度依次增大；混凝土内部相对湿度随ωR的增大而增大.

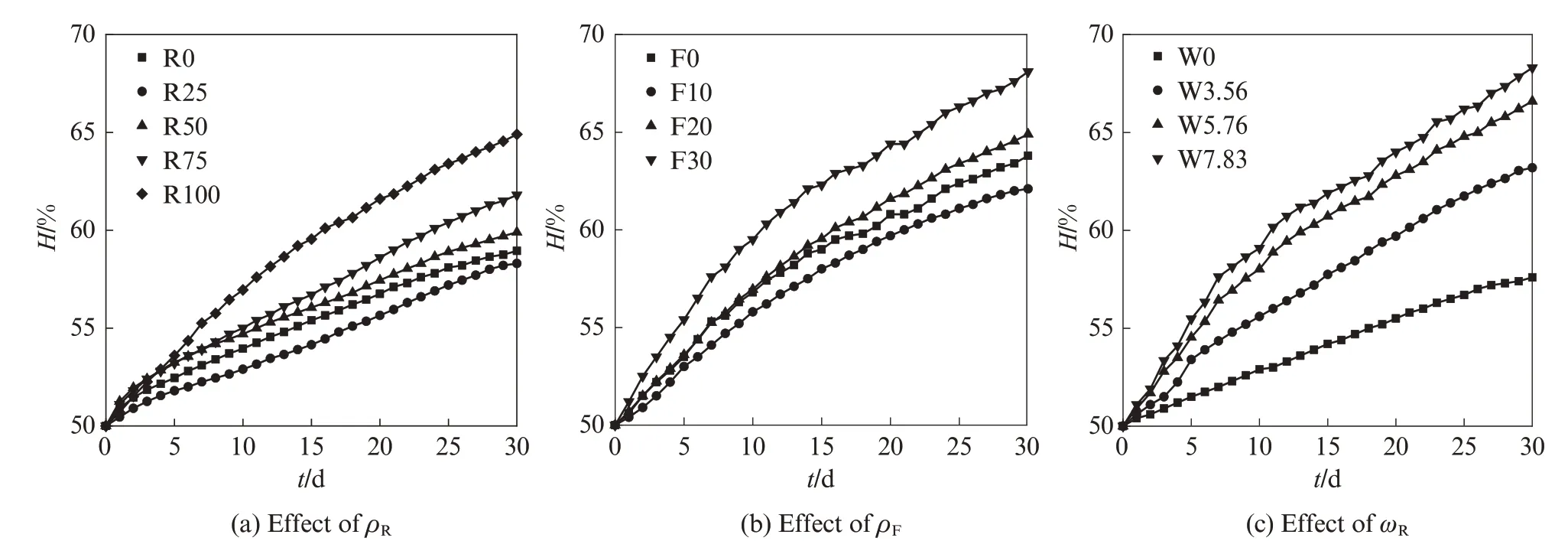
图6 混凝土内部湿度响应曲线Fig.6 Humidity response curves inside concrete

3.2 湿度响应速率

为进一步定量分析3 种因素对粉煤灰再生混凝土湿度响应的影响，定义湿度响应速率Δv=ΔH/t.ΔH为t时间内混凝土内部相对湿度变化量.3 种影响因素下混凝土湿度响应速率曲线如图7 所示.

由图7（a）可知：（1）混凝土的湿度响应速率随着ρR的增大呈先减小后增大的趋势.（2）当ρR小于25%时，混凝土湿度响应速率随ρR增大而减小；当ρR大于25%时，混凝土湿度响应速率随ρR的增大而增大.这是因为ρR较小时，再生粗骨料吸取部分拌和水，导致混凝土实际水胶比降低，混凝土内部结构变得致密；但是随着ρR的增大，其吸水量显著增大，影响水泥的水化进程；同时ρR的增大也会使混凝土内部原始损伤增大，导致混凝土内部孔隙率增大.湿度响应进行至5 d 时，ρR为0%、50%、75%和100%的混凝土试件较ρR为25%时分别增大了36.1%、80.6%、77.8%和94.4%；第30 d 时，分别增大7.6%、19.1%、41.8%和63.5%.由此可见，湿度响应的早期，再生粗骨料取代率对混凝土湿度响应的影响较大；随着湿度响应的进行，影响逐渐减小.

图7 混凝土湿度响应速率曲线Fig.7 Moisture response rate of concrete

由图7（b）可知：（1）随着ρF的增大，再生混凝土的湿度响应速率先减小后增大.（2）当ρF小于10%时，再生混凝土湿度响应速率随ρF的增大而减小；当ρF大于10%后，湿度响应速率随ρF的增大而增大.这主要因为粉煤灰作为活性掺和料可与水泥的水化产物Ca（OH）2进行二次水化，所生成的凝胶物质填充孔隙，使混凝土内部孔隙更为致密.10%的粉煤灰掺量会改善再生混凝土内部孔隙状态，延缓外界湿气渗入速率；当粉煤灰掺量超过10%后，粉煤灰等量取代水泥过多，使得混凝土中水化产物减少，混凝土平均孔径增加［15］.（3）当湿度响应进行至第5 d 时，ρF为0%、20%和30%的混凝土试件较ρF为10%时分别增大了16.7%、20.0%和80.0%；第30 d 时，分别增大15.0%、25.0%和50.0%.分析以上数据可知，在湿度响应的早期，粉煤灰掺量对混凝土湿度响应速率影响较大；且粉煤灰掺量越大，不同时段的湿度响应速率差异越明显.

由图7（c）可知：（1）再生混凝土的湿度响应速率随着ωR的增大而增大.一方面，这是因为再生粗骨料中的孔隙水在混凝土振捣过程中易析出，未及时水化的水分在骨料周边形成小水囊，影响混凝土的致密性；另一方面，由吸水性试验可知，随着ωR的增大，混凝土内部的孔隙结构逐渐变差，孔隙率逐渐增大.（2）湿度响应进行至第5 d 时，ωR为3.56%、5.76%和7.83%的混凝土试件湿度响应速率较ωR为0%的试件分别增大了106.7%、143.3%和166.7%；第30 d时，分别增大79.8%、100.0%和113.2%.由此表明，在湿度响应的早期，ωR对混凝土湿度响应速率的影响较大；且随着ωR的增加，不同时段的混凝土湿度响应速率差距增大.

4 粉煤灰再生混凝土湿度响应预测模型

4.1 表层混凝土湿气扩散系数

混凝土湿度响应试验结果表明，混凝土内部相对湿度随响应时间而变化，即混凝土内湿度传输可以归为非稳态扩散问题.于是，根据变值扩散系数情形下的扩散方程，得到混凝土湿气扩散系数（D）的计算表达式［13］：

式中：η称为Boltzmamn 变量（η=xt-0.5），当混凝土内部深度x一定时，其为时间t的函数；Hf代表响应时刻末混凝土内部相对湿度，%.

根据式（2）计算得到3 种影响因素下的再生混凝土湿气扩散系数随相对湿度的变化规律，如图8所示.

图8 混凝土湿气扩散系数演变规律Fig.8 Evolution law of moisture diffusion coefficient of concrete

由图8 可知，随着混凝土内部相对湿度的增加，3种影响因素下混凝土的湿气扩散系数（D）均逐渐减小.这是由于混凝土湿气传输的驱动力是混凝土内外湿度梯度，混凝土内部相对湿度增大，导致混凝土内外湿度梯度减小.混凝土内部相对湿度相同时，3种工况下的湿气扩散系数表现为：ρR为25%的混凝土D值最小，ρR为0%、50%、75%和100%的D值依次增大；ρF为10%的混凝土的D值最小，ρF为0%、20%和30%的D值依次增大；混凝土的D值随着ωR的增大而增大.

4.2 再生混凝土相对湿度响应预测模型

4.2.1 相对湿度响应理论模型

混凝土内的传质过程由Fick 第二定律决定.根据Fick 第二定律可获得混凝土内部任意时间、任意位置的相对湿度H（x，t），其表达式如式（3）所示［13］.

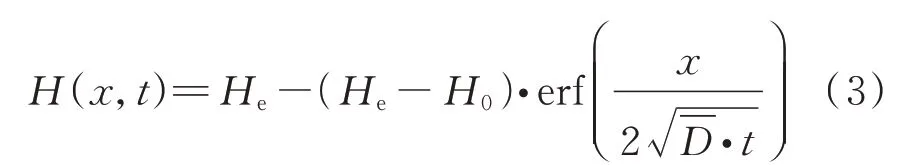
由式（3）可以看出，混凝土的等效湿气扩散系数对混凝土内部相对湿度响应的过程具有决定性的作用.因此，为确定再生混凝土内部相对湿度响应预测模型，应首先建立再生混凝土等效湿气扩散系数的计算模型.

4.2.2 再生混凝土等效湿气系数的计算模型

根据传质的相关理论，在同一个传质系统中，扩散系数和扩散时间的乘积为常数［13］.在混凝土湿度响应时间（0，t）内，对该时间段内的湿气扩散系数进行积分，并取平均值，即可得到等效湿度扩散系数，如式（4）所示.

利用式（4）及混凝土湿气扩散系数数据，计算得到不同再生骨料取代率、不同粉煤灰掺量和不同再生骨料初始含水率混凝土的等效湿气扩散系数，结果如图9 所示.

图9 混凝土等效湿气扩散系数Fig.9 Equivalent moisture diffusion coefficient of concrete

根据上述计算结果，将ρR、ρF和ωR作为影响混凝土湿气扩散系数的重要因素进行数值拟合，得到再生混凝土等效湿气扩散系数的预测模型公式，如式（5）所示.

4.2.3 湿度响应模型的验证

在混凝土内部相对湿度响应预测模型的验证过程中，式（3）中误差函数的计算可选用双曲正切函数的近似算法［13］，如式（6）所示.

以湿度响应过程R75 工况为例，介绍混凝土内部相对湿度的计算过程.混凝土水胶比为0.40，距混凝土表面深度x=0.05 m，混凝土内部实际初始相对湿度H0=50%，外界环境实际相对湿度He=90%，环境温度T=25 ℃，具体计算过程如下.

（1）首先，利用再生混凝土等效湿气扩散系数的预测模型（式（5））计算R75 的等效湿气扩散系数，其中ρR=75%、ρF=20%、ωR=4.5%.

（3）最后，将x=0.05 m、H0=50%、He=90%，以及不同时刻的误差函数值代入式（3），得到不同时刻的混凝土内部相对湿度的计算值.

将R75 工况的湿度响应试验值与计算值进行对比，如图10 所示.由图10 可知，以等效湿气扩散系数的计算模型为基础，采用双曲正切函数的近似算法计算误差函数，计算得到的再生混凝土内部相对湿度计算值与试验值的最大误差为4.65%，误差小于5%，表明计算结果与试验结果吻合较好，本文提出的再生混凝土相对湿度响应预测模型可行.