沥青路面结构粒料层非线性行为研究

黄优，刘朝晖，柳力，张健，李盛，张允宝,2

(1.长沙理工大学交通运输工程学院，湖南长沙，410114；2.湖南省交通运输厅建设造价管理站，湖南长沙，410011)

粒料层是沥青路面结构的重要组成部分，广泛应用于柔性基层、倒装复合式基层和底基层等路面结构中。柔性粒料基层沥青路面一直是欧美发达国家的主流路面结构形式。粒料层尤其是近几年发展起来的倒装复合式基层，具有能缓解沥青面层早期裂缝、透水性好等优点，在我国南方部分地区仍然应用较多。我国的沥青路面结构以半刚性基层为主，人们对粒料的材料特性和结构行为特征研究较少，因此，在工程应用中出现了一些与现有设计体系不相适应的情况，如粒料基层沥青路面的路表弯沉过大、难以通过验收等。郑健龙[1]提出了“结构层寿命分层递增”的设计理念，强调了下部结构的重要性和耐久性。

与半刚性材料不同，粒料具有典型的非线弹性特性(应力依赖性)，主要表现为回弹模量(Mr)随着围压增加而增加，随偏应力增加而减小[2-6]。为此，学者们提出了动态三轴试验方法以及各种应力依赖模型来表征动态回弹模量的应力依赖性[7-15]。我国JTG D50—2017“公路沥青路面设计规范”也引进了三参数应力依赖模型作为粒料动态回弹模量的预估模型[16]。该模型综合考虑了体应力和剪切应力的影响。粒料回弹模量的应力依赖性意味着粒料层的模量不是一个定值，而是随着荷载、结构组合、环境条件等变化而变化。在粒料层结构内部，存在一个非线性的模量分布，即距荷载作用点不同距离的位置，其应力不一样，对应的动态回弹模量也不尽相同。同时，我国的道路结构设计以层状弹性体系为理论基础，需要给粒料层选择单一的弹性模量(也称为当量弹性模量)。然而，在实际应用过程中，当量弹性模量的选取方法并不统一。美国的力学-经验设计指南(MEPDG)对粒料层指定了应力水平(围压35 kPa，偏压103 kPa)来计算粒料层的弹性模量并作为设计值[17]，我国JTG D50—2017采用动态回弹模量在加载应力序列中的平均值作为粒料层弹性模量的设计值[16]。也有研究采用基于路表弯沉等效、粒料层沿荷载中轴线上的模量平均值或者中点处模量作为弹性模量设计值[18-25]。尽管这些方法都考虑了粒料层非线性特性与层状弹性设计体系间存在的差异，但所得结论不一，所得到的当量弹性模量适用性不强。其中一个重要因素是忽略了路面结构组合的影响。在不同路面结构组合中，粒料层的应力存在差异，表现出来的结构行为特征必定不一样，其对应的当量弹性模量的选取也必不相同，因此，有必要针对不同结构组合的沥青路面粒料层结构非线性行为进行研究。本文以Uzan 三参数应力依赖模型为基础，编制了自定义材料子程序，采用有限元法开展沥青路面结构计算；结合我国国情，选取3 种典型的沥青路面结构组合(即柔性粒料基层、半刚性基层+粒料底基层、粒料层+半刚性层的复合基层)，并对采用不同当量模量的粒料层线性结构进行计算，揭示结构组合影响下粒料层非线性动态回弹模量的分布规律，对比分析不同结构组合下粒料层结构行为特征，探讨结构组合对路面结构响应的影响，并对当前常用的当量模量进行评价。研究成果可对我国的沥青路面设计提供参考，促进粒料在道路工程中的推广应用。

1 有限元模型建立及验证

1.1 有限元模型建立

采用有限元软件(FEAP)对路面结构进行分析。建立二维轴对称模型。模型边界条件为：路基底部固定；两侧采用滑动支座约束其法向位移。采用圆形荷载，荷载半径根据需要确定。本文中，在模型验证阶段模拟落锤式弯沉仪(FWD)荷载，取FWD 加载板半径为15 cm。在结构分析中，模拟单轮荷载，半径为10 cm，荷载为0.7 MPa。有限元模型尺寸和单元尺寸对计算精度和计算速率有较大影响。通过试算确定路面结构模型尺寸为：水平方向路基长度取9 m，深度方向路基厚度取5 m，其他结构层按实际厚度选取。采用四节点双线性轴对称实体单元，在靠近荷载的局部区域或者路面结构响应的关键部位进行网格加密。在水平方向上，在距离荷载20 cm内，单元格边长不超过2.0 cm；在20～45 cm内，单元格边长不超过3.0 cm；竖向上，沥青面层内单元高度不超过2.0 cm，粒料层内单元高度不超过2.5 cm；在路基顶往下50 cm内，单元高度不超过3.5 cm。在其他远离荷载区域，为了降低计算成本，选取较疏的网格。在非线性结构计算中，考虑结构的自重应力。

1.2 有限元模型验证

选取某试验路实体路面结构对有限元模型进行验证。路面结构为典型的三层柔性路面结构即沥青面层+粒料层基层+土基，各结构层的材料参数通过室内试验确定。沥青混合料的动态模量通过SPT(simple performance tester)获得，建立Sigmoid模型(见式(1))的沥青混合料动态模量主曲线(参数见表1)，以预测不同温度和荷载频率下的沥青面层模量。根据FWD试验时沥青面层温度和冲击荷载频率，预测沥青面层的模量约为4 620 MPa(见表2)。

表1 沥青面层动态模量模型参数Table 1 Parameters of dynamic modulus for asphalt layer

式中：E*为动态模量；tf为参考温度对应的加载时间；δ为动态模量下限值；α为动态模量上限值；β和γ为主曲线的形状参数。

在有限元模型验证过程中，为了尽可能与实际情况相符，粒料层和土基模量均使用Uzan 三参数非线性动态回弹模量模型表征(见式(2))，并基于FORTRAN编制非线性材料子程序。粒料层和土基的材料参数来自室内重复加载动态三轴试验，通过非线性拟合得到粒料层和路基的动态回弹模量预测模型。泊松比选取经验值。最终确定的FEAP有限元模型输入参数见表2。

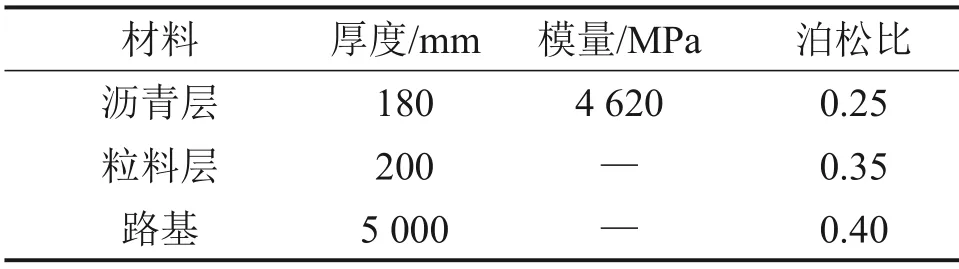
表2 FEAP有限元模型的路面结构和材料参数Table 2 Pavement structure and material parameters for FEAP finite element model

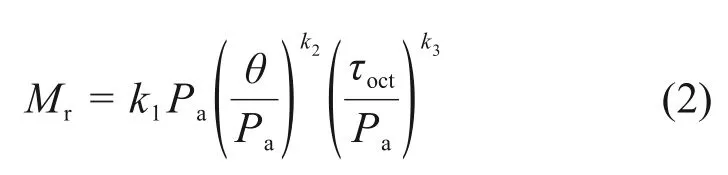
式中：θ为体应力；τoct为八面体剪切应力；Pa为标准大气压；k1，k2和k3为回归系数，对粒料层，k1=1 448，k2=0.657，k3=-0.017；对土基，k1=1 080，k2=0.167，k3=-0.044。

在试验路上进行FWD 落锤弯沉检测，每个点位进行四级加载，目标荷载分别为0.35，0.55，0.75和1.00 MPa，每级荷载重复4次。同时，将试验路的结构和材料参数、FWD 的加载参数输入FEAP有限元程序，计算其路表弯沉，并与实测弯沉进行比较，为方便说明，选取荷载0.55 MPa 的弯沉计算结果和实测结果，见图1。图1 中各点位的计算弯沉和实测弯沉均接近，绝大部分点位弯沉相对误差小于10%。使用FEAP有限元程序进行非线性结构计算得到弯沉和实测弯沉，两者较接近，说明有限元模型及材料子程序准确、合理。

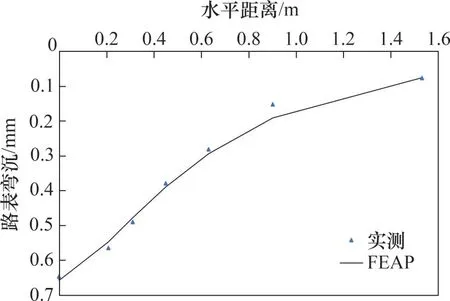
图1 实测弯沉与FEAP计算弯沉对比图Fig.1 Comparison of tested deflection basin and FEAP calculated deflection

2 粒料层结构行为分析

结合我国国情，选取3 种典型沥青路面结构(即柔性粒料基层沥青路面(柔性基层)、半刚性基层沥青路面(半刚性基层)和倒装复合式基层沥青路面(复合基层))同时进行非线性和线性结构分析，结果见图2。由于本文的研究重点是粒料层，为节省计算成本，对沥青面层的材料参数进行简化。根据沥青混合料的动态模量范围对沥青面层的模量进行合理假设，考察2 种不同刚度的沥青面层，模量E分别为1 000 MPa 和10 000 MPa。粒料层和土基材料参数见表2。泊松比按照经验参数进行选取，沥青面层、粒料层、半刚性层和路基的泊松比分别为0.25，0.35，0.20和0.40。结构参数和材料参数的选取参考JTG D50—2017“公路沥青路面设计规范”[16]和文献[19，26]。

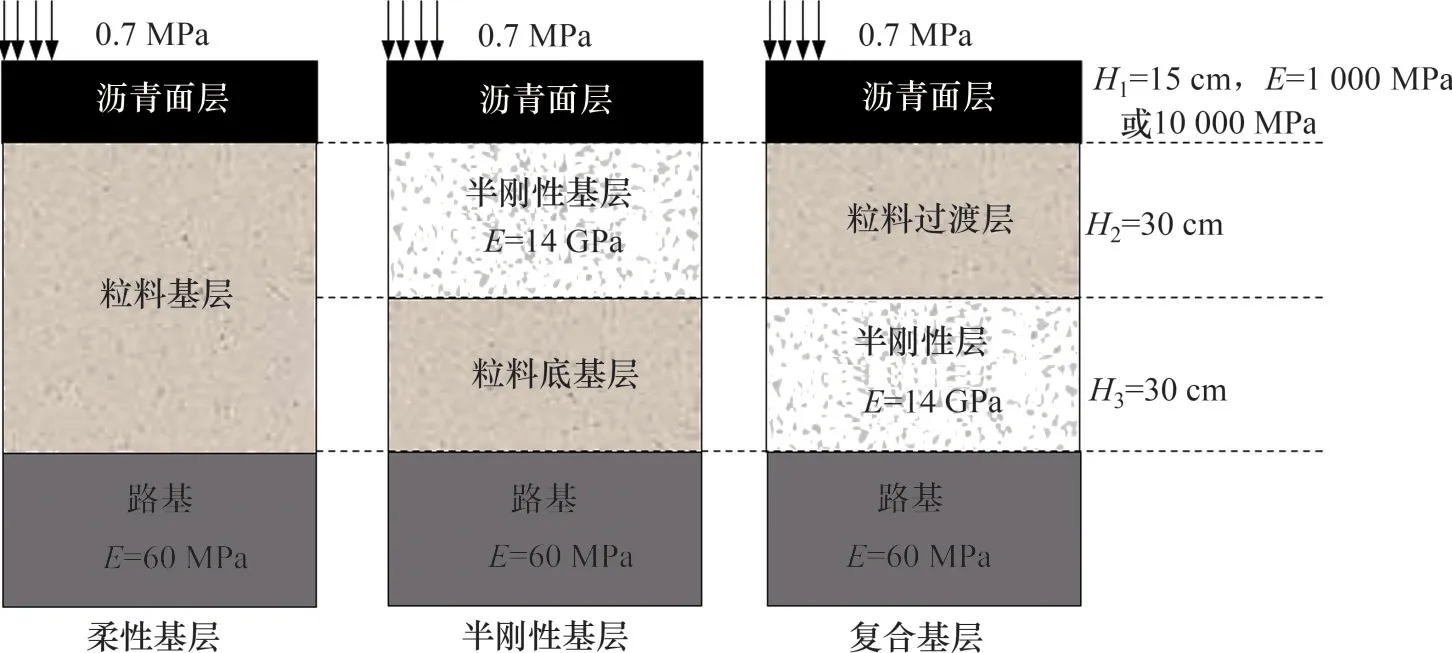
图2 3种含粒料层的典型沥青路面结构组合Fig.2 Three representative asphalt pavement structure combinations with granular layer

对3种典型路面结构分别开展非线性结构分析和线性结构分析。在非线性结构分析中，粒料层选用Uzan三参数非线性本构模型，见式(2)中粒料层参数k1，k2和k3。在线性结构分析中，粒料层模量根据不同的方法进行选取。目前，常见的几种粒料层当量模量选取方法如下。

1)平均值。选取粒料层沿荷载中轴线深度方向模量的平均值。

2)中点值。选取粒料层沿荷载中轴线深度方向中点的模量。

3) MEPDG 法[17]计算值。美国MEPDG 对粒料基层指定一个应力组合(围压35 kPa，偏压103 kPa)，将其代入式(2)，可算得粒料层模量为238 MPa。

4) JTG D50—2017 规范[16]计算值。我国JTG D50—2017“公路沥青路面设计规范”选取室内重复加载动态三轴回弹模量试验所得模量的平均值，通过实测实验数据计算，本文中所用粒料的模量平均值为268 MPa。

5)推荐值。美国MEPDG根据粒料分类及其物理参数确定模量推荐值[17]；我国JTG D50—2017也根据粒料种类推荐了粒料层的模量[16]。按照美国和中国的粒料分类法则，推荐的模量分别为276 MPa(美国)和300 MPa(中国)。

6)经验值。根据其他试验指标(比如加州承载比CBR 值)或者物理参数(级配、塑性指数、密度等)建立的经验公式推算弹性模量。

本文选择1)～5)的粒料层当量模量选取方法，具体模量见表3。

3 结果与讨论

设计3种路面结构、2种沥青面层模量。首先，采用Uzan 三参数模型对粒料层进行结构非线性计算；然后，分别选取表3中的当量模量进行线性结构计算；最后，将结构非线性计算与线性计算的路面结构行为进行比较分析，考察路表弯沉以及沥青面层底部最大水平应力、路基顶部压最大竖向应变、半刚性层底部最大水平应力等结构响应。

表3 不同取值方法的粒料层当量模量Table 3 Equivalent modulus of granular layer of different method MPa

为方便表述，可以认为结构非线性计算结果为“真实值”，并按照下式计算不同粒料层模量取法方法间结构响应的相对差：

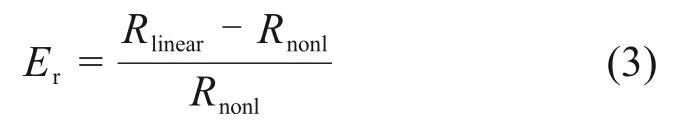
式中：Er为相对差；Rlinear为线性结构计算的路面结构响应参数，包括沥青面层底部最大拉应力、半刚性基层底部最大拉应力、土基顶部最大压应变；Rnonl为非线性结构计算的路面结构响应参数，包括沥青面层底部最大拉应力、半刚性基层底部最大拉应力和土基顶部最大压应变。

3.1 路表弯沉

根据FWD 传感器点位确定了9 个弯沉点位d1～d9，与荷载作用中心距离分别为0，0.20，0.30，0.45，0.60，0.90，1.20，1.50和1.80 m。提取路表不同点位的竖向变形得到3 种结构组合的路表弯沉。为便于观察，选取部分结果绘图进行比较分析，如图3 所示。图3 中，“实线”为柔性基层路面结构位移，“虚线”为复合基层路面结构位移，“空心点”为半刚性基层路面结构位移(以下同)。

图3 路表弯沉比较Fig.3 Comparison of surface deflection

从图3可以看到在相同荷载下，不同路面结构组合与不同当量模量下的路表弯沉差异显著，首先表现在最大弯沉不相同：在靠近荷载位置，柔性基层的路表弯沉最大，半刚性基层的路表弯沉最小，复合基层的路表弯沉介于这二者之间；沥青面层模量越小，最大弯沉则更大；而远离荷载之处如最远的弯沉d9处，不同路面结构和粒料层模量取值的路表弯沉均十分接近；复合基层结构的路表弯沉与半刚性基层结构的路表弯沉在第3～4个点位(450～600 mm)发生交叉(见图中红色虚线椭圆)。这是因为复合基层的半刚性层较深，因此，在较远的点位弯沉明显减小，而在靠近荷载区域由于有粒料层存在，路表弯沉又开始急剧增大；而在半刚性基层结构中，半刚性基层层位较浅，因此，路表弯沉减小处更靠近荷载区域，故弯沉曲线出现交叉。

路表弯沉的面积指数A是一个能更好地表征路面结构的整体承载能力的指标，A越小，说明路面结构承载能力越强，计算式为[27]

式中：A为弯沉面积指标；di为第i个点位路表弯沉。不同路面结构组合与不同当量模量的路表弯沉面积指标见图4。

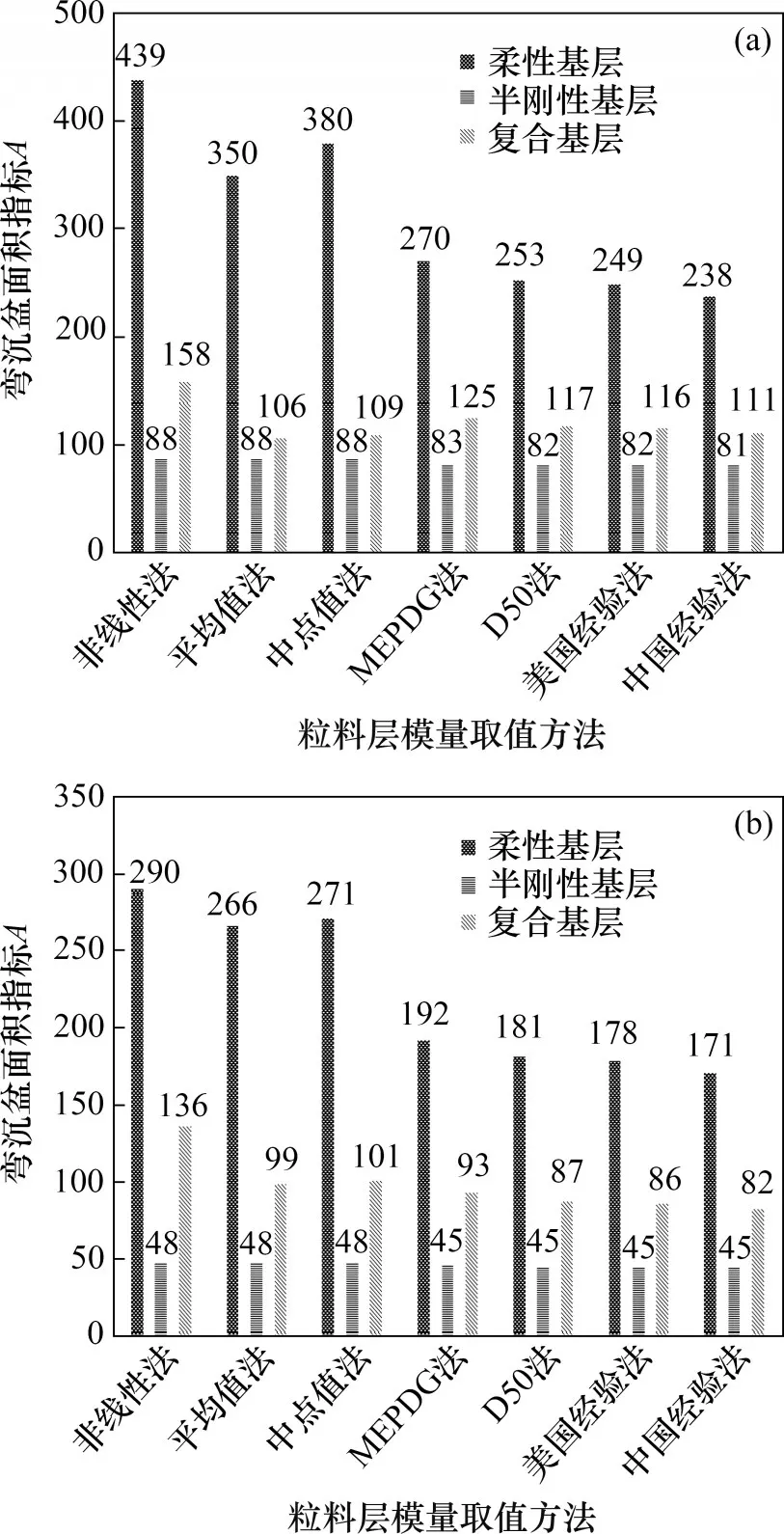
图4 不同路面结构组合与不同当量模量的路表弯沉面积指数AFig.4 A of different pavement structures for different granular layer modulus

从图4可见：柔性基层结构的路表弯沉面积指标A最大，复合式基层结构的A次之，半刚性基层结构的A最小，说明半刚性基层沥青路面的整体承载能力最强；柔性基层结构中粒料层不同当量模量(分别为1 000 MPa 和10 000 MPa)取值的弯沉面积指标A有着显著差异，采用非线性粒料层的路表弯沉面积A最大(分别为439和290)，平均值分别为350 和380，中点值分别为266 和271，均比较接近，其余当量弹性模量取值得到的A则更小，对应图3中柔性基层结构中各当量模量所得弯沉均小于非线性计算所得弯沉，尤其是采用规范或推荐的模量时。当前我国柔性基层沥青路面路表弯沉验收难以通过，这是因为我国的JTG D50—2017“公路沥青路面设计规范”的验收弯沉是基于层状弹性体系计算得到的，忽略了粒料层的非线性特性。根据本文研究，实际弯沉(考虑粒料非线性特性)均显著大于验收弯沉(根据现有规范模量取值进行线弹性计算)，因此容易出现“设计时满足要求，但现场验收不满足要求”的情况。复合基层不同粒料层模量取值方法的A也存在明显差异。半刚性基层的A最稳定，在81～88之间，说明半刚性基层的存在降低了路表弯沉对粒料层模量的敏感性。不同路面结构之间弯沉及其A的差异说明采用单一的弯沉验收标准存在不合理之处。

另一个值得关注的是路表弯沉走势。为了进一步考察弯沉随距离的变化情况，引入弯沉形状系数Fi，见式(5)。计算得到的F2～F8见图5。

观察图5发现：Fi越大，弯沉曲线越陡峭，说明对应的结构层越“薄弱”。以复合基层(图中虚线)为例，图5(a)中，由于面层和粒料层的模量都较小，因此，F2，F3和F4较大；结构层继续往下是半刚性层，模量突然增大，对应的F5和F6出现显著下降并进入稳定阶段；再往下进入路基，F7和F8缓慢增长。图5(b)中，由于沥青面层模量明显增大(E=10 000 MPa)，F2，F3和F4均较小。3 种路面结构中，半刚性基层的Fi整体最小，尤其是对应半刚性基层位置的F3和F4，而且不同粒料层当量模量取值方法之间几乎没有差别；复合基层的F2，F3和F4最大，说明半刚性下卧层的存在使得其上部的粒料层应力更加集中，反而增加了靠近荷载处路表弯沉的发展速率；而柔性基层结构的F5和F6(对应柔性基层部分)是最大的。可见，Fi能较好地反映出不同深度结构层的刚度，可以用来辅助判断结构层的模量或者损伤情况，这与文献[28]中的结论相同。

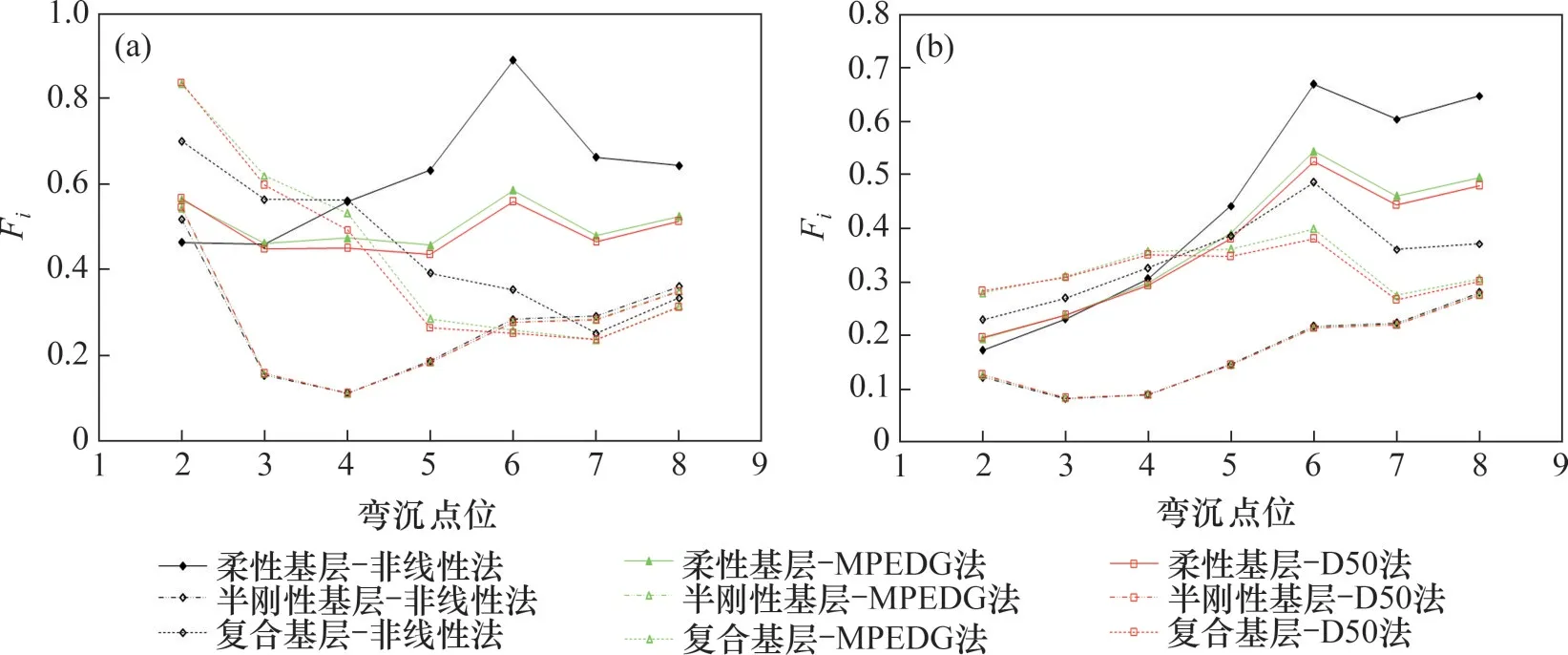
图5 路表弯沉形状因子FiFig.5 Shape factor Fi of surface deflection basin

3.2 粒料层模量分布

在相同荷载下，不同路面结构组合的路表弯沉存在差异，即路面结构组合的不同有可能造成结构层内部应力的差异。由于粒料层具有应力依赖性，因此，路面结构组合有可能对粒料层内部的模量分布产生影响。不同路面结构粒料层模量的非线性分布见图6和图7。

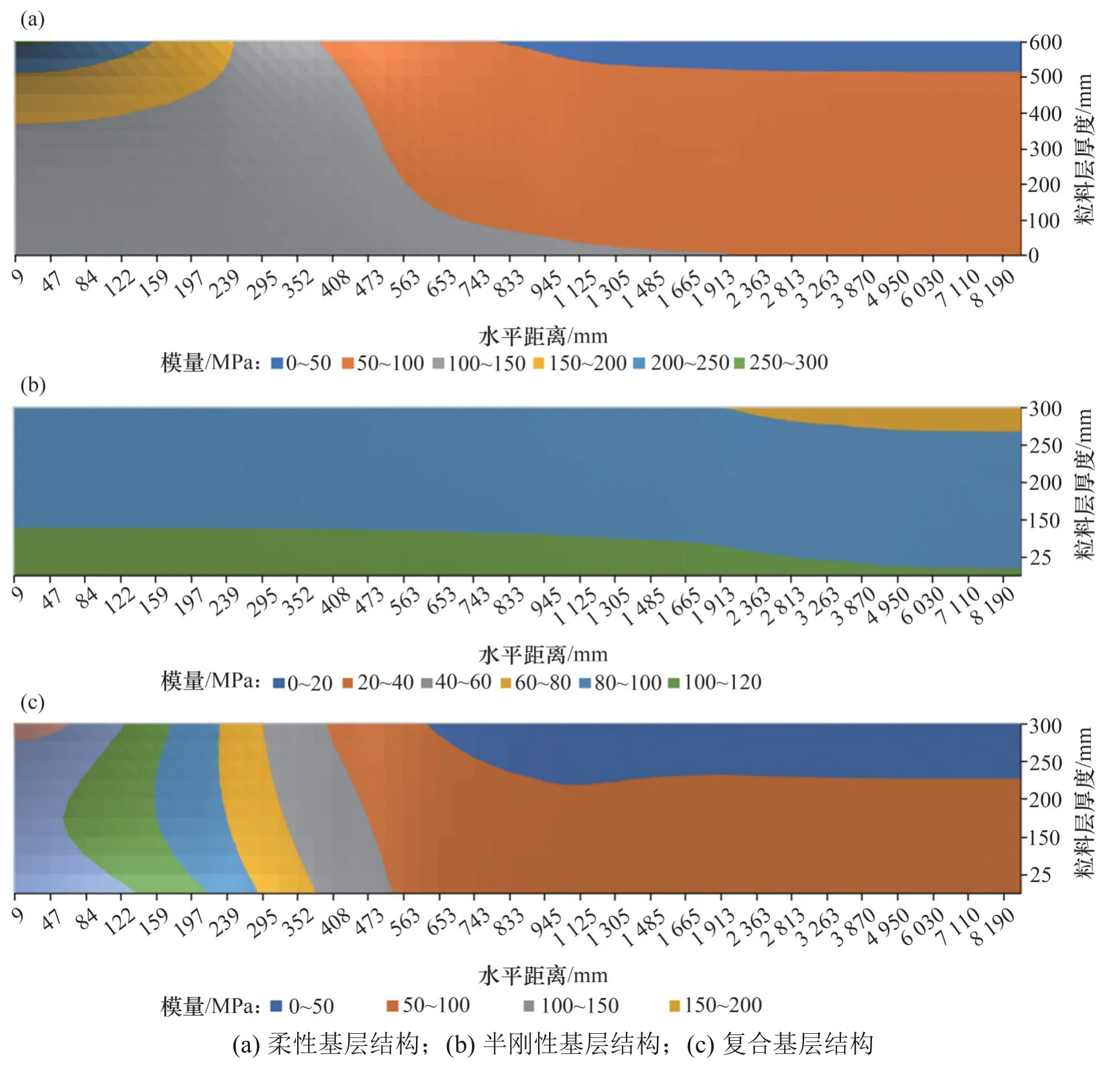
图6 粒料层非线性模量分布(E=1 000 MPa)Fig.6 Nonlinear modulus distribution of granular layer(E=1 000 MPa)

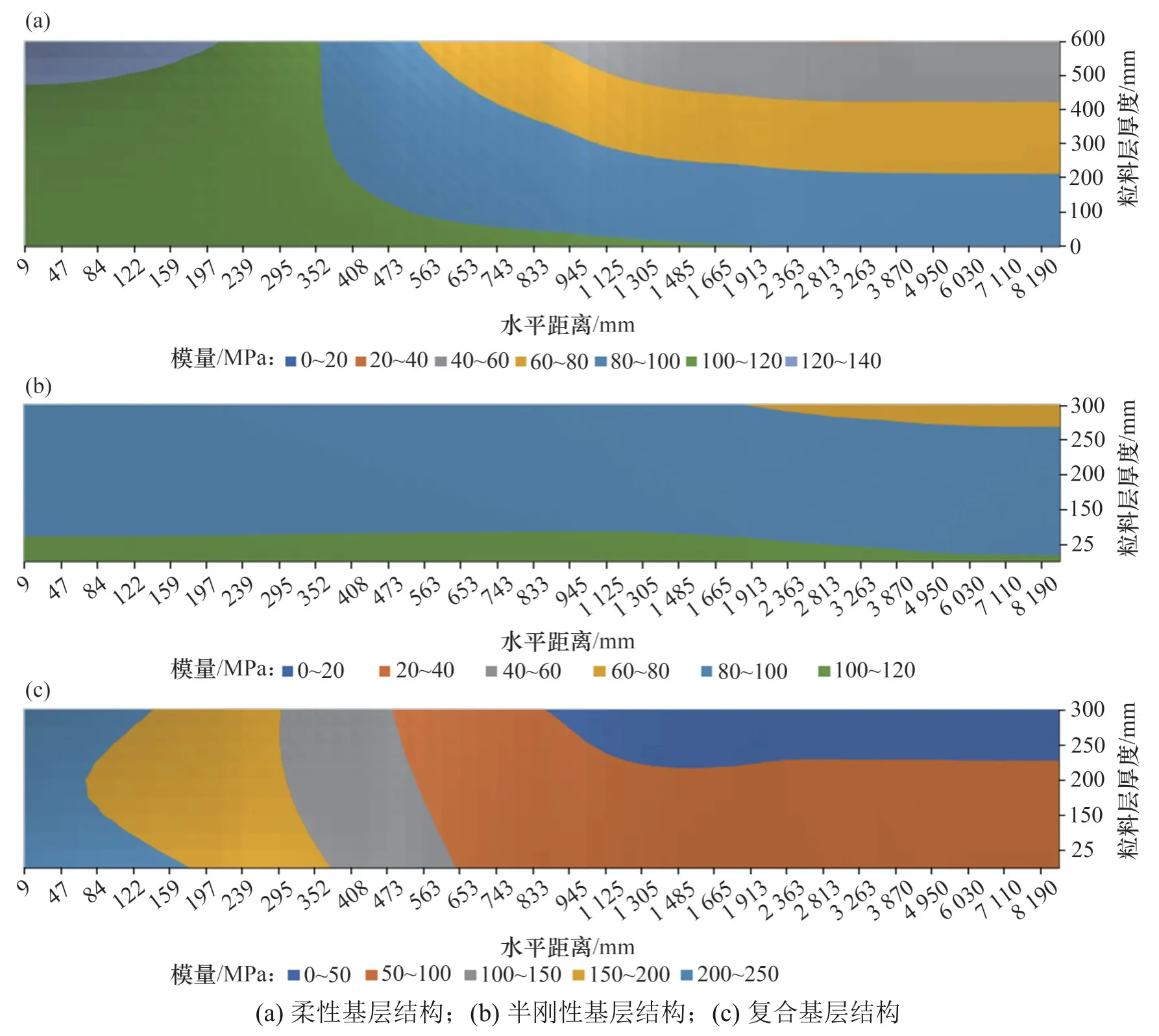
图7 粒料层非线性模量分布(E=10 000 MPa)Fig.7 Nonlinear modulus distribution of granular layer(E=10 000 MPa)

从图6和图7可知：在非线性计算中，由于粒料应力存在依赖性，粒料层的模量随着距荷载位置的距离不同而不同；在靠近荷载处，粒料层荷载应力较高，粒料层的模量较大；远离荷载处，粒料层荷载应力较低，粒料层的模量也较小。不同的结构组合中粒料层的模量分布范围及变化梯度差异显著，沥青面层刚度、半刚性基层的位置等都会影响粒料层模量的非线性分布。半刚性基层下的粒料层模量整体最小，模量分布范围最窄，模量变化梯度最小；而复合基层中(尤其沥青面层刚度小时，E=1 000 MPa)，粒料层模量整体水平最大，模量分布范围最广，模量变化梯度最大：在靠近荷载之处，模量达到350～400 MPa，而在远离荷载之处，模量低于50 MPa，相差超过7倍。此外，复合基层中，粒料层模量的梯度变化沿着水平方向变化较明显，而柔性路面结构中，粒料层模量梯度沿水平和深度方向均有变化。

表4列举了不同路面结构中粒料层的模量平均值和中点值。总体来讲，这2种取值方法得到的模量值比较接近，在绝大部分情况下，两者之间的相对差均小于10%。复合基层中粒料层的模量平均值(中点值)最大，约为粒料基层的2.0 倍，约为半刚性基层下粒料层的3.5倍，说明不同路面结构中，粒料层所表现出来的整体刚度差异非常大，在进行粒料层设计时，必须考虑结构因素的影响，合理选取模量。目前的设计规范无论是美国MEPDG 设计指南还是我国的JTG D50—2017设计规范，都只考虑了粒料层材料的非线性特性，而没有综合考虑路面结构的影响。

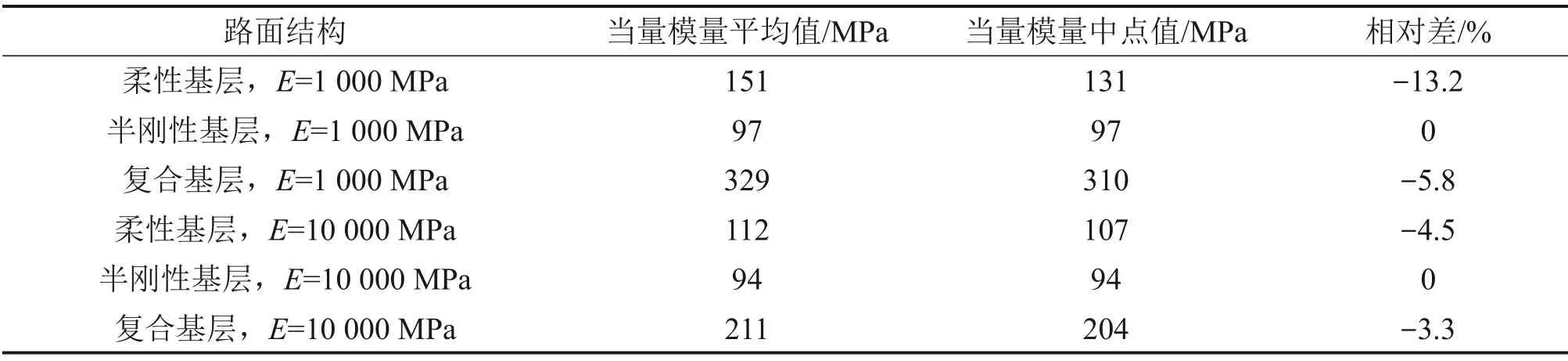
表4 平均值法和中点值法的当量模量比较Table 4 Equivalent modulus of mean value method and middle value method

3.3 路面结构关键响应

路面结构设计的核心问题是通过结构组合与材料比选将关键结构响应控制在容许范围内，以满足使用功能和服役寿命的要求。荷载作用中心点处的沥青面层底部水平应力、半刚性基层底部水平应力、路基顶部竖向应变等关键结构响应见图8～10。

3.3.1 沥青面底部水平压力

图8所示为沥青面层层底的水平应力状况。从图8(a)可见：沥青面层层底受力状况受基层的刚度影响很大；在柔性基层和复合基层结构中，位于沥青面层下部的是粒料层，模量较小，沥青面层底部均处于受拉状态(图中应力为负时，表示受拉，反之受压)；而半刚性基层结构中，沥青面层底部始终处于受压状态。从图8(b)可见：柔性基层路面结构(面层E=1 000 MPa)中，与粒料层非线性计算相比，平均值法和中点值法所得沥青底部拉应力分别增大了约14.1%和26.9%，其他各当量模量取值方法均显著减小(相对差为-24.6%～-42.4%)；在复合基层路面结构中，与粒料层非线性计算值相比，最接近的是我国JTG D50—2017 设计方法采用的当量模量(相对差为-0.61%)，其次是MEPDG美国经验法的弹性模量取值(相对差为-3.7%)，平均值法和中点值法所得值相对差最大(分别为-21.8%和-15.8%)。这是因为复合基层中的应力较高，粒料层表现出来的刚度也较大(见图6 和图7)，而我国的JTG D50—2017 设计规范模量和美国MEDPG设计指南的模量均较大(见表3)，因此，计算结果更为接近。而设置了半刚性基层后，沥青面层底部变为受压且不同模量取值方法之间的差异很小，说明在设置了半刚性基层后，不仅改善了沥青层的受力状况(转拉为压)，而且降低了沥青面层结构响应对粒料层模量取值方法的敏感性。

图8 沥青面层底部水平应力及相对差Fig.8 Horizontal stress and relative error at the bottom of asphalt layer

3.3.2 路基顶部应变

图9所示为路基顶部的最大竖向压应变。从图9可以看到：柔性基层路面结构中的路基顶部压应变最大；当面层刚度较低时(E=1 000 MPa)，路基顶部压应变受粒料层模量取值方法的影响较明显；当采用平均值和中点值时，路基顶部压应变与真实值相对差较小，分别约为-15%和-12%；但其他模量取值方法得到的路基顶部压应变相对差较大，为-31%～-34%；当面层模量较大时(E=10 000 MPa)，路基顶部压应变与真实值之间的差距略减小，平均值或中点值法所得压应变与真实值的相对差约为-5%；其他模量取值方法为-16%～-21%。设置了半刚性层后，路基顶部压应变显著减小，但不同粒料层当量弹性模量取值方法得到的路基顶部压应变之间仍然有一定差异：复合基层结构的相对差为-15%～-18%；而半刚性基层结构中平均值法和中点值法所得模量与真实值间非常接近(相对差为0.3%)，其他当量模量取值法与真实值间的相对差约为7%。这也说明半刚性层的存在一方面降低了路基顶部的最大压应变，同时降低了路基顶部压应变对粒料层模量取值方法的敏感性。

图9 路基顶部应变及相对差Fig.9 Vertical strain and relative error at the top of subgrade

对比图8 和图9 发现：在柔性基层路面结构中，使用平均值法或中点值法尽管增加了沥青路面底部水平应力，但降低了路基顶部的竖向压应变。这是因为在柔性基层结构中，粒料模量受应力水平影响，其模量随着深度增加而减小(见图6和图7)，而这2种方法的模量取值都介于粒料层非线性模量最大值与最小值之间。因此，在沥青面层底部(粒料层顶部)，这2 种方法低估了粒料层的模量，从而增加了沥青路面底部水平应力；而在路基顶部(粒料层底部)，这2 种方法高估了粒料层模量，从而降低了路基顶部的竖向压应变。这种由于粒料层模量非线性分布，其对不同路面结构响应的影响很难通过路表弯沉反映出来。

3.3.3 半刚性底部水平应力

半刚性层起到了提高路面结构整体刚度、降低应力水平的作用，同时降低了粒料层模量取值对关键路面结构响应的影响，但作为主要承力结构层，其本身也可能受到粒料层模量取值的影响，见图10。现有设计中的当量模量取值方法使半刚性基层底部拉应力降低约8%(沥青面层模量E=1 000 MPa)和约6%(沥青面层模量E=10 000 MPa)，使复合基层中半刚性基层底部拉应力降低约12%(沥青面层模量E=1 000 MPa)和约16%(沥青面层模量E=10 000 MPa)。此外，由于半刚性层的层位较低，复合基层中半刚性层底部拉应力比半刚性基层小30%～40%，因此，复合基层中半刚性层的受力状况更加有利。

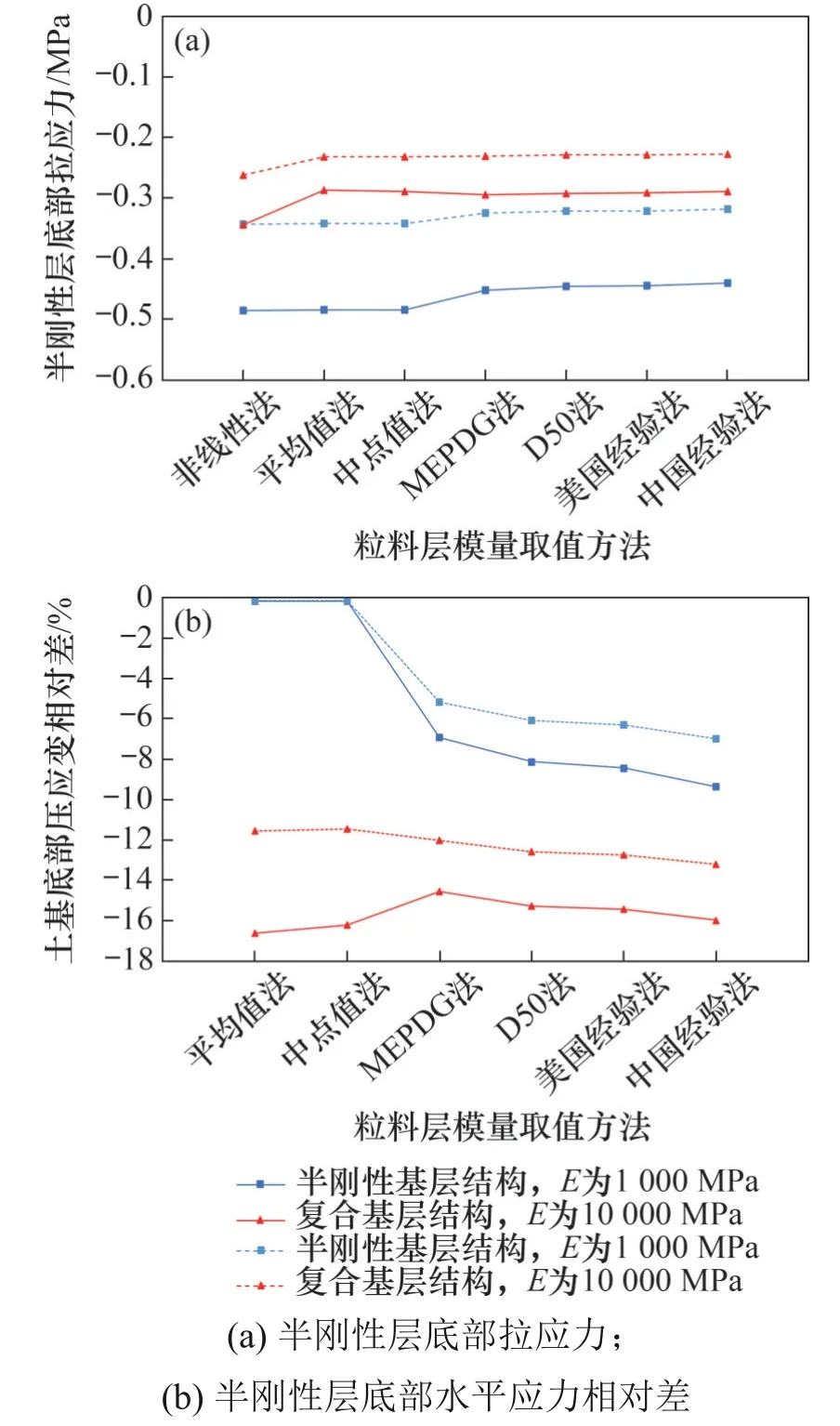
图10 半刚性层底部水平应力及相对差Fig.10 Horizontal stress and relative error at the bottom of semi-rigid layer

4 结论

1)柔性基层沥青路面的路表弯沉最大，整体变化趋势较陡，受粒料层模量选取方法的影响较大；半刚性基层沥青路面的路表弯沉最小，受粒料层模量选取方法的影响最小；复合基层沥青路面的路表弯沉介于两者之间，但靠近荷载区域的弯沉变化最大。路表弯沉的形状系数Fi与结构层刚度有较好的对应关系，可以用于辅助评价内部结构层的模量和损坏状况。

2) 半刚性基层结构的路表弯沉与柔性基层、复合基层结构的路表弯沉差异显著。考虑粒料的非线性时，路表弯沉会更大，因此，当采用规范的当量模量取值方法进行设计时，会低估路面结构的路表弯沉(尤其是柔性基层结构)。对不同路面结构采用单一弯沉验收标准存在不合理之处。

3)靠近荷载区域粒料层模量较大，远离荷载区粒料层模量减小。粒料层模量的整体水平、分布范围和变化梯度均受结构组合的影响，其中复合基层结构的粒料层模量整体最大、分布范围最广且变化梯度最明显，模量最大值和最小值之间相差可达7倍；半刚性基层结构中粒料层模量、分布范围和变化梯度均最小。不同路面结构粒料层表现出来的刚度差异非常大：复合基层结构中粒料层模量均值约为柔性基层结构中粒料层模量的2.0 倍，约为半刚性基层结构中粒料底基层模量的3.5倍。

4)绝大部分的当量模量均取值过高，从而有低估路面结构响应的风险。沥青面层底部拉应力和路基顶部压应变在柔性基层结构中最多被低估了约40%和34%，在复合基层结构中，拉应力和路基顶部压应变分别为22%和18%；半刚性层底部水平拉应力在复合基层结构和半刚性基层结构中分别最多被低估了约16%和8%。

5)目前对粒料层当量模量选取仍缺乏行之有效的方法，应该综合考虑非线性材料特性与路面结构组合的影响，提出更合理的当量模量取值法则。