黏土地基中自平衡试桩Q-s曲线解析转换方法及模型试验研究

欧孝夺，白露，吕政凡，江杰，李胜

(1.广西大学土木建筑工程学院，广西南宁，530004；2.工程防灾与结构安全教育部重点实验室，广西南宁，530004；3.广西金属尾矿安全防控工程技术研究中心，广西南宁，530004；4.同济大学土木工程学院，上海，200092)

自平衡试桩法作为一种新的基桩承载力测试方法，与传统的堆载法、锚桩法相比，它不需要压重平台或锚桩反力装置，测试可节省时间、人力、费用，近年来被广泛应用于实际工程中确定单桩极限承载力[1-3]。国内外学者对自平衡试桩静载荷试验及应用进行了大量研究，OSTERBERG[4]于1989年用自平衡试桩试验对单桩承载力进行研究，之后在欧洲及日本等地区得到广泛应用。我国龚维明等[5-6]将此法在国内开始推广与实际应用，并制定相应规范[7]。

目前，工程中将自平衡试桩测试结果转换为传统静压试验Q-s曲线的方法主要为简化转换法和精确转换法。对于简化转换法行业规范[8]并未对转换系数有较准确取值，且相关理论并不完善[9]；而精确转换法则需要实测桩身加载的各微段轴力，增加了试桩的工作量。因此，对自平衡试桩法的荷载传递机理进行深入研究，求解一种理论解析转换方法用于自平衡测试确定单桩承载力具有重要意义。熊巨华等[10-11]对桩侧土、桩端土分别采用双折线、三折线模型并利用荷载传递模型推导出自平衡试桩的一种解析转换解，但未考虑上段桩自重抵抗桩端加载的影响。SEOL[12-13]在Mindlin解的基础上，提出一种考虑耦合侧摩阻力的荷载传递方法，对桩土界面的滑移和剪切荷载传递进行研究，而对转换方法并没有进行深入研究。奚笑舟等[14]假定桩侧土符合三折线模型对自平衡试桩上段桩荷载-位移理论解析进行推导，拟合试验数据得到传递函数的相关参数，该法并未对下段桩荷载传递以及具体转换方法进行推导研究。综上所述，国内外对自平衡试桩理论研究仍有待进一步研究完善。

国内外对桩土非线性接触模型的研究表明，用双曲线模型可以较好地模拟桩土荷载传递[15]，但由于双曲线函数求解微分方程比较困难，通常将其假定为折线模型，ZHANG 等[16]采用双曲线模型模拟桩土传递函数，以双折线的模型模描述桩端硬化情况，求解出单桩的承载特性弹塑性解。而贺志军等[17-18]通过大量模型试验发现桩周土界面侧摩阻力与相对位移的规律可用分段函数表示，并指出侧摩阻力随着相对位移增加至极限值后逐渐减小趋于稳定。肖宏彬[19]通过对大量桩侧摩阻力测试及静载试验得出，硬黏土、结构性黏土层随着相对位移增大桩侧摩阻力达到峰值后会出现软化而趋于稳定，表明黏土地基中桩侧摩阻力有明显的软化特征。

本文作者假定桩侧荷载传递模型为软化三折线模型，桩端土符合弹-塑性模型，考虑上段桩自重的影响，利用荷载传递法进行推导上、下段桩Q-s曲线弹塑性发展规律的解析解，由自平衡测试结果拟合得到荷载传递函数相关模型参数，代入上述解析公式中，将其转换为传统静压试验荷载-位移曲线，得到试桩极限承载力。最后设置传统静压桩和自平衡试桩两组室内模型对比试验，将本文转换方法与传统静压试验结果、简化转换法和精确转换法结果进行对比，对本文方法进行验证，并对该法实用性进行分析。

1 自平衡试桩法基本原理

自平衡法是通过在桩底或桩身平衡点位置预先埋置荷载箱，利用油泵对荷载箱施压，使荷载箱对上、下段桩产生相应的推力，从而在上段桩侧与土体形成负摩阻力，下段桩侧摩阻力和端承力也开始发挥作用，对荷载箱加压直至桩破坏，其作用机理如图1所示。图1中，G为上段桩自重，su和sv分别为上、下段桩底的位移，Qu为荷载箱的加载。

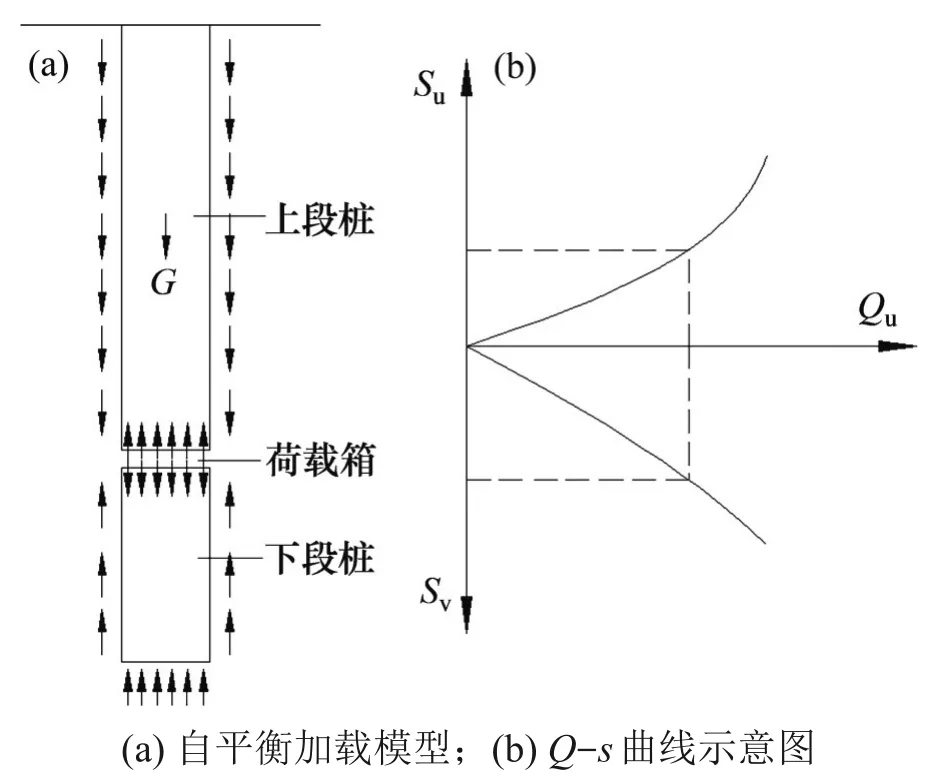
图1 自平衡试桩法原理示意图Fig.1 Schematic diagram of self-balanced test pile

1.1 荷载传递函数基本微分方程

荷载传递法是将桩看作n个弹性微小单元组成，各单元与土体之间的摩阻力作用均采用非线性弹簧表示，如图2 所示。图2 中，s(z)为桩身相对位移，q(z)为桩侧摩阻力，ΔLi为桩微段的长度。

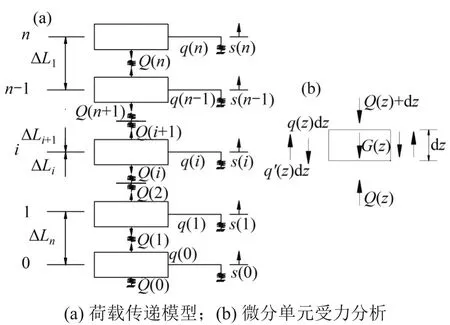
图2 桩土相互作用及荷载传递计算模型Fig.2 Calculation models of pile soil interaction and load transfer

由微分单元受力可得

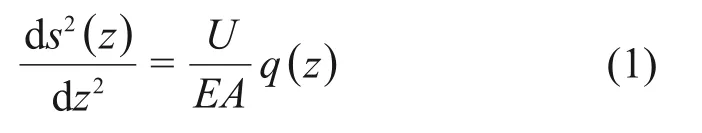
式中：U为桩周长；E和A分别为桩的弹性模量和横截面积。根据剪切位移法有

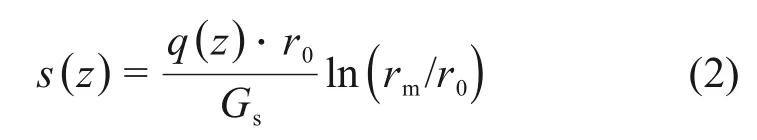
式中：r0为桩半径；rm为有效影响半径，在径向距离rm以外的土体剪切变形可忽略不计，rm=χ1χ2L1(1-νs)，χ1和χ2为土体不均匀程度经验系数[20]；Gs为桩侧土剪切模量；vs为土体泊松比。

将式(2)代入式(1)可得

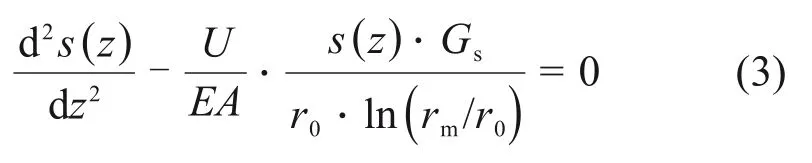
令k=k定义为桩土剪切刚度系数，可得

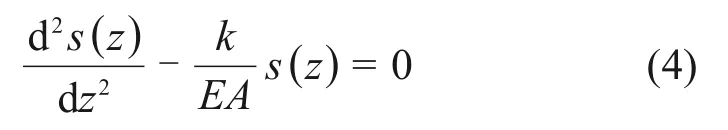
1.2 桩-土荷载传递函数

假定桩-土界面的侧摩阻力与桩土相对位移之间的关系符合软化折线模型，桩端土符合双折线模型，如图3 所示。图3 中，s为桩土界面相对位移，k1,3为上、下段桩土弹性阶段剪切刚度系数，k2,4为上、下段桩土塑性软化阶段剪切刚度系数，sa,c为上、下段桩土界面弹性极限位移，sb为上段桩塑性软化阶段极限位移，k5与k6为下段桩端抗压刚度系数，se为桩端弹性极限位移。

图3 桩土荷载传递函数模型Fig.3 Pile soil load transfer function model

采用荷载传递函数表达如下：

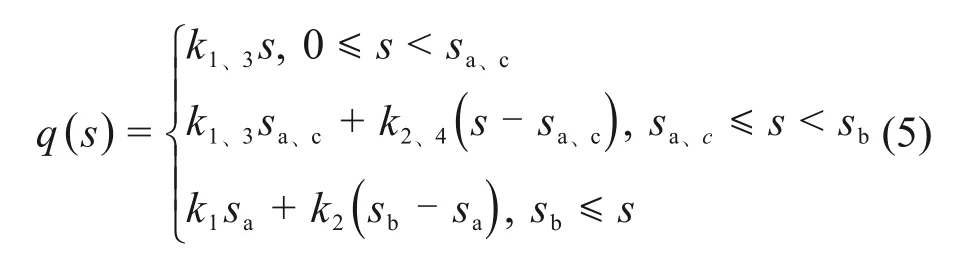
当上段桩土相对位移s处于0～sa之间时为弹性阶段，随着负摩阻力增大，相对位移在sa～sb为塑性软化阶段，当相对位移大于sb时，桩周土体处于理想塑性阶段。对于下段桩，相对位移s处于0～sc之间为弹性阶段，当相对位移大于sc时为塑性软化阶段。

2 Q-s曲线解析理论推导

2.1 上段桩荷载传递规律

由于自平衡试验上段桩身自重一定程度上抵抗桩端加载，因此，对试桩微元平衡推导时应计入重力的影响，可得上段桩侧荷载传递基本微分方程：

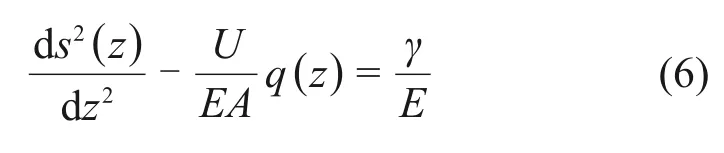
式中：γ为桩体重度。

无论桩土荷载传递发展处于何种阶段，均满足以下边界条件。

上段桩顶时，

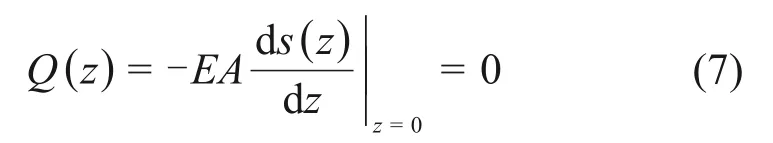
上段桩底时，

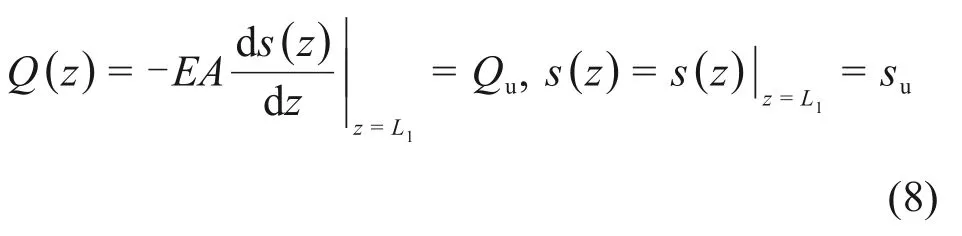
式中：Qu和su分别为荷载箱向上的加载及位移。

1)当桩侧土处于全弹性状态时，将桩侧传递函数(5)代入式(6)，令=αiL1(其中，i=1，2；L1为上段桩长)；可得微分方程：

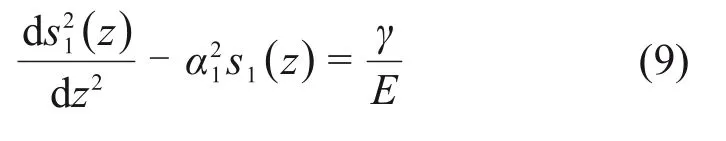
解得：

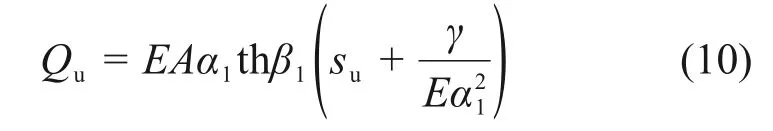
2)当桩侧土处于弹性、塑性软化共存状态时，若桩侧土体发展出现塑性软化特征，即k2＜0，表示随着相对位移的增加，桩侧摩阻力逐渐减小，此时，令代入荷载传递函数得微分方程：

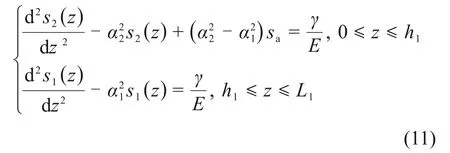
式中：h1为上段桩塑性区开展长度。

此时，有连续条件：

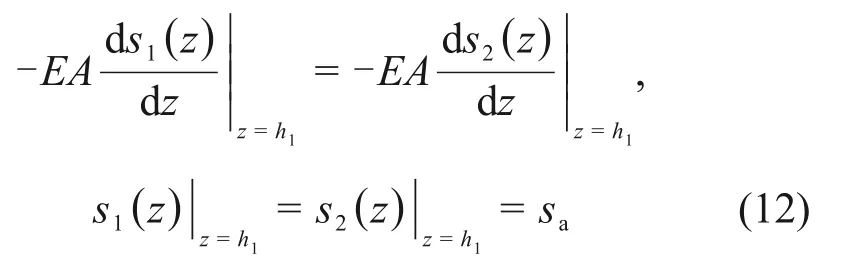
解得

Qu和su随着塑性区h1的开展，可得Q-s曲线。此外，有

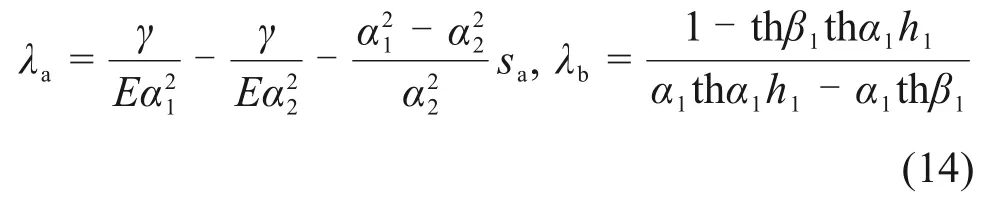
3)当桩侧土处于塑性软化状态时，有

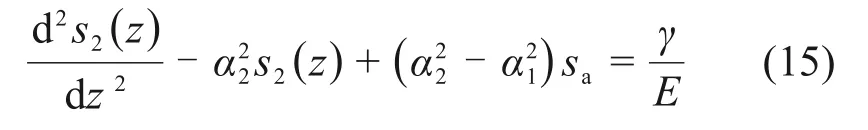
解得：

4)当桩侧土处于塑性软化、理想塑性共存状态时，有

连续条件为

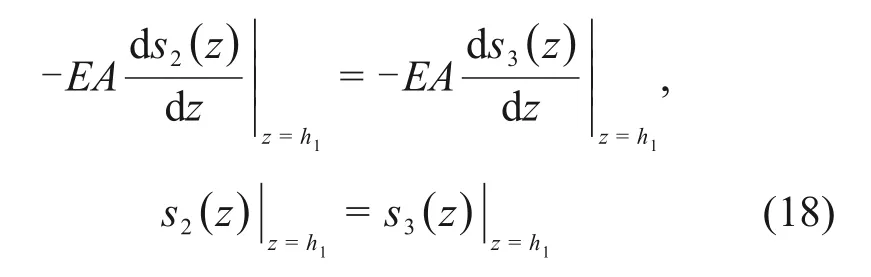
解得：

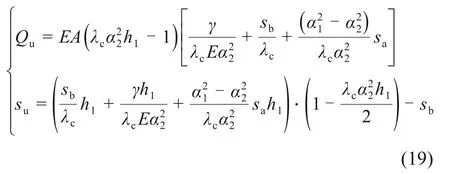
式中：

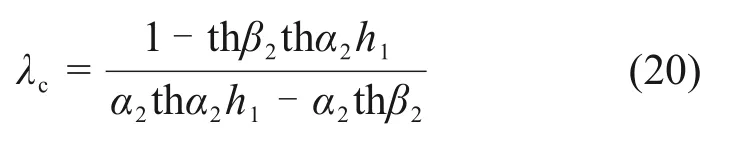
5)当桩侧土处于理想塑性状态时，有

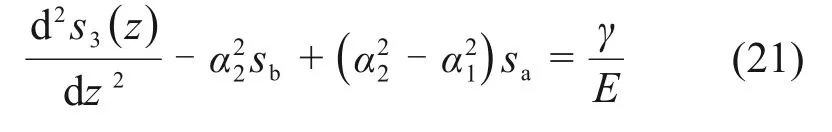
解得

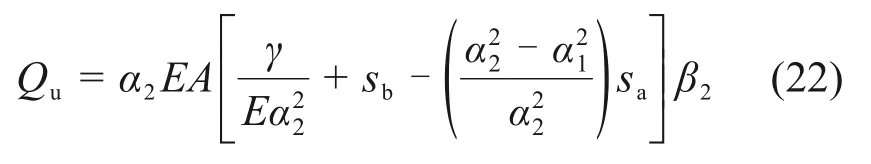
2.2 下段桩解析转换法

由于自平衡法试桩下段桩和传统受压桩受力相同，下段桩微元受力分析可不考虑重力的影响。当荷载箱施加相同的压力时，下段桩相对变形较小。假定下段桩桩侧土荷载传递符合软化双折线模型，同时假定桩侧土先于桩端土进入塑性阶段[10]。

1)下段桩侧土处于弹性，桩端土也处于弹性状态。

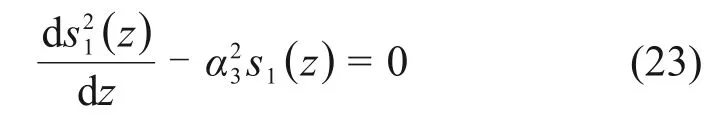
边界条件为

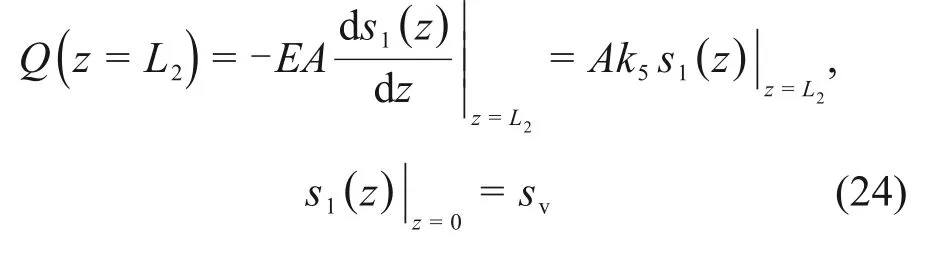
解得

式中：Qv和sv分别为下段桩加载的荷载及位移。

2)下段桩侧土处于弹性、塑性软化共存状态，桩端土也处于弹性状态。

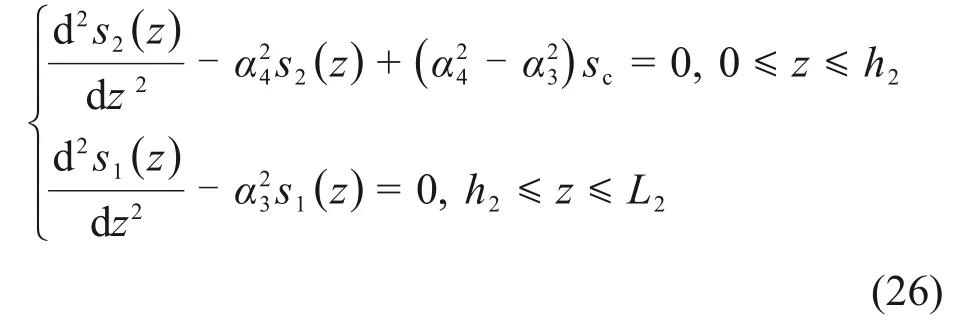
式中：h2为下段桩塑性区开展长度。

边界条件为

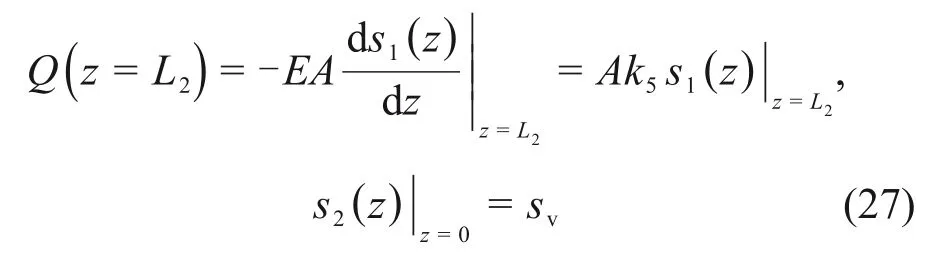
连续条件为

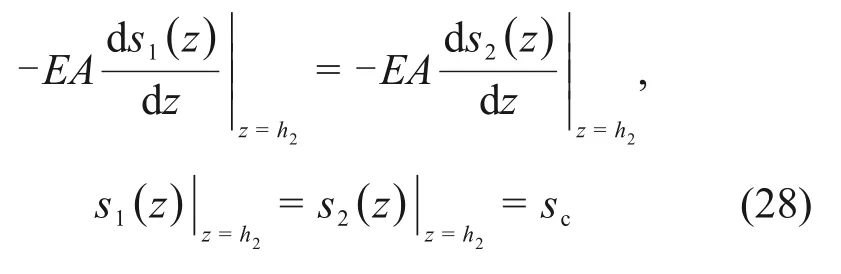
解得

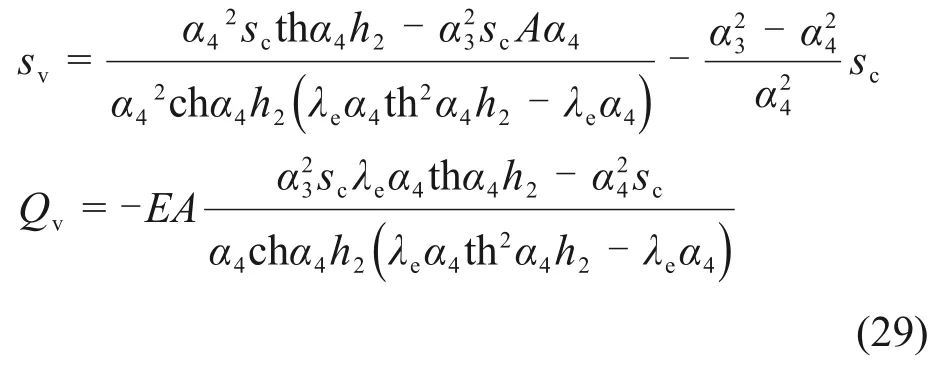
式中：

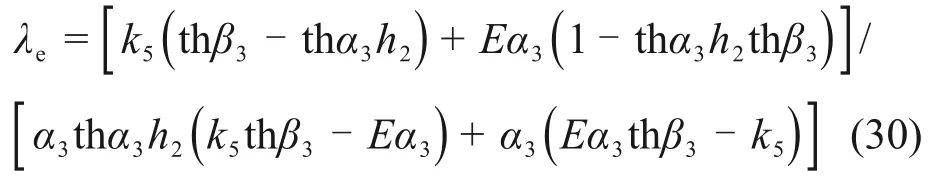
3)下段桩侧土处于塑性软化状态，桩端土仍处于弹性状态。

边界条件为

解得

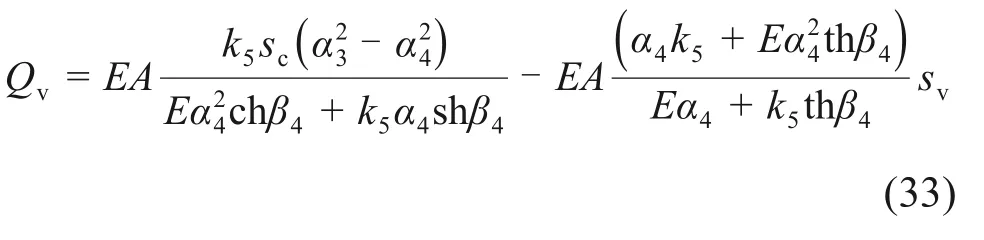
4)下段桩侧土仍处于塑性软化状态，桩端土处于临界塑性状态。

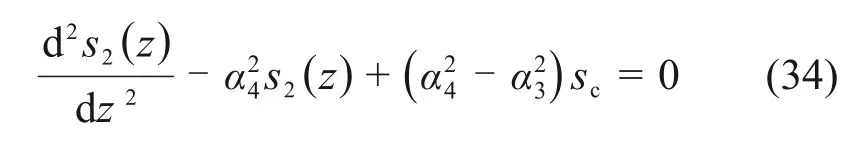
边界条件为

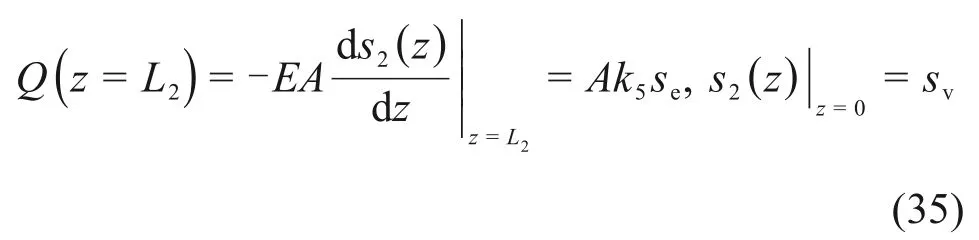
解得

5)下段桩侧土仍处于塑性软化状态，桩端土处于塑性状态。

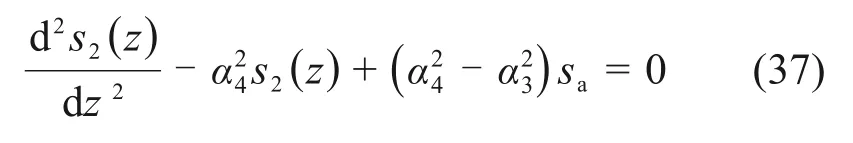
边界条件为

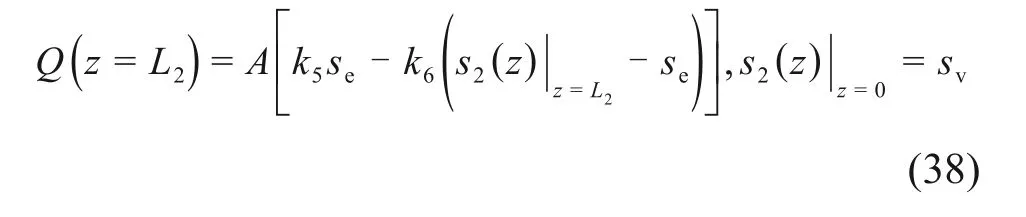
解得

若对于其他土质，当拟合不存在塑性软化阶段即k2和k4均为0时，直接进入理想塑性阶段解析公式计算，可求解相应的sv和Qv。

3 模型参数确定及转换方法

3.1 模型参数确定

在均质土层中，自平衡试桩解析公式中模型参数共有10 个。对于上段桩，桩侧摩阻力发展主要有弹性阶段、塑性软化阶段、理想塑性阶段，依据实测结果按式(10)和(13)可得到上段桩模型参数。对于下段桩端土抗压刚度系数k5，可根据RANDOLPH 等[20]对弹性半空间基础解确定初值，其桩侧摩阻力塑性发展主要经过桩侧弹性阶段、塑性软化阶段、桩侧塑性软化桩端弹性阶段、桩侧塑性软化桩端塑性阶段，可依据式(40)计算k5初值，另外，根据加载实测结果按式(25)和(29)得到下段桩侧模型参数。

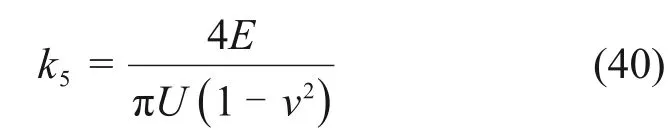
式中：E为桩端土层的弹性模量；v为桩端土泊松比。

3.2 转换方法

利用自平衡试桩试验拟合的模型参数代入前面所提出的荷载传递解析方程，从而得到类似于传统静载荷试验Q-s曲线。考虑到上段桩摩阻力为负摩阻力，对上段桩弹性阶段抗剪刚度k1及塑性软化阶段抗剪刚度系数k2根据自平衡法试验规范[7]进行修正。

式中：η为土层修正系数，黏土取0.8。将修正后的模型参数代入2.1中的荷载传递解析方程可得上段桩解析转换的Q-s曲线，其中上段桩极限承载力为

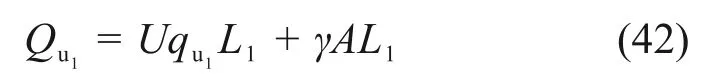
式中：qu1为上段桩极限侧摩阻力。

对下段桩而言，利用桩端计算参数k5，k6和se以及试验实测曲线拟合得到的k3，k4和sc，可根据下段桩荷载传递解析公式绘制Q-s曲线，其中下段桩极限承载力为

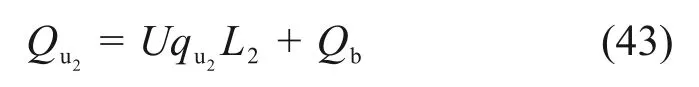
式中：qu2为下段桩侧极限摩阻力；Qb为下段桩端极限承载力，可根据图3中桩端土假定模型进行求解。最后利用等荷载法将上、下段桩Q-s曲线转换为传统单桩静载受压试验的Q-s曲线。

4 方法验证与分析

本文采用室内模型试验对自平衡试桩静载试验和传统静压静载试验过程进行模拟，试验时通过逐级加载至桩身破坏，得到单桩极限承载力[21]。并在桩身粘贴应变片获得桩身内力，通过与传统静载试验结果对比分析，验证针对黏土地基中自平衡试桩法的准确性，并得出相关结论。

4.1 试验方案

4.1.1 试验装置

采用自主研制的室内试桩加载装置对黏土地基中自平衡试桩及传统静压试桩承载特性进行试验。试验装置包括模型箱、模型桩、底座、支架、砝码和数据采集系统，具体布置如图4所示。

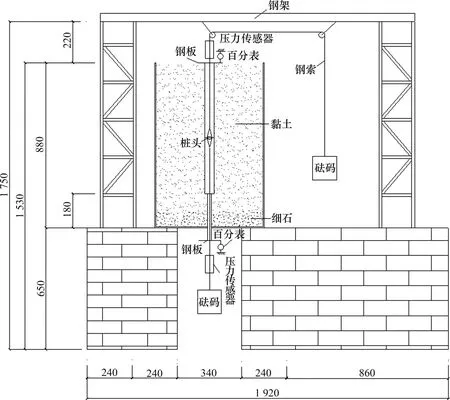
图4 试验装置正面图Fig.4 Front view of test device

1)模型箱：采用高为880 mm，直径为580 mm，壁厚为3 mm的钢桶作为本次试验的模型箱，模型箱底部加焊3 mm的圆形钢板，防止夯土导致底部变形。

2)加载装置：传统静压桩和自平衡试桩法分别通过定滑轮连接绳索悬挂码篮，初始加载为10 kg码篮质量，往后每级添加5 kg或10 kg砝码逐级加载。

3)数据采集装置：通过在桩端设置的LH-S02传感器精确测量试验中每加一级荷载，在LHPT600高速显示仪表面板显示每级荷载；采用量程为50 mm 的百分表测量桩体位移，用磁性表座固定在顶面和钢架上；采用TST3822EN 无线静态应变测试分析系统，对加载过程中桩身应变片数据进行监测。

4.1.2 模型桩制作

试验模型传统静载桩C1和自平衡试桩的上段桩Z1、下段桩Z2均采用外径为25 mm、壁厚为2 mm 的铝合金空心管制作。桩身入土深度为670 mm，土体以上长度为30 mm，桩顶下20 mm处一侧开设10 mm圆孔，用于引出应变片连接线。在桩体内部粘贴一定数量的应变片时，为防止加载过程中应变片受损，将应变片粘贴在桩体内壁，需要把铝合金空心管模型桩从中心对半精密剖开，在剖开的模型管桩内壁标记应变片位置，将应变片和接线端子粘贴标记处，并标记每根导线对应的应变片，每个应变片间距均匀设为50 mm，并对各应变片进行编号。试验采用浙江台州黄岩测试仪器厂生产的长×宽为4 mm×5 mm 接线端子和BX120-3AA 型应变片，如图5 所示。剖开的模型桩需要使用环氧树脂粘结成桩，同时模型桩两端采用铸铁桩头封住，另外，为模拟实体桩表面粗糙度，在模型桩表面涂抹一薄层环氧树脂，并洒上粒径为1 mm左右的砂粒。

图5 应变片布置图Fig.5 Layout of strain gauge

当竖向受荷桩的土体边界大于单桩半径的10倍时，可以忽略边界影响。本次试验模型桩与边界之间距离大于3倍直径，计算可知模型桩与边界间距离满足边界效应要求。试验中模型桩在模型箱中的平面布置图及剖面布置分别如图6 和图7所示。

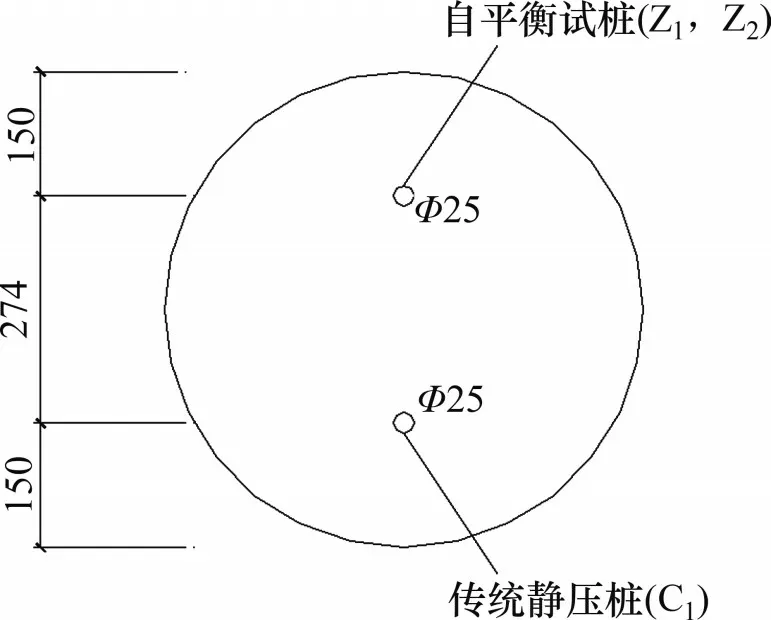
图6 模型桩布置平面图Fig.6 Layout plan of model pile

图7 模型桩布置剖面图Fig.7 Section of model pile layout

4.1.3 试验用土

试验用黏土土样取自广西南宁某工地现场，土体经过烘干、粉碎，制成含水率为25%的土样，其相关物理参数如表1所示，试验土样经过人工夯实按每100 mm分层填筑，夯每一层土时，通过测量桩身与重锤线之间距离，检验桩体垂直度，以满足试验要求。

表1 土样基本物理参数Table 1 Basic physical parameters of soil samples

4.2 试验内容

试验包括2组模型加载工况：第一组对传统静压试桩进行逐级加载，直至试桩破坏；第二组为自平衡试桩进行逐级加载，直至试桩破坏。

4.2.1 桩身模型参数测量

试验模型桩参数包括桩长、桩径、质量、弹性模量，测得各段桩参数见表2。

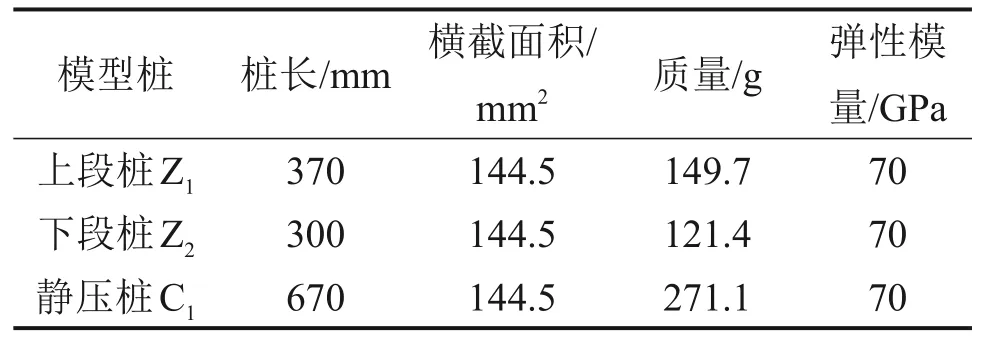
表2 桩体弹性模量测试结果Table 2 Test results of pile elastic modulus

4.2.2 试验加载方案

试验采用5 kg或10 kg的砝码逐级加载，每级加载为预估极限荷载的1/10。在加载过程中，采用慢速维持加载法，每级荷载持续1 h，加载后待压力传感器仪表盘上数据稳定后记录荷载，根据JGJ/T 403—2017“建筑基桩自平衡静载试验技术规程”[7]，当荷载或位移达到规定要求时终止加载。

4.3 试验结果及分析

4.3.1 试验结果

1) 试桩各级加载及位移。以向上位移为正，向下为负，传统静压桩、自平衡试桩2种工况下模型试验各级荷载-位移曲线如图8所示。

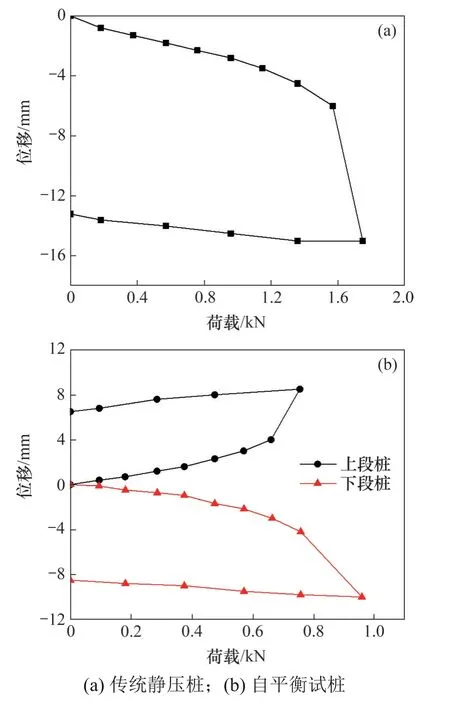
图8 试桩Q-s曲线图Fig.8 Q-s curves of pile testing

2)桩身轴力分布。

式中：Nij第i级荷载第j段桩身轴力；εij第i级荷载第j段桩身应变；E为桩身弹性模量；A为桩体截面面积。

桩身轴力分布如图9所示。荷载遵循从加载端向远离端传递的规律，自平衡上段桩从桩底进行加载，荷载自下而上传递，轴力离加载点位置越近轴力越大，并向桩顶逐渐衰减，随着荷载增加，所施加荷载由桩身下部土层承担逐渐转为上部土层发挥作用。自平衡试桩、静压试桩轴力基本随荷载呈线性增加，越靠近加载端线型斜率越大，反之，远离加载端斜率越小，轴力增量越小。从线形疏密程度来看，三者的轴力衰减规律不同，曲线越疏轴力衰减越大，则该部分土层承担的荷载较大，上段桩在加载点0～15 cm长度范围内曲线较疏，衰减量为46.67%～60.85%。静压试桩中部1/3 桩长曲线较疏，轴力曲线大致呈反“S”型，衰减量为41.26%～45.06%，桩身轴力从加载点至0.55 m土层范围承担的荷载较大。

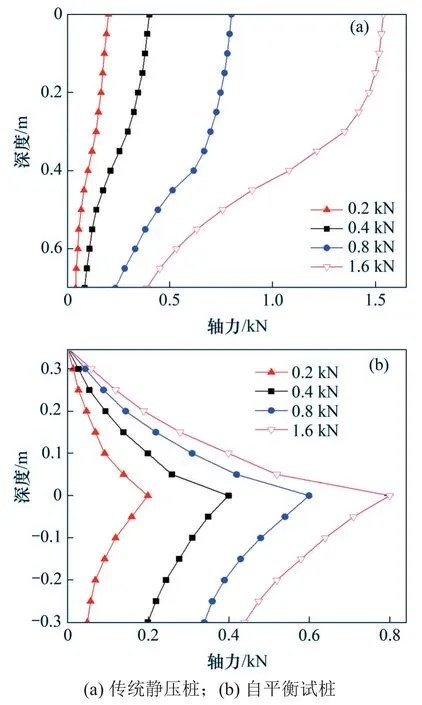
图9 各级荷载下试桩身轴力分布图Fig.9 Distribution of axial force of test pile body under different loads

3)桩身侧摩阻力分布。

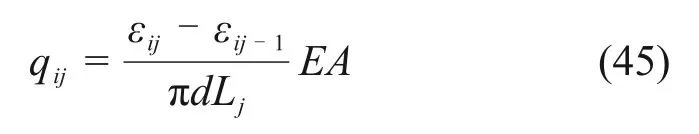
式中：qij为第i段荷载时第j段桩身侧摩阻力；d为桩直径；Lj为第j段桩身长度。得到第j段平均侧摩阻力，并把此值作为该段中点处的侧摩阻力，依次连接各中点得到平滑的曲线作为桩身侧摩阻力分布，如图10所示。

由图10 可知：自平衡上段桩侧摩阻力分布呈下大上小特征，随荷载增加，桩身各点侧摩阻力均增大，而侧摩阻力增量从桩身下部往上逐渐减小。自平衡试桩上段桩曲线类似双曲线形，上段桩侧摩阻力在桩端0.05 m 处出现峰值，随后出现软化的特征，在桩底附近桩侧摩阻力呈缓慢增长趋势，同时下段桩侧摩阻力弹塑性发展规律亦出现此特征。传统静压桩侧摩阻力发挥呈中间大，两端小的特征。在桩顶位置附近，侧摩阻力最先开始发挥，达到一定应力水平后，桩顶侧摩阻力接近极限值，并出现弱化，随着荷载增加，桩身中下部土层摩阻力逐渐发挥。

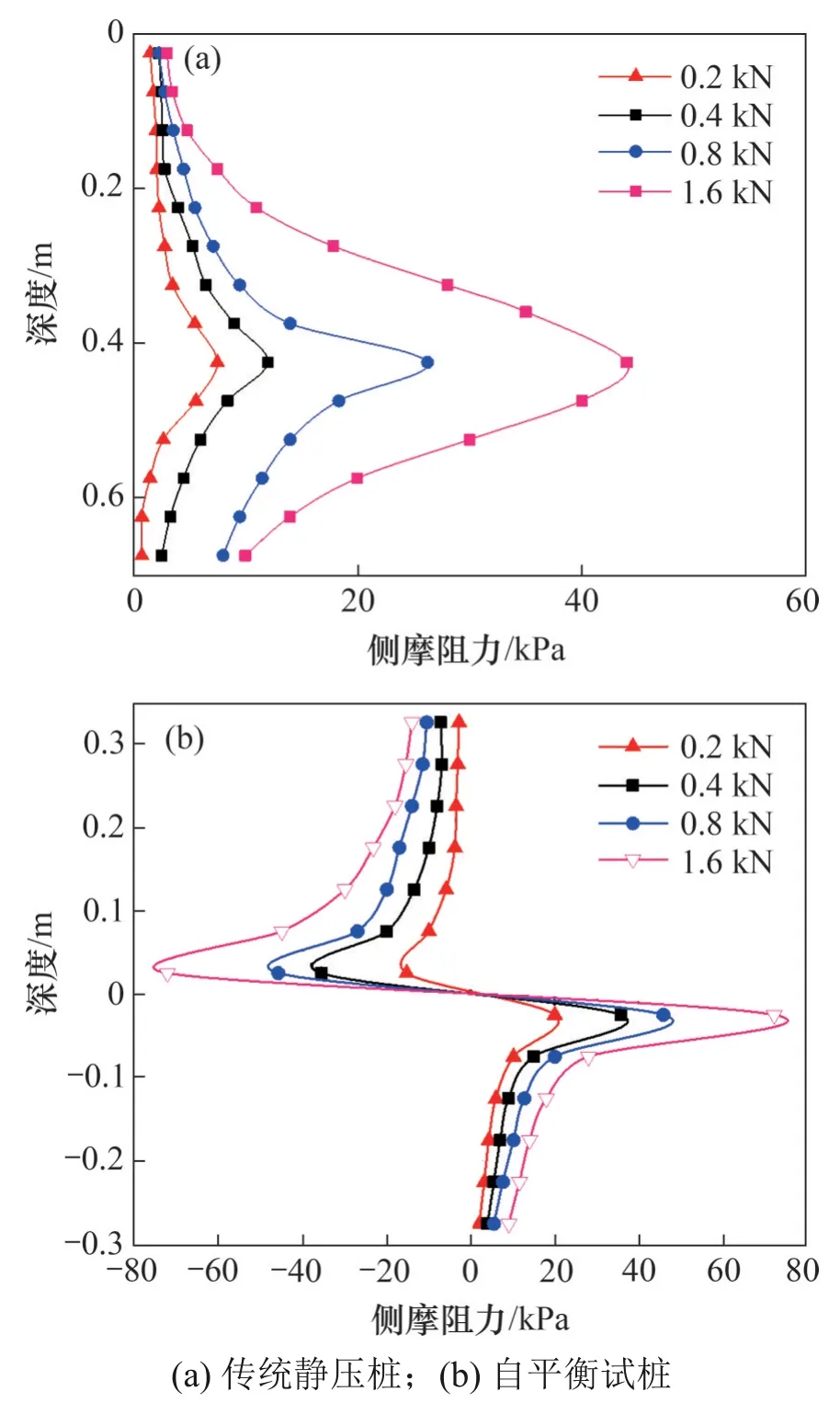
图10 各级荷载下试桩身侧摩阻力分布图Fig.10 Distribution of side friction resistance of test pile body under different loads

4.3.2 等效转换结果

利用上述试验数据，采用本文解析转换法拟合模型试验桩侧抗剪刚度系数及弹塑性位移计算参数：对上段桩，k1=1 993.465 kPa/m，k2=-106.265 kPa/m，sa=1.6 mm，sb=5.8 mm；对下段桩，k5=235.27 MPa/m，k6=0 MPa/m，se=3.5 mm，k3=1 345.096 kPa/m，k4=-54.792 kPa/m，sc=1.5 mm。将以上模型参数代入理论解析公式中，得到解析转换法Q-s曲线，与传统静压桩实验结果以及自平衡试桩精确转换法、简化转换法所得结果对比如图11 所示。在加载过程中，对于传统静压桩，桩顶累积位移为13.2 mm，加载前期位移随荷载增加呈缓慢增加，当荷载增加到1 360 N时，位移增量有增大趋势，继续增大1 750 N 时位移达15.0 mm，卸载后回弹量仅为1.8 mm，已超出弹性工作范围，可判定试桩已发生破坏，取1 560 N为静载试桩极限承载力。对本文中自平衡试桩解析转换法，上段桩顶与桩底Q-s曲线发展趋势基本相同，在转换Q-s曲线中，当桩位移达到塑性软化阶段sa=1.6 mm 时，加载位移随荷载增加幅度逐步加快增加，当位移达到理想塑性阶段sb=5.8 mm 时，加载位移随荷载明显增大。可判定试桩周围土体已达到理性塑性阶段，对应求得试桩极限承载力为1 575 N。同时，采用精确转换法求得极限承载力为1 592 N，而使用简化转换时，分别取上、下段桩拐点处对应荷载为极限荷载，上、下段桩极限承载力分别为720 N和832 N，以γ=0.82的转换系数可得承载力为1 710 N。

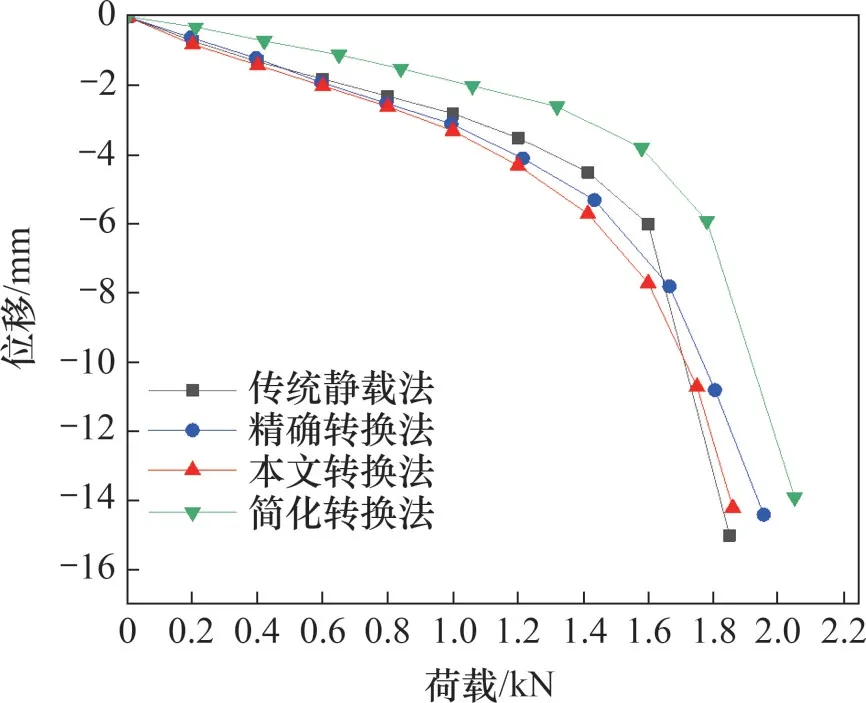
图11 自平衡等效转换与传统静压Q-s曲线Fig.11 Equivalent conversion of self-balance and conventional static pressure Q-s curve

综上分析，相比于简化转换法，本文提出的针对黏土地基自平衡试验解析转换法的Q-s曲线效果更好。对单桩承载力而言，本文方法所求解的试桩极限承载力更接近于传统静压试验和精确转换法所得承载力，而简化转换结果偏大，在本次模型试桩试验中，本文转换方法比简化转换结果精度提高约9.6%。

5 结论

1)通过室内模型试验对本文解析转换方法进行验证，并与传统静压试验以及简化转换法对比发现，本文解析转换法与传统静压试验的Q-s曲线结果吻合效果较好，与精确转换法结果较接近，可见本文方法有一定的可行性，同时相比简化转换法所得承载力，其精度有很大提高，证实了本文解析转换法的准确性。

2)本文转换方法具有完整的理论基础，且能较好地反映自平衡试桩上、下段桩的承载特性以及桩侧摩阻力和桩身轴力分布规律，具有一定的实用性。且本文自主研发的自平衡室内模型加载试验具有明确的目的性和针对性、避免了加载点位置、周围边界条件等不确定因素产生的试验误差，为今后研究非均质及特殊土层等情况下桩基承载力模型试验研究提供试验基础。

3)本文对均质土层中自平衡试桩荷载传递理论解析进行了分析，该方法亦适用多层地基及特殊土层中，可考虑成土层的连续条件及特殊土的性质进行求解，同时设置多组对比试验来分析验证自平衡试桩单桩承载特性，这是下一步需要深入研究的内容。