深覆土明洞及其减载结构渐进性破坏机理模型试验研究

卓彬，王飞阳，方勇，周凯歌，朱牧原，李盛

(1.西南交通大学交通隧道工程教育部重点实验室，四川成都，610031；2.兰州交通大学道桥工程灾害防治技术国家地方联合工程实验室，甘肃兰州，730070)

我国西部山区城市周边或内部常出现沟谷地形，沟谷走向各异，宽度大小不一。为了适应该类城市复杂的地质条件，满足土地的连续性，采用隧道—明洞—隧道形式通过沟谷的方案开始得到应用，导致了深覆土明洞这类特殊结构的诞生。与普通明洞相比，覆土深度可达30～50 m，是一般明洞覆土深度的5倍以上[1-2]，如此大的埋深势必导致结构所受荷载较大，衬砌易出现裂缝，导致结构失稳破坏，难以正常使用。近年来，在深覆土明洞结构力学特性方面的研究主要有：李盛等[3-4]通过数值模拟研究了高填方明洞截面内力随覆土深度的变化规律，基于柔性减载材料的力学性质，提出了最佳减载措施。王玉锁等[5-6]以拱形铁路明洞工程为依托，综合采用动力有限元、离散元和相似模型试验的方法，研究了不同落石冲击角度、高度、质量和速度作用下的明洞结构力学特性。徐湉源等[7-8]采用有限元模拟和现场实测的手段，研究了双层衬砌深埋明洞的受力特性，为深埋明洞结构设计提供了参考。然而，以上分析仅考虑了弹性阶段的明洞结构内力，未考虑深覆土明洞衬砌结构出现裂缝后的结构位移及内力变化规律。

国内外学者关于隧道衬砌结构力学性能及开裂破坏进行了相关研究。CHEN 等[9-10]通过建立数值模型，研究了盾构隧道中的裂缝对其在施工及使用过程中受力特性的影响。何川等[11]以实际盾构隧道工程为依托，通过相似模型试验，研究了不同裂缝数量、宽度、深度和位置等对盾构隧道结构力学特性的影响，发现裂缝将降低衬砌整体刚度，同时结构承载力也随之降低。GUTTLER 等[12]采用橡皮膏与高岭土混合料模仿喷锚支护，通过离心模型试验对隧道衬砌结构变形及破坏进行了深入研究。FUMAGALLI[13]采用模型试验，对隧道围岩进行了破坏性加载，研究了隧道围岩弹塑性变形关系，发现围岩具有非均匀性及非线弹性等特点。KASHIMA等[14]通过原型试验，分析了矩形断面盾构管片的变形及力学特性，揭示了不同加载参数下衬砌变形与受力情况。邱月等[15-16]通过室内相似模型试验及数值模拟，采用声发射技术对盾构管片的渐近性破坏机理进行了深入研究，发现第一条裂缝的产生与结构刚度相关，刚度越大，裂缝越容易出现。以上研究成果主要是对隧道衬砌力学性能和裂损破坏过程进行了研究。然而，深覆土明洞与现有隧道相比，虽然断面尺寸相似，但在修筑方式、荷载作用等方面存在明显差异。

鉴于此，本文作者以深覆土铁路明洞工程为依托，采用室内模型试验分析明洞衬砌结构声发射数据、位移、内力和裂缝随覆土深度的变化规律。随后，在明洞顶铺设与明洞等宽的EPS 板，针对明洞在深覆土作用下的开裂问题展开研究，此研究可为明洞衬砌在深覆土作用下的结构安全评估提供参考。

1 工程背景

某铁路工程范围内沟壑纵横，地势高低不平，区内大部分为荒地，人为开挖及回填现象严重，对工程周边地形影响较大。对于新建的明洞工程，需要通过回填来保证线路运行条件良好。该明洞设计覆土最大深度30 m(拱顶至覆土表面)，如此大的埋深容易导致明洞受力较大，结构易出现裂缝，造成结构破坏，难以正常使用，故施工人员拟采用铺设EPS板的措施对结构进行减载。图1 所示为深覆土减载明洞衬砌工程示意图。填土采用分层填筑，共填土6 层，每层5 m，明洞宽×高为12.8 m×11.8 m，明洞两侧采用边坡支撑，是典型的沟槽式深覆土明洞工程，边坡坡角为70°，槽宽比为1。为控制高速铁路地基沉降，确保高铁安全运行，采用C30混凝土修筑明洞基础。

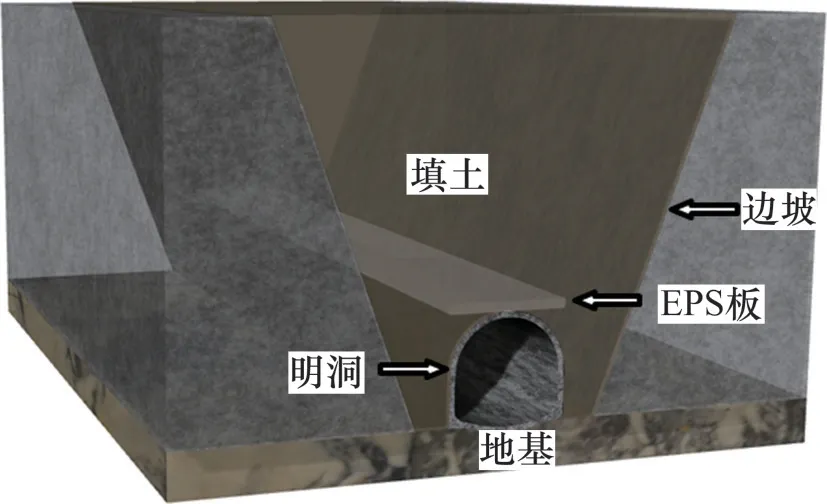
图1 深覆土减载明洞衬砌工程示意图Fig.1 Schematic diagram of high-filled cut-and-cover tunnel

2 室内模型试验

2.1 相似关系

模型试验作为解决岩土工程问题的一种重要途径，具有直观性、经济性及可控性等优势，能够反映结构的实际受力状态。本次试验以铁路明洞衬砌结构为对象，研究深覆土荷载、超载及EPS板减载作用下的力学行为和破坏特征。采用常重力条件下的地质力学模型试验，根据相似第二定理(具体理论及表达式参考文献[17-18])。原型覆土深度为30 m，模型试验总覆土深度为1.5 m，由此可确定几何相似比CL=20 和重度相似比Cγ=1，并将其作为基础相似比，由相似理论可推导其余物理量相似比：泊松比、应变、摩擦角的相似比Cμ=Cε=Cφ=1，强度、应力、黏聚力和弹性模量的相似比CR=Cσ=CC=CE=20，轴力相似比CN=CσCL2=8 000，弯矩的相似比CM=CσCL3=160 000。

2.2 材料参数及相似模型

2.2.1 实际材料参数

根据实际情况中的边坡与土体之间的摩擦，对模型试验中的边坡进行凿毛处理，使其摩擦因数与实际相符。边坡的弹性模量为4.2×103MPa，泊松比为0.30，重度为22.0 kN/m3；明洞地基的弹性模量为55.0 MPa，泊松比为0.25，黏聚力为76.0 kPa，内摩擦角为33.0°，重度为20.0 kN/m3。试验覆土与实际工程中的覆土具有相同力学性质，其最优含水率为16.15%，最大干密度为1.59 g/cm3。为了控制试验覆土的压实度，采用人工夯实的方式对其预压，确定覆土压实度K为85%。具体材料参数如表1所示。

表1 实际材料参数Table 1 Material parameters of model test

2.2.2 模型衬砌材料参数

实体工程中边坡与地基由混凝土材料浇筑而成，实际工程中的边坡和地基在回填土作用下几乎不发生变形。因此，本模型试验不考虑边坡和地基的影响，采用刚性较大的预制混凝土模板和C50混凝土分别模拟边坡和地基。模型衬砌采用石膏、硅藻土等材料制备，具有混凝土材料的物理力学性能，因此，明洞模型衬砌采用石膏硅藻土模拟。通过不断调整各组分配比，最终确定明洞衬砌相似材料质量配合比为m(水)∶m(石膏)∶m(硅藻土)=1∶1.30∶0.1。模型与原型衬砌物理力学参数如表2所示。

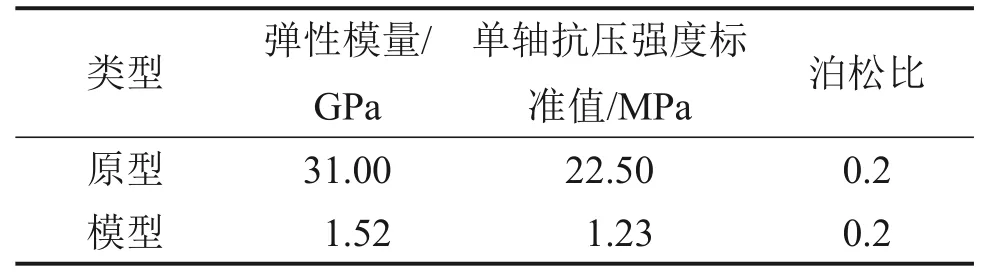
表2 模型与原型衬砌物理力学参数对照Table 2 Comparison of physical and mechanical parameters of cut-and-cover tunnel model with prototype material

明洞模型衬砌主筋采用直径为1.3 mm 的钢筋网，通过原型与模型等效抗弯刚度EI相似的方法模拟[15-16](其中，E为衬砌的弹性模量，I为衬砌截面惯性矩)，从表2 可见模型衬砌材料与原型混凝土衬砌材料的弹性模量相似，因此，只需保证衬砌截面惯性矩相似。对于矩形截面，其惯性矩计算公式为I=ba3/12(其中，b为截面宽度，a为截面厚度)。由于本模型试验考虑的是平面应变问题，可取截面宽度b为单位1，因此，通过相似原理和截面惯性矩计算公式可确保模型与原型的抗弯刚度EI等效相似。

2.2.3 EPS板材料参数

EPS 板密度的不合理取值势必影响其减载效果，其密度的选取主要由明洞覆土深度及沟槽坡角决定。本文参考已有研究成果，由文献[3]可知，50 m覆土深度、70°坡角的沟槽式明洞宜选用密度为12 kg/m3的EPS板。本文所依托工程实际覆土深度最大为30 m、边坡角度为70°，为了研究超载下结构受力及破坏过程，试验模拟最大覆土深度达50 m，故减载材料选用密度为12 kg/m3的EPS板。

2.3 试验设计及测试

为了模拟现场深覆土分层回填过程，在模拟箱内进行明洞回填模型试验。利用自制模型箱(长为360 cm，宽为120 cm，高为209 cm)，按照相似比例1∶20制作明洞模型，沟槽坡角为70°，槽宽比为1，模型断面如图2(a)所示，明洞减载试验模型如图2(b)所示。

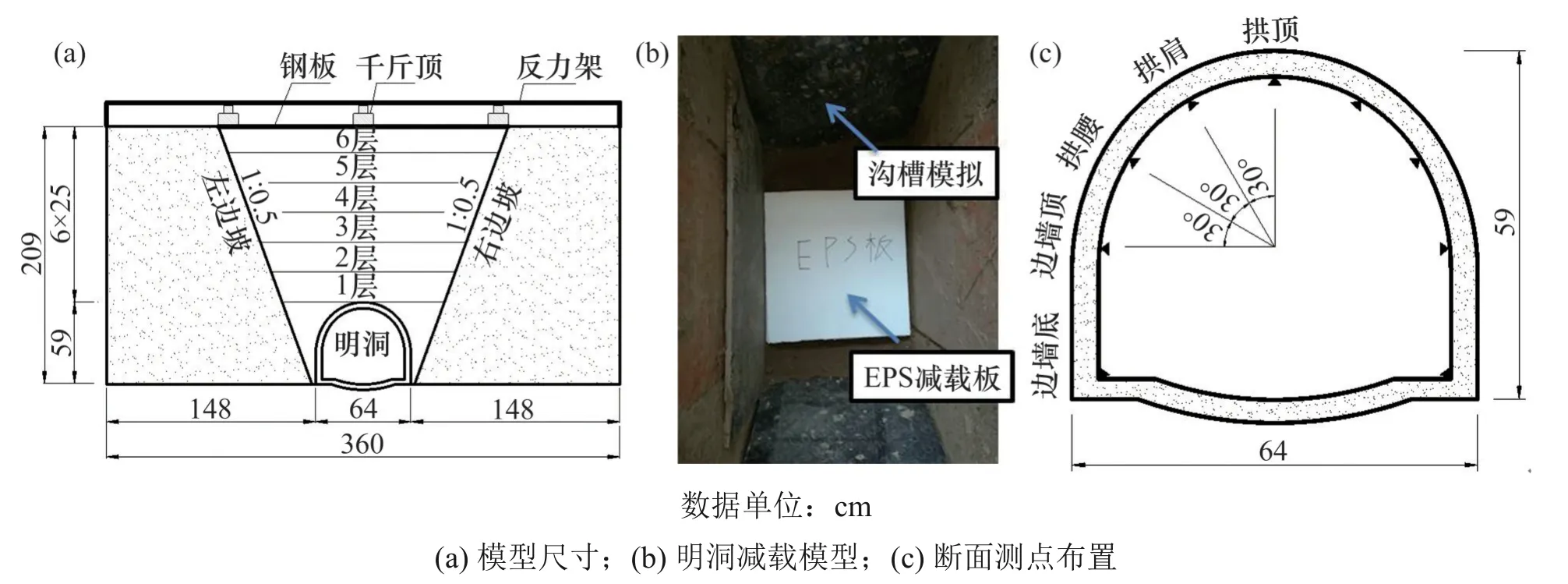
图2 深覆土明洞相似模型试验Fig.2 Model test of high-filled cut-and-cover tunnel

在模型试验及数值模拟分析过程中，定义系数λ为覆土深度与明洞结构高度的比值，即λ=H/h(H为覆土深度，h为明洞高度)，以此来反映原型明洞内力、位移及开裂信息随覆土深度的变化规律。现场明洞工程以5 m 覆土深度为一层，共计30 m，原型明洞结构高度为11.8 m。在试验填土过程中，根据相似理论计算每层覆土深度，以25 cm厚覆土深度为一层，共计6层，模型明洞结构高度为59 cm。因此，λ取值分别为0.42，0.85，1.27，1.69，2.12和2.54。

当覆土达到设计深度150 cm时(本文的覆土深度均是指由明洞拱顶至覆土表面距离)，此时，对应的实际工程中的填土高度为30 m，系数λ为2.54。为了模拟后期明洞在超载作用下的结构渐进性破坏的过程，利用千斤顶加压模拟后期的填土过程。在试验过程中，分级施加用于保证平面应变的竖直方向荷载。表3所示为试验加载工况，通过在拱顶背后埋设应变式土压力盒获得拱顶处土压力，根据实测土压力与上覆土荷载理论值得到明洞等效竖向土柱高度。为了体现超载及结构劣化等因素对明洞衬砌的影响，持续加载直至结构达到破坏失稳。为了体现EPS 板的减载效果，明洞两侧填土完成后，铺设厚度为2 cm 的EPS 板，采用相同的试验加载方案。

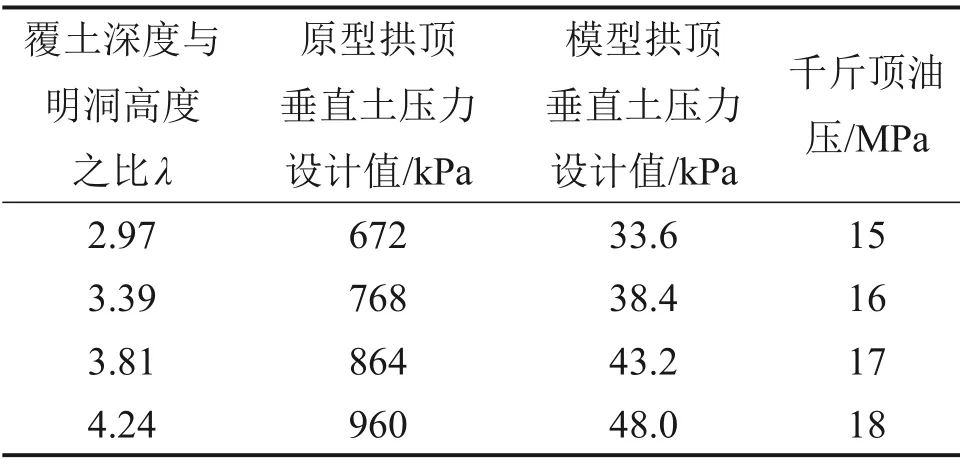
表3 试验加载参数Table 3 Loading parameters of model test

试验测量内容包括结构环向应变、结构位移、累计声发射事件数，并考察明洞在超载及减载条件下的结构受力特性和破坏形态，具体测点布置如图2(c)所示。其中，拱顶、拱肩、拱腰、边墙顶部、边墙底部的内外侧表面各粘贴1 个环向应变片，共计18 个，同时内侧安装5 个位移传感器。在拱顶、拱底、左右边墙处分别布置1 个声发射探头。

3 试验结果及分析

本文通过对深覆土明洞及其减载结构模型试验结果的分析，根据累计声发射事件曲线并结合位移和内力随λ的曲线斜率变化，将明洞衬砌累计声发射事件数、位移及内力随系数λ(覆土深度与明洞高度的比值)的变化过程大致分为3个阶段(平稳增长阶段、快速增长阶段、加速增长阶段)，用于描述深覆土明洞结构渐进性破坏发展过程同时验证EPS 板的减载效果，分析累计声发射事件数、位移、内力的变化规律。

3.1 声发射信息分析

声发射作为无损检测的常用有效手段，它能够准确获取明洞局部结构因损伤破坏而产生的瞬态弹性波，是反映结构失效的重要途径。明洞衬砌结构内部的破损程度可由累计声发射事件数反映，位移可反映结构在外荷载作用下的动态特征，根据累计声发射事件数变化曲线和位移随λ的变化规律，综合分析明洞衬砌结构渐进性破坏机制。

未铺设EPS 板的明洞衬砌在加载过程中累计声发射事件数随加载步变化的曲线如图3所示。

从图3可以看出：加载过程的累计声发射事件数存在明显的阶段性。累计声发射事件数在明洞衬砌结构损伤断裂过程的不同阶段表现出不同特性，结合不同阶段的变化规律，对明洞的损伤断裂机制进行分析。在每个加载段，累计声发射事件数增长梯度越大，说明声发射信号活度越大，明洞结构损伤发展速率越快；在每个加载阶段，累计声发射事件数越大，说明损伤发展程度越大。

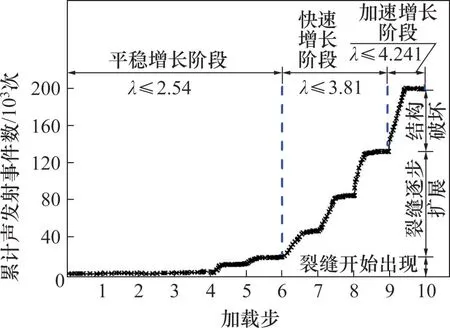
图3 明洞衬砌累计声发射事件数变化曲线Fig.3 Variation curve of cumulative number of acoustic emission events of cut-and-cover tunnel

平稳增长阶段、快速增长阶段、加速增长阶段分别对应明洞衬砌结构裂缝发展的3个过程，图3 中3 个阶段的划分依据主要结合明洞衬砌结构位移、内力和裂缝随系数λ的发展过程，明洞结构位移和内力在数值上均出现突增现象，而裂缝由开始出现到逐渐扩展再到裂缝发展到一定程度致使结构失稳破坏整个过程。由图3 可知：当λ≤2.54时，无损明洞衬砌从开始加载至第6级荷载，平稳增长阶段累计声发射事件数较少，说明该阶段明洞衬砌结构以弹性变形为主，结构局部开始产生细微裂缝，表明结构在外载作用下已产生轻微局部损伤；当λ≤3.81时，第6级荷载加载至第9级荷载，快速增长阶段结构以塑性变形为主，累计声发射事件数呈台阶状增长且台阶梯度逐渐增大，曲线斜率相对平缓，裂缝增长速率为稳定值。表明结构在外载作用下已产生局部损伤且损伤区域逐渐扩展；当λ≤4.24，即最后一次加载时，加速增长阶段累计声发射事件数曲线斜率突然明显增大，台阶数量明显减少，表明结构在第10 级荷载作用下因外荷载过大而失稳破坏。

为了证明EPS 板减载的有效性，采用相同的试验加载方案。减载明洞衬砌在加载过程中声发射事件数随加载步变化的曲线如图4所示。

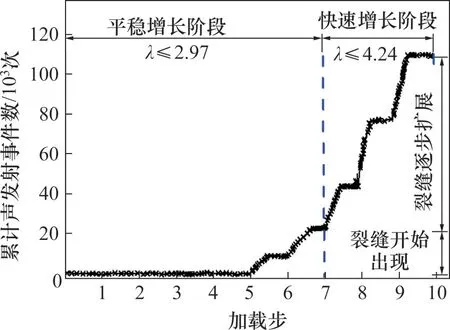
图4 减载明洞衬砌累计声发射事件数变化曲线Fig.4 Variation curve of accumulative number of acoustic emission events of lining of load reduction cut-andcover tunnel

对比分析未减载明洞衬砌结构失稳临界点的声发射信息，明洞上方铺设EPS 板后，减载明洞的累计声发射事件数在λ为2.54，3.81 和4.24 时分别减少了109.27%，55.18%和82.24%。

由图4可知：平稳增长阶段、快速增长阶段分别对应减载明洞衬砌结构裂缝发展的2个过程，即裂缝开始出现和裂缝逐渐扩展；当λ≤2.97 时，减载明洞衬砌结构以弹性变形为主，结构裂缝开始出现；当λ≤4.24，即最后一次加载时，减载明洞衬砌结构以塑性变形为主，结构裂缝逐渐扩展。加载完成后，结构并未破坏，其主要原因是明洞两侧填土完成后，在明洞拱顶铺设EPS 板，明洞上方内侧土柱直接作用于EPS板，EPS板产生压缩变形，内侧土柱与两侧土柱产生错动位移，从而形成土拱效应，部分外荷载由土拱传递至两侧边坡，进而改善结构受力[1-4]。由此可知，铺设EPS 板有助于缓减裂缝发展，避免结构因荷载过大而破坏。

3.2 衬砌结构位移

根据几何相似比20 换算后得到的原型明洞衬砌位移随系数λ的变化规律。明洞位移以向明洞内侧变形为“+”，外侧变形为“-”。

由图5可知：当系数λ处于AB段时，明洞衬砌结构位移随着系数λ增长虽有少量增加但变化不明显，结构处于平稳增长阶段；随着系数λ不断增加，BC段明洞衬砌各截面位移均呈小幅度增加趋势，其中，拱顶、拱肩向内侧变形逐步增加，拱腰、边墙截面向外侧变形逐步增加；C点之后，各关键点位移增速迅速增大，向明洞内、外侧变形最大位置分别位于拱顶、边墙底部截面，拱顶变形已达明洞高度的2.7%。

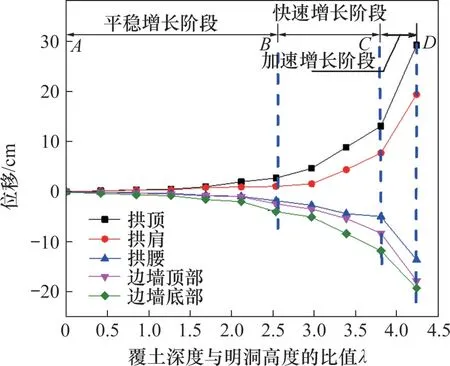
图5 明洞衬砌结构位移随系数λ的变化规律Fig.5 Variation law of displacement of cut-and-cover tunnel with coefficient λ

结合明洞衬砌结构裂缝分布图分析可知，当λ=1.27(即覆土深度为明洞高度的1.27 倍)时，结构各截面位移仍然处于平稳增长，曲线变化平缓，这是由于拱顶出现的第一条细微裂缝对结构各截面位移几乎没有造成影响；当λ=2.54 时，结构各截面位移开始进入快速增长阶段，拱顶裂缝和边墙出现的多处细微裂缝对结构位移开始造成影响；当λ在2.54～3.81 之间时，该阶段裂缝发展加快，同时结构各截面位移快速增加；当λ=4.24 时，结构各截面位移均达到最大值，结构体系发生转变，明洞整体结构失稳破坏。

图6所示为减载明洞拱顶、拱肩、拱腰、边墙顶部、边墙底部及仰拱衬砌结构位移随系数λ的变化曲线，图7 所示为减载前后明洞结构各部位(拱顶、拱肩、拱腰、边墙顶部和边墙底部)的位移对比。

图6 减载明洞衬砌结构位移随系数λ的变化规律Fig.6 Variation law of displacement of load reduction cutand-cover tunnel with coefficient λ

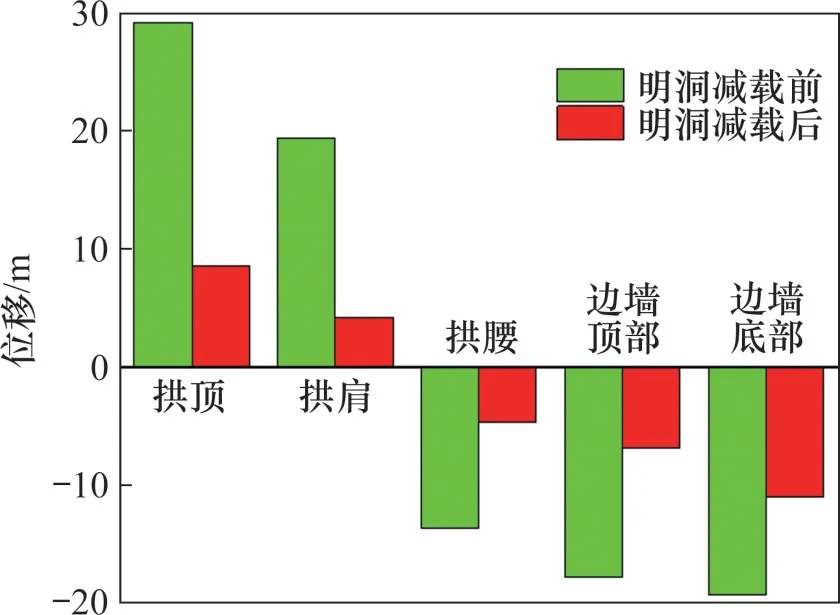
图7 当λ为4.24时减载前后明洞各部位位移结果对比Fig.7 Comparison of displacement results of each point of cut-and-cover tunnel with load-reduction cut-and-cover tunnel as λ is 4.24

由图6可知：减载明洞衬砌结构位移随着系数λ的变化规律与未减载明洞结构位移发展初期(AB段和BC段)规律相似，当λ=2.97时，减载明洞各截面位移开始进入快速增长阶段，拱顶裂缝和边墙出现的多处细微裂缝对结构位移开始造成影响，位移和裂缝发展均处于快速增长阶段。直至加载完成后，位移和裂缝均未达到加速增长阶段。从图7 可知：当系数λ为4.24 时，减载后明洞拱顶、拱肩、拱腰、边墙顶部和边墙底部位移分别减少20.66，15.22，8.93，11.00和8.27 cm，表明明洞顶铺设EPS 板有助于延缓结构位移和裂缝发展，避免结构因外荷载过大而提前破坏，使结构具有更好的延性。

3.3 衬砌结构内力

混凝土衬砌在荷载超过一定范围后，表现出明显的非线性力学行为，这种非线性行为主要由损伤演化(微裂隙的发展、融合及贯通等)控制[19]。通过测试明洞衬砌结构(拱顶、拱肩、拱腰、边墙顶部、边墙底部)内外侧应变，由材料力学理论和混凝土的本构关系换算成原型明洞衬砌结构内力(弯矩和轴力)，如图8 所示，其中，弯矩以下部受拉为“+”，轴力以拉为“+”，轴力以压为“-”。

图8 明洞衬砌结构内力随系数λ的变化规律Fig.8 Variation law of internal force of cut-and-cover tunnel with coefficient λ

由图8可知：第一阶段为平稳增长阶段，明洞衬砌结构关键截面内力(轴力和弯矩)大致呈线性增加且变化缓慢，弯矩和轴力变化最大速率分别为20.59 kN·m/m 和50.08 kN/m，此阶段结构整体没有发生损伤破坏。第二阶段为快速增长阶段，此阶段明洞内力增长速率较第一阶段有一定增加，弯矩和轴力变化最大速率分别为44.00 kN·m/m 和80.95 kN/m，此时，明洞结构呈局部压溃状态。第三阶段明洞弯矩和轴力增长有明显突变，这可能是明洞大部分关键位置已破坏失稳造成的。

结合明洞衬砌结构裂缝分布图可知，当λ=1.27时，拱顶、拱肩、拱腰、边墙顶部和边墙底部弯矩与轴力的比值分别为0.58，0.02，0.15，0.23 和0.29，可见拱顶受弯矩控制作用最大，明洞拱顶内侧达到抗拉强度，使得明洞内侧出现第一条纵向地微裂缝，出现的原因是结构内侧受到较大弯矩导致张拉开裂；当λ=2.54 时，明洞边墙顶部和底部的弯矩和轴力相近，明洞拱顶、拱肩、拱腰、边墙顶部和边墙底部的弯矩与轴力比值分别为0.68，0.05，0.23，0.28 和0.30，由此可知，明洞拱顶受弯矩影响最大，其次为边墙顶部和边墙底部，因此，明洞衬砌结构拱顶裂缝进一步扩大，随后，边墙多处开始出现细微地裂缝；当λ=3.81和λ=4.24 时，明洞各截面弯矩与轴力的比值进一步变大。受弯矩影响，明洞衬砌各截面裂缝进一步扩大，甚至某些部位出现局部压溃现象，造成明洞衬砌表面应变突然变大，进而由应变反算的衬砌结构内力也突然变大，此时，明洞衬砌结构内力达到最终破坏前的峰值内力。综上所述，明洞结构的裂缝发展与结构内力相关，且受弯矩影响最大。

在明洞顶铺设与明洞等宽、密度为12 kg/m3、厚度为2 cm 的EPS 板，对明洞衬砌结构各位置处内力减载量及裂缝扩展过程进行研究，分析结构安全状态。试验结果如图9所示。

由图9可知：明洞衬砌结构内力减载量随系数λ增加而增加，弯矩减载量位置由大到小依次为拱顶、拱肩、边墙上部、拱腰、边墙底部。轴力减载量位置由大到小依次为拱腰、边墙顶部、边墙底部、拱肩、拱顶。

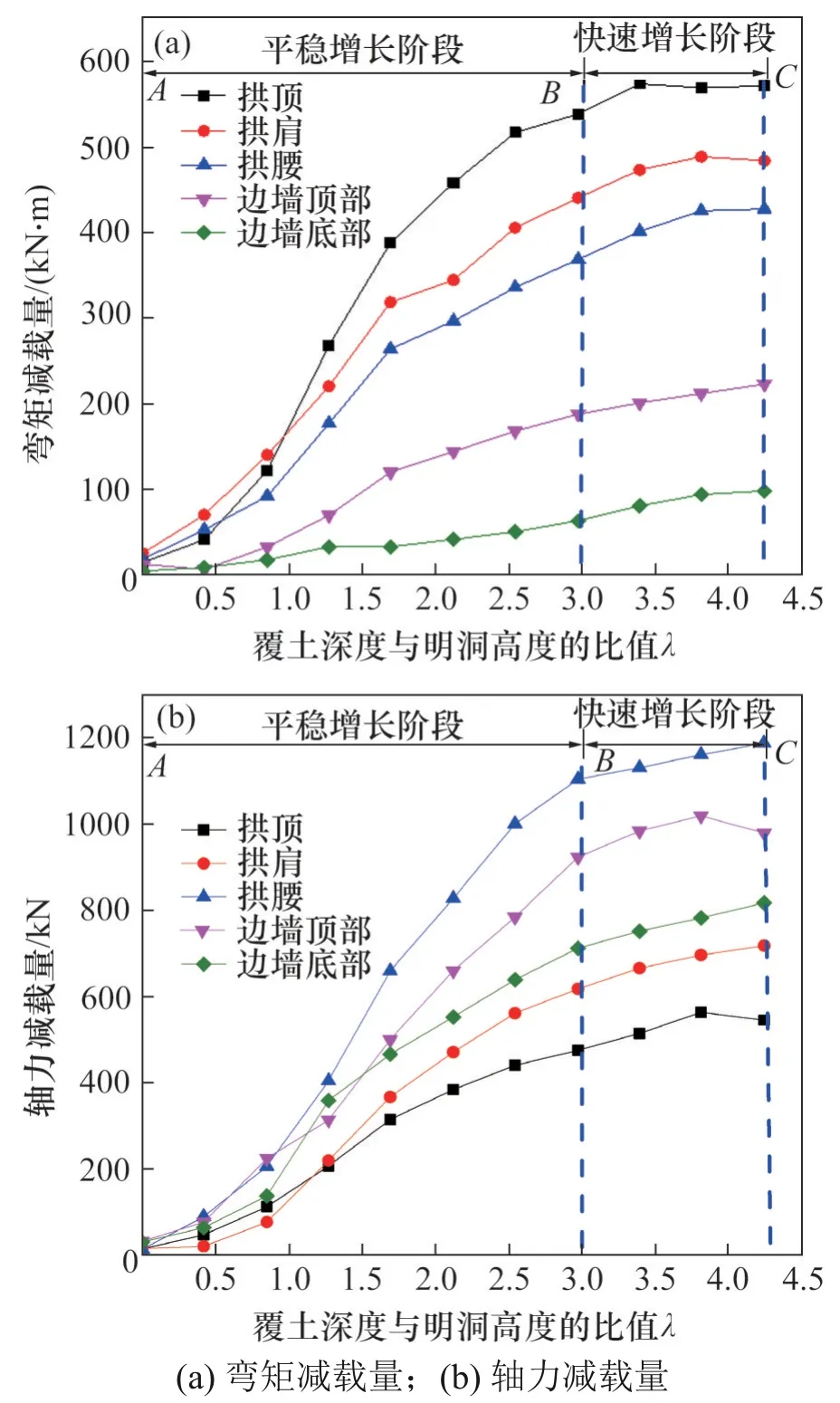
图9 明洞衬砌结构内力减载量随系数λ变化规律Fig.9 Variation law of internal force load reduction of cutand-cover tunnel with coefficient λ

衬砌结构各位置内力减载量斜率呈先增大后减小的趋势，这与EPS 板材料的应力应变关系曲线相关[2-3]。当λ≤2.97(AB段)时，减载明洞各截面内力减载量增长较快，减载效果明显；当2.97≤λ≤4.24(BC段)时,减载明洞各截面内力减载量增长缓慢，减载明洞拱顶和边墙出现多处细微裂缝，说明该阶段EPS 板对减小结构内力和抑制裂缝发展的作用开始削弱。

3.4 结构破坏过程

从宏观角度看，明洞衬砌结构破坏是裂缝逐步发展的过程。由上述分析可知，在相同试验加载方式下，减载明洞裂缝并未发展至破坏。本节以未减载明洞为例，对明洞在超载作用下的裂缝发展过程进行分析。图10和图11所示分别为不同系数λ(覆土深度与明洞高度的比值分别为1.27，2.54，3.81和4.24)时明洞衬砌结构裂缝分布图和明洞衬砌的裂缝分布素描图。

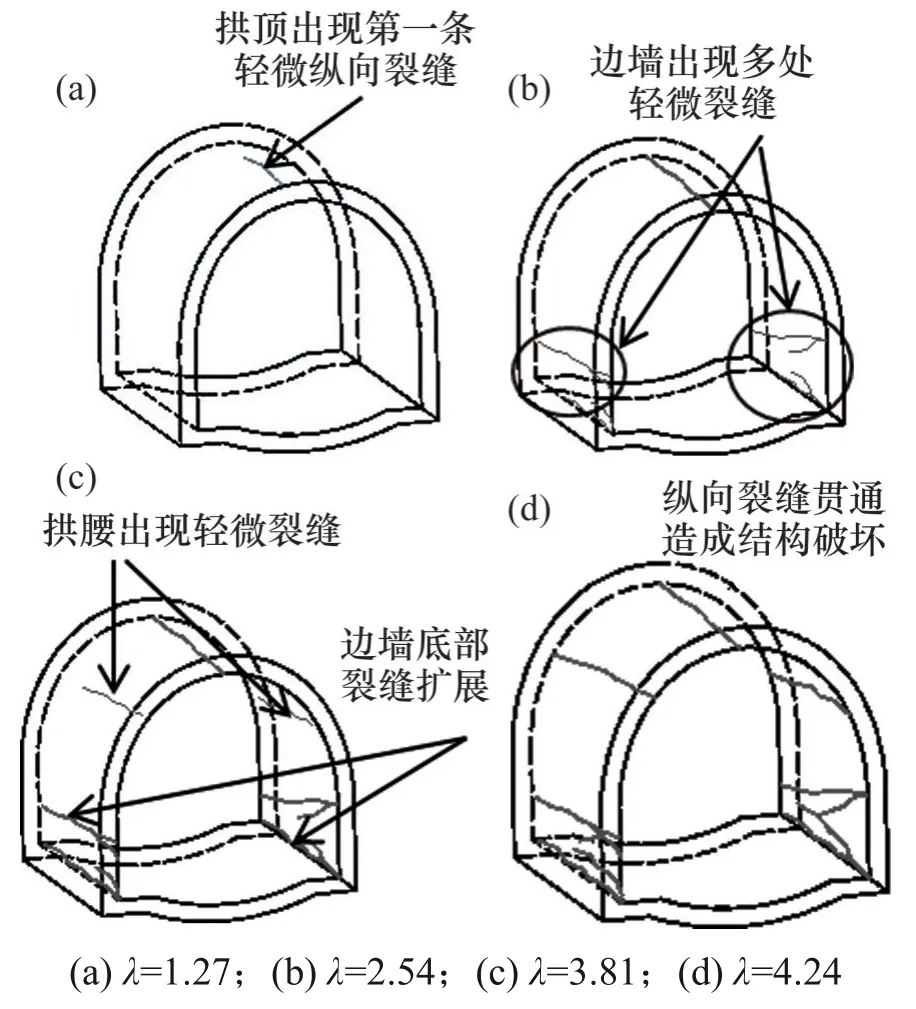
图11 明洞衬砌结构裂缝分布素描图Fig.11 Sketch maps of distribution of cracks in cut-andcover tunnel

由图10 和图11 可见：当覆土深度较低时，明洞衬砌结构所受荷载及变形较小，明洞外观无裂缝出现；随着覆土深度不断增加，当λ=1.27(即覆土深度为明洞高度的1.27 倍)时，明洞首先在拱顶内侧出现1条细微地纵向裂缝，裂缝宽度为0.04 mm，明洞衬砌结构局部呈轻微损伤状态，结构处于平稳增长阶段；当λ=2.54 时，明洞衬砌结构边墙多处出现细微裂缝，此时，拱顶内侧裂缝呈现为贯通性细微裂缝，裂缝宽度增长至0.12 mm，结构开始进入快速增长阶段；当λ=3.81 时，拱顶贯通裂缝宽度已达0.20 mm，此外，裂缝迅速蔓延，拱腰处裂缝逐步显现，边墙顶部出现局部小面积压溃现象；当λ=4.24(实际覆土深度50 m)时，拱顶、拱腰和边墙截面裂缝均为纵向贯通性纵向裂缝，拱顶裂缝宽度达0.43 mm，边墙顶部的局部压溃区进一步扩大，同时，拱顶内侧也出现局部压溃现象，结构整体破坏失稳。

4 结论

1)明洞衬砌结构声发射事件数、位移、内力及裂缝随着系数λ的变化过程大致分为3 个阶段：平稳增长阶段、快速增长阶段、加速增长阶段。在平稳增长阶段，明洞衬砌结构声发射事件数、位移和内力随着覆土深度增长虽有少量增加但变化不明显。随着覆土深度增加，快速增长阶段、加速增长阶段的声发射事件数、位移和内力增速较平稳增长阶段均有明显增加，这可能与明洞衬砌结构宏观裂缝逐步发展的过程有关。

2)当覆土深度较低时(小于2.54 倍明洞高度)，衬砌结构处于平稳增长阶段，明洞首先在拱顶位置出现轻微纵向裂缝，结构呈局部损伤状态。当覆土深度为2.54～3.81 倍明洞高度时，结构进入快速增长阶段，明洞衬砌结构拱顶、边墙多处出现宏观裂缝，此时拱顶裂缝呈现为贯通性裂缝，结构仍处于安全使用状态。当覆土深度大于3.81 倍明洞高度时，结构进入破坏失稳阶段，衬砌裂缝迅速蔓延，拱顶、拱腰和边墙截面裂缝均为纵向贯通性纵向裂缝，结构整体破坏失稳。

3)两侧填土完成后，在明洞上方铺设EPS板，减载明洞衬砌声发射事件数和位移随系数λ增加而增加，结构各位置处内力减载量斜率呈先增大后减小的趋势。加载完成后，相对未减载明洞，位移和裂缝均未达到加速增长阶段。明洞上方的EPS板有助于缓减结构位移和裂缝发展，避免结构因外荷载过大而提前破坏，减载结构具有更好的延性。