基于统一解的重叠盾构隧道施工引起土体变形研究

魏纲，赵得乾麟，徐浩，周烨波，陈春来

(1.浙大城市学院土木工程系，浙江杭州，310015；2.浙江省城市盾构隧道安全建造与智能养护重点实验室，浙江杭州，310015；3.城市基础设施智能化浙江省工程研究中心，浙江杭州，310015；4.绍兴文理学院土木工程学院，浙江绍兴，312000)

随着城市地铁线路数量不断增加，地铁施工环境将越来越复杂。新建地铁会受到地面、地下建筑物、地质环境、市政管道、既有隧道等多因素的影响难免出现重叠施工的情况。与常见的单线、双线水平平行隧道不同，隧道上下重叠施工会对土体造成二次扰动，且2条隧道或处于不同地层，与其他工况相比土体变形更难预测与控制，对周边建筑安全存在一定威胁。因此，针对重叠盾构隧道施工造成的土体变形开展相关研究具有重要意义。

目前国内外关于盾构隧道施工造成土体变形的研究大多都是围绕单线、双线水平平行工况进行。重叠工况的相关研究主要有：1)基于Peck 公式的经验方法[1-3]；2) 边界单元法[4]；3) 有限单元法[5-7]；4)模型试验法[8-10]；5)现场实测法[1,3]等。现有研究主要以有限单元法进行工况模拟较多，理论方面的研究较少。通过对重叠盾构隧道施工造成土体变形的现有理论研究进行归纳，发现有以下不足之处：现有理论研究大多是对Peck 公式进行修正，但Peck 公式是经验公式且仅能计算地表沉降；现有计算方法仅适用于计算其研究工程的沉降，计算其他工程沉降时与实测结果不够吻合，公式推广使用效果不佳；现有相关理论公式大多仅能计算地表沉降，未发现关于地下不同深度土体沉降以及深层土体位移的理论计算。因此，有必要针对重叠工况的土体变形特别是深层土体位移开展进一步理论研究。

本文作者基于盾构法隧道统一土体移动模型解[11](后文称统一解)，建立计算重叠盾构隧道施工引起的土体沉降公式以及深层土体水平位移计算公式；对深层土体水平位移变化规律进行总结；通过对实际工程案例进行分析计算，本文方法所得计算结果与实测结果、数值模拟结果对比验证本文公式可行性。

1 研究现状

1.1 基于Peck公式的经验方法

PECK[12]统计了大量的实测结果，指出盾构施工产生土体移动是土体损失造成的。通过假设土体不排水、沉降槽体积与土体损失体积相等，提出地表沉降槽呈正态分布，横向地表沉降估算公式为：

式中：S(x)为离隧道轴线x距离处的地表沉降量；x为与隧道轴线的水平距离；Smax为隧道轴线上方最大地表沉降量；i为地表沉降槽宽度系数；Vloss为盾构隧道单位长度的土体损失量；R为隧道开挖半径；η为土体损失率。

由于Peck公式的计算对象为单线隧道，因此，赵帅等[1-3]对该公式进行了修正，提出适用于重叠隧道的修正Peck 公式。相关理论研究方法可分为2种。

方法1：将上下线隧道的地表沉降进行叠加得到总的沉降曲线。赵帅[1]采用叠加原理，将上线沉降与下线沉降相加来算得总沉降曲线，提出沉降公式：

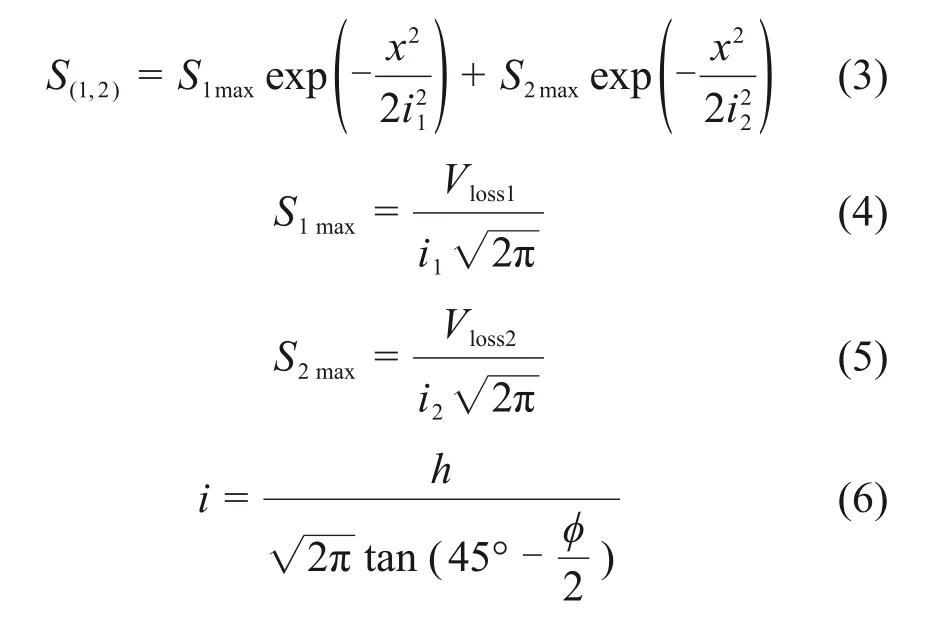
式中：S(1,2)为上下线隧道开挖对地表引起的沉降，隧道1 为上线隧道，隧道2 为下线隧道；Vloss1为隧道1 开挖单位长度的土体损失；Vloss2为隧道2 开挖单位长度的土体损失；S1max为隧道1轴线地表处的最大沉降；S2max为隧道2 轴线地表处的最大沉降；i1为隧道1开挖的地表沉降宽度系数；i2为隧道2开挖地表沉降的宽度系数；h为隧道轴线埋深；φ为土体内摩擦角。

方法2：将重叠隧道等价地看作一个大圆隧道，直接求大圆隧道造成的地表沉降。FANG 等[2]对Peck 公式进行修正，认为总沉降不能单纯将上下线沉降曲线叠加，提出了适用于完全叠落隧道的土体损失率加权计算方法，总沉降计算公式采用Peck 公式即式(1)，土体损失以及沉降槽宽度系数计算方法见式(7)和(8)。

式中：Vloss'为最终计算采用的土体损失率；Vloss为单条隧道开挖时的土体损失率；hmax为很多条隧道中最下方隧道的轴线埋深；hn为除最下方之外的其余隧道的轴线埋深；K为经验参数。

李自锋[3]通过拟合实测结果提出重叠工况施工地表沉降公式，总地表沉降计算方法采用式(1)，沉降槽宽度系数为

式中：h1为上线隧道轴线埋深；h2为下线隧道轴线埋深。

采用Peck 公式计算沉降需要确定2 个重要参数，即Vloss和i，现有研究的参数取值方法如表1所示。

由表1 可知：现有基于Peck 公式的重叠盾构隧道沉降计算方法都只能计算地表沉降，且参数取值方法各不相同。文献[1]的沉降槽宽度系数计算方法已被文献[13]证实是错误的，文献[2-3]中的地表沉降计算方法运用在本文实测结果上效果不好，其原因是2个重要参数取值方法存在问题。此外，Peck 公式是经验公式，且不能计算深层土体水平位移，因此，后续参考Peck 公式进行深层土体沉降以及水平位移的相关研究。

表1 Peck修正公式取值方法Table 1 Valueing methods of Peck's modified formula

1.2 随机介质理论

LITWINISZYN[14]基于砂箱模型试验研究，建立了随机介质理论。该理论是将土体视为“随机介质”，认为开挖造成土体下沉是一种随机的过程，从统计的观点，把隧道开挖造成土体沉降看作无数个小开挖对土体造成的沉降总和，因此，该理论仅能计算开挖隧道上部的土体变形情况，且现有研究大多围绕地表沉降进行开展。该理论运用到地铁隧道开挖引起土体变形的预测中，研究对象包括单线隧道[15-16]，双线隧道[17-18]，双圆隧道[19-20]等。

1)单线隧道。阳军生等[15]基于随机介质理论提出了挤压式盾构隧道施工地表位移预测方法。施成华等[16]应用随机介质理论对隧道施工所引起的纵向土体移动与变形进行了分析，推导了相应的计算公式。

2)双线隧道。魏纲等[17-18]首先基于单线随机介质理论简化公式，提出了双线平行盾构施工引起的地表沉降计算方法，随后考虑沉降曲线的不对称性，提出了近距离双线平行盾构施工引起的地表沉降计算方法。

3)双圆隧道。魏纲等[19-20]先提出了双圆隧道的地表沉降预测方法，随后针对不同工况进行了相关研究，推导出双圆盾构隧道施工时，正常工况和旋转工况下由于土体损失引起的土体沉降计算公式。

1.3 解析解

源汇法由SAGASETA[21]提出，它可以解决线弹性半无限体内由于土体损失而产生的位移场求解问题。把土体损失等价为一个圆柱体，假设它沿着轴线均匀分布，得到在不排水条件下的三维地面变形计算公式：

式中：y为与开挖面的水平距离。该公式未将施工造成的影响考虑在内，无法解释地面隆起现象。后来一些学者对Sagaseta公式进行了修正，针对单线[22]、双线[23]隧道提出了土体位移计算方法。

对于单线隧道，魏纲[22]通过推导得到盾构施工过程中由于土体损失引起的土体变形二维解。双线隧道方面，WEI 等[23-24]基于文献[22]提出了适用于双线平行隧道施工造成土体变形的二维、三维计算方法。

基于源汇法的研究，大多围绕单线、双线隧道进行，关于重叠工况的研究尚未发现。

1.4 不足与改进

本文介绍了现有重叠盾构施工造成土体变形的理论研究，其不足之处可归纳为以下几点：1)Peck公式是经验公式，现有相关研究仅针对地表沉降进行了计算，未对深层土体沉降进行研究计算，不能计算深层土体水平位移；2)未发现关于重叠工况土体变形的随机介质理论计算方法，但该方法只能计算隧道以上部分土体的位移；3)统一解可以计算深层的土体位移，但目前尚未开展重叠工况的研究。

改进方法：针对现有研究方法的不足，本文基于单线盾构土体位移统一解，采用上线、下线叠加得到总沉降以及深层土体水平位移的思路，建立关于重叠盾构施工造成土体沉降以及深层土体位移的计算方法，该方法既能计算不同埋深的土体沉降，又能计算深层土体水平位移。

2 本文方法

魏纲[22]在盾构法隧道统一土体移动模型的基础上，假设土体不排水，参考LOGANATHAN 等[25]提出的研究方法，修正了VERRUIJT等[26]的计算公式，最终得出盾构施工过程中由于土体损失这一因素而产生的土体变形二维解，其中土体竖向位移计算公式为：

式中：z为与地面的垂直向距离，以地面向下为正；h为隧道轴线埋深；d为土体移动焦点到隧道中心点的距离，d=βR，β取值范围为[0,1]；g为等效土体损失参数，且关于统一解的参数取值可参考文献[27]。

统一土体移动模型引起的土体水平方向位移公式为

现有统一解的研究内容主要围绕双线平行工况进行，还未对重叠工况下盾构隧道施工造成的土体扰动进行研究，因此，本文在单线统一解公式的基础上，对重叠工况统一解公式进行推导。

通过对重叠工况实测结果进行分析，可发现重叠工况的地表沉降曲线符合正态分布规律。但重叠工况比双线平行工况要复杂，其原因是在水平平行工况下，隧道处于同一土层，土质情况差别不大，而重叠隧道由于隧道埋深不同，土质存在差别，上下隧道或不在同一土层(见图1)，因此，参数取值存在一定难度。

图1 平行和重叠隧道地质情况示意图Fig.1 Sketch map of geological conditions of parallel and overlapping tunnels

本文在式(13)～(17)的基础上分别计算上下线的地表沉降曲线，采用上下线叠加的方法进行重叠隧道总地表沉降的计算。本文计算公式，重叠工况盾构施工引起总的土体竖向位移为：

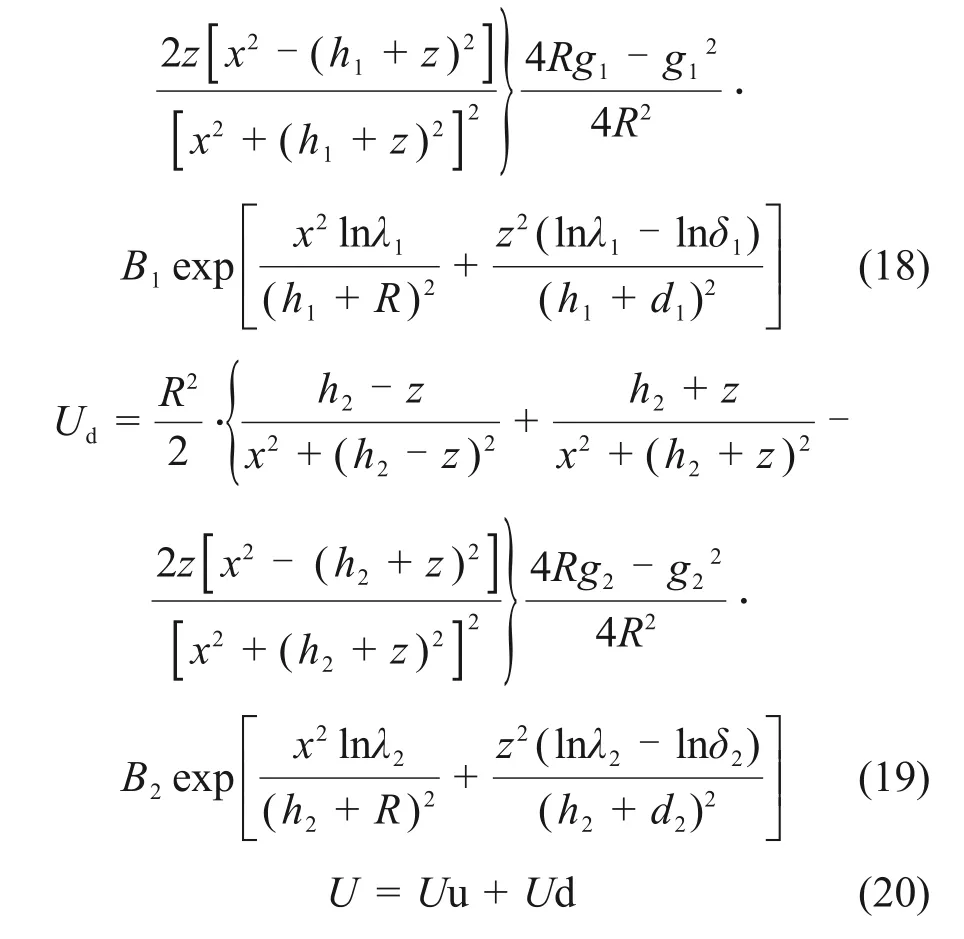
重叠工况盾构施工引起总的土体水平位移为：

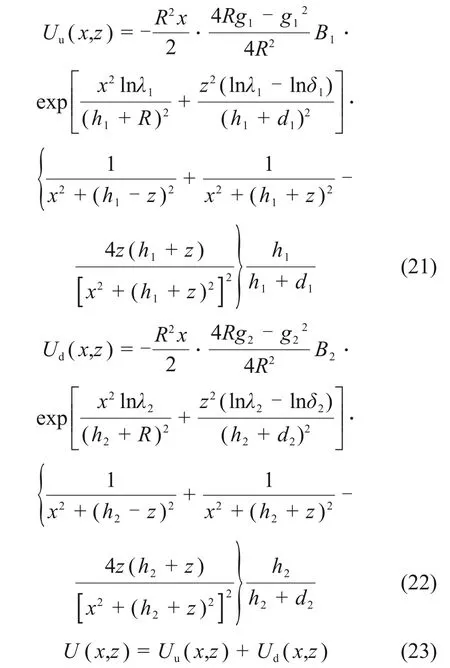
式中：Uu为上线隧道竖向土体位移；Ud为下线隧道土体竖向位移；U为总土体竖向位移；Uu(x,z)为上线隧道水平土体位移；Ud(x,z)为下线隧道土体水平位移；U(x,z)为总土体水平位移；下标1代表上线对应参数；下标2代表下线对应参数；公式中需要确定2 个参数，即土体损失率η以及参数d中的β。

β为移动焦点离隧道轴线距离与隧道外半径之比，它能反映土体性质。关于β的取值，魏纲等[27]已通过对大量工程案例归纳总结，提出其经验取值范围，认为土质条件越密实则取值越大，越松散则越小，一般来说，埋深越深β越大，取值范围为[0,1]。由于重叠隧道施工，先建隧道会对土体造成一定扰动，因此，本文根据工程案例的土体性质以及开挖顺序进行参数取值。本文作者认为，先开挖隧道β的取值应当大于后开挖隧道的β，因为开挖会对土体造成扰动。但这一观点成立的前提是土质条件较密实，若土质极为松散，则β取值越大。由于现有实测结果有限，该观点有待更多数据来进行考证。本文参考文献[27]先得出与本文工程案例土质相匹配的粗略β，再运用Matlab软件进行计算，最终得出与实测结果相吻合的精确值。

关于土体损失率η的取值方法有：1) 反分析法；2)经验取值法；3)理论计算法。由于工程施工过程中造成的土体损失体积难以获取，经验取值存在较大的偏差，采用实测结果反分析来获得土体损失率是最能反映工程实际情况的办法，因此，本文采用反分析法来获取土体损失率。反分析法就是在已有地表沉降实测值的前提下，不断试算η，当计算沉降曲线与实测曲线最吻合时，即可得到最佳值。

综上所述，本文中2 个重要参数取值方法是：基于工程案例的实测地表沉降，先确定粗略的β，再运用Matlab软件对η和β进行大量试算，最终得到与实测沉降曲线最接近的计算沉降。

本文方法与Peck 公式都需要确定2 个重要参数。Peck公式需要确定沉降槽宽度系数i以及土体损失率；本文方法则需要对土体移动焦点到隧道中心点的距离d(d=R·β)以及土体损失率进行取值。忽略二者相同点土体损失率，β可以根据各个工程土体性质进行粗略取值，然后通过计算得出适合相应工程的精确值，而沉降槽宽度系数的取值精度低于本文方法的取值精度。因此，本文方法更能反映工程的实际情况，推广性更强也更适用于工程项目。

3 工程实例

3.1 上海地铁某盾构隧道区间

上海地铁某盾构隧道区间[4]施工顺序为先上线后下线。隧道直径为6.20 m，上线埋深为15.15 m，下线埋深为24.70 m。盾构施工所在土的泊松比v=0.4。由于尚未有关于重叠盾构隧道地下土体位移的实测结果，本文与文献[4]提供的边界单元法计算结果进行对比。根据土体性质以及位移曲线反分析得出土体损失率η1=0.3%和η2=1.8%，以及β1=0.4 和β2=0.2。通过修正后的统一解公式计算该区间的实测结果。当x为10，12 和15 m 时，本文计算值与边界单元法对比结果如图2所示。

图2 x不同时本文计算值与边界单元法结果对比Fig.2 Comparison of results of this paper with boundary element method at different x

本文方法计算结果与边界单元法模拟结果偏差如表2所示。

分析图2及表2可知：本文计算结果与边界单元法模拟结果基本吻合，计算结果偏差最大值为2.84 mm，最大偏差所在深度均为30.00 m处。

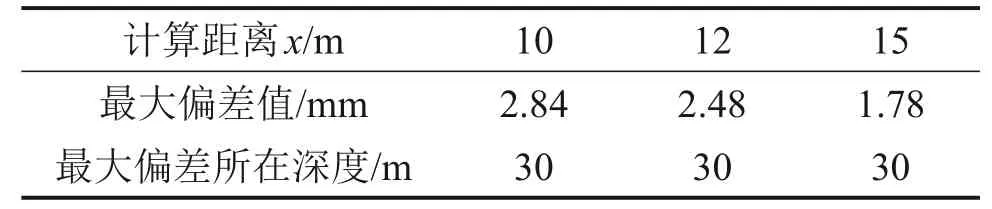
表2 计算结果偏差情况Table 2 Deviation of calculation results

将本文计算方法所得结果与边界单元法模拟结果进行比较可以得出以下结论：重叠盾构隧道施工土体水平位移呈S形，在两隧道之间出现S形的拐点，原因是隧道之间的土体受到2次扰动，故该位置土体位移最大；距离隧道轴线越远，位移越小，原因是距离隧道轴线越近，土体受到的影响最大，因此，土体位移也最大。本文计算结果与边界单元法计算结果基本吻合，说明本文方法可行。

3.2 南宁朝阳广场重叠区间

南宁朝阳广场重叠区间[28]施工顺序为先下线后上线。隧道直径为6.28 m，上线埋深为16.50 m，下线埋深为24.50 m。盾构施工所在地层主要为黏土层、中砂层、圆砾层和泥岩砂岩层，除了少部分外，主要穿越圆砾层和泥岩地层。

根据土体性质以及实测最大沉降可通过反分析得出土体损失率η1=0.77%和η2=1.15%，以及β1=0.5 和β2=0.8。通过修正后的统一解公式计算南宁朝阳广场重叠区间的实测数据，地表沉降计算结果如图3～5所示，深层土体沉降如图6所示。

由图3～5可知：实测结果与计算结果符合正态分布，重叠盾构隧道施工地表沉降形状呈V 形。一些实测结果存在突变的情况，有的地方还出现隆起的现象。造成隆起的因素很多，主要有注浆、盾壳摩擦力、盾构机正面推力等，而本文仅考虑了土体损失，因此，不存在隆起的计算结果。隧道轴线处即x=0 m 时的计算值与实测值一致，上线、下线和总沉降分别为12.6，15.1 和27.7 mm，沉降曲线与实测结果基本吻合。

图3 上线计算结果与实测结果对比Fig.3 Comparison of calculation results with measured results of upper tunnel

由图6可知：重叠盾构隧道施工造成的土体沉降从地表到深度12 m 处缓慢增大，深度接近上线隧道拱顶时沉降激增，最大值在上线隧道拱顶处。其原因是隧道开挖对土体造成一定扰动，而隧道周边土体受到扰动最大，因此，最大沉降出现在上线隧道拱顶处。由于尚未发现重叠工况深层土体沉降的相关研究以及实测结果，故无法将本文计算结果与相关结果进行对比。

图4 下线计算结果与实测结果对比Fig.4 Comparison of calculation results with measured results of lower tunnel

图5 总沉降计算结果与文献[28]中实测结果对比Fig.5 Comparison of total settlement calculation results with measured results in Ref.[28]

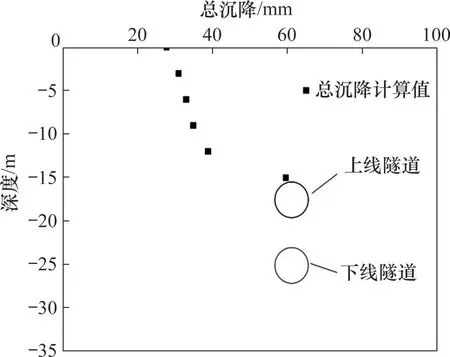
图6 隧道轴线上方土体沉降Fig.6 Ground settlements above tunnel centerline

通过式(21)～(23)计算土体水平位移，距离轴线6 m 和9 m 的水平位移计算曲线分别如图7～9所示。

图7 上线隧道在6 m和9 m时的土体水平位移Fig.7 Horizontal displacement of soil mass of upper tunnel at 6 m and 9 m

由图7～9 可知：盾构隧道地下土体位移呈现S形，单线位移在隧道所在深度附近位移最大，总位移曲线与单线隧道水平位移曲线基本一致，呈S形，在隧道所在深度附近位移最大。

图8 下线隧道在6 m和9 m时的土体水平位移Fig.8 Horizontal displacement of soil mass of lower tunnel at 6 m and 9 m

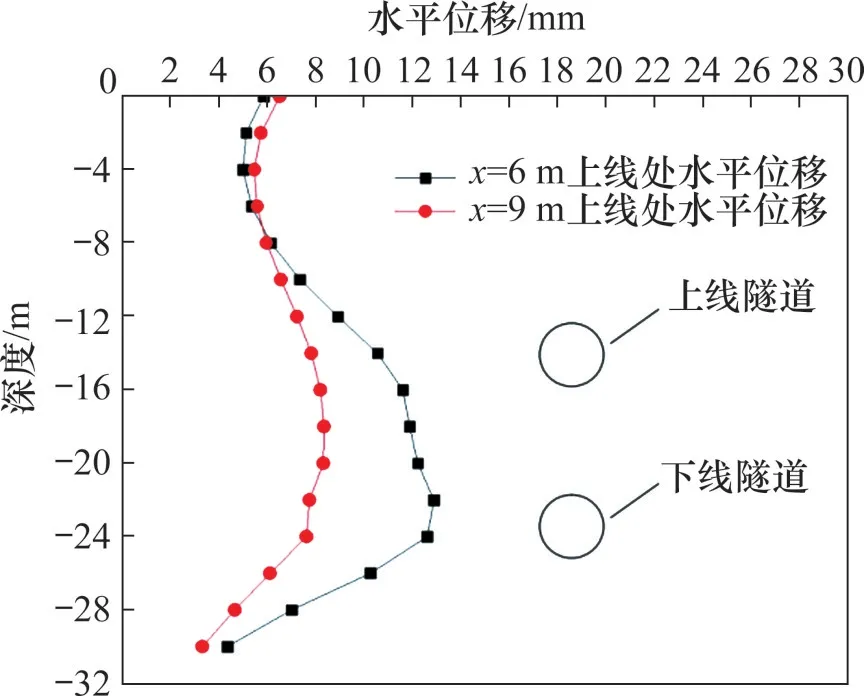
图9 总土体水平位移曲线Fig.9 Total horizontal displacement of soil mass

3.3 深圳地铁三号线重叠隧道区间

深圳地铁三号线重叠隧道区间[29]施工顺序为先建上线后建下线。隧道直径为6.0 m，上线埋深为10.6 m，下线埋深为18.2 m。盾构施工所在地层主要为粉质黏土层、洪积中粗砂层，主要穿越中粗砂地层。

本文根据土体性质以及实测总沉降曲线反分析得出土体损失率η1=0.35%和η2=1.85%，以及β1=0.15 和β2=0.25。通过修正后的统一解公式计算该区间的实测结果。由于只有该工程总地表沉降的实测结果，因此，本文只针对总地表沉降的计算结果和实测结果进行比较，对比结果如图10所示。

由图10 可知：统一解重叠公式计算得出的沉降曲线与实测曲线基本吻合，隧道轴线处地表沉降实测值与计算值一致，当x=2 m时，最大偏差为-2 mm。

图10 总沉降计算结果与文献[29]中实测结果对比Fig.10 Comparison of total settlement calculation results with measured results in Ref.[29]

4 结论

1)基于Peck 公式的经验方法尚未提出通用的计算方法，一些学者提出的计算方法不适用于其他实测结果。其原因是现有研究未能提出一个合适的取值方法计算各种工程的沉降槽宽度系数，且该公式为经验公式，由于一些地区的数据不够完善，所以，难以计算出准确的地表沉降；目前随机介质理论尚未用于重叠工况的理论研究。

2)本文基于盾构法隧道统一土体移动模型解，建立重叠盾构施工引起的土体变形解析解，并提出重叠隧道施工引起的深层土体水平位移计算公式。分别计算上、下线隧道引起的土体变形，然后叠加得到重叠盾构施工引起的总的土体变形。通过对比可知，本文计算结果与实测结果、边界单元法结果较吻合，说明本文方法可行。

3)重叠盾构隧道施工地表沉降曲线符合正态分布规律，沉降曲线呈V 形；深层土体水平位移呈S形，土体位移最大值在隧道埋深位置附近；深层土体沉降从地表到拱顶附近缓慢增大，深度接近上线隧道拱顶时沉降激增，最大值在上线隧道拱顶处。

4)由于重叠隧道处于不同的埋深，需要采用不同的η和d。本文公式中的η和β取值采用反分析法，与传统的经验取值方法相比更能接近实测结果。后续将对参数取值进行深入研究，建议进行大量的数据搜集从而得出更精准的取值范围。

5)由于本文仅考虑土体损失，计算结果与实测结果存在一定差异，后续研究可以考虑盾构隧道施工过程中影响土体变形的诸多因素，如对同步注浆、掘进速度等方面进行深入研究。本文研究的计算方法属于重叠盾构隧道施工造成土体变形的二维计算方法，后续研究可以将二维解计算方法拓展为三维解计算方法。