TDA与底砟混合物耗能特性试验研究

陈晓斌，吕金，丁瑜，朱禹，张俊麒，肖源杰，魏丽敏

(1.中南大学土木工程学院，湖南长沙，410083；2.中南大学教育部重载铁路工程结构重点实验室，湖南长沙，410083)

随着大轴重、高牵引量重载列车的快速发展，道床所承受的动荷载强度和疲劳作用更大[1-4]，过大的动应力加速了道砟颗粒的磨耗粉化，磨耗形成的细小颗粒在水的作用下易形成道床脏污，进而削弱了道床的弹性、降低了道床的排水性能，导致行车安全性和舒适性下降。另一方面，随着环保意识的强化，废旧汽车轮胎颗粒(tire derived aggregate，TDA)已应用于土木工程领域。相比于传统的土工材料，TDA 具有质量轻、弹性变形能力强、剪切模量低、能量吸收能力优良等特点[5-6]。有学者将TDA 直接加入到底砟材料中，用来减小铁路道床振动与底砟颗粒的磨耗，由此形成TDA与底砟混合料。

HIDALGO SIGNES 等[7]通过现场试验研究了底砟与TDA 混合物的振动特性，评估混合物对列车引起的道床振动减弱效果，结果表明：TDA 含量越高，由车辆荷载引起的道床振动减轻越明显。MARTÍNEZ FERNÁNDEZ 等[8]在现场建立了3 条30 m 长的试验段，探究了底砟与TDA 混合物的动力响应，结果表明，随着TDA 含量的增加，加速度峰值明显减小，体现了TDA 的减振效应。此外学者们在实验室也开展了一些道砟与TDA 混合物的土工试验。ESMAEILI 等[9-11]将TDA 与道砟混合，对混合料的动力性质进行了室内试验，研究表明：道砟与TDA混合料的刚度随TDA含量的增加有明显的减小，而阻尼比有明显的增大。SOL-SÁNCHEZ 等[12]通过道砟箱动力试验探究TDA 与道砟混合物的动力性质，其结果表明TDA的加入减少了道砟的颗粒破碎，降低了道砟的刚度，提升了道砟的阻尼比。QI等[13-14]通过循环三轴试验研究了TDA含量对钢渣和煤矸石混合物应变、回弹模量、阻尼比以及剪切模量等的影响，结果表明：TDA 的加入增加了混合物的轴向应变、体积应变、阻尼比以及能量吸收能力，减小了混合物的回弹模量和剪切模量。

以上研究表明：道床中加入TDA 可以增加道床的弹性，从而减弱道砟颗粒破碎的程度，降低基床层的动力响应。但是目前TDA 在道砟中的应用主要集中于现场试验，在实验室中受限于道砟的尺寸和试验仪器，呈现的结果不具有一致性，且对其在动力作用下应力-应变关系、回弹模量、耗散能等特性缺乏统一有效的结论。为此，本文作者采用能真实模拟底砟材料实际受力状态的大型三轴仪开展TDA与底砟混合物耗能性质的研究，旨在探究TDA 与底砟混合物的磨耗性能以及减振耗能特性，确定最优TDA体积分数，为TDA与底砟混合物的实际工程应用提供借鉴。

1 试验材料与方法

1.1 试验材料

试验材料有级配碎石(重载铁路底砟层材料)和废旧汽车轮胎颗粒，试验材料照片如图1所示。底砟材料购于长沙某矿石厂，主要成分为花岗岩，大部分颗粒棱角分明，近似立方体，硬度较大。TDA购于长沙某汽车修理厂，其内部钢丝被剔除，加工成碎颗粒状。

图1 试验材料照片Fig.1 Photos of subballast particles and TDA particles

试验材料的物理力学参数见表1，各试样的级配曲线见图2。图中，d10，d30，d50和d60分别为累积质量分数为10%，30%，50%和60%时对应的粒径；Cu为不均匀系数；Cc为曲率系数。从图2可见：底砟粒径范围为0.1～25.0 mm，不均匀系数为24.2，曲率系数为2.12，属于级配良好的粗颗粒骨料，级配曲线符合TB/T 2897—1998“铁路碎石道床底砟”的级配要求。TDA粒径范围为7～9 mm，颗粒相对密度为1.33。

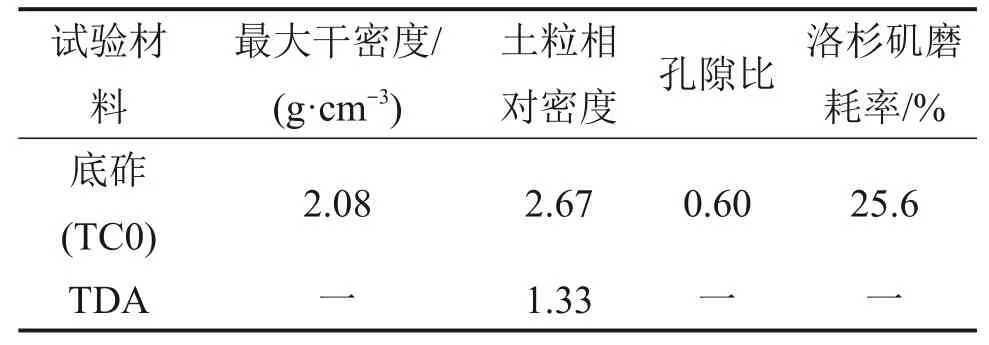
表1 试验材料的物理力学参数Table 1 Basic physical parameters of tested materials

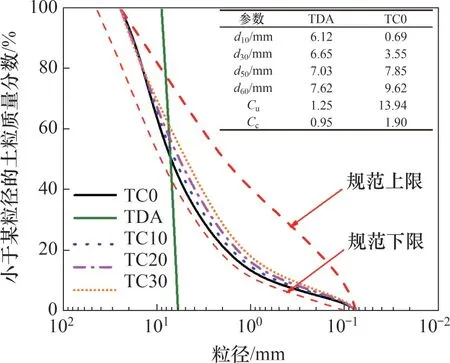
图2 试验材料的级配曲线Fig.2 Grain-size distribution curves of tested materials

为研究TDA掺量对底砟材料耗能特性的影响，配置TDA 体积分数分别为10%，20%和30%的3种TDA 与底砟混合物试样，各试样编号及其物理参数如表2所示。

表2 TDA与底砟混合物的物理力学参数Table 2 Basic physical parameters of TDA-subballast mixtures

为分析TDA 体积分数对底砟颗粒磨耗性能的影响，进行了洛杉矶磨耗试验。试验结束后，按照式(1)计算洛杉矶磨耗率：

式中：LA为洛杉矶磨耗率；m1为试样磨耗前的质量，g；m2为试样磨耗后粒径大于1.7 mm的颗粒质量，g。

混合物洛杉矶磨耗率随TDA 体积分数的变化见表2。从表2可以看出：随着TDA体积分数的增加，其磨耗指数迅速下降，其关系近似线性。纯底砟的洛杉矶磨耗率约为25.6%；当TDA 的体积分数为10%时，混合物的洛杉矶磨耗率约为20.1%，比纯底砟的洛杉矶磨耗率下降了21.5%；而当TDA 的体积分数为30%时，混合物的洛杉矶磨耗率约为11.2%，下降了56.3%。分析原因认为：TDA 作为一种弹性元件，与底砟颗粒之间为柔性接触，TDA 的加入能够吸收一定能量，增加底砟的弹性，降低底砟与底砟之间的刚性碰撞，从而使其洛杉矶磨耗率降低，在一定程度上抑制了底砟之间的颗粒破碎。

1.2 试验仪器

试验采用DXSZ-150大型动静三轴试验仪，该仪器主要由主机、三轴仪、液压水源和轴压油源、电控系统、计算机及软件系统等部分组成。

1.3 试验方法

1.3.1 试验方案

INDRARATNA等[15]指出道床围压为1～240 kPa，YU[16]的研究认为道床围压为20～200 kPa，本文设定围压为50 kPa。选用正弦波加载方式以模拟循环列车荷载的作用，研究表明，列车荷载引起的有砟道床振动频率为0.1～20 Hz 之间，以1～2 Hz 为主[17-21]，因此，本文设定加载频率为1 Hz。另外，BIAN 等[22]指出列车荷载作用在轨枕和道床接触面处的最大动应力与列车轴重、行驶速度、轨枕长度以及轨枕宽度等因素有关，对于轴质量为25 t、以80 km/h运行的重载列车，其轨枕和道床接触面上的最大动应力约为200 kPa。因此，本文设定动荷载幅值为200 kPa，动力循环次数为20 000 次。此外，轨道上部结构具有一定的质量，且该质量不能以循环荷载的方式施加，因此，在试样轴向额外施加25 kPa的预载。每种试样进行3个平行试验，结果取平均值。

1.3.2 试样制备

试样的直径×高为300 mm×600 mm，试样采用击实法制备。首先，在清洗干净的压力室底座上固定厚度约为2 cm的橡皮膜，保证橡皮膜不漏气、不渗水；然后将对开半圆制样筒安装好，并将橡皮膜贴紧制样筒；最后，根据不同试验工况以及TDA 底砟混合物的最大干密度和压实度计算得到每组试样需要的TDA 质量和底砟质量，将配置好的材料均匀混合，分5次加入制样筒中击实，击实过程中应尽量控制相同的击实能量，每层的击实次数保持一致；在进行下一层压实之前，要将上一层已经压好的土样刨毛，以保证各层之间的良好接触。

制备好的试样采用真空抽气饱和以及冲水饱和相结合的方式进行饱和，当孔压系数≥0.98 时，试样饱和完成。

按照设定的围压进行试样固结，固结过程中打开上下排水管，当30 min 内试样排水量不超过15 mL时，即可认为试样固结完成，固结完成后关闭上下排水阀门开始进行试验。

2 试验结果分析

列车运行过程中产生的能量一部分被底砟层吸收，另一部分传递至路基结构层。被底砟层吸收的能量一部分转化为底砟的轴向应变和体积应变，另一部分以底砟颗粒间的摩擦耗能和回弹变形的形式被耗散[23-24]。为此，本文基于能量传播角度，通过大型动三轴试验分析TDA 体积分数对底砟材料轴向应变和体积应变、动应力-动应变滞回曲线、回弹模量以及耗散能的影响规律。

2.1 轴向应变和体积应变

TDA 与底砟混合物轴向应变随振动次数N的变化曲线如图3 所示。从图3 可以看出：在N＜200时，试样处于初期压密状态，小颗粒填充在大颗粒孔隙中，轴向应变增长速率较大，此时试样产生的变形基本是塑性变形。当N＞200 时，试样达到了一定的密实状态，轴向应变的增长速率逐渐降低，此时试样的变形由压密和剪切共同产生。当N＞5 000 时，轴向应变的增长速率达到稳定状态，之后，试样轴向应变以该速率继续增大直到试验结束。随着TDA 体积分数增加，TDA 与底砟混合物轴向应变逐渐增大，且增长速率亦随之增大。这是因为，TDA 的刚度较小，变形较大，当TDA 体积分数较高时，混合物刚度降低明显，因此产生较大的轴向应变。

图3 TDA与底砟混合物轴向应变随振动次数变化曲线Fig.3 Curves of axial strain vary with vibration times for TDA-subballast mixtures

道砟轴向变形随振动次数变化形式为对数型，其关系式[25]为

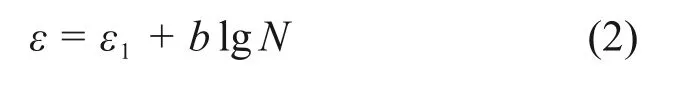
式中，ε为第N次循环荷载作用下的道砟轴向应变；ε1为第一次振动后道砟的轴向应变；b为经验系数。

利用式(2)对各组试样的轴向应变与振动次数变化曲线进行回归分析，得到的拟合参数以及相关系数见表3。从表3 可以看出，对数模型能较好地反映TDA 与底砟混合物轴向应变随振动次数的发展规律。

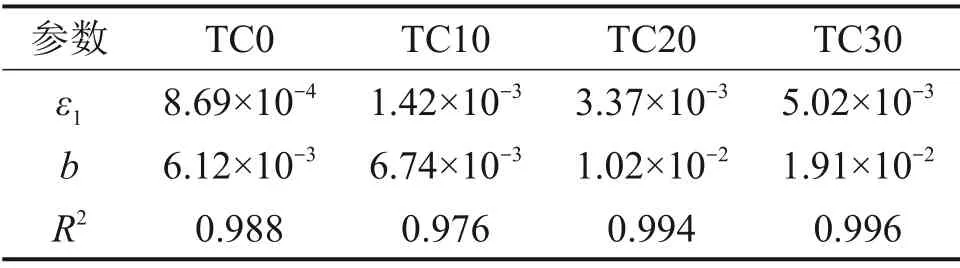
表3 各组试样的轴向应变与振动次数变化曲线拟合参数Table 3 Fitting parameters of curves of axial strain vary with vibration times for TDA-subballast mixtures

体积应变反映了试样在循环加载过程中的稳定性状况。TDA 与底砟混合物体积应变随振动次数N的变化曲线如图4所示。从图4可以看出：随着振动次数增加，不同TDA 体积分数试样的体积应变均表现为减少，当N＜3 000时，试样体应变增长迅速，当N达到10 000时，体积应变的增长速率减小，表明试样在此时基本达到了密实状态。随着TDA体积分数增加，试样的体积变形逐渐增大，这同样是由于TDA 的加入增大了试样的变形能力。

图4 试样体积应变随振动次数变化曲线Fig.4 Curves of volumetric strain vary with vibration times for samples

2.2 动应力-动应变滞回曲线分析

将一个振动周期内的动应力随动应变变化的曲线绘制成图，即可得到动应力-动应变滞回曲线。图5 所示为振动次数N分别为10，100，1 000，10 000和20 000时不同试样的动应力-动应变滞回曲线。从图5 可知：试样的动应力-动应变滞回曲线均近似呈梭型，当N≤10时，振动初期滞回曲线的高度均略小于后期振动产生的滞回曲线的高度，说明此时试样受到的动应力并没有达到设定的动应力幅值，振动初期试样处于不稳定状态，此时，不同TDA体积分数试样的动应力-动应变滞回曲线均没有闭合，试样的塑性应变较大，这是由于试样的初始孔隙率较大，当振动开始时，试样迅速被压密，产生较大的塑性变形。随着振动次数的增加，TDA与底砟混合物的动应力-动应变滞回曲线逐渐闭合，动应力幅值基本保持稳定，当N为10 000和20 000时，滞回曲线基本重合，说明N＞10 000 时，试样达到相对稳定状态。从滞回曲线移动的距离来看，随振动次数增加，试样轴向应变逐渐增大，但增长速率逐渐降低。

图5 不同振动次数下试样动应力-动应变滞回曲线Fig.5 Stress-strain hysteretic curves for samples at different vibration time

为了分析TDA 体积分数对混合物滞回曲线形状的影响，将不同TDA 体积分数的试样在10 000振动次数下的滞回曲线顶点移动至同一点。当N=10 000 时，试样滞回曲线随TDA 体积分数变化如图6所示。从图6可以看出：随着TDA体积分数增加，动应力-动应变滞回圈逐渐向横坐标轴倾斜，说明其回弹变形逐渐增大，这是由于TDA 的加入使混合物的弹性变形能力提升。随着TDA 体积分数增加，滞回圈逐渐变得圆润，并且滞回圈的面积逐渐增大，说明其耗散能增大，反映其能量吸收能力的提升。

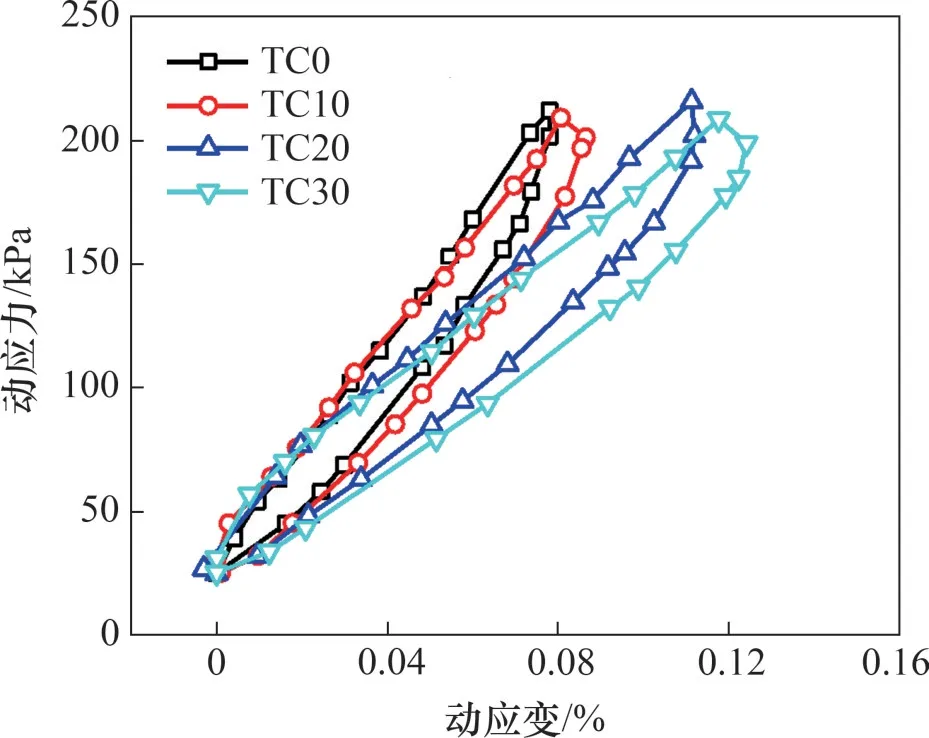
图6 N=10 000时试样滞回曲线随TDA体积分数变化Fig.6 Hysteretic curves for samples vary with TDA volume fraction at N=10 000

2.3 TDA与底砟混合物回弹模量分析

循环荷载作用下物体产生的弹性应变和塑性应变如图7所示。TDA与底砟混合物在循环荷载下产生的轴向应变由可恢复的弹性应变εr和不可恢复的塑性应变εp组成。回弹模量定义为

图7 循环荷载作用下产生的弹性应变和塑性应变Fig.7 Elastic strain and plastic strain under cyclic loading

式中：MR为回弹模量；qcy为动力试验中施加的动应力。

TDA 与底砟混合物回弹模量随振动次数N的变化曲线如图8所示。由于底砟颗粒在动荷载作用下发生颗粒间的错动，因此试验得到的回弹模量会有一定的波动，但能看到清晰的发展规律。TDA 与底砟混合物回弹模量随振动次数的变化可以分为2个阶段：第一阶段，振动导致试样密实度提升，回弹模量随振动次数逐渐上升；第二阶段，当试样达到一定的密实度后，回弹模量保持不变或有缓慢增加。

图8 TDA与底砟混合物回弹模量随振动次数变化曲线Fig.8 Curves of resilience modulus vary with vibration times for TDA-subballast mixtures

回弹模量随振动次数的变化情况可以反映TDA 与底砟混合物的变形机制。虽然试样是以90%的压实度制样，但试样内部仍有较大的孔隙，在加载初期，在轴向荷载作用下，颗粒发生旋转和重排列，部分颗粒填充在大颗粒之间的孔隙中，此时发生的应变主要是塑性应变。随着循环的发展，试样逐渐变得密实，颗粒移动减少，变形主要产生于颗粒之间的接触变形，回弹变形逐渐稳定，试样主要表现出弹性的动力响应。随着TDA体积分数增加，TDA 与底砟混合物的回弹模量下降，这是由于振动荷载作用下TDA 发生的变形几乎都是弹性变形，导致试样回弹变形增大，回弹模量降低。

从上述研究可以看出，TDA 与底砟混合物经过列车荷载长期作用后，回弹模量基本上趋于一种稳定的状态，对于长期承受循环荷载的底砟层，确定其稳定后的回弹模量对道床的设计具有重要的意义。本文以循环次数为20 000 次时的回弹模量为其最终回弹模量。TDA 与底砟混合物最终回弹模量随TDA 体积分数变化曲线如图9 所示。从图9可以看出：TDA与底砟混合物的最终回弹模量随着TDA 体积分数的增加迅速下降，TDA 体积分数为10%～20%之间时，回弹模量降低最为显著。

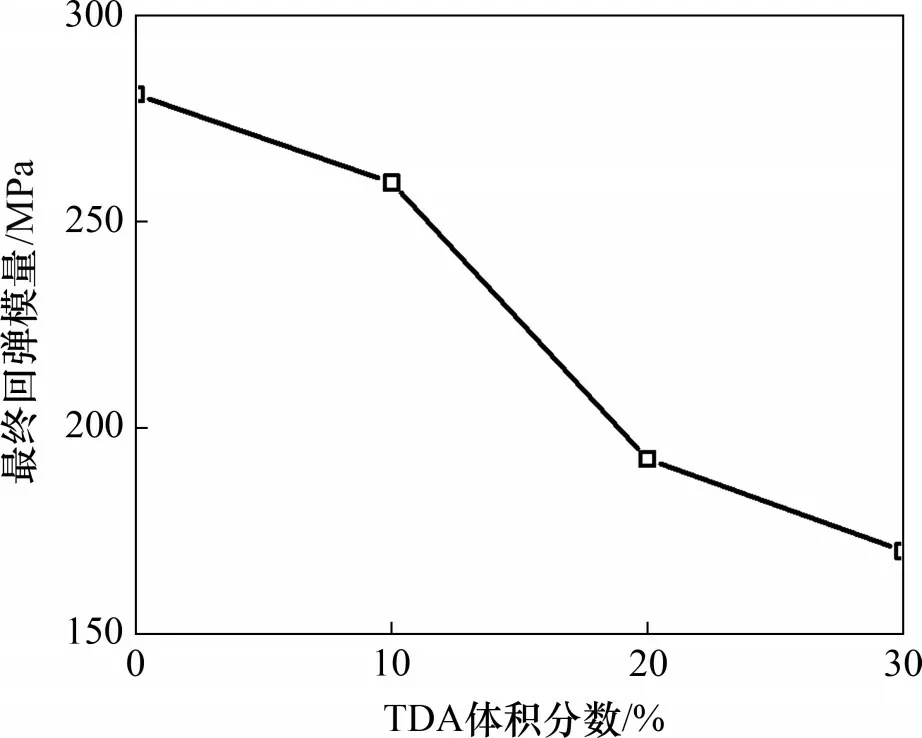
图9 TDA与底砟混合物最终回弹模量随TDA体积分数变化曲线Fig.9 Curve of final resilience modulus for TDAsubballast mixtures vary with TDA volume fractions

2.4 TDA与底砟混合物能量耗散分析

由动三轴试验得到的动应力-动应变滞回曲线可以计算土体的耗散能。耗散能表示动荷载作用下能量耗散的性质，近似等于滞回曲线围成的面积。

TDA 与底砟混合物耗散能随振动次数变化曲线如图10所示。从图10可以看出：随振动次数增加，耗散能逐渐降低，在N＜100 时，衰减明显，随后缓慢降低并在N＞10 000 时基本趋于稳定值。这是由于随着振动次数增加，试样的稳定性逐渐提升，颗粒之间的排布更加紧密，能量波在传播过程中衰减的程度降低，耗散能也基本不再变化。随着TDA 体积分数增加，TDA 与底砟混合物的耗散能逐渐上升：底砟材料TC0的耗散能稳定值约为19.89 J/m3，TC10耗散能稳定值约为25.75 J/m3，比TC0 的提高了约29.5%；TC20 的耗散能稳定值约为34.45 J/m3，提高了约73.2%；TC30 的耗散能稳定值约为40.54 J/m3，提高了约103.8%。说明在底砟中加入一定量的TDA 能显著提升底砟的能量耗散性质。

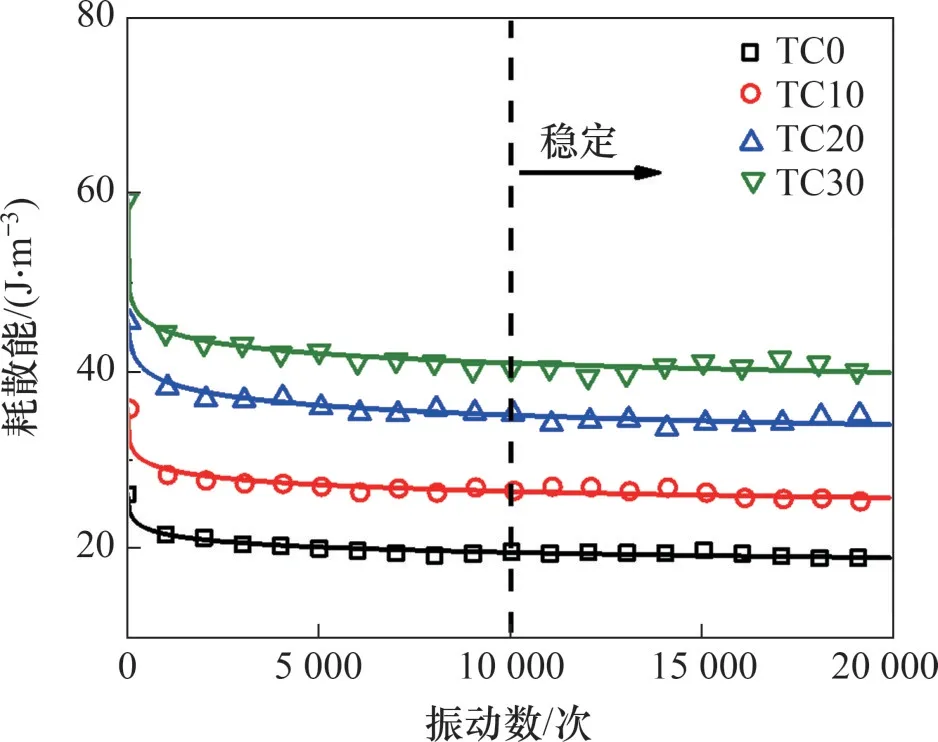
图10 TDA与底砟混合物耗散能随振动次数变化曲线Fig.10 Curves of dissipated energy vary with vibration time for TDA-subballast mixtures

3 配比优化与讨论

以上分析可以看出，在底砟中加入TDA 可以使底砟层有更好的能量耗散能力，能降低底砟的颗粒破碎。但是加入TDA后，由于TDA的低刚度和高弹性变形使底砟的回弹模量降低，在循环荷载作用下变形增大，若在有砟轨道中使用TDA，需要确定既不影响轨道正常使用且能发挥TDA 优势的最优含量。

根据文献和规范[12,26]，评估底砟材料性能的参数及其允许取值范围见表4。轴向应变和回弹模量降低率随TDA体积分数变化如图11所示。从图11可以看出：若满足底砟层变形和刚度需求，TDA体积分数不能超过13%。TDA 体积分数超过13%时，混合物的轴向应变将超过2%，此时不能满足有砟轨道底砟层变形需求。本试验中，满足底砟层变形和刚度要求的TDA 最优体积分数为10%，相比于纯底砟材料，TC10 的能量耗散能力增强，颗粒破碎程度降低，参数变化情况如表5所示。

表4 用于评估底砟的参数和其允许范围Table 4 Parameters for evaluating subballast and allowable range

图11 轴向应变和回弹模量降低率随TDA体积分数变化Fig.11 Curves of axial strain and rate of resilience modulus reduction with different TDA contents

表5 TC10试样参数与底砟参数对比Table 5 Comparison of parameters of TC10 sample with that of subballast

4 结论

1)随着TDA体积分数增加，TDA与底砟混合物的洛杉矶磨耗率LA近似呈线性减小，相比于纯底砟材料，TDA 体积分数为10%的混合物的LA下降了21.5%，TDA 体积分数为30%的混合物的LA降了56.3%。这表明了TDA 的加入能够吸收一定的能量，增加混合物的弹性，进而抑制底砟的颗粒破碎。

2)随着TDA 体积分数增加，混合物的轴向应变和体积应变增大，并且TDA 与底砟混合物的轴向应变随振动次数的发展规律符合对数模型。TDA 与底砟混合物的回弹模量随着TDA 体积分数的增加而下降。

3)相较于纯净底砟的耗散能稳定值，体积分数为10%的混合物的耗散能稳定值提高了约29.5%；体积分数为30%的混合物的耗散能稳定值提高了约103.8%。说明TDA 的加入能显著提升混合物的能量耗散能力。

4)满足底砟层变形和刚度要求的最优TDA 体积分数为10%左右，此时，TDA 与底砟混合物的变形、刚度均能满足要求，并且能够有效抑制底砟的颗粒破碎，具有良好的减振耗能效果。