基于ZIP模型的供水管网灰口铸铁管爆管预测

杨玉龙，何凯军，季京宣，谭洋，徐圣兰，张可佳

(1.浙江大学建筑工程学院，浙江杭州，310058；2.浙江华云电力工程设计咨询有限公司，浙江杭州，310014)

供水管网逐渐老化以及各种环境与人为因素会使城市供水管网产生漏损和爆管现象，这一问题影响了人们的生产生活，更严重威胁到给水工程中最基本的安全问题，因此，预测并及时解决供水管道爆管问题成为行业急需解决的问题。

一般而言，预测城市给水管道爆管现象的模型大致可以分为6种：确定性模型、统计模型、概率模型以及智能算法中的人工神经网络算法、模糊逻辑算法和启发式算法[1]。当存在大量管道基础信息及其爆管历史数据时，可以应用统计学模型，通过回归分析进行爆管预测。统计学模型主要分为3类：简单线性或指数回归模型、广义线性模型及风险比例模型。WALSKI 等[2]提出了改进的时间指数回归模型。YAMIJALA等[3]比较了时间线性模型、时间指数和广义线性模型在预测管网爆管的应用结果，提出并确定了Logistic广义线性模型在爆管预测的运用。卿小飞等[4]也采用Logistic 广义线性模型建立了供水管网爆管预测模型。JEFFREY[5]提出利用风险比例模型预测供水主干管的爆管。近些年，王袆等[6]采用生存分析的方法建立爆管预测模型，柯庆等[7]结合生存分析与风险比例模型建立爆管风险评估模型，陈能等[8]则采用Cox 比例风险模型建立爆管风险预测模型。然而，线性或指数模型假定各组中所有管道爆管服从统一分布且为齐次函数，与实际情况不符，并且因素变量的选择和分类对结果影响很大，通常只用于探究某因素是否影响爆管发生。广义线性模型，例如Logistic广义线性和Poisson回归模型，主要适用于离散型数据。Logistic 模型为了避免过拟合和欠拟合往往需要尽可能考虑所有重要变量，同时需要较大的样本量，并为提高预测精度要对数据进行严格分组。Poisson 回归是计数资料统计分析的首选模型，而当数据中零的比例超过了其对零事件的预测，对于这种特殊结构的计数资料Poisson 回归往往低估事件中的零事件发生概率[9]。风险比例模型的应用需要有丰富的技术经验，同时该模型假定各静态变量以相同比例降低或提高所有管道的爆管风险，与现实情形存在差异。

根据是否影响正常社会活动而需要相关部门尽快维修，可将爆管定义为：在自然因素影响下导致管道结构发生破坏，造成管道内有压水大量冲出地面并需要相关部门及时维修的事故。在计数资料中将有爆管发生的情况记为“1”，没有爆管发生的情况记为“0”，即零观测值。以此来统计数据，则以下情况虽然在统计数据上体现为“0”，但对爆管统计有一定影响：

1)爆管后维修但因为某些情况未记录；

2)管道结构破裂漏失量大，但地面无明显水冲出的痕迹；

3)旧管道被遗弃不用。

由于以上情况，在历史统计数据中无法区别零值的具体原因，从而观察到爆管次数分布中出现了零过多(零膨胀)现象。因此在模型预测过程中需要对过多的零值进行有效处理，以避免偏差过大的参数估计和推断。为了拟合零膨胀这一现象，LAMBERT[10]提出零膨胀泊松(Zero-inflated Poisson，ZIP)模型。目前，零膨胀泊松模型已经被应用于生态坏境[11-12]、医药卫生[13-14]、经济金融[15-16]、交通事故[17-18]等诸多领域中，均得到了较好的应用，但是还未有文献结合ZIP模型对供水管网爆管预测进行研究。

由于用于给水管网的不同管道材质的力学性能不同，管材受力复杂，相关爆管影响因素不清晰，而灰口铸铁管使用历史久、爆管数据量大，适用统计学模型分析，因此，本文作者采用单一灰口铸铁管材为主要研究对象，首先根据不同的爆管影响因素，获取供水管网灰口铸铁管的基本数据及爆管记录，得到所需数据集，其次对数据集进行爆管影响因素描述性统计与过离散检验，然后采用ZIP模型进行参数估计，通过分析爆管数据集验证模型的适用性并复验零膨胀现象，建立爆管数据预测模型，最终构建基于ZIP模型的爆管预测模型，并对爆管预测模型的预测效果进行检验。

1 爆管预测模型的构建

泊松(Poisson)分布是实际离散数据分析中最常用的模型，泊松回归是计数资料统计分析的重要模型，一般要求事件的发生相互独立，事件的条件均值等于条件方差。而在实际情况中，爆管的次数这一计数资料含有过多的零观测值，这可能导致模型参数估计结果与实际情况偏差较大，也使得方差大于均值。由于爆管发生频数呈现出明显的零膨胀现象，因此，本文拟采用ZIP模型对供水管网灰口铸铁管爆管计数资料进行分析，同时对分析数据进行零膨胀检验，根据ZIP模型参数估计结果构建爆管数据预测模型，用于预测某区域某时间管道爆管总次数。

1.1 Poisson回归模型

泊松(Poisson)分布的一般形式如下：

其中：p为概率；Y为随机变量；y为随机实验成功次数；λ为期望值；x为协变量；φ为待拟合系数。

泊松(Poisson)分布的期望和方差为

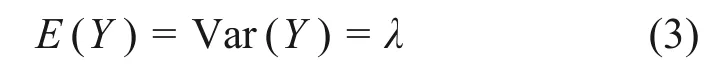
1.2 过离散检验

当爆管数据集的均值和方差相差不大时，即可认为爆管数据集满足泊松分布，否则认为数据存在离散现象，因此，判断数据集是否存在离散现象等价于检验样本方差S2是否等于样本均值Xˉ。

通过计算DE OLIVERA[19]提出的O统计量检验过离散，指出在原假设成立的条件下，O统计量近似服从标准正态分布，即：

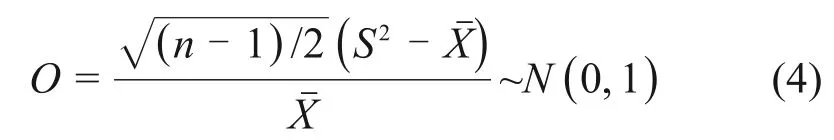
式中：n为样本个数；S2为样本方差；为样本均值。

当计算得到的O统计量大于1.96 时，即可在95%显著性水平下拒绝原假设，认为该数据样本存在过离散现象。

1.3 零膨胀泊松(ZIP)模型

ZIP模型的基本思想是认为计数随机变量来自2个过程：其中一个过程是零事件的发生，假定服从二值概率分布，此时观测值只为零(称为结构零，产生概率为Gi,t)；另一过程对应事件发生的次数，符合一个以概率(1-Gi,t)且均值为λi,t出现的Poisson分布，即满足式(1)中y=0，这部分得到的零观测值为抽样零。ZIP 模型是针对这2 个过程建立的混合概率分布。

根据观测到的供水管网灰口铸铁管的爆管数据可知现实中只有极少数供水管道会发生爆管，即观察到的大部分管道的爆管次数ki,t=0。当实际事件中含有大量零变量时，这组数据并不能很好地服从Logistic 或者泊松(Poisson)分布，考虑应用ZIP模型来解决这个问题。

根据ZIP 的定义，ki,t=0 点为混合分布，而把ki,t＞0 处作为零截断泊松分布，因此得到ki,t次爆管概率可以表示为：

其中：i=1，2，…，N；N为样本中管道总数；t=1，2，…，T；T为爆管记录时间；Gi,t为结构零产生的概率，取值范围为[0，1]；α0为回归方程常数项；α，β和γ为待拟合的系数向量；zi为静态变量，如管材、管径等；pt为动态变量，如管龄、降雨等；qi,t为动静态变量，如历史爆管率、阴极保护等。

为了增加预测精度，假定Gi,t满足Logistic 分布，并且受到爆管期望λi,t的影响，则

其中：g0为ZIP模型待估参数。

从式(7)可以看出，当λi,t逐渐变大时，Gi,t趋向于0，当Gi,t为0 时，则ZIP 模型退化为泊松(Possion)模型；而λi,t逐渐变小时，Gi,t趋向于某一常数。此时，爆管的均值和方差分别变为：

同时，易知ZIP模型的对数似然函数为

根据对数似然函数，利用Newton-Raphson 迭代法可求得ZIP模型中各参数的估计值[20]。

ZIP模型理论上可对零观测值分类，但究其来源，对于观测值为零的爆管记录，并不能准确判断其具体过程，更不能判断是何种原因造成的。

1.4 零膨胀泊松模型的Score检验

采用Score检验方法检验爆管计数资料是否存在零膨胀现象。当Gi,t=0 时，ZIP 模型就等价于泊松(Poisson)模型，因此，判断爆管数据集是否适合零膨胀模型，等价于检验Gi,t=0 成立还是Gi,t＞0成立。

当Gi,t=0时，S统计量服从自由度为1的卡方分布，即

当计算得到的S 统计量大于3.84 时，即可在95%的显著性水平下拒绝原假设，认为该数据样本存在零膨胀现象。

1.5 爆管次数预测

基于ZIP模型参数估计得到期望λi,t与相关协变量的公式，可知区域内t时间i号管道爆管发生概率，则t时间管道爆管总次数为

其中：k=1，2，…，m；m为t时间i号管道爆管的最高次数。

2 实例分析

基于ZIP模型的爆管预测的总体模型称为零膨胀爆管预测模型，在实际建模与模型应用过程中，需要研究区域一段时间内的管材、管径、管龄、温度、降雨量、爆管历史和管长等影响因素数据，用以统计分析。通过参数估计可以分析出各影响因素与发生爆管的相关性，并预测研究区域某时间内爆管总次数。

2.1 爆管影响因素

爆管影响因素包括：a)静态变量：管径、管长、管材；b)动态变量：管龄、温度影响指数、降雨量、交通荷载；c)动静态变量：爆管历史总次数、阴极保护。

1)管径为模型内生变量，直接考虑进爆管预测中，选取管径为100～300 mm 的主干管，用z1表示；

2)管长为样本中该主干管的长度，用z2表示；

3)管材为灰口铸铁管，对于不同管道均为同一材质，用z3表示，单一管材预测，z3可取值为0；

4)管龄用p1表示，p1≥5 a；

5)温度影响指数为1 a 内日平均温度低于5 ℃的时间和高于30 ℃的时间之和，用p2表示：若预测年份的温度影响指数未知，则采用其修正值p2,t表示：

①在当年的12月份预测次年的爆管次数时，采用次年前3年的温度影响指数计算平均值，得到温度影响指数的修正值p2,t；

②在当年的1～11月份预测当年的爆管次数，按式(13)计算时间段内数据平均值之和，得到温度影响指数的修正值p2,t

式中，为当年内已知月份的日平均温度低于5 ℃与高于30 ℃的时间之和，d；和p′2,t-3分别为当年前1年、前2年、前3年未知月份相应的日平均温度低于5 ℃与高于30 ℃的时间之和，d；

6)年降雨总量，用p3表示，表征土壤含水率对爆管的影响，预测年份的降雨量未知时，处理方式同温度影响指数，采用降雨量修正值p3,t；

7)城市地下供水管道所受的交通荷载通过土体传递，用p4表示，若城市地下供水管线所受交通荷载相同或相近，则可取为0；

8)爆管历史总次数：某根管道i自建设完工后至所预测的第t年之前发生过的爆管次数总和，用q1表示；

9) 阴极保护：考虑是否有阴极保护，用q2表示。

对爆管影响因素进行变量描述性统计，得到样本数据各变量的均值、标准差、最小值与最大值，根据式(4)进行过离散检验，然后建立ZIP 模型，根据对数似然函数，利用Newton-Raphson 迭代法式(10)可求得ZIP 模型中各参数的估计值，再根据以上估计值采用S统计量进行计数资料零膨胀复验。

将以上影响因素参数代入式(6)得预测期内单根灰口铸铁管的爆管期望值计算建模如下：

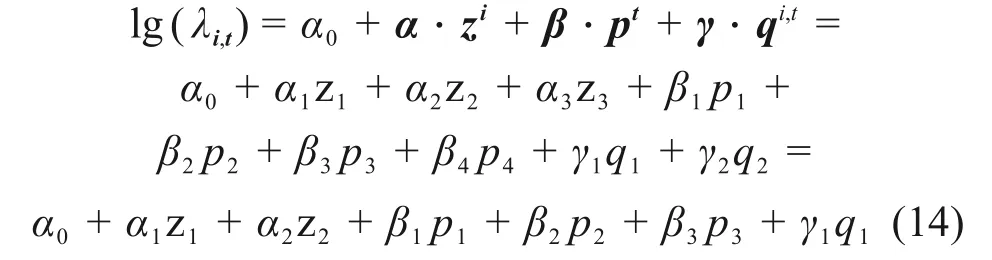
最终根据式(12)可得到最终某区域某时间段内爆管总数。

2.2 数据选取及整理

考虑到某省M 市研究区域内PE 管、PPR 管中大部分为管径小于100 mm 的进户管和庭院配水管，爆管一般发生在各小区内，建设年限在10 a之内，虽然钢管爆管较多，但基本为新建钢管，还处于爆管“浴缸曲线”的开始阶段，而球墨铸铁管、钢塑、水泥等其他管材管道所占比例较小且基本没有爆管记录，对于灰口铸铁管，直径大于300 mm的管道没有爆管记录，因此，选定管材为灰口铸铁管且管径在100～300 mm之间的主干管建立爆管预测模型。研究区域内灰口铸铁管建设年限在1969—2000年，导出系统中管网GIS 图中100～300 mm 管道信息，共包括1 789 根管道，管道总长90.07 km。因近几年管线改造等原因，为保证数据完整全面，选取2006—2013年总计8 a的爆管记录作为样本，建立爆管预测模型。所采用天气数据来源于国家气象信息中心收集的数据。

不同管径的管道爆管次数统计如表1所示。

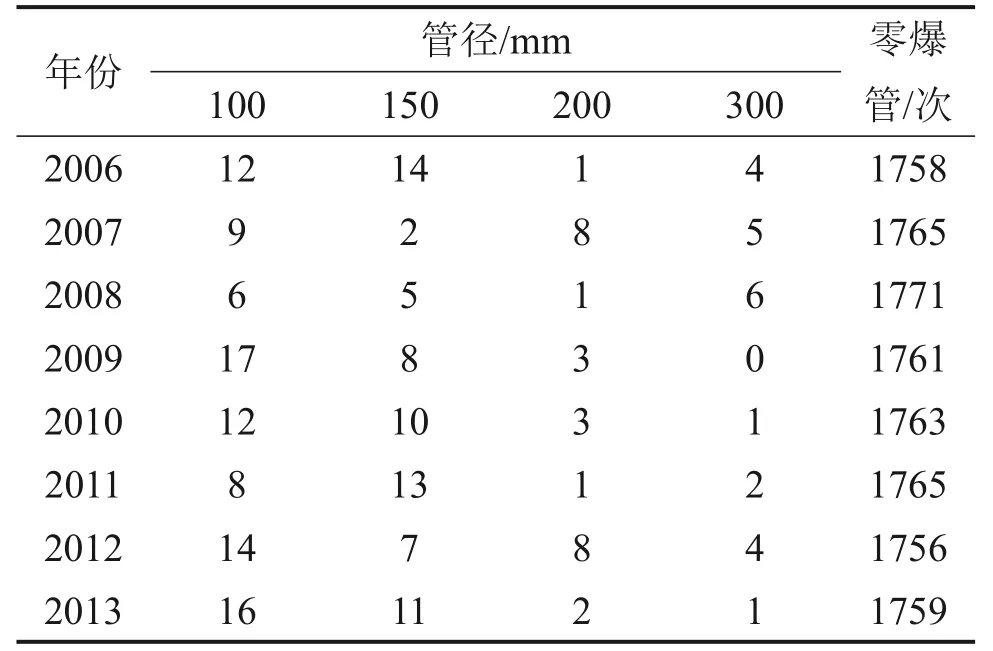
表1 灰口铸铁管不同管径爆管次数Table 1 Number of pipe breaks with different diameters

通过爆管因素分析可知，低温和高温对爆管均有影响。2006—2014年的温度影响指数如图1所示。由图1 可知：温度影响指数最高为2011年的43 d，最低为2007年13 d，年际变化大。

图1 研究区域温度影响指数Fig.1 Temperature influence coefficient of study area

采用该地区年降雨总量表示土壤含水率对爆管的影响，研究区域属季风气候区域，降雨量比较充沛，且年际变化很大，2006—2014年总降雨量变化如图2所示。由图2可知：降雨总量最高为2007年的1 039 mm，最低为2006年的593 mm。

图2 研究区域年降雨总量Fig.2 Annual rainfall of study area

本研究未考虑交通荷载、阴极保护、接口形式等对爆管也有影响的模型变量，采用管道i在t之前已发生历史爆管总次数表示爆管历史对爆管的影响。将所考虑的影响因素预处理后，开展下一步分析。

2.3 数据集检验及参数估计

为验证上述爆管数据存在零膨胀现象，利用SAS中的PROC Means过程对各协变量进行描述性统计分析，得到样本数据各变量的均值、标准差、最小值与最大值，结果如表2所示。

从表2可以看出：年降雨总量、管径和管长的波动相对较大。爆管数均值为0.014 96，方差为0.135 52，根据式(4)计算得到O统计量为19.29大于95%显著性水平下的O统计量1.96(P＜0.05)，即在95%的显著性水平下拒绝原假设，认为该数据样本存在过离散现象。

表2 协变量描述性统计结果Table 2 Descriptive statistical results

利用统计软件SAS中的PROC NLMIXED过程进行参数估计，该过程主要用于模型的非线性拟合。为了直观显示各因素变化对管道爆管概率的影响程度，建模之前并未对变量进行标准化处理。参数估计结果如表3所示。由表3可以看出：

表3 爆管期望的ZIP模型参数估计结果Table 3 Parameter estimation results of expected values in ZIP model

1) 爆管期望与管径呈负相关，即管径越小，爆管发生的概率越大，与理论研究和其他研究结果一致，且P＜0.000 1，说明该参数估计高度显著。

2) 爆管期望与管龄呈正相关，即管龄越大，爆管发生的概率越大，与理论研究和其他研究结果一致，且P＜0.01，说明该参数估计高度显著。

3) 爆管期望和温度指数、降雨量呈负相关，即温度指数越小，降雨量越少，爆管发生的概率越大，但是P＞0.1，说明该参数估计不显著，原因可能是研究区域管道埋深较深，对环境因素不敏感，且研究区域处于亚热带，气候适宜，极端天气少。

4)爆管期望与爆管历史呈正相关，即历史发生过的爆管次数越多，其爆管发生概率越大，与理论研究一致，且P＜0.01，说明该参数估计高度显著。

5) 爆管期望与管长呈正相关，即管长越大，其发生爆管的概率越大，可能原因是管道越长，不均匀沉降的影响也越大，且P＜0.000 1，说明该参数估计高度显著。

根据模型估计参数算得研究期限内的爆管期望，由式(11)求得S 统计量为6 903.22，大于95%显著性水平下的S 统计量3.84(P＜0.05)，即在95%的显著性水平下拒绝原假设，因此可以认为爆管数据集存在零膨胀现象，适合采用零膨胀爆管预测模型。

2.4 预测结果及精度分析

设定爆管发生的判别概率(结构零的比例Gi,t)，应用爆管预测模型对2006—2013年的年爆管总数进行模拟预测，结果如图3所示。

由图3可以看出：研究期内各年预测爆管总数与实际爆管总数比较接近，爆管总数平均预测精度达到86.98%，说明零膨胀爆管预测模型在预测年爆管总数上准确率较高。

由于爆管记录年限的限制，仅选取2014年的数据作为检验样本，检验零膨胀爆管预测效果，结果如表4所示。

表4 爆管预测模型预测检验Table 4 Prediction results test of prediction model

定义模型的预测精度为

定义模型预测的吻合程度为

图3年预测爆管总数与实际爆管总数对比Fig.3 Comparison of predicted and actual pipe failure

根据表4，由式(15)计算得模型的预测精度η=79.41%，说明模型预测爆管总数的精度较高。且由式(16)计算得模型预测的吻合程度γ=14.81%，说明定位到具体管道时模型的预测结果欠佳。究其原因，可能是用于检验样本量过小。零膨胀爆管预测模型是根据平均爆管期望计算爆管率，实际情况下管道爆管却是随机事件，当检验样本足够大时，观测值就会趋于它们的平均值。

3 模拟预测效果比较

ZIP 模型是二项Logistic 分布与Poisson 分布组成的混合分布，由此分别采用爆管预测Logistic广义线性模型及爆管预测Poisson 回归模型与零膨胀爆管预测模型比较。

3.1 Logistic模型拟合结果

协变量选取与ZIP 模型相同，Logistic 模型如下：

其中：p为爆管发生的概率；a为常数项；bi为回归系数；xi为自变量。

利用SAS 对模型参数进行拟合，爆管预测Logistic模型参数拟合结果具体如表5所示。

表5 Logistic模型参数估计结果Table 5 Parameter estimation results of Logistic model

从表5可以看出，管径越大，爆管发生概率也越大，与描述性统计研究及零膨胀爆管预测模型得到的结果相反，但是P＜0.000 1，参数估计值高度显著；管龄越大，爆管发生的概率越大，与理论研究和零膨胀爆管预测模型结果一致，且P＞0.1，说明该参数估计不显著；温度指数越大，降雨量越大，爆管发生的概率越大，与理论研究一致，但与零膨胀爆管预测模型结果相反，P＞0.1，说明该参数估计不显著；历史发生过的爆管次数越多，其爆管发生概率越小，与理论研究和零膨胀爆管预测模型结果相反，且P=0.000 1，说明该参数估计高度显著；管长越大，其发生爆管的概率越小，与零膨胀爆管预测模型结果相反，且P＜0.000 1，说明该参数估计高度显著。

3.2 Poisson模型拟合结果

同样利用SAS 对模型参数进行拟合，爆管预测Poisson模型参数拟合结果具体如表6所示。

从表6 可以看出：爆管预测Poisson 模型参数拟合结果的正负号与零膨胀爆管预测模型一致，说明对于研究区域内的爆管数据，爆管预测Poisson 模型和零膨胀爆管预测模型得到的各影响因素对爆管的影响效应是一致的，除管龄外，其他影响因素的显著性也与零膨胀爆管预测模型一致。而对于管龄，爆管预测Poisson 模型得到的P＞0.1，说明参数估计不显著，但是零膨胀爆管预测模型的参数估计是显著的。

表6 Poisson模型参数估计结果Table 6 Parameter estimation results of Poisson model

3.3 模拟预测效果比较

设定相同的爆管发生判别概率，研究期内3种模型的爆管模拟预测效果与实际观测值的对比如图4所示。

由图4 可以得出，在研究期内，Poisson 模型、Logistic模型和ZIP模型的预测精度分别为65.44%，70.79% 和86.98%，ZIP 模型预测效果最优，Poisson模型过高地预测了年爆管总数，而Logistic模型过低地预测了年爆管总数。

图4 各模型爆管预测结果与实际对比Fig.4 Comparison of predicted and actual pipe failure in different models

4 结论

1)引入ZIP模型，使模型更吻合实际情况。与Logistic模型和泊松(Poisson)模型的预测结果相比，基于ZIP模型的爆管模拟预测模型效果最优。

2)根据ZIP模型参数估计结果，爆管期望与管径、温度影响指数以及降雨量呈负相关，且与管径因素高度相关，与管龄、爆管历史以及管长呈高度正相关。

3)将ZIP爆管预测模型预测爆管结果与统计数据对比分析可知，对爆管事件发生总次数的识别精度达86.98%。利用2014年数据作为检验样本对单根管道爆管预测模型进行检验，年爆管总次数的拟合精度达79.41%，但是针对单根管道本模型预测的吻合度为14.81%，说明定位到具体管道时模型的预测结果相对误差较大。