“双减”背景下小学数学错题评讲优化策略

【摘要】本文结合“双减”政策探讨小学数学错题评讲优化的现实意义，通过分析教师错题评讲中的常见问题、小学生数学作业和试卷中的错题类型及其错误的根源，明晰错题的教学资源价值，结合案例阐述错题评讲优化三大策略，即引导学生在自主反思中记住错题及其出错原因、用“错题笔记”强化纠错记忆、在重构典型错题和“借题发挥”中发展逻辑思维能力。

【关键词】“双减” 错题评讲优化 策略

【中图分类号】G62 【文献标识码】A

【文章编号】0450-9889（2022）01-0015-03

随着中共中央办公厅、国务院办公厅《关于进一步减轻義务教育阶段学生作业负担和校外培训负担的意见》的出台，学生过重作业负担和校外培训负担、家庭教育支出和家长相应精力负担“1年内有效减轻、3年内成效显著”这两个带有时间节点的“双减”工作目标，迅速引发了全网热议。自2021年秋季学期起，“双减”政策开始在全国各地中小学校逐渐推行。对学校来说，“双减”工作的重点是积极、有序、有效地开展好校内课后服务工作，引导各学科教师通过在校内适当安排巩固练习，“确保小学一、二年级不布置家庭书面作业”“小学三至六年级书面作业平均完成时间不超过60分钟”，同时加强对学生作业完成的指导;对各学科组及每一名教师来说，工作重点是通过强化学科教研，进一步提高本学科课堂教学质量、优化本学科作业设计和错题评讲过程。

在此背景下，笔者通过深入研究学生作业和试卷中的错题，基于学生出错原因优化错题评讲策略，在发展学生数学思维的同时，帮助学生构建相关知识体系，取得了较好的实践效果。

一、小学数学教师错题评讲中的常见问题

笔者在观察中发现，小学数学教师在错题评讲中的常见问题是就题论题、流水线讲题并公布正确答案，导致学生对错题缺乏积极、有效的管理，只会跟着老师一题接一题地订正错误。其背后根源，其实是教师没能发现错题的教学资源价值，未对学生作业和试卷中出现的错题进行深入研究，从错题中挖掘隐含的“教情”与“学情”信息，包括错题的知识背景、题目类型、难易程度以及学生的出错原因、出错频率等。教师习惯于“出错→纠错”式循环评讲，学生“奔波在”课堂被动纠错的“学习”过程，并因此错失了对错题的深入认识和有效管理，错失了以自身和同学的错题为学习资源进行深度思考、合作探究改正错误、提高认识的良机。

错题之所以是重要的教学资源，是因为错题的背后往往隐含着学生在学习和答题过程中所产生的各种认知漏洞。教师在错题评讲过程中帮助学生及时修补漏洞，有利于学生接下来的数学学习。数学学科是一门逻辑性极强的学科，知识与技能学习环环相扣，其中任何一个节点的知识与技能缺失，都会影响学生接下来的数学学习。

二、小学生数学作业或试卷中的错题类型及错误归因

学生在完成作业和考试答题的过程中，时常会出现各种各样的错误。将错题进行分类整理，有利于教师优化错题评讲策略，让错题成为真正的教学资源。笔者结合多年教学实践研究，将小学生在数学作业和考试答题中常见的错误划分为知识性错误、逻辑性错误、策略性错误、心理性错误四种类型，其中：知识性错误是学生最容易出现的错误，错误的根源是学生未能正确理解数学基本概念，没有真正掌握数学公式和定理的准确用法;逻辑性错误主要表现为论证错误、不等价转换、“以点代面”等，错误的根源是学生对题目信息的理解出现了偏差或概念认知模糊，由此导致解题思路偏差;策略性错误的根源是学生对知识点的掌握不够准确，未能选择恰当的解题方法，导致在解题过程中设定了错误的数学模型;心理性错误主要出现在考试答题的过程中，原因是小学生的心理承受能力较弱，考试时紧张，导致在考场中瞬间遗忘知识点、出现记忆偏差等。

分析错题类型及错误产生的根源，有利于教师在错题评讲过程中准确把握学情、定位错题评讲的着力点，优化错题评讲策略，引导学生及时发现自身存在的真正问题，并以此为基础优化学习策略，“对症下药”，切实提高学习效率。

三、小学数学错题评讲优化策略

美国学者爱德加·戴尔的学习金字塔理论认为：采用不同的学习方式，学习者在两周以后还能记住内容（平均学习保持率）的多少是呈金字塔形排布的。采用塔尖的第一种学习方式“听讲”，两周后仅能记住学习内容的5%;采用第二种学习方式“阅读”，两周后可以记住学习内容的10%;采用第三种学习方式“声音、图片”，两周后可以记住学习内容的20%;采用第四种学习方式“示范”，两周后可以记住学习内容的30%;采用第五种学习方式“小组讨论”，两周后可以记住学习内容的50%;采用第六种学习方式“做中学”或“实际演练”，两周后可以记住学习内容的75%;采用最后一种学习方式“教别人”或者“马上应用”，两周后可以记住学习内容的90%。他发现，学习效果在30%以下的几种学习方式，都是个人学习或被动学习;而学习效果在50%以上的，都是团队学习、主动学习或参与式学习。笔者基于学习金字塔理论，提炼了错题评讲优化的三大策略。

（一）引导学生在自主反思中记住错题和出错原因

过去，学生习惯于消极等待教师在课堂中为其讲解、订正错题，以“听讲”为主要学习方式。为了提高学生的学习效率，笔者以为，错题评讲课必须更多地发挥学生的主动性，引导学生自主反思出错原因并修正自己的解题思路，通过“做中学”，最大限度地记住错题和出错原因。

如，笔者在批改数学一年级下册《100以内的加法和减法（一）》单元测试题时，发现了一道学生出错率较高的填空题。

全班40名学生做两道题，有11名学生只做对第一道题，9名学生只做对第二道题，其他学生两道题都做对了。请问：①两道题都做对的有（  ）名学生;②只做对一道题的有（  ）名学生;③两道题都做错的有（  ）名学生。

关于该题第①小题，大部分学生填写的答案是“20”，部分学生填写的答案是“9”，个别填写了其他答案;第②小题，大部分学生填写的答案是“11”，个别填写其他;第③小题，部分学生填写的答案是“9”和“29”，少部分学生正确填写了“0”。

这是一道比较简单的综合应用题，但全班学生出错率如此高，根源在于学生审题不够仔细，混淆了题目中的相似概念，导致解题思路偏差。在讲解此题时，笔者先让学生认真读题3遍，再说出自己对题目的理解，特别是对“两道题”和“第二道题”、“一道题”和“第一道题”这两组概念的理解，促使学生主动反思出错原因，发现审题不仔细的根源在于误将题枝中的“一道题”等同于题干中的“第一道题”，误将题枝中的“两道题”等同于题干中的“第二道题”，并因为题干中未出现“做错”的人数而想当然地把“做错”当成了“做对”，导致在回答第②小题时未将“只做对第二道题的人数9”计入“只做对一道题的人数”当中，且第③小题的答案因为未做“做对”与“做错”的分类辨析而出错。

慢速读题、自主反思，让学生对题目中的两组概念有了更清晰的认知，同时也意识到仔细审题、有效提取数学信息的重要性。随后，笔者组织学生进行了类似题型的干扰训练，直到情况彻底改观。

（二）引导学生用“错题笔记”强化纠错记忆

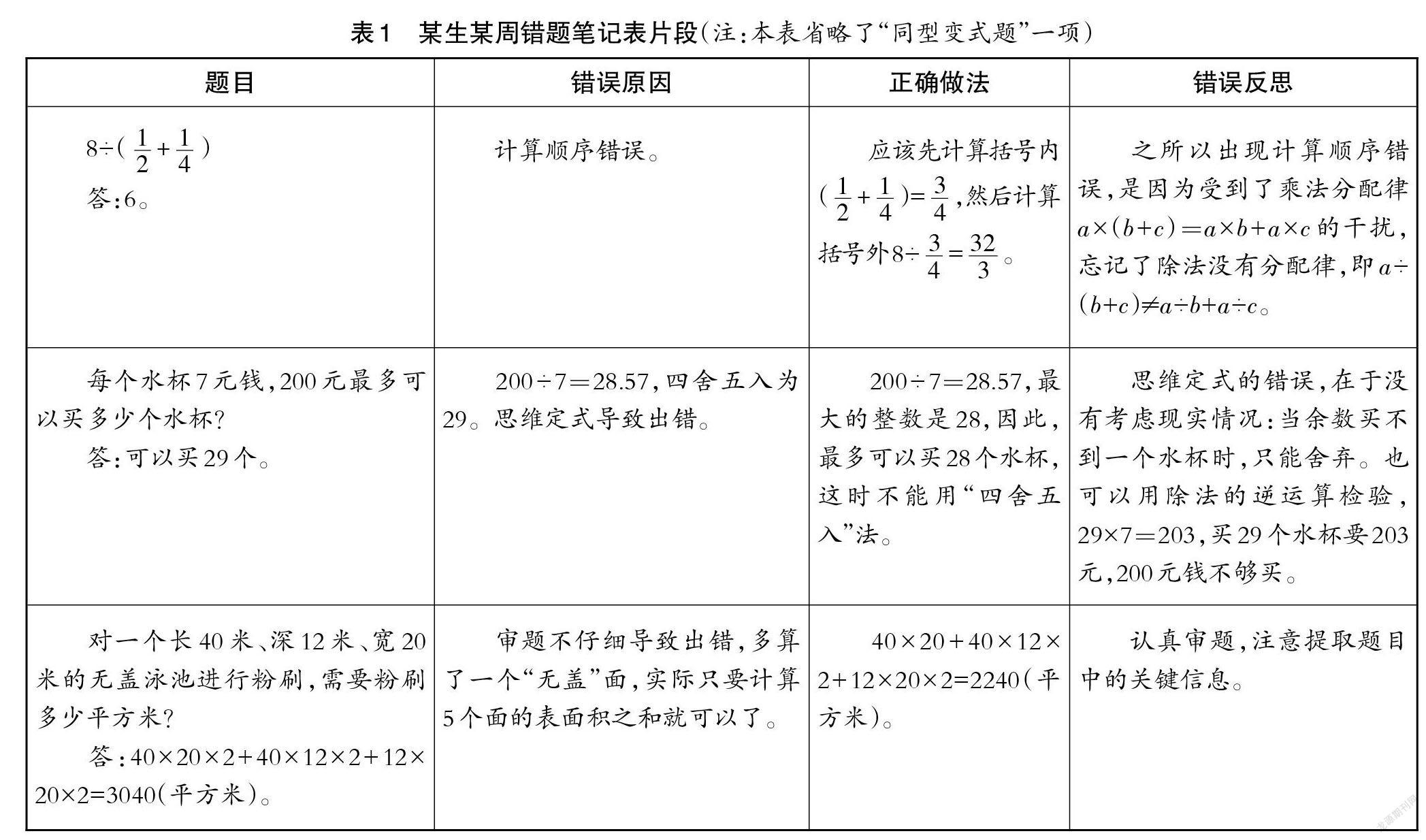
小学数学错题评讲的目的是帮助学生纠正学习和答题过程中出现的各类认知错误，弥补遗漏知识、巩固已学知识、拓宽解题思路、训练数学思维。以上教学目的决定了教师在评讲错题时，不应局限于“完成作业”式的评讲，而应注重引导学生认真记录和整理出错最多的题型，总结错误发生的原因，养成错题反思的习惯，为后续学习和复习做好铺垫，避免出现“被动纠错—机械重复—再次出错”的低效学习状态。为此，笔者给学生设计了一种“错题笔记表”，表头设“题目”“错误原因”“正确做法”“错误反思”及“同型变式题”五项（见表1示例），让学生将每周的错题和自己的反思过程逐一记录下来，促进学生对知识的理解和运用，帮助学生形成自觉反思的习惯，达到巩固知识、理解知识和运用知识的目的。

（三）引导学生在重构典型错题和“借题发挥”中发展逻辑思维能力

所谓典型错题，指的是学生普遍容易出错的类型题。对典型错题进行多层次的剖析、讲解，从中提炼重点知识和学习方法，处理好新旧知识点的对接，不仅有利于学生构建小学数学知识体系，而且有利于学生掌握正确的解题思路和方法，提高逻辑思维能力和解决问题能力。

笔者在进行错题评讲时，时常选取具有较大灵活性和剖析余地的典型错题，先对其逐步拆解，再“借题发挥”，引导学生由浅入深地理解其中的知识点，学会多角度分析问题，以错题为原点适当延伸，进而构建相关数学模型，提高解题能力。

例如，笔者曾经给学生布置了一道分数应用题：甲、乙、丙、丁四人合买一台音响，甲支付的钱数是其他三人所付总钱数的[16]，乙支付的钱数是其他三人所付总钱数的[14]，丙支付的钱数是其他三人所付总钱数的[13]，现已知丁支付的钱数为570元，请问这台音响的总价是多少元？

这道题，全班学生的解题正确率极低，且出错的方式各不相同。导致出错的根源是，学生无法理顺四人出资之间的数量对应关系。从题目上看，四人所付的金额比例分别是“其他三人所付总钱数”的[16]、[13]、[14]，但学生很难理解“其他三人”不是同一个数暨并非“相同的三个人”，也就是说，[16]、[13]、[14]不是同一个钱数的[16]、[13]、[14]。为了帮助学生厘清题目中的数量对应关系，笔者在评讲过程中采取了拆解题目、变式对比、同型拓展的方式，引导学生逐步掌握分析问题、解决问题的思路和方法。

第一步，笔者将题目中的数量关系拆解为相对简单的一一对应关系，帮助学生理解比例与数量之间的对应关系。经过拆解（过程略）后，可以得出“甲支付的钱数是乙的[57]”。之后笔者要求学生计算下列数量关系：①若以甲的钱数为单位1，那么乙的钱数是甲的（  ）;②若以甲、乙二人的钱数和为单位1，那么甲的钱数占两个人总钱数和的（  ）;③若以甲、乙二人的钱数差为单位1，那么甲的钱数是两人钱数差的（  ）。通过拆解、变换，学生终于厘清了题目中的数量对应关系。

第二步，笔者将原题进行变形，让学生对比二者的不同：甲、乙、丙、丁四人合买一台音响，甲支付的钱数是这台音响总价的[17]，乙支付的钱数是这台音响总价的[15]，丙支付的钱数是这台音响总价的[14]，现已知丁支付了570元，请问这台音响的总金额是多少元？学生在解答这道变式练习的过程中，发现了两道题目中数量关系的不同，对原题题意有了更清晰的理解，进而理顺了原题中甲、乙、丙、丁四人各自出资的正确比例，找到了正确的解题思路。

第三步，为巩固学生所学，笔者开始“借题发挥”，设计了下面的同类型题目：三年级有4个班级，一班人数是二班、三班、四班人数总和的[12]，二班人数是一班、三班、四班人数总和的[14]，三班人数是一班、二班、四班人数总和的[15]，已知四班有55人，三年级共有多少人？

用拆解、变形和拓展的方式重构典型错题，可以帮助学生更好地发现、理解和巩固题中涉及的知识点，有助于学生发现错题的“错情”、找到“错源”，理顺解题思路，发展逻辑思维。

在“双减”背景下，教师通过优化错题评讲策略，提高错题评讲质量，不仅可以帮助学生弥补知识缺陷、加深对知识点的理解和記忆、提高问题分析和解题能力，而且可以培养学生良好的数学学习习惯，促进其数学思维的发展。

作者简介：曹文锋（1977— ），福建上杭人，小学一级教师，研究方向为小学数学教学。

（责编 白聪敏）