基于压缩感知的VLC非线性均衡器研究

刘希　苗圃　田大明

文章编号：10069798（2022）02000707;DOI：10.13306/j.10069798.2022.02.002

摘要：为解决Volterra级数的非线性均衡器（volterraseriesnonlinearpost-distortionequalizer，VS-NPE）内核数量大、计算困难等问题，本研究采用压缩感知重构算法中的正交匹配追踪算法（orthogonalmatchingpursuit，OMP）和改进的近似消息传递算法（approximatemessagepassing，AMP）计算VS-NPE内核参数。改进的AMP算法应用时，需对VS-NPE测量矩阵归一化处理，然后将AMP算法迭代过程引入阻尼因子和稳固阈值函数，进而提高模型构建精度。仿真结果表明，在训练样本长度较小时，OMP算法和改进的AMP算法仍拥有较高的重构精度，且OMP算法计算的模型内核数量减少65%，有效降低模型复杂度。另外，基于上述两个算法的VS-NPE在归一化功率谱和误码率（biterrorratio，BER）性能上展现了良好的失真补偿性，证明了所提方案的有效性和可行性。该研究有助于构建强健的VS-NPE模型，显著缓解可见光通信系统信道非线性失真。

关键词：可见光通信;非线性均衡器;压缩感知;正交匹配追踪

中图分类号：TN911.22;TN92;TP391.9文献标识码：A

可见光通信（visiblelightcommunication，VLC）是一种新型的信息传输方式，缓解了传统无线通信系统频谱资源紧缺的问题。但VLC系统具有严重的非线性失真，其最关键的因素是LED非线性特性。近年来，有学者提出预失真补偿技术和后失真补偿技术，其中基于后失真补偿技术的非线性均衡器因其优势明显而被广泛应用[13]。均衡器是根据VLC强度调制直接检测（intensitymodulationdirectdetection，IM/DD）的逆特性构造非线性模型，将其放置在接收端，对IM/DD信道进行非线性补偿。沃尔特拉级数（volterraseries，VS）在建模动态非线性系统方面的优势，常被用作均衡器行为模型的基本函数[25]。基于VS的非线性后失真均衡器（VS-nonlinearpost-distortionequalizer，VS-NPE）建模的关键是其内核参数的提取，而VSNPE内核个数随着非线性阶数和记忆深度呈指数增长，增加了内核参数计算难度。因此，降低计算复杂度，提高计算精度成为VS内核参数提取的关键问题。常用的内核计算方法包括最小二乘（leastsquares，LS）[1]、递归最小二乘（recursiveleastsquares，RLS）[2]、卡尔曼（Kalman）滤波[4]和压缩感知（compressedsensing，CS）[67]等，其中LS虽结构简单，但在进行参数更新时需反复进行耗时较多的矩阵求逆运算。相比之下，RLS收敛性较好，但其复杂度较高[2];Kalman滤波具有良好的稳定性，但是算法中的噪声和测量噪声对参数估计影响较大[4]。CS是一种有效的稀疏重构方案[67]，可实现在信号采样的同时完成压缩，并利用较少的采样值对信号进行重建，实现了低复杂度的压缩编码。重构算法是CS的核心，常见的重构算法有正交匹配追踪（orthogonalmatchingpursuit，OMP）[8]、近似消息传递（approximatemessagepassing，AMP）[9]和基本追踪（basicpursuit，BP）[6]等。CS的可行性要求重构信号在变换域中是稀疏的或本身是稀疏的，且测量矩阵应满足有限等距性质（restrictedisometryproperty，RIP）的条件。VS的内核参数满足稀疏性且测量矩阵满足RIP条件。基于此，本研究利用OMP和AMP算法计算VS-NPE内核参数，仿真分析其内核计算能力，评估VS-NPE模型[1011]对VLC系统失真补偿性能，为缓解VLC系统非线性失真提供了一种基于压缩感知的VS-NPE方案。该研究具有一定的可行性和有效性。

1系统模型

1.1OFDM调制

正交频分复用（orthogonalfrequencydivisionmultiplexing，OFDM）调制技术由于其传输速率高且抗码间干扰强的优势，多被用于VLC系统中。该系统使用IM/DD方法传输单极性实信号，传统的OFDM需限制输入信号的频谱，使其满足Hermitian共轭对称，进而输出单极性实信号。目前实现上述目標的方法有直流偏置正交频分复用（DC-biasedopticalorthogonalfrequencydivisionmultiplexing，DCO-OFDM）调制技术[12]和非对称限幅（asymmetricallyclippedopticalorthogonalfrequencydivisionmultiplexing，ACO-OFDM）调制技术，本研究采用DCO-OFDM调制技术对VLC系统进行建模。

1.2IM/DD信道

IM/DD是收发两端采用LED和光电二极管（photodiode，PD）分别完成电光转换、光电转换的通信系统。基于IM/DD信道的VLC系统如图1所示。图1中，发送端将信号源映射到子载波，双极性信号通过添加直流偏置而转换为单极信号，并驱动LED调制得到光信号，在自由空间传播链接之后，光信号由PD捕获并转换为电信号。因此，IM/DD信道建模应同时考虑LED、光信道和PD。

LED常表现出非线性记忆效应[1314]，因此，本研究借助Wiener模型对LED建模，该模型包括线性时不变（lineartimeinvariant，LTI）模块和非线性（nonlinear，NL）模块[15]。LTI模块可表示为

其中，n为函数变量;fc为截止频率，fc=20MHz。NL模块建模为

实际的LED具有单向导电性和非线性。因此，建模后的LED应设置最小开启电流Imin=0.1A，最大前向电流Imax=1A和直流偏置IDC=0.4A，使LED工作在有效工作区。

本研究采用IEEE802.11协议的室内可见光多径信道模型，其信道脉冲响应（channelimpulseresponse，CIR）可表示为

其中，Nr是在探测器处接收到的射线数量;Pn是第n射线的光功率;δt是狄克拉函数;τn是第n射线的传播时间。将PD视为狄克拉响应hPDn=RPDδn，设RPD=1为响应度。

信道噪声建模是均值为零且方差为σ2e的加性高斯白噪声（additivewhitegaussiannoise，AWGN），则输出zn可表示为

其中，f（n）是NL模块输出;xn表示DCO-OFDM调制信号;表示卷积运算;hNr是信道脉冲响应;en表示信道噪声。由式（4）可得，zn涉及的LED非线性和色散效应将影响随后的信号解调。因此，在接收端设计信号处理模块对信号zn进行均衡，以补偿LED非线性失真及信道损失。

1.3后失真均衡器行为模型

VS模型是可用于非线性系统的通用模型，可以逼近任意非线性函数。本研究采用VS建立后失真均衡器模型，对应的全内核VS-NPE输出[4]可表示为

其中，K是非线性阶数;Hk[zn]表示激励;zn表示VS-NPE的输入;D是记忆深度;hkc1，…，ck是VS内核;Ωkn=∏ki=1zn-ci是对应的回归量;en是测量噪声。由于VS的输出与内核系数是线性关系，可将式（5）重写为矩阵形式，即

其中，x是输出信号的连续采样向量;Z是VS测量矩阵;h是VS模型内核列向量;e是测量噪声向量。由式（6）可知，构建后失真均衡器模型的关键是内核向量h的估计。

本研究训练VS-NPE模型时，将IM/DD信道模型中的xn和zn作为训练样本，利用一些信号处理算法获得VS-NPE的内核系数，进而得到估计值n，以min‖xn-n‖2=min‖en‖2为优化目标来评估参数计算方法的优劣。

2基于压缩感知的VS-NPE参数计算

2.1OMP算法

压缩感知是一种稀疏信号重构方法，即从y∈RN测量结果中恢复稀疏信号h∈RM。其测量模型为

式中，A∈RN×M表示传感矩阵;n是噪声。压缩感知理论的关键是通过解决优化问题实现重构，重构信号为

其中，是重构信号;‖h‖1是h的l1范数;ε是信号重构的上限误差。

OMP是CS的重构算法之一，可用于解决式（8）的优化问题。OMP算法在匹配追踪算法的原子选择策略基础上正交化所有选定的原子，然后使用LS更新所选原子的线性组合系数，每次迭代都会更新所选原子集[16]。该算法从查找矩阵A和y最相关的行开始，反复查找信号的残差值。与残差rt的相关性由下式进行选择，即

其中，pt是索引项;i是原子下标;S是所选系数集;（·）H是对矩阵做共轭转置;A为传感矩阵;rt是迭代t次的残差值。将所选索引合并到所选系数S=S∪pt的集合中，再利用LS计算重构信号，即

其中，y是测量值。每次迭代的残差重新计算作为原子选择的新标准。

2.2AMP算法

AMP[9]算法是解决式（8）优化问题的一种有效方法。该算法从0=0，0=y迭代开始，在迭代t次时，AMP算法可表示为

其中，y是测量值;A是传感矩阵;t∈RM是h迭代t次时的当前估计;rt-1是迭代t-1次时的残差;‖t‖0是当前估计t中的非零个数;N表示矩阵A的行数;η·;·是软阈值函数;AT表示矩阵A的转置;θ是阈值参数。η·;·的表达式为

其中，signx是符号函数;α=1.005是通过迭代固定的调整常数;σ是经验度量;N是残差向量的维度。

2.3稳固阈值AMP算法

AMP算法有效的前提是测量矩阵应满足独立同分布（independentlyidenticallydistribution，IID）[17]，VS-NPE测量矩阵未能达到IID标准。本研究将归一化处理测量矩阵，使其格式更为标准便于后续数据处理。提出一种稳固阈值的AMP（stabilitythreshold-AMP，ST-AMP）算法用于VS-NPE内核计算，ST-AMP算法核心思想是在AMP算法基础上引入阻尼思想，并修改软阈值函数为稳固閾值函数，结合LS算法完成内核计算。根据训练样本的输入信号和VS-NPE模型信息，生成VS测量矩阵Z=z1…zN∈RN×M，以Z的列特征计算归一化因子Ψ=diag‖z1‖2，…，‖zN‖2∈RM×M[18]，利用Ψ将等式（6）重写为

其中，ZΨ=ZΨ-1表示归一化测量矩阵;hΨ=Ψh表示VS-NPE的归一化内核;e表示测量噪声。通过归一化处理Z，使新矩阵ZΨ更加方便进行数据处理。

在AMP算法迭代过程引入阻尼技术[19]来提升算法收敛性，并修改存在恒定误差的软阈值函数为稳固阈值函数，最终得到ST-AMP算法迭代过程，即

其中，rt是迭代t次时的残差;β1，β2∈0，1是阻尼因子，设置β1=β2=0.008;htΨ是重构信号;bt与式（11）中的含义一致;γ·;·是稳固阈值函数，可弥补软阈值函数的恒定误差[20];θ与式（12）中的含义一致;γ·;·定义为

其中，参数b是正实数，设置b=2。

当hΨ的估计满足收敛要求时，提取支持集h=Ψ-1hΨ。其中h的稀疏支持集是h的大系数分量的下标集Ni=i：（h）i>μ，μ是系数阈值。提取Ni后，用LS算法计算基于Ni的uΨ为

其中，A为传感矩阵;uΨ=hNi。根据Ni信息对h进行重构，得到VS-NPE参数内核。

3仿真分析

根据上述理论，搭建基于IM/DD信道的VLC系统，通过迭代收敛性、归一化均方误差（normalizedmeansquareerrer，NMSE）ENMS性能、内核数量和线性化能力等方面对比OMP算法和ST-AMP算法性能。训练所需的模拟环境采用文献[21]室内空房间的VLC信道模型，训练样本选取带宽125MHz，循环前缀长32的DCO-OFDM信号，而验证数据的设置也区别于训练样本。

3.1模型结构

由于记忆深度D和非线性阶数K的确定直接影响了VS-NPE模型的结构和性能，对比两个算法性能之前，需提前确定参数（D，K）。本实验仿照粒子群的寻优思想确定模型参数（D，K），以ENMS作为寻优目标，D分别选取2～5，K分别选取1～5，共组成20组（D，K），计算每组参数对应的ENMS，取ENMS最小的一组为最优参数组。归一化均方误差与（D，K）构成的三维曲面图如图2所示。由图2可知，OMP算法和ST-AMP算法最优模型参数都是（4，3），此时，ENMS分别为-34.54dB和-34.93dB，达到内核参数计算精度。因此，所有实验都将以模型参数（4，3）作为训练基础。

3.2算法重构精度分析

在无噪情况下，分析对比OMP算法与ST-AMP算法的收敛性。当N=400时，归一化均方误差随迭代次数变化曲线如图3所示。由图3可以看出，在训练长度条件苛刻的情况下，OMP算法与ST-AMP算法的NMSE都随迭代次数的增大而减小，最后趋于稳定。OMP算法仅迭代10次后，ENMS即可收敛于-35.26dB，而ST-AMP算法则需迭代240次时，ENMS才趋于稳定，近似收敛于-35.86dB。两种算法相比，OMP算法收敛速度更快，而ST-AMP算法收敛稳定后ENMS更优。

归一化均方误差性能随训练样本长度变化曲线如图4所示，该曲线对比OMP和ST-AMP算法的ENMS性能。随着训练样本长度N的增加，两条曲线都逐渐趋于稳定。两者相比，ST-AMP算法在N=400时，可达到ENMS=-30dB，比OMP算法小1.85dB，可见ST-AMP算法在训练规模较小时，仍能保持较好的重构精度。继续增大N值，ST-AMP算法最终收敛于-33.78dB，而OMP算法最终收敛于-31.93dB，可见ST-AMP算法重构精度高于OMP算法。

设置样本长度N=400，对比上述两种算法计算的模型参数数量。确定模型参数（D，K）=（4，3），VS-NPE模型参数固定数量为84，ST-AMP和OMP计算所得参数数量分别为79和29，分别降低了6%和65%。可见OMP计算参数量减少最多，即通过OMP所得的VS-NPE模型结构最为简单，可有效降低硬件消耗。测试上述两种算法在含噪情况下NMSE性能，设置N=400，信噪比（signal-noiseratio，SNR）RSN为40dB时，ST-AMP和OMP对应的ENMS分别为-25.22dB和-25.45dB，证明了其在含噪情况下也可以正确重构VS-NPE内核系数。

3.3VS-NPE线性化能力

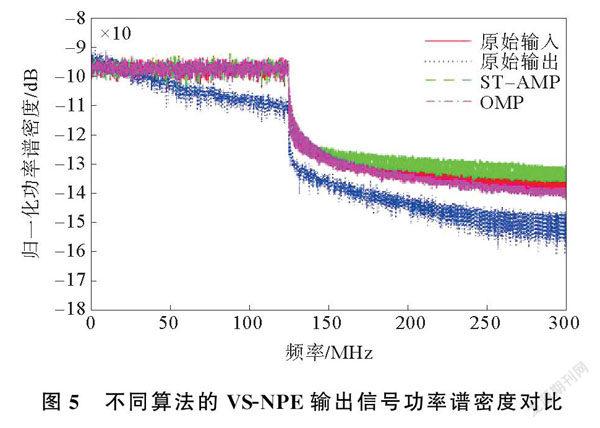
仿真分析所提方案的非线性补偿性能，可通过比较功率谱密度和误码率，直观地分析所提方案的功率谱密度，不同算法的VS-NPE输出信号功率谱密度对比如图5所示。图5显示了有均衡和无均衡情况下的接收信号功率谱密度。由图5可以看出，在无均衡的情况下，接收信号的带外和带内功率都不同程度的出现失真，且低频和高频部分严重衰减。在含有基于OMP和ST-AMP算法的均衡器的情况下，可有效地抑制接收信号带内、带外功率的失真，证明上述两个方案都具有较强的线性化能力。

當N=400，RSN=40dB时，基于不同算法构建相应的VS-NPE，对比其误码率性能，不同算法下VS-NPE的误码率曲线如图6所示。由图6可以看出，上述方案都具有较高的内核重构精度，OMP和ST-AMP两个方案下的误码率性能都比原版明显提升，其中ST-AMP算法在N=400的样本规模下误码率性能最佳，并且它可以降低每比特所需信噪比，当误码率达到10-3时，比OMP降低近6dB信噪比，证明其缓减信道非线性的能力优于OMP方案。

4结束语

本文利用CS重构算法OMP和ST-AMP计算VS-NPE内核参数，构造强健的VS-NPE模型以缓解VLC信道失真。ST-AMP算法是结合CS中AMP算法和LS算法，且为AMP的迭代过程引入阻尼因子和稳固阈值函数。仿真结果表明，当VS-NPE模型将参数（D，K）设置为最优时，OMP算法的优点是收敛速度快，且计算的模型内核数量少，可有效降低模型复杂度及硬件损耗。ST-AMP算法的优点是收敛稳定后NMSE更小，证明ST-AMP算法收敛时参数辨识精度更高。另外，在样本长度较小的苛刻条件下，两种算法仍能保持较高的重构精度。同时，分析OMP算法和ST-AMP算法所构建的VS-NPE在VLC系统中的线性化能力，归一化功率谱密度曲线证明上述两种算法下的VS-NPE都具有线性化能力，可同时补偿VLC信道输出信号的带内、带外非线性失真，但ST-AMP算法收敛速度仍存在不足，因此在后续工作中仍需对ST-AMP算法的迭代过程继续优化。

参考文献：

[1]ELGALAH，MESLEHR，HAASH.Non-linearityeffectsandpredistortioninopticalOFDMwirelesstransmissionusingLEDs[J].InternationalJournalofUltraWidebandCommunicationsandSystems，2009，1（2）：143150.

[2]STEPNIAKG，SIUZDAKJ，ZWIERKOP.CompensationofaVLCphosphorescentwhiteLEDnonlinearitybymeansofvolterraDFE[J].IEEEPhotonicsTechnologyLetters，2013，25（16）：15971600.

[3]QIANH，YAOSJ，CAISZ，etal.AdaptivepostdistortionfornonlinearLEDsinvisiblelightcommunications[J].IEEEPhotonicsJournal，2014，6（4）：18.

[4]MIAOP，ZHUB，QIC，etal.Amodel-drivendeeplearningmethodforLEDnonlinearitymitigationinOFDM-basedopticalcommunications[J].IEEEAccess，2019（7）：7143671446.

[5]MIAOP，QIC，FANGL，etal.DeepclippingnoisemitigationusingISTAwiththespecifiedobservationsforLED-basedDCO-OFDMsystem[J].IETCommunications，2018，12（20）：25822591.

[6]HAUPTJ，BAJWAWU，RABBATM，etal.Compressedsensingfornetworkeddata[J].IEEESignalProcessingMagazine，2008，25（2）：92101.

[7]CANDESEJ，WAKINMB.Anintroductiontocompressivesampling[J].IEEESignalProcessingMagazine，2008，25（2）：2130.

[8]BECERRAJA，MADERO-AYORAMJ，REINA-TOSINAJ，etal.Structuredcompressed-sensingforvolterraseriesmodels[C]∥2016IEEE17thAnnualWirelessandMicrowaveTechnologyConference.ClearWater，FL，USA：IEEE，2016：14.

[9]KEKATOSV，GIANNAKISGB.Sparsevolterraandpolynomialregressionmodels：recoverabilityandestimation[J].IEEETransactionsonSignalProcessing，2011，59（12）：59075920.

[10]DONOHODL，MALEKIA，MONTANARIA.Messagepassingalgorithmsforcompressedsensing：I.motivationandconstruction[C]∥2010IEEEInformationTheoryWorkshop.Cairo：IEEE，2010：15.

[11]TROPPJA，GILBERTAC.Signalrecoveryfromrandommeasurementsviaorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory，2007，53（12）：46554666.

[12]LIANGQ，LUX，LIANGS，etal.Performanceanalysisofspacemultiplexingbysuperposedsignalinmulti-dimensionalVLCsystem[J].OpticsExpress，2018，26（16）：1976219772.

[13]迟楠，张梦洁，施剑阳.可见光通信中LED非线性失真补偿算法研究[J].光學与光电技术，2015，13（5）：914.

[14]MIAOP，CHENG，WANGX，etal.Adaptivenonlinearequalizationcombiningsparsebayesianlearningandkalmanfilteringforvisiblelightcommunications[J].JournalofLightwaveTechnology，2020，38（24）：67326745.

[15]SCHETZENM.Nonlinearsystemmodelingbasedonthewienertheory[J].ProceedingsoftheIEEE，1981，69（12）：15571573.

[16]LIUX，MIAOP.Performanceinvestigationofvolterra-baseddigitalpredistortionusingorthogonalmatchingpursuit[C]∥2020InternationalConferenceonCommunications，InformationSystemandComputerEngineering.KualaLumpurMalaysia：CISCE，2020：6367.

[17]CHENWF，CHENLD，LVMJ，etal.IterativelyreweightedcomplexapproximatemessagepassingforISARimagingwithclustersparsestructure[C]∥IEEEInternationalConferenceonSignalProcessing，CommunicationsandComputing.Xiamen：ICSPCC，2017：14.

[18]MAJJ，LIP.OrthogonalAMP[J].IEEEAccess，2017，5：20202033.

[19]RANGANS，SCHNITERP，FLETCHERA，etal.Ontheconvergenceofapproximatemessagepassingwitharbitrarymatrices[J].IEEETransactionsonInformationTheory，2019，65（9）：53395351.

[20]芮国胜，刘歌，田文飚，等.基于二次最优阈值近似消息传递法的蒸发波导去噪重构[J].通信学报，2019，40（10）：1019.

[21]UYSALM，MIRAMIRKHANIF，NARMANLIOGLUO，etal.IEEE802.15.7r1referencechannelmodelsforvisiblelightcommunications[J].IEEECommunicationsMagazine，2017，55（1）：212217.

ResearchonVLCNonlinearEqualizerBasedonCompressedSensing

LIUXi，MIAOPu，TIANDaming

（TheCollegeofElectronicInformation，QingdaoUniversity，Qingdao266071，China）

Abstract：InordertosolveVolterraseriesnonlinearpost-distortionequalizer（VS-NPE）problemssuchasthelargenumberofcoresandcalculationdifficulties，thisstudyusestheorthogonalmatchingpursuit（OMP）algorithmandimprovedapproximatemessagepassing（AMP）algorithmtocalculateVS-NPEkernelparameters.WhentheimprovedAMPalgorithmisapplied，theVS-NPEmeasurementmatrixneedstobenormalized，andthentheAMPalgorithmiterativeprocessisintroducedintothedampingfactorsandthestablethresholdfunctiontoimprovetheaccuracyofmodelconstruction.Thesimulationresultsshowthatwhenthetrainingsamplelengthissmall，theOMPalgorithmandtheimprovedAMPalgorithmstillhavehighreconstructionaccuracy，andthenumberofmodelcorescalculatedbytheOMPalgorithmisreducedby65%，whicheffectivelyreducesthemodelcomplexity.Inaddition，theVS-NPEbasedontheabovetwoalgorithmsshowsgooddistortioncompensationinnormalizedpowerspectrumandbiterrorratio（BER）performance，whichprovetheeffectivenessandfeasibilityoftheproposedscheme.ThisresearchhelpstobuildarobustVS-NPEmodel，whichcansignificantlyalleviatethechannelnonlineardistortionofvisiblelightcommunication（VLC）systems.

Keywords：visiblelightcommunication;nonlinearequalizer;volterraseries;orthogonalmatchingpursuit

收稿日期：20211116;修回日期：20220110

基金项目：国家自然科学基金资助项目（61801257）;山东省自然科学基金资助项目（ZR2019BF001）

作者简介：刘希（1997），女，硕士研究生，主要研究方向为通信信息处理。

通信作者：苗圃（1987），男，副教授，主要研究方向為下一代通信系统关键技术。Email：mpvae@qdu.edu.cn