基于压缩感知的模拟信息转换器仿真
2015-07-21周权谌贵辉李瑞潘磊
周权+谌贵辉+李瑞+潘磊
摘 要:由于奈奎斯特采样定理的限制,在对高频率信号、大数据量、宽带跳频信号的采集时,传统的数据采集技术面临着巨大的挑战。近年国际上提出的压缩感知理论(Compressed Sensing)能有效缓解传统数据采集的压力,而以压缩感知理论为基础的模拟信息转换器能直接对连续模拟信号以远低于奈奎斯特采样频率进行采样,最后通过相关的重构算法对原信号进行精确重构。文中对压缩感知理论及模拟信息转换器理论进行了介绍,并通过Matlab对模拟信息转换器进行了仿真验证。
关键词:压缩感知;模拟信息转换器;正交匹配追踪算法;Matlab
中图分类号:TN957.52 文献标识码:A 文章编号:2095-1302(2015)07-00-02
0 引 言
现代技术的飞速发展导致数据量的急剧增多,传统的奈奎斯特采样定理大大限制了数据的采集、存储,及增加硬件的成本。根据传统采样方法,采样速率要高于信号带宽的两倍及以上才能还原原信号,而在实际工程应用中,常采用大于两倍的采样频率。
近几年出现了一种新的理论:压缩感知(也称压缩采样)[1]。该理论表明:如果信号是稀疏的,或者在某变换域下是稀疏的,则可以用一个与变换基不相关的观测矩阵来对原始信号进行线性投影,然后对投影得到的测量值通过求解优化问题,可高概率的实现原始信号的重构[2]。模拟信息转换器是压缩感知理论的实际应用之一,使系统能够以远低于奈奎斯特采样频率进行采样,经过重构算法,使采样得到的信号能大概率的精确重构。
1 压缩感知理论原理
一长度为N的实值有限长一维离散信号x(x∈RN),RN空间里的任何信号都可以用基向量Ψ线性表示,则x可以表示为:
或者 x=θΨ (1)
其中θ=[θi]=[
Y=Φx=ΦΨθ=ACSθ (2)
式中ACS=ΦΨ=Θ称为恢复矩阵[3]。
由于恢复矩阵ACS=ΦΨ=Θ是个M×N(M×N)的矩阵,方程Y=ACSθ为欠定方程组,方程的个数小于未知数的个数,方程无确定解,无法重构信号。为了保证从观测值准确重构信号,观测矩阵Φ需要满足两个条件限制[6]:
(1)观测矩阵Φ和基矩阵Ψ之间的不相干性;
(2)RIP(有限等距约束):对于任意K稀疏的信号x和常数δK∈(0,1),恢复矩阵Θ=ΦΨ满足:
(3)
实际应用中观测次数M≥c·Klog(N/K),则构建的观测矩阵Φ在很大概率上同时满足不相干性和有限等距约束条件。
2 模拟信息转换器结构模型
基于压缩感知理论构建模拟信息转换器有两个问题需要解决:
(1)压缩感知理论的提出是针对于离散信号;
(2)从硬件上实现多维矩阵相乘运算比较困难。
对于以上问题需要找到一种能从连续信号中得到离散信号的方法。由此Saini Kirolos等人提出了一个基于压缩感知理论应用于模拟信号处理的方案,即模拟信息转换器(AIC)[4]。
假设模拟信号x(t)(t∈[0,T])可由一些连续函数构成的字典中的有限个函数进行线性表示:
(4)
αn是线性表示的系数,且αn中只有很少的几个大系数,我们可以说x(t)是可压缩的。表达字典中的函数ψn可能带宽很大,但信号的自由度比较小,所以我们能以几倍于信号的自由度进行采样,而不是以两倍及以上信号带宽的奈奎斯特采样频率进行采样。系统框图如图1所示[4]:
图1 AIC系统框图
AIC系统由调制、滤波、均匀采样等三大部分组成,其中x(t)用伪随机PN序列Pc(t)∈{-1,1}进行调制,Pc(t)符号改变的速率必须大于奈奎斯特采样频率,调制的目的是为了后期的信号重构提供必要的随机性。调制后的信号通过低通滤波器滤波,滤波后的信号最后通过采样速率为M的普通ADC进行采样。观测值Y可以看为离散系数矢量α的线性变换,类似于离散信号的压缩感知理论,其线性变换过程包含两个过程:第一是离散矢量α被表达字典Ψ投影成模拟信号x (t);第二是模拟信号x(t)被观测矩阵Φ投影成离散矢量Y。系统输出y[m]可以表示为:
(5)
将代入式(5)有:
(6)
假设θm,n∈Θ,则:
(7)
即有表达式:y=Θα。
此时,模拟信息转换器模型与离散信号的压缩感知理论达到了形式上的统一[5]。
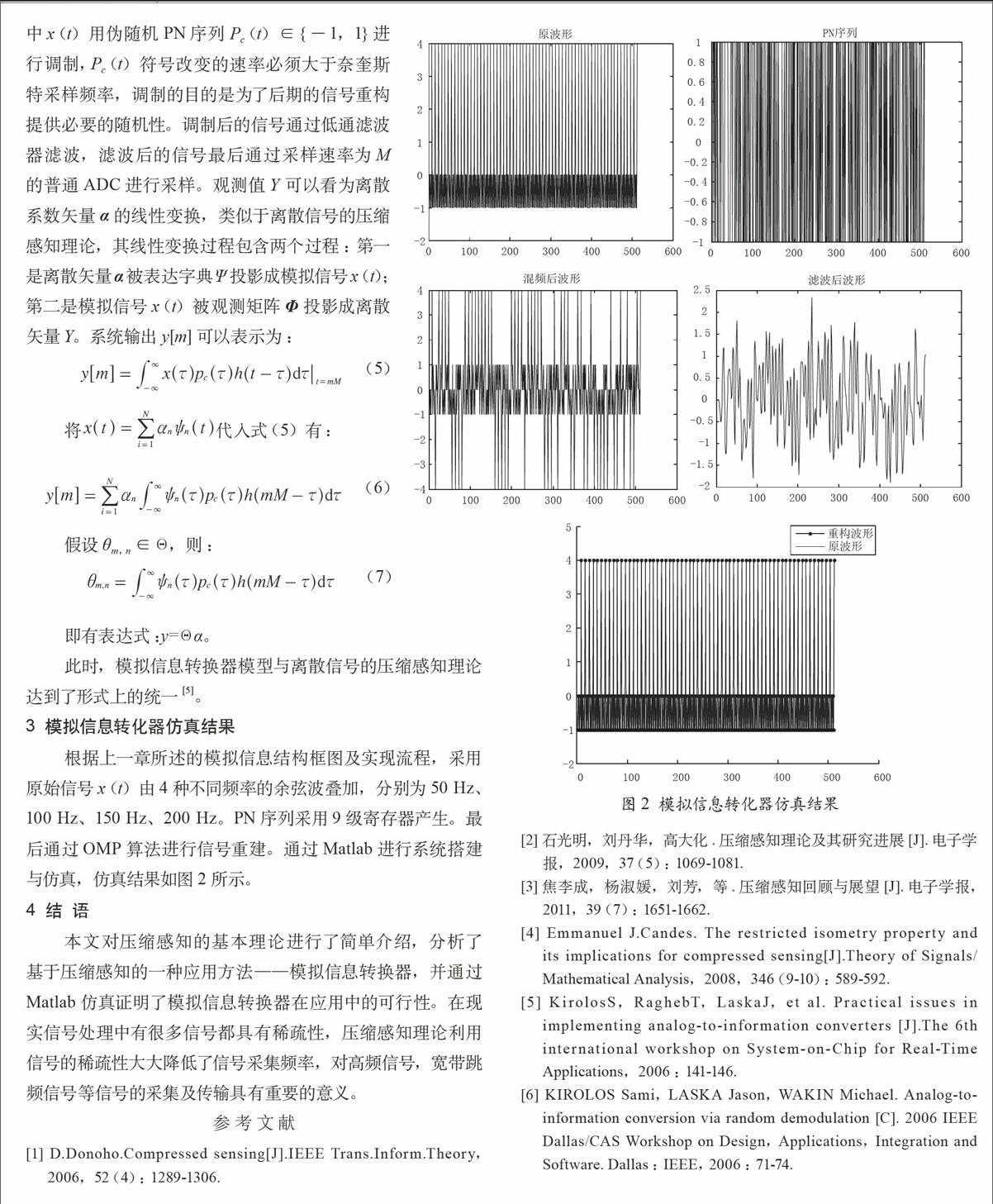
3 模拟信息转化器仿真结果
根据上一章所述的模拟信息结构框图及实现流程,采用原始信号x(t)由4种不同频率的余弦波叠加,分别为50 Hz、100 Hz、150 Hz、200 Hz。PN序列采用9级寄存器产生。最后通过OMP算法进行信号重建。通过Matlab进行系统搭建与仿真,仿真结果如图2所示。
4 结 语
本文对压缩感知的基本理论进行了简单介绍,分析了基于压缩感知的一种应用方法——模拟信息转换器,并通过Matlab仿真证明了模拟信息转换器在应用中的可行性。在现实信号处理中有很多信号都具有稀疏性,压缩感知理论利用信号的稀疏性大大降低了信号采集频率,对高频信号,宽带跳频信号等信号的采集及传输具有重要的意义。
参考文献
[1] D.Donoho.Compressed sensing[J].IEEE Trans.Inform.Theory,2006,52(4):1289-1306.
[2]石光明,刘丹华,高大化.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1069-1081.
[3]焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1651-1662.
[4] Emmanuel J.Candes. The restricted isometry property and its implications for compressed sensing[J].Theory of Signals/Mathematical Analysis,2008,346(9-10):589-592.
[5] KirolosS,RaghebT,LaskaJ,et al. Practical issues in implementing analog-to-information converters [J].The 6th international workshop on System-on-Chip for Real-Time Applications,2006:141-146.
[6] KIROLOS Sami, LASKA Jason, WAKIN Michael. Analog-to-information conversion via random demodulation [C]. 2006 IEEE Dallas/CAS Workshop on Design, Applications, Integration and Software. Dallas: IEEE, 2006: 71-74.