一种基于卡尔曼滤波的相关干涉仪改进算法

李瑞霖　赵文鹏　张书哲　迟宗涛

文章编号：10069798（2022）02001406;DOI：10.13306/j.10069798.2022.02.003

摘要：针对相关干涉仪算法在户外建库时因受到环境白噪声和同频多径干扰导致测量精度低的问题，本文提出了一种基于卡尔曼滤波的相位模板库处理方法。通过分析相关干涉仪理论和卡尔曼滤波理论，证明了相关干涉仪相位模板库建立过程是卡尔曼滤波的典型使用场景，给出了基于卡尔曼滤波的相位模板库的处理方法及具体流程。同时，对白噪声干扰和同频多径干扰两种场景下的卡尔曼滤波，采用Matlab进行了算法仿真。仿真结果表明，基于卡尔曼滤波的相位模板库处理方法，可以对多径干扰下的相位模板库进行优化，达到相关干涉仪的使用标准，证明了该方法的有效性。该研究具有广泛的应用前景。

关键词：

卡尔曼滤波;相关干涉仪;相位模板库;白噪声;多径噪声

中图分类号：TN99;TP751.1文献标识码：A

近年来，射频信号（radiofrequencysignal，RF）准确定位问题逐渐成为定位领域的研究热点，应用场景广泛[13]。相关干涉仪（correlationinterferometer，CI）现已发展为较成熟的定位体制，根据入射信号到达不同天线阵元时，空间上接收到的相位不同，进而确定目标方向，具有造价低、稳定性好、隐蔽性强等优点[47]。传统的相关干涉仪算法对使用环境要求较高，相位模板库一般在微波暗室中建立，但微波暗室造价高，大部分单位都不具备微波暗室的实验条件，且微波暗室的体积也进一步限制了更多电磁场景模相位模板库的建立。而在普通电磁环境的情况下建立相位模板库，会引入环境噪声，如高斯噪声和同频多径信号干扰等，降低了模板库的可使用性。应用吸波材料是对抗多径效应较好的解决方法[8]，将其置于相关干涉仪天线阵列外围，可以阻挡一定角度范围内的多径信號[911]，但添加吸波材料会大幅削弱天线阵元旁瓣，从而减弱目标信号，同时吸波材料无法做到信号的完全吸收，可能会造成天线阵内反射问题。在无线通信领域，分集接收技术是一种常用的对抗多径干扰的技术[12]，但主要针对信号的复原，并不能很好的应用于定位技术。在室内定位和卫星定位领域，多径效应同样是影响定位精度的重要干扰因素[1315]，但可以通过极为精确的时钟同步技术解决多径问题，如到达时间（timeofarrival，TOA）、到达时间差（timedifferenceofarrival，TDOA）以及超前滞后延迟锁定环（early-minus-lateloop，EML）、前后斜率差技术（earlylateslopetechnique，ELS）、高分辨率相关法（highresolutioncorrelator，HRC）等技术[1619]，但这些技术同样难以应用在相关干涉仪测向领域。基于此，本文提出了一种基于卡尔曼滤波的相关干涉仪测向算法，通过优化相位差库，很好的解决了相关干涉仪定位中的多径效应问题。将该算法应用于相位差库建立过程中，保证了相关干涉仪的实时稳定。该算法为相位差库的建立提供了参考依据。

1相关干涉仪和卡尔曼滤波

1.1相关干涉仪

相关干涉仪测向的基本原理是通过无线电信号，相对于天线阵列参考方向的角度与天线阵元间信号的相位关系，推论无线电信号的入射角度[20]。具体实现方法是将当前采集的信号与在相同环境下建立的相位差模板库进行对比，相关度最高的角度为测量结果。

以多阵元相关干涉仪为例，建立数学模型。假设测向天线为N阵元L阵列，则阵元n（n=1，2，…，N）在t时刻接收的信号可表征为

其中，an（t）为t时刻阵元n接收信号的幅值;φn（t）为信号相位;e为自然常数;j为虚数单位;Δn（t）为阵元接收噪声在相位值上的体现，呈高斯分布，其方差σ主要取决于接收信号的信噪比（signalnoiseratio，SNR），即RSN，近似为σ=1/2RSN。

对于入射方向为（θ，ψ）的信号，相位差表示为不同天线阵元接收信号的相位差。阵元m与阵元n接收信号的相位差为

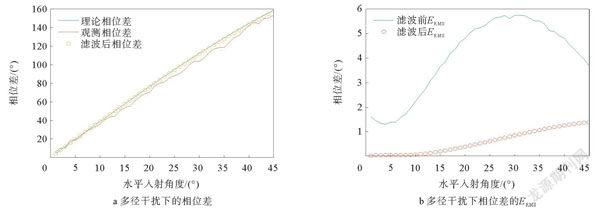
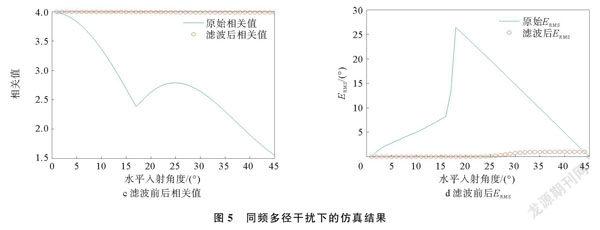
其中，θ为入射信号的水平方向;ψ为入射信号的入射方向;m为阵元序号，m=1，2，…，N-1，m

通过接收不同入射方向的信号，提取相位差，得相位模板库为

在测向阶段，将接收到的信号提取相位差Φr=a1，2a1，3…am，n（m=1，…N-1;n=m+1，…，N）后，与模板库中每个角度的相位差矩阵作相关运算，得相关值为

式中，coe为相关系数。使相关值达到最大的方向值即为入射方向

1.2卡尔曼滤波

1960年，卡尔曼提出了一种最优线性状态估计方法＼[21＼]，即卡尔曼滤波器。该方法最大的优点是采用递归的方法解决线性滤波问题，只需当前的测量值和前一个采样周期的估计值就能进行状态估计＼[17＼]。

卡尔曼滤波的核心公式分别为

式（6）和式（7）表示对k时刻的测量值和协方差的先验估计。其中，x︿k-1为k-1时刻的后验状态估计值，也表示k-1时刻的最优估计值;x︿k-为k时刻的先验估计值，即根据k-1时刻的最优估计值对k时刻的预测结果;A为状态转移矩阵，表示对目标状态转换的一种猜想模型;B为可选的控制输入uk-1的增益;Pk-为k时刻先验估计协方差，即x︿k-的协方差;而Pk-1表示k-1时刻后验估计协方差，即x︿k-1的协方差;Q为系统过程的协方差，表示状态转换矩阵与实际过程之间的误差。式（8）表示对卡尔曼增益的计算，其中，H是状态变量到测量的转换矩阵，表示将状态和观测连接起来的关系;R为测量噪声协方差，可在实际实现时进行观测。式（9）和式（10）表示对k时刻数值和协方差的后验估计，其中，x︿k为k时刻后验状态估计值;zk为实际测量值;Pk表示k时刻后验估计协方差。因此，只要提供每个时刻的测量值，优化估计就能持续进行。

1.3基于卡尔曼滤波的相关干涉仪算法

相关干涉仪算法是在建立相位模板库时，通过布置条件确定实验场景，也就是根据信号的入射方向、频率及天线阵列的排布等条件，推导出角度变化时天线阵元间接收相位差的数学模型。相位模板库是通过等间隔的角度变化建立，如以1°为间隔进行采集，按序采集水平角度1°～45°的信号，并从中提取相位差进行存储。在此，以信号的入射角度代替离散时间系统中的时间变量。通过下文的推导可知，该状态转换过程是确定的。

以某角度天线阵元间的理论相位差为系统状态变量，将接收到信号的相位差作为观测变量，状态转换过程确定，被估计过程和观测变量与过程的关系是线性的，可以应用卡尔曼滤波算法。算法流程如图1所示。

本研究以一个L天线阵列为例，信号入射图如图2所示。在相关干涉仪建立相位模板库过程中，构建不同角度天线阵元间的理论相位差值的数学模型。其中，A、B、O为天线阵元，设入射信号的水平角度为θ，俯仰角度为ψ，则入射信号方向为（θ，ψ），阵元O与阵元A及阵元B之间的相位差为

式中，β=arctan（tanψcosθ），表示中间角度;lOA为阵元O与阵元A中心距离;lOB阵元O与阵元B中心距离;λ为入射信号的波长。通过计算可得不同入射角度天线阵元间的理论相位差值，以及以角度为变量的系统状态变量。由仿真结果可知，在俯仰角度固定的情况下，当水平角度在0°～45°时，相位差的变化近似于线性变化，状态转换过程看作是确定的。

2仿真验证

利用相关干涉仪算法在室外建立相位差模板库时，主要受高斯噪声和同频多径噪声的影响，导致其适用性差。针对两种噪声干扰，对模板库进行卡尔曼滤波，探究该方法的滤波效果。选取5元天线阵列作为相关干涉仪的信号接受部分，5元天线阵列示意图如图3所示，其中，1～5表示5个天线阵元，其间距L12、L23、L14、L45由解模糊算法确定＼[4＼]。以1°為间隔，建立相位模板库，由于不同频率的测向过程相同，这里仅选取频率为1.7GHz的信号进行仿真验证。

2.1高斯白噪声下的仿真实验

对仅有高斯噪声干扰的情况进行仿真实验，得到卡尔曼滤波对相位差模板库的滤波效果。设置俯仰角度为0°，水平角度为1°～5°，接收信号的信噪比为20dB，噪声为高斯白噪声。

一次建库过程中，在白噪声下，天线阵元1和2之间相位差仿真结果如图4所示。在20dB的噪声干扰下，接收信号明显偏离，在卡尔曼滤波后，滤除了大部分奇异点，相差明显接近理论值。为了进一步验证滤波的稳定性与适应性，在此条件上进行1000次蒙特卡洛实验，使用每个方位点上相位差与理论相差的均方根差值（root-meansquareerror，RMSE），即ERMS（φ）体现滤波效果。

其中，φi是相位差的理论值;φc是第C次实验时的相位差，C=1000。均方根差值越小，表示滤波效果更好。由图4可以看出，经过卡尔曼滤波后，天线阵元1和阵元2相位差均方根误差由5°左右降低到1°左右。

相关干涉仪经过1000次蒙特卡洛实验，得到滤波前后相关值和ERMS结果，角度为（θout，ψout）的相关值越高，表示接收信号与相位模板库（θout，ψout）的匹配度越高，经过滤波后，相关值都接近最大值4。由图4d可以看出，均方根误差从0.7°左右降低到0°左右。均方根误差为

其中，θr和ψr为入射信号的真实方位。ERMSout越小，表示结果的准确率越高。仿真结果表明，卡尔曼滤波对白噪声干扰的滤波效果明显，经过滤波后的相关干涉仪算法效果提升。

2.2同频多径干扰下的仿真实验

在高斯噪声的基础上，同频多径噪声对相位模板库也会产生影响，对卡尔曼滤波的滤波效果进行仿真实验。入射信号在30dB信噪比的基础上，添加同频多径信号的干扰，最终的信噪比是20dB。多径信号的方向为θ，ψ=（4°，1°），其它仿真条件不变，同频多径干扰下的仿真结果如图5所示。由图5可以看出，同频多径信号对相关干涉仪算法影响较大，与白噪声不同，同频多径信号会直接导致严重错误。图5a为天线阵元1和阵元2间的相位差，图5b为多径干扰下的相位差ERMS。由图5a和图5b可以看出，多径干扰会造成相位差朝一个方向明显偏离，导致相关干涉仪结果明显偏移，无法使用，但经过卡尔曼滤波，偏移得到明显的修正。

图5c和图5d是经过1000次蒙特卡洛实验后，滤波前后相关值和ERMS。由图5c和图5d可以看出，多径干扰造成的后果相当严重，而经过对相位差偏移的修正，相关干涉仪可以重新正常工作，最终测向结果误差小于2°。

仿真结果表明，基于卡尔曼滤波的处理方法可以对多径干扰下的相位模板库进行优化，达到相关干涉仪的使用标准。

3结束语

本文在分析卡尔曼滤波和相关干涉仪建库过程的基础上，介绍了一种基于卡尔曼滤波的相关干涉仪相位模板库的优化方法，并采用Matlab进行仿真分析。仿真结果表明，该算法应用在相位差库建立过程中，与优化前的算法相比，保证了相关干涉仪的实时稳定，对建库过程中的白噪声干扰及同频多径噪声干扰均有较好的滤波效果，可应用于非微波暗室下建立相位模板库的场景。在接下来的研究中，将使用多种优化卡尔曼滤波算法，实现精度的再提升，并将通过实验证明其有效性。

参考文献：

[1]蔡丽萍，胡家良，陈海华，等.改进相关干涉仪算法在DOA估计中的应用[J].计算机系统应用，2018，27（12）：129135.

[2]刘源，王洪先，纠博，等.米波MIMO雷达低空目标波达方向估计新方法[J].电子与信息学报，2016，38（3）：622628.

[3]李统乐，李海英，徐彬，等.VHF雷达回波距离拓展特性频率依赖关系研究[J/OL].电波科学学报：17[20210720].http：∥kns.cnki.net/kcms/detail/41.1185.TN.20210719.1511.001.html.

[4]刘满朝，刘乐.二维干涉仪测向技术研究[J].现代雷达，2018，40（2）：4448.

[5]王秋滢，匡春旭，钟万青.MIMU辅助无人机相关干涉仪测向方法研究[J].计算机仿真，2021，38（2）：5257.

[6]刘俊，朱全江，杨南.干涉仪测向天线阵相关性分析与优化设计[J].电子信息对抗技术，2020，35（6）：8387.

[7]高婕，牛刚，杜太行，等.超短波多径信号相关干涉仪测向算法[J].兵工学报，2020，41（11）：22522259.

[8]刘路，刘峰，李峰.密闭狭小环境中多径信号对码环的影响[J].电子设计工程，2015，23（16）：6264.

[9]韩敏阳，韦国科，周明，等.低频雷达吸波材料的研究进展[J/OL].复合材料学报：113[20210910].https：∥doi.org/10.13801/j.cnki.fhclxb.20210909.010.

[10]周伟，张玉婷，王晶晶，等.SiCnf-Cf/Si3N4復合材料的微观结构与吸波性能[J].硅酸盐学报，2021，49（9）：19161927.

[11]WANGW，ZHANGS，PANYQ，etal.Wave-absorbingmaterialaidedmicrowavefreeze-dryingofvitaminCsolutionfrozenwithpreformedpores[J].DryingTechnology，2020，39（13）：20252038.

[12]陈永欣.浅谈分集接收技术与RAKE接收机[J].电信网技术，2002（5）：35.

[13]刘晨，刘开琦，华宇.基于BOC调制的伪卫星抗多径性能研究与分析[J].电子设计工程，2021，29（19）：168173.

[14]熊智敏，王党卫，李星辉，等.多径条件下米波OFDM-MIMO雷达波束性能及特性分析[J].国防科技大学学报，2021，43（4）：136144.

[15]李方伟，鲁佳文，王明月.多径环境下联合时间反演和PCA降维的阵列幅相误差校正[J].通信学报，2021，42（8）：111119.

[16]钱潮.高精度室内多维定位算法研究及实验验证[D].南京：东南大学，2019.

[17]王伟.GNSS软件接收机的多径及弱信号处理与定位方法研究[D].镇江：江苏大学，2017.

[18]SCHMIDTE，GATSISN，AKOPIAND.High-resolutioncorrelatorbaseddetectionofGPSspoofingattacksusingtheLASSO＼[C＼]∥2020IEEE/IONPosition，LocationandNavigationSymposium.Monterey，USA：IEEE，2020：11961201.

[19]蔡丽萍，胡家良，陈海华，等.改进相关干涉仪算法在DOA估计中的应用[J].计算机系统应用，2018，27（12）：129135.

[20]KALMANRE.Anewapproachtolinearfilteringandpredictionproblem[J].TransactionoftheASME-JourhalofBasicEngineering，1960，82：3545.

[21]王学斌，徐建宏，张章.卡尔曼滤波器参数分析与应用方法研究[J].计算机应用与软件，2012，29（6）：212215.

AnImprovedAlgorithmofCorrelationInterferometerBasedonKalmanFilter

LIRuilin，ZHAOWenpeng，ZHANGShuzhe，CHIZongtao

（TheCollegeofElectronicInformation，QingdaoUniversity，Qingdao266071，China）Abstract：

Aimingattheproblemoflowmeasurementaccuracycausedbyenvironmentalwhitenoiseandcofrequencymultipathinterferencewhenthecorrelationinterferometeralgorithmisbuildingalibraryoutdoors，thispaperproposesaphasetemplatelibraryprocessingmethodbasedonKalmanfiltering.ByanalyzingthetheoryofthecorrelationinterferometerandtheKalmanfiltertheory，itisprovedthattheprocessofestablishingthephasetemplatelibraryofthecorrelationinterferometerisatypicalusescenariooftheKalmanfilter，andtheprocessingmethodandspecificprocessofthephasetemplatelibrarybasedontheKalmanfilteraregiven.AimingattheKalmanfilteringinthetwoscenariosofwhitenoiseinterferenceandco-frequencymultipathinterference，thealgorithmsimulationiscarriedoutusingMatlab.ThesimulationresultsprovetheeffectivenessofthephasetemplatelibraryprocessingmethodbasedonKalmanfilter.Theresearchhasawiderangeofapplicationscenarios.

Keywords：Kalmanfilter;correlationinterferometer;phasetemplatelibrary;whitenoise;multipathnoise

收稿日期：20211027;修回日期：20211219

作者简介：李瑞霖（1997），男，硕士研究生，主要研究方向为信息获取与传感器技术。

通信作者：迟宗涛（1964），男，教授，硕士生导师，主要研究方向为信息获取与传感器技术、电子测量与电子计量、仪器仪表和光电应用技术。Email：zoc545s@163.com