改进Oliver-Pharr法在铁电单晶纳米压痕中的应用

张伟光，李继军,2，杨诗婷，侯小虎，邢永明

（1. 内蒙古工业大学 理学院，内蒙古 呼和浩特 010051；2. 上海海事大学 文理学院，上海 201306； 3. 内蒙古工业大学 测试中心，内蒙古 呼和浩特010051）

0 引言

纳米压痕技术也称深度敏感压痕技术，在科学研究及工业制造领域都得到了广泛的应用[1-5].纳米压痕技术作为一种测试微纳米尺度力学性能的重要手段，它具有分辨率高、可视化程度高、稳定性强以及试样制备简单等优点[6-10]，可以获得材料的弹性模量、硬度、断裂韧性等力学性质，适用于金属[11-13]、陶瓷[7,14-15]，以及微机电系统中的其他功能材料[16-18]的力学测试.

纳米压痕技术通常采用Oliver-Pharr[19]法，从弹性接触理论出发，给出描述纳米压痕实验位移-载荷曲线的经验公式，利用该经验公式得出接触刚度，计算出弹性模量和硬度.Oliver-Pharr法是根据卸载曲线起始点的斜率计算接触刚度的，只能得到最大深度处对应的硬度和弹性模量，无法给出力学参数随压入深度连续变化的曲线关系.在纳米压痕测试中，还需要准确校正压头接触投影面积[20].而压头接触投影面积受材料性质和压头磨损等因素影响，准确校正接触投影面积比较困难.

本文提出了改进Oliver-Pharr法，并利用该方法分析了PIN-PMN-PT铁电单晶纳米压痕数据，将计算结果与连续刚度测量（Continuous Stiffness Measurement，CSM）法的测量结果进行了比较，验证了该方法在分析纳米压痕数据时的可行性和有效性.

1 理论方法

纳米压痕实验中，接触刚度S与压头的接触投影面积A和弹性模量E之间的关系为

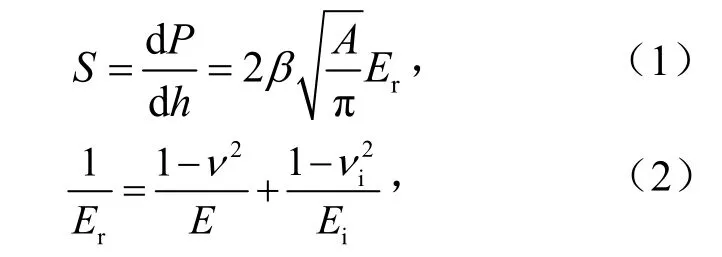
式中，β为与压头形状有关的常数；Er为折合模量，GPa；E为待测试样的弹性模量，GPa；ν为待测试样的泊松比；Ei为压头的弹性模量，GPa；νi为压头的泊松比.对于金刚石Berkovich压头β=1.034，Ei=1 141 GPa，νi=0.07.

在Oliver-Pharr方法中，纳米压痕卸载深度h与载荷P满足如下关系

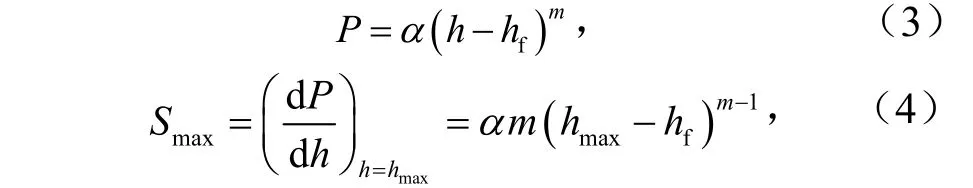
式中，α、m为拟合参数；hf为卸载后的残余深度，nm，可通过拟合得到；Smax为最大压入深度处的接触刚度，mN/nm.根据经典弹性接触理论[21]，幂律指数m的典型解为：圆柱型压头取1，抛物型压头取1.5，锥型压头取2.

考虑实际纳米压痕实验中弹塑性失配导致的塑性压痕与周围弹性基体间的残余接触应力的影响[22]，对式（3）引入虚拟载荷P0，则有

式中，α2为拟合参数；P0为虚拟载荷，mN.

虚拟载荷的引入是考虑压头完全卸载后，由于不可逆塑性变形的约束，塑性压痕下仍然会存在一定程度的弹性变形，这种残余弹性形变会使压痕表面沿加载方向的行为就像用到P0预加载的弹簧一样.式（5）在描述卸载曲线方面与式（3）一样有效.

根据弹性接触理论，当一定几何形状的压头压入理想的半无限弹性空间时，会存在一个与峰值载荷的大小无关的h-P关系[19].式（3）和式（5）中参数都依赖于峰值载荷，因此使用式（3）和式（5）只能确定最大载荷处的接触刚度.

对于理想的Berkovich压头，根据压头的几何形状给出接触投影面积A与接触深度hc的关系为

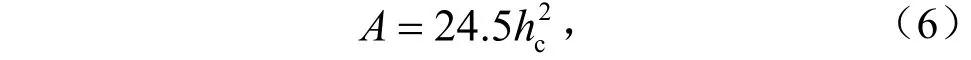
由于纳米级压头加工研磨技术的局限性和使用磨损，实际压头不可能是理想几何形状的，压头尖端往往偏离理想情况.这就导致在浅压入深度处真实接触投影面积函数与理想情况存在较大的差异.因此，需要在理想面积函数基础上校正实际压头的面积函数.通常，在使用过程中首先在标准试样熔融硅上设置一系列深度不同的压痕，拟合为

式中，C0，C1，…，C8为拟合参数.在纳米压痕实验前，需要采用标准试样熔融硅对面积函数进行校正.一旦压痕的接触刚度S和真实接触投影面积A确定，通过式（1）和式（2）可计算出待测试样的弹性模量.硬度为

将式（5）改写为二阶多项式

式中，α0、α1和α2为拟合参数.再对式（9）进行归一化处理得到

将式（10）代入式（1）可得

式（11）反映了最大压入深度处的接触刚度Smax与Pmax/hmax成正比.

对于纳米压痕加载阶段的任意数据（Parb，harb），如果（α1+2α2）为常数，任意加载过程中的接触刚度为

利用式（12），在不需要预先校正压头面积函数的情况下，可连续确定接触刚度.

2 材料及实验

实验材料选用 28Pb(In1/2Nb1/2)O3-43Pb (Mg1/3Nb2/3)O3-29PbTiO3（PIN-PMN-PT）铁电单晶，由中国科学院上海陶瓷研究所提供，并将PIN-PMN-PT单晶切割成尺寸为6 mm×4 mm× 0.5 mm的长方形试样.主平面6 mm×4 mm的法向是[111]晶向.对PIN-PMN-PT单晶试样的主平面进行机械和电解抛光，使其达到光滑镜面效果.

PIN-PMN-PT铁电单晶的纳米压痕实验在Nano Indenter G200纳米压痕仪上（Agilent，USA）进行，其载荷的分辨率为50 nN，最大载荷为500 mN.实验采用金刚石三棱锥Berkovich压头，压头的尖端曲率半径小于20 nm.实验采用CSM方法在室温下进行.实验参数为：谐波位移为2 nm，频率为45 Hz，应变速率为0.05 s-1.实验最大压入深度设定为500 nm、1 000 nm、1 500 nm、2 000 nm和2 500 nm.对每一最大压入深度测试5个点的数据.为了避免每一压痕相互不受干扰，压痕间的距离设定为100 μm.在每一设定最大压入深度处，保持载荷时间为10 s.

3 结果与讨论

3.1 位移-载荷曲线分析

图1给出了PIN-PMN-PT铁电单晶在不同最大压入深度500 nm到2 000 nm的压入深度-载荷（h-P）曲线.从图1中可以看出PIN-PMN-PT铁电单晶纳米压痕压入深度-载荷曲线离散度小、重复度很高，表明数据的准确性高.

图1 压入深度-载荷曲线 Fig.1 indentation depth-load curve

图2给出了最大压入深度为2 000 nm的保载阶段曲线.从图2中可以清晰地看出卸载部分的最大压入深度hmax2大于加载部分的最大压入深度hmax1.需要指出的是，Olive-Pharr法确定接触刚度是用的卸载部分的最大压入深度hmax2，而不是加载阶段的最大压入深度hmax1；而式（10）和式（11）中用到的是加载阶段的最大压入深度hmax1.

图2 保载阶段压入深度-载荷 Fig.2 loading depth-load in holding stage

根据式（10）分析PIN-PMN-PT铁电单晶纳米压痕实验卸载数据，计算参数α0、α1和α2的最佳拟合值，结果见图3.从图3可以看出，随着最大压入深度hmax的增加，α0和α2缓慢增加；α1明显减小.但在整个最大压入深度hmax变化范围内，2α2+α1和α1+α1+α2基本不变，其值分别为6.40和1.

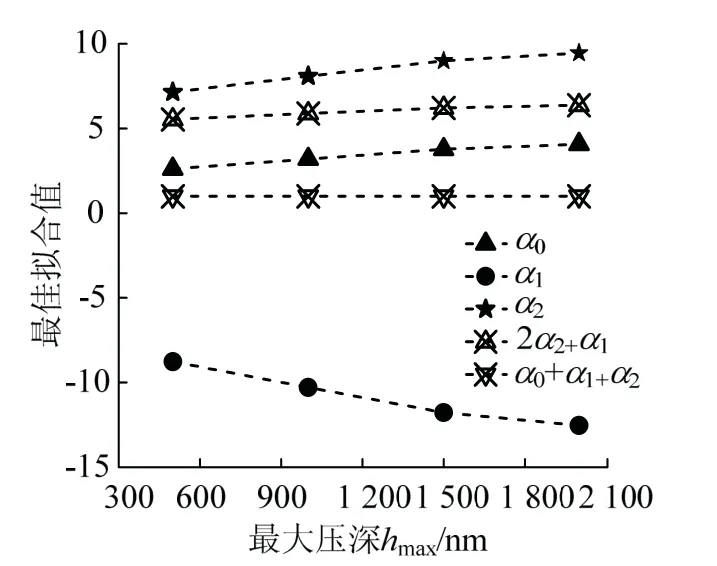
图3 各参数与最大压入深度关系 Fig.3 relationship between each parameter and maximum indentation depth

图4给出了PIN-PMN-PT铁电单晶纳米压痕实验中的残余深度和最大压入深度关系.

图4 残余深度与最大压入深度关系 Fig.4 relationship between maximum indentation depth and residual depth

图5给出了PIN-PMN-PT铁电单晶纳米压痕实验中上述引入的虚拟载荷和最大压入载荷的关系.

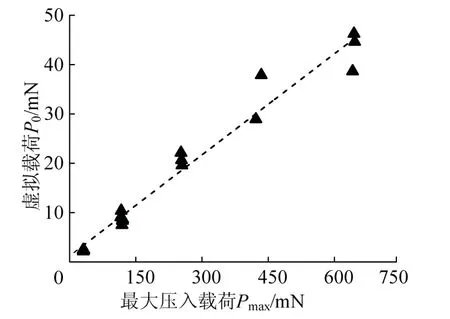
图5 虚拟载荷与最大压入载荷关系 Fig.5 relationship between maximum indentation load and virtual load

从图4、图5中发现残余深度和最大压入深度呈线性关系；虚拟载荷和最大压入载荷可以近似视为线性关系.这种线性关系与经典弹性接触理论[21]是一致的.这也说明在考虑塑性压痕与周围弹性基体间残余接触应力影响的基础上，引入虚拟载荷，提出的改进Oliver-Pharr法，即式（5）是合理的.

3.2 接触刚度分析

运用式（10），对图1中的每一条卸载曲线h-P数据进行拟合，求得参数α0、α1和α2的最佳拟合值，然后再根据式（11）计算每一个最大压入深度处的接触刚度.在Oliver-Pharr法中，使用式（3）对卸载曲线拟合，再通过式（4）导出最大压入深度处的接触刚度. 2种方法的运算结果显示，2组接触刚度值吻合很好，这也证实改进Oliver-Pharr法不会导致PIN-PMN-PT铁电单晶纳米压痕卸载曲线最大压入深度处的接触刚度发生显著变化.

通过式（5）对PIN-PMN-PT铁电单晶纳米压痕实验的各h-P曲线的卸载数据进行分析，然后使用拟合参数α2、hf和P0计算出接触刚度，即初始卸载斜率.不同最大深度处的接触刚度S随每个测试点的Pmax/hmax变化情况见图6.从图6中可见，PIN-PMN-PT铁电单晶纳米压痕实验的最大深度处的接触刚度S与Pmax/hmax呈线性关系，斜率为6.46，并与2α2+α1值一致.

图6 接触刚度与最大压入载荷、最大压入深度比的关系 Fig.6 relationship between contact stiffness and maximum indentation load and maximum indentation depth ratio

根据式（12）使用纳米压痕加载阶段的实验数据连续确定接触刚度.图7为接触刚度计算值与实验值对比结果.从图7中可见，改进的Oliver-Pharr方法计算的接触刚度与CSM方法结果吻合的很好.用改进Olive-Pharr法计算的接触刚度与压入深度呈线性关系，这种线性关系也证明式（12）分析PIN-PMN-PT铁电单晶纳米压痕数据有效.

图7 接触刚度计算值与实验值对比 Fig. 7 comparison between calculated and experimental values of contact stiffness

3.3 弹性模量和硬度分析

采用改进Oliver-Pharr法计算PIN-PMN-PT铁电单晶的弹性模量，同时给出了CSM的测量结果，见图8.

图8 弹性模量计算值与实验值对比 Fig.8 comparison between the calculated and experimental values of elastic modulus

由图8可见，压入深度小于200 nm，PIN-PMN-PT铁电单晶的弹性模量随着压入深度的增加迅速减小；压入深度大于200 nm，弹性模量的减小趋势逐渐变缓，最终稳定在134.5 GPa附近.压入深度小于200 nm，改进Oliver-Pharr法的计算结果大于CSM的测量结果，压入深度大于200 nm，改进Oliver-Pharr法的计算结果与CSM的测量结果吻合程度高.

采用改进Oliver-Pharr法计算了PIN-PMN-PT铁电单晶的硬度，同时给出了CSM方法的测量结果，见图9.

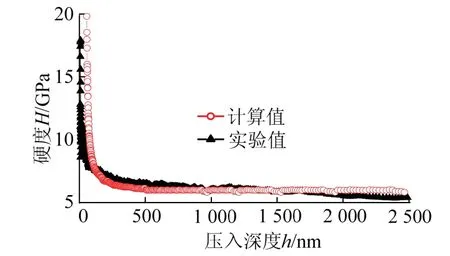
图9 硬度计算值与实验值对比 Fig.9 comparison of calculated and experimental hardness values

由图9可见，压入深度小于100 nm，PIN-PMN-PT铁电单晶的硬度随着压入深度的增加迅速减小；压入深度大于100 nm，硬度的减小趋势逐渐变缓，最终稳定在6.5 GPa附近.

压入深度小于100 nm，改进Oliver-Pharr法的计算结果大于CSM方法的测量结果，压入深度大于100 nm，改进Oliver-Pharr法的计算结果与CSM方法的测量结果吻合程度高.

4 结论

基于传统Oliver-Pharr法，提出一种根据实验数据计算接触刚度的改进Oliver-Pharr法.

（1）改进Oliver-Pharr法分析PIN-PMN-PT铁电单晶纳米压痕实验数据时，不需预先校正面积函数，就能得到与连续刚度测量实验结果相一致的结果，避免了在预先校正面积函数时的一些不确定因素的干扰.

（2）改进Oliver-Pharr法能连续计算得到接触刚度、杨氏和模量随任意压入深度的变化，且在稳定区间内与连续刚度测量法的实验结果相符.