脉冲参数对致密储层水力压裂起裂压力影响

董康兴，赵安楠，王素玲，赵 喆，孙 强

（1.东北石油大学 机械科学与工程学院，黑龙江 大庆 163318；2.中国石油勘探开发研究院，北京100083）

0 引言

由于致密储层具有低孔、低渗及埋藏深等特点，必须经过水力压裂才能形成高效开发.目前致密储层压裂改造主要借鉴页岩储层体积压裂技术，但相较于页岩储层，致密储层天然裂缝欠发育、体积压裂改造效果不佳，从而制约了致密储层勘探开发的效果[1-3].

脉动水力压裂技术是一种新兴的压裂技术，具有起裂压力低、压后裂缝扩展效果好等优点[4-6].付海峰[7]等通过脉冲致裂实验装置，考虑地应力场的影响，分析脉冲致裂的裂缝形态和延伸规律.李贤忠[8]采用正弦脉动波压裂改造煤层在煤矿瓦斯抽排应用中取得良好效果. 陈江湛[5]等、徐幼平[9]等、李全贵[10]等研究了煤层脉动水力压裂增透机制和型煤脉动参量的作用特性，阐明了脉动水力压裂相对于静压压裂在工业应用上的优势，脉动水力压裂能在较小注水压力下破坏煤岩，且频率越低，峰值压力越小，认为疲劳破坏是脉动水力压裂破岩的一种主要方式.谢正红[11]、WANG Wenchao[12]等均在现场试验中证明脉动水力压裂较常规水力压裂的压后流量明显增大.由此可见目前的研究大都集中在实验方面，而对于脉冲压裂裂缝的起裂机理研究较少.

为此，基于流固耦合理论，建立致密储层脉冲水力压裂损伤场计算模型，探讨脉冲幅值、波形等参数对损伤累积作用及起裂压力的影响规律.

1 脉冲水力压裂数学模型

1.1 损伤本构模型

采用应变等效假设计算含损伤的弹性模型[13].如果E为初始无损伤状态下材料的弹性模型，在单向拉压状态下胡克定律可表示为

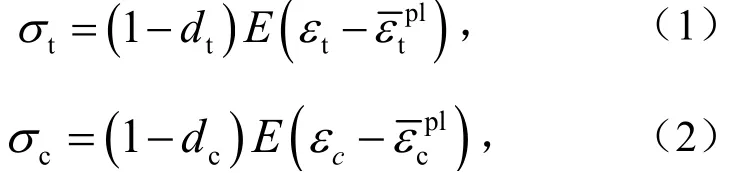
式中，σ为应力，Pa；ε为应变；为等效应变；d为损伤值.下标t表示拉伸相关的力学量；下标c表示压缩相关的力学量；上标pl表示为塑性.

材料损伤后弹性模量为

1.2 渗流模型

根据前期研究，压裂液在致密岩中渗流方程[14]可表达为

式中，α为Biot系数，α＜1；vε为体积应变；φ为孔 隙率；β1为流体体积模量，Pa；Ks为固体颗粒有效体积模量，Pa；k为渗透率，D；μ为流体动力黏度系数，N·s·m-2.；p为孔隙压力，MPa.

1.3 岩石损伤累积模型

致密岩在循环冲击作用下存在损伤累积效应，基于岩石循环冲击试验，可知岩石损伤累积演化模型[15]为

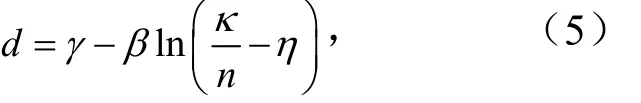
式中，γ、β、η为加载不同阶段累积速率因子，由试验测定；κ为轴向载荷，N；n为循环冲击次数.

2 计算模型

为模拟射孔周围岩体的力学行为，考虑边界效应，取厚度10 m，半径为3 m的岩体进行三维固结分析，岩体的三维力学模型和有限元模型见图1.

图1 地层岩体力学模型和有限元模型 Fig. 1 rock massmechanical model finite element model

在模型下表面施加Z方向的位移约束，四周边界施加位移约束，上表面施加上覆岩体压力PZ为-20 MPa，初始孔隙率为0.17，孔隙压力Ps为-18 MPa；X方向主应力最大，初始水平最大主应力σH为-35.9 MPa，水平最小主应力σH为-21.6 MPa，垂向应力σv为-45.6 MPa，四周表面为渗透边界，上下为不渗透表面.岩石初始弹性模量E取28× 109Pa，泊松比v取0.23，内摩擦角φ取22°，初始渗透率为0.1 mD，使用UMAT子程序定义材料的物理特性，并与USDFLD子程序结合，在每一步增量步结束后，对场变量进行更新.

该模型在文献[16]中利用解析解进行了正确性验证.采用常规压裂方式，注入压力为93.5 MPa时，射孔面最大损伤值达到1，代表岩石产生完全破坏，射孔面损伤云图见图2.

图2 射孔面损伤 Fig.2 perforation surface damage nephogram

3 数值结果与分析

经反复试算，注入压力低于64.5 MPa时，射孔面没有损伤，损伤值为0，大于64.5 MPa时，射孔面开始出现损伤，且注入压力越大损伤越大.当注入压力达到93.5 MPa时，损伤值为1，产生宏观裂缝.为分析不同频率对损伤的影响，分别计算压力为 65 MPa、70 MPa、75 MPa、80 MPa、85 MPa时，脉冲次数对损伤值的影响规律.

3.1 三角形脉冲压力影响规律

图3为三角形脉冲压力加载曲线，图4为加载过程中损伤值的变化规律.

图3 三角形脉冲压力加载 Fig.3 triangle pulse pressure loading

图4 加载过程中损伤值变化 Fig.4 damage change value during loading

由图3和图4可知，当脉冲压力以三角形形式变化时，随脉冲压力的施加，射孔面损伤值累积增加，直到损伤值为1，岩石破裂产生宏观裂缝.当脉冲压力在0～85 MPa变化，脉冲循环次数为2.62次时，射孔面最大损伤值达到1；而当脉冲压力在0～65 MPa变化，脉冲次数为13.7次时，射孔面最大损伤值达到1，表明脉冲压力幅值越大，裂缝起裂所需要的脉冲次数越少.

3.2 正弦形脉冲压力影响规律

图5为正弦形脉冲压力加载曲线，图6为加载过程中损伤值的变化规律.

图5 正弦形脉冲压力加载 Fig.5 sine pulse pressure loading

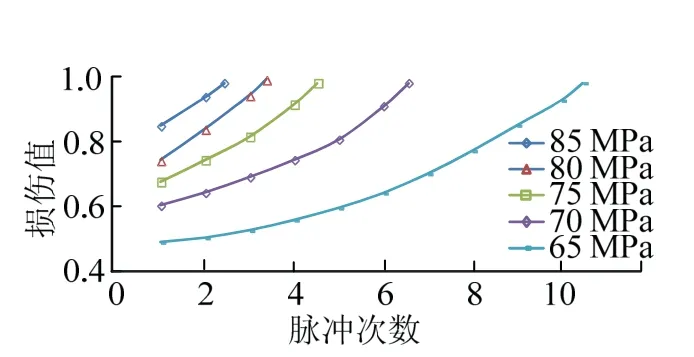
图6 加载过程中损伤值变化规律 Fig.6 damage change value during loading

由图5、图6可知，当脉冲压力以正弦形式变化时，随脉冲压力的施加，射孔面损伤值累积增加，直到损伤值为1，岩石破裂产生宏观裂缝.当脉冲压力在0～85 MPa变化，脉冲循环次数为2.22次时，射孔面最大损伤值为1；而当脉冲压力在0～65 MPa变化，脉冲次数为13.13次时，射孔面最大损伤值为1，表明脉冲压力幅值越大，裂缝起裂所需要的的脉冲次数越少.

3.3 矩形脉冲压力影响规律

图7为矩形脉冲压力加载曲线，图8为加载过程中的损伤值的变化规律.

图7 矩形脉冲压力加载 Fig.7 rectangular pulse pressure loading

图8 加载过程中损伤值变化规律 Fig.8 damage change value during loading

由图7、图8可知，当脉冲压力以矩形形式变化时，随脉冲压力的施加，射孔面损伤值累积增加，直到损伤值为1，岩石破裂产生宏观裂缝.当脉冲压力在0～85 MPa变化，脉冲循环次数为2.99次时，射孔面最大损伤值为1；而当脉冲压力在0～65 MPa变化，脉冲次数为15.51次时，射孔面最大损伤值为1，表明脉冲压力幅值越大，裂缝起裂所需要的的脉冲次数越少.

3.4 不同脉冲形式影响规律

图9为三角形、正弦形和矩形三种脉冲形式下，不同注入压力时脉冲次数对比.

由图9可以看出，随着射孔面注入压力的增加，损伤值达到1时所需脉冲次数逐渐减少；对于3种不同脉冲形式，相同注入压力时，正弦形脉冲所需循环次数最少，其次为三角形脉冲和矩形脉冲.

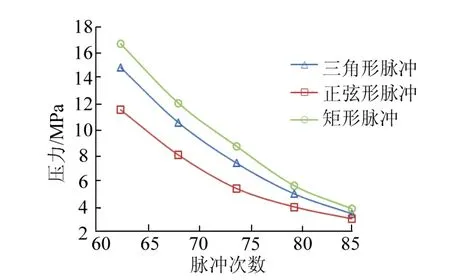
图9 不同脉冲形式裂缝起裂所需加载次数对比 Fig.9 comparison of loading times for crack initiation in different pulse forms

对于3种脉冲，在增加脉冲循环次数的情况下，注入压力最大值为65 MPa时，射孔面损伤值均能达到1，达到起裂条件.因此，在脉冲压裂条件下致密储层的起裂压力由注入压裂时的93.5 MPa下降至65 MPa，下降幅度达30.48%.

4 结论

（1）基于岩石力学、渗流力学理论建立了脉冲压力下致密储层脉冲水力压裂裂缝起裂计算模型，使用UMAT定义材料的物理特性，与USDFLD子程序结合，对材料属性进行实时更新，模拟脉冲压力对材料性能的影响.

（2）随着脉冲次数的增加，射孔面损伤值逐渐累积；脉冲幅值越大，损伤越大，达到起裂条件所需要的脉冲循环次数越少；注入压力相同时，正弦形脉冲所需循环次数最少，其次为三角形脉冲和矩形脉冲.

（3）基于损伤累积效应，通过降低脉冲幅值，多次循环累积致裂降低起裂压力，特定情况下脉冲水力压裂能降低起裂压力达30.48%.