端部效应对砂岩单轴压缩蠕变特性影响

苏荣华，马志远，薛佳琪

（辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000）

0 引言

在岩石单轴压缩试验中，试件的端部与试验仪器接触所产生的端部效应使仪器与砂岩接触面在加载过程中的变形比例不一致，因此限制试样的端部变形会影响试件在加载过程中的应力应变分布.国内外学者均对单轴压缩试验所产生的端部效应进行过探究.侯宏涛[1]等通过放置不同垫片的方式进行岩石单轴压缩试验，得出不同端部摩擦下的垂直应力分布规律.薛俊华[2]等设置岩石与装置的多种接触方式，进行岩石单轴压缩实验，得到端部效应对岩石力学特征的影响.王学滨[3]等进行考虑端部效应的数值模拟，并分析端部效应对模型剪切带、速度场等的影响.梁正召[4]等对不同接触面的岩石进行考虑端部效应的数值模拟.麦戈[5]等对不同摩擦系数下的岩石试件进行单轴压缩数值模拟.郭金宝[6]等通过压缩试验得出不同尺寸下单轴强度随端部摩擦因子增加而增大的结论.

在蠕变试验方面，赵宝云[7]等对红砂岩进行循环载荷蠕变试验，研究循环次数与红砂岩蠕变特征之间的关系.王俊光[8]等研究了不同扰动幅值和频率对泥岩蠕变及断口细观特征的影响.史宝宁[9]分析了不同含水率不同荷载等级下粉砂岩的蠕变变化规律. MANSOURI H[10]等研究蠕变试验引起的盐岩微观结构演化如何影响应力应变行为.JIANG Annan[11]等运用一种化学和应力耦合作用下的蠕变设备，在不同PH环境下对岩石进行单轴压缩蠕变试验.

在数值模拟方面，学者对描述加速蠕变阶段的方法做了大量改进，建立自定义本构模型，对宏观蠕变行为进行预测.高文华[12]等基于FLAC3D软件，建立粉砂岩单轴压缩蠕变数值试验模型，探讨粉砂岩在各应力水平下蠕变特性.贺其[13]基于红砂岩蠕变试验结果，针对加卸载条件进行单轴蠕变模拟研究. AZIZNEJAD S[14]等建立合粒子模型以模拟完整岩石的静态和动态特性，通过数值模拟确定刚性射弹粒子对节理岩体样品造成的冲击损伤.WANG Yujie[15]等将VIB扩展用于建立黏弹性模型，并引入混合超弹性-开尔文键有效地模拟了蠕变过程.

综上，针对岩石单轴压缩试验中存在端部效应进行了大量研究，而较少考虑端部效应对岩石蠕变试验结果的影响.为此，利用基于课题组自主研制的蠕变试验装置，探讨砂岩试件在单轴压缩下的蠕变特性.基于试验结果设计有、无端部效应两种模拟方案，选用Cvisc蠕变模型，利用FLAC3D软件中fish语言编程进行数值模拟，分析有无端部效应时模型应力、应变及塑性区分布特征.

1 砂岩单轴压缩蠕变试验

1.1 岩样制备及试验设备

试验所用砂岩选自同一岩块，通过室内钻取加工为Φ50 mm×100 mm的标准圆柱体试件，通过声波测速剔除离散性较大的试件，把均匀性良好的试件分为2组并进行编号，第1组进行单轴压缩试验，获取试件强度等基本物理力学参数作为蠕变试验加载等级的依据，第2组进行单轴压缩蠕变试验.试验所用试件的基本物理力学参数平均值见表1.

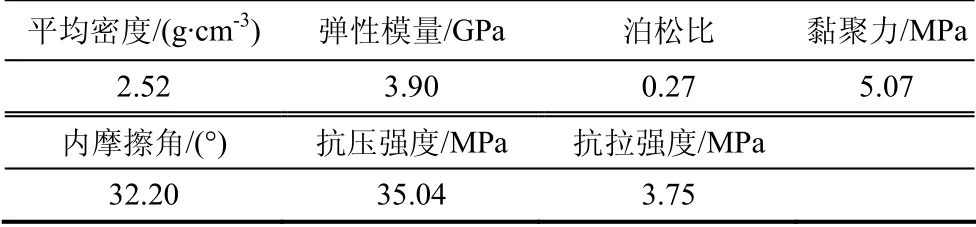
表1 砂岩基本物理力学参数 Tab.1 basic physical and mechanical parameters of sandstone

试验采用自主研制的单轴压缩蠕变试验装置，该装置的原理图见图1.试验运用双杠杆原理，将加载筐砝码重力放大后垂直施加在试件上，采用千分表测量圆柱体砂岩试件的轴向位移.

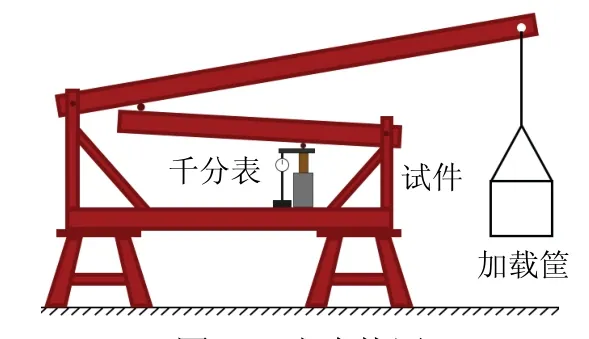
图1 试验装置 Fig. 1 test device

1.2 试验过程

（1）将砂岩试件放入试验装置加载平台的中间位置，避免偏心力产生，两端安放粗糙承压板，将试件和承压板放置好后安装千分表.

（2）量取加载所需质量M，缓慢放入加载筐，避免冲击加载.

（3）记录加载时间和砂岩试件轴向位移，至岩石试件破坏，记录破坏形式、表面裂隙发育情况等.

1.3 试验结果分析

图2为单轴压缩蠕变应变.

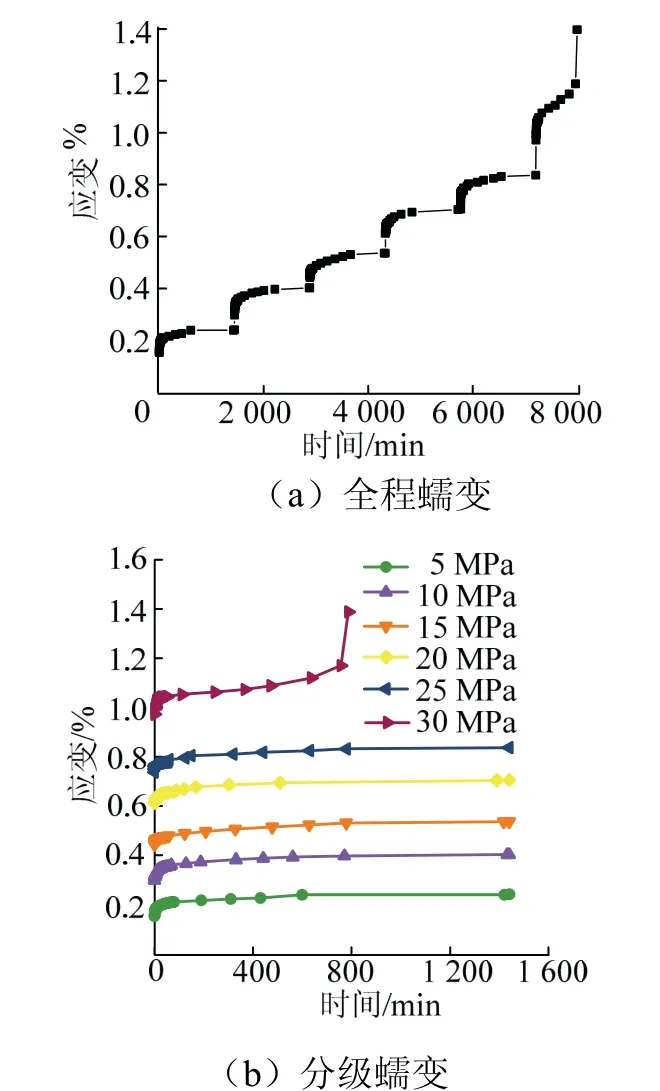
图2 砂岩单轴压缩蠕变 Fig.2 uniaxial compression creep of sandstone

加载等级低于15 MPa时，砂岩试件应变速度逐渐下降并进入了稳定蠕变阶段，300 min内逐渐稳定.加载等级为15 MPa时，砂岩试件在540 min内进入稳定阶段.加载等级为30 MPa时，出现等速蠕变阶段，经历较短时间后进入加速蠕变阶段，砂岩试件发生破坏.

图3为单轴压缩蠕变试验砂岩发生的破坏形态.

图3 砂岩试件破坏形态 Fig.3 sandstone specimen failure mode

从图3中可以发现，砂岩破坏前两端出现细小粉末脱落，试件外表面细小剥落，裂隙条数发展至3条后发生破坏，破坏时以剪切破坏为主，发生的位置在中上部，破坏斜面比较完整；25～30 MPa的轴向载荷使得砂岩试件内部的裂隙加速发育，同时加速外表面张力裂隙的形成，达到砂岩的破坏阈值后，裂隙贯通，加速破坏.

2 砂岩蠕变端部效应分析

由上述实验结果发现砂岩蠕变经历弹性、塑性及黏性阶段，将岩石材料视为均匀、连续的各向同性材料，3阶段分别服从广义胡克定律、理想弹塑性材料的增量方程及元件模型，对3个阶段进行分析.

弹性阶段服从广义胡克定律.

当试验设备与砂岩试件接触面光滑，砂岩试件端面自由，则

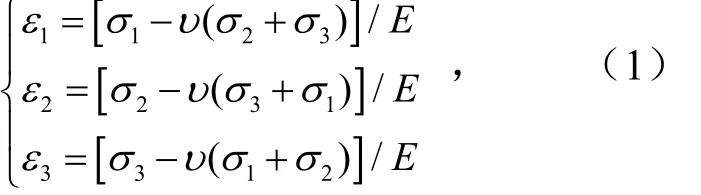
式中，ε1为轴向应变；ε2、ε3为水平方向应变；σ1为轴向应力，MPa；σ2、σ3水平方向应力，MPa；v为泊松比；E为弹性模量，MPa.

当端面受约束时，端面微元体无水平方向应变，即σ2=σ3=0，此时

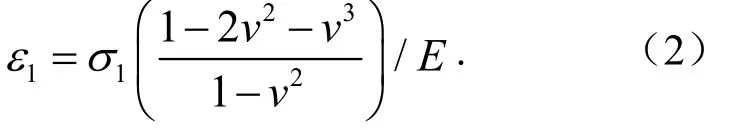
由式（1）、式（2）可知，控制端面可增加水平方向的σ2和σ3.

塑性阶段的塑性本构方程为

式中，εii为应变球张量；σii为应力球张量；eij为应变偏量；sij为应力偏量；εi为应变强度；σi为应力强度，MPa.

黏性阶段Burgers模型本构方程为

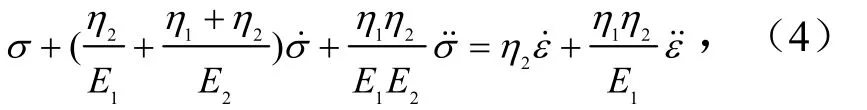
式中，E1、E2分别为瞬时弹性模量、黏性模量，MPa；σ、σ分别为应力对时间t的一阶导数、二阶导数；ε、ε分别为应变对时间t的一阶导数、二阶导数；η1、η2为黏滞系数.

在恒定应力 作用下，其蠕变方程为

式中，k1和k2为Maxwell体和Kelvin体的弹性常数. 通过弹性、塑性及黏性3个阶段分析可知，ε1主要受σ1的影响，主要研究在单轴压缩蠕变实验中端部效应对砂岩试件变形及破坏的影响.

3 砂岩蠕变端部效应模拟分析

3.1 蠕变模型建立

为探究端部效应对砂岩单轴压缩蠕变试验结果的影响，采用FLAC3D软件fish语言编程进行模拟分析.模型采用试验尺寸相同的圆柱模型，共划分为1 500个单元1 616个节点.由单轴压缩蠕变试验特点选用Cvisc模型，该模型为基于Mohr-Coulomb准则的Burgers模型，见图4.

图4 Cvisc模型 Fig.4 Cvisc model

当σ0＜σf＜σs时，只发生瞬时弹性应变.（σf、σs分别为起始蠕变应力和屈服应力，MPa.）

当σf＜σ0＜σs时，模型简化为伯格斯模型，其蠕变方程为，

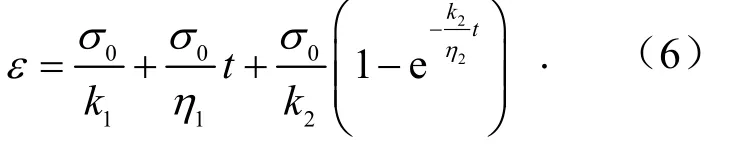
当σf＜σs＜σ0时，模型的蠕变方程为

式中，εp为塑性应变；σ0为参考应力，MPa.

Mohr-Coulomb准则为

式（8）～式（10）中，c为材料黏聚力，kPa；φ为摩擦角，°；σt为抗拉强度，MPa.

数值模拟选用的砂岩参数全部由基础物理力学试验所得，其中体积模量、剪切模量等由已知参数换算得出.考虑到试验过程中砂岩试件会受端部效应的影响，设计2种不同的模拟方案.

（1）模型1：只受y=0的轴向约束，试件端面有膨胀.

（2）模型2：受y=0轴向约束，约束水平方向的位移，试件端部无膨胀.

3.2 模拟结果分析

（1）轴向应力对比

图5给出2种模拟方案下最后一个加载等级时模型的轴向应力分布情况.

图5 最终破坏的轴向应力 Fig. 5 axial stress cloud diagram of final failure

由图5（a）、图5（b）可见，由于静载蠕变加载沿y轴向下，模型受力呈现“漏斗形”式分布.从图5（b）可以看出模型底部中心受力最大.随着加载水平逐渐变大，最大轴向应力逐渐变大.加载过程中，加载瞬间的模型应力云图变化最明显，加载停止后云图形状颜色基本没有变化，只有应力逐渐增大；第7级加载后，模型最上端应力达到最大值，云图发生改变，模型破坏.

由图5（c）、图5（d）可见，由于控制端部导致模型上部周围轴向应力随加载等级升高逐渐变大，模型上部中心和底部应力最大；由图5（d）可见，控制端部会使应力集中在上端部中心，到第6级模型中心出现新的应力集中部分，模型在第6级发生破坏；与未控制端部相比，模型内部应力分布不均匀，因此破坏时间早于有端部效应的模型.

（2）径向应力对比

最终破坏的径向应力见图6.由图6（a）、图6（b）可见，模型1破坏前径向应力以拉应力为主，只有底部中心处受压应力，上部呈现“漏斗形”分布；破坏时，模型下部受拉应力，上部中心受压应力，从截面图可以发现模型中心出现应力集中，可以推断试件内部发生破坏；由图6（b）还可见，应力分布呈斜向角度在45°左右；模型径向应力图变化规律同轴向，加载瞬间云图变化较大，稳定蠕变时径向应力变化不大.

分析图6（c）、图6（d），在对控制端部位移后，模型2上下端部受径向压应力最大，模型其余部分受拉应力，侧向不同位置的应力值都有变化，模型内部受拉应力大于外部；随加载等级升高，拉应力逐渐减小，破坏点出现应力集中；破坏前后上端部径向压应力呈一定角度的斜向下减小，下断面径向压应力向上减小，与有端部效应的应力场分布完全不同.

图6 最终破坏的径向应力 Fig.6 radial stress cloud diagram of final failure

综上所述，模型2由于控制端部膨胀导致的模型内部应力分布不均匀，模型上半部分产生更大的剪切变形，比模型1更快进入加速蠕变阶段.

（3） 轴向位移对比

图7为观测点轴向位移.由图7可见，每级加载瞬间模型轴向位移产生突变，然后趋于稳定；与未控制端部的模型相比，控制端部的模型加载等级较高；最后一级加载出现在加速蠕变阶段，在逐级加载的应力作用下，数值计算结果经换算得到的观测点轴向位移时程曲线与试验结果趋势相近，这表明数值模拟结果理想.

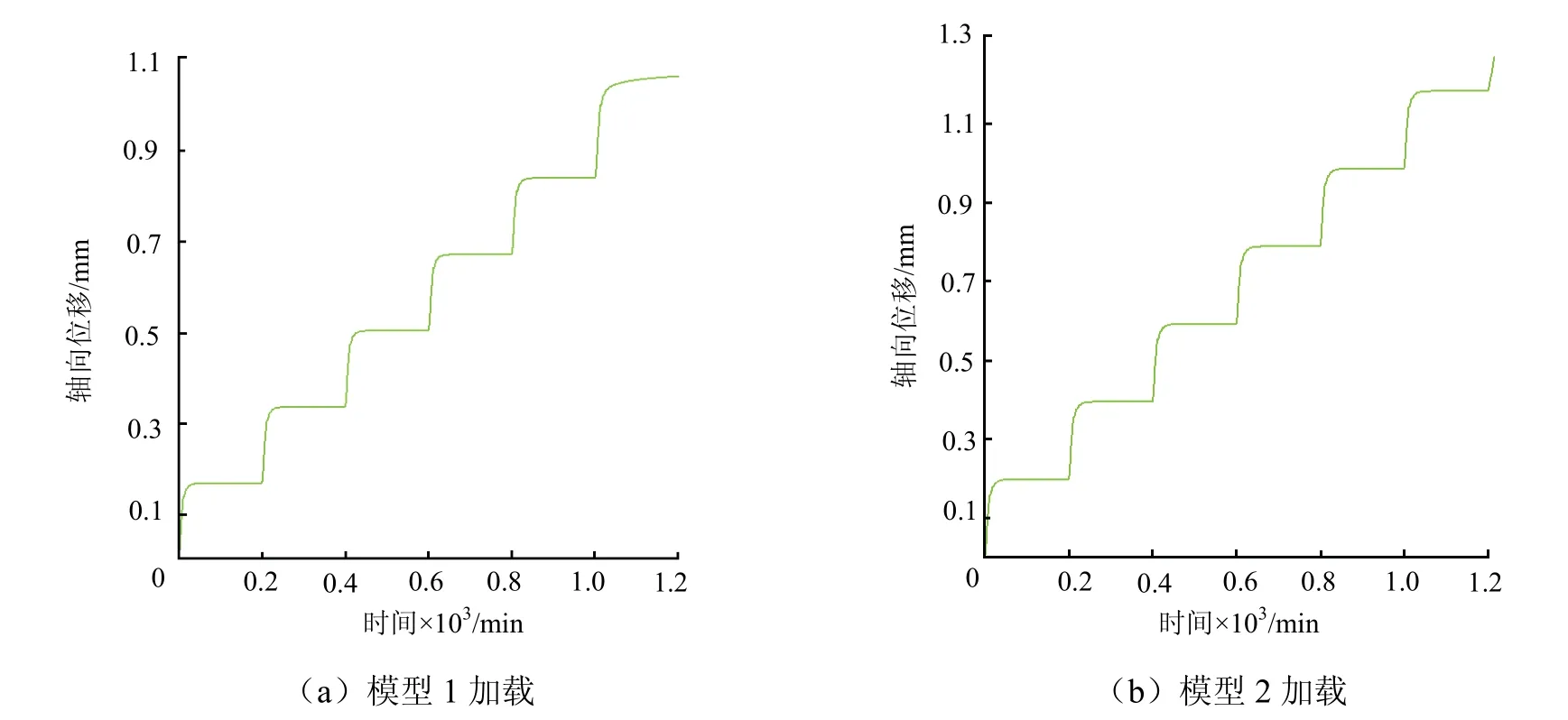
图7 试样轴向位移 Fig.7 axial displacement of the specimen

图8给出最后一个加载等级的轴向位移云图.

图8 最终破坏的轴向位移 Fig.8 axial displacement cloud diagram of the final failure

通过观察图8（a）、图8（b）可见，砂岩顶部轴向位移最大，向下均匀减小，整体与试验结果较符合；对比分析发现模型上部外圈轴向位移最大.

通过观察图8（c）、图8（d）可见，控制端部，模型两端轴向位移最大，远离端部逐渐减小.随着载荷提高，端部轴向位移越来越大.对比之前未控制断面的截面轴向位移图可以发现，控制端部使模型内部轴向位移分布不均匀，由直线变成一条凹形曲线，说明上半部分中间处轴向位移最大，是发生破坏的位置，而下端部附近位移由平稳直线变成波浪线，可以推断模型内部轴向变形十分不均匀.

（4）塑性区对比

图9为2种方案下砂岩破坏时塑性区分布情况.

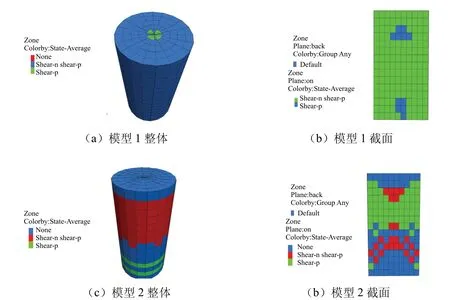
图9 最终破坏的塑性区 Fig.9 cloud map of the plastic zone of the final failure

观察图9中未控制端部的模型1外部侧面塑性区域可以发现，整个模型周围处于剪切屈服状态，蓝色单元表示该区域曾经发生剪切屈服且现在仍然处于剪切屈服中，绿色区域表示曾经发生剪切屈服；模型内部绿色区域表示曾经发生剪切屈服且现在仍然处于剪切屈服中，蓝色区域表示曾经发生剪切屈服；这些单元的屈服状态和形状显示出模型的破坏情况.

同理可看出控制端部的模型呈明显剪切屈服状态，从模型塑性区域推断其沿45°发生破坏，可以认为45°方向应力最大，因此发生破坏.

模型不同位置的轴向应力、径向应力、轴向位移和径向位移都不同，侧向和内部都有很大区别，只受轴向约束和控制端部膨胀的应力变化趋势相差很大；是否控制端部对塑性区域有影响，二者破坏形式不同；只受轴向约束的砂岩蠕变数值模拟破坏载荷大于实际试验结果，控制端部的砂岩数值模拟破坏载荷更接近实际试验结果.

4 结论

（1）针对砂岩试件进行考虑端部效应的单轴蠕变试验，发现砂岩蠕变仍包括3个阶段，其破坏形式主要为剪切破坏，基于蠕变时程曲线选定Cvisc蠕变模型并确定其蠕变参数.

（2）考虑砂岩试件端部效应的影响进行蠕变数值模拟，未控制端部时，模型的轴向应力、径向应力分布在上端呈“漏斗形”分布；控制端部时，模型的轴向应力、径向应力分布在中部出现明显应力集中区.

（3）控制端部时，模型变形随着与端面距离的增大而减小，加载等级提高，塑性区形成剪切带.控制端部后的模拟结果与实验结果相近.