露天煤矿爆破振动速度计算公式研究

代树红，安志奎，王晓晨,2，韩荣军

（1. 辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000；2. 湖北汽车工业学院 汽车工程学院，湖北 十堰 442000）

0 引言

爆破是露天煤矿开采的主要施工手段，频繁爆破作业引起的振动威胁着露天煤矿生产安全和周围建筑物的安全.基于露天煤矿爆破作业方式和矿区地形地貌的特殊性，确定合理的露天煤矿爆破振动速度计算式，对优化露天煤矿爆破作业方式和评估矿区附近建筑物安全性具有重大意义.

露天煤矿爆破地震波在受边坡及深凹地形影响的条件下，采用萨道夫斯基公式计算爆破振动速度的误差较大，因为没有充分考虑高程因素的影响.近年来，国内外学者对露天煤矿爆破地震波传递与衰减规律进行了大量研究.蒋楠[1]等基于量纲分析方法改进了考虑高程影响因素的爆破振动速度公式.谭文辉[2]等通过现场试验研究高程差变化对振动公式的场地系数K和振动衰减指数α的影响规律，得出不同岩性时K和α随高程差的变化规律.谢承煜[3]等通过对露天煤矿爆破振动进行监测，得出爆破振动波传播衰减规律.李廷春[4]等从爆破地震效应分析入手，对爆破地震波在岩石高边坡介质中的传播机理和高陡边坡控爆减震的基本原理进行了研究.张小军[5]等研究表明高程对爆破振动同时存在放大效应与衰减效应，且以衰减效应为主，放大效应为辅.张伟康[6]等通过量纲分析法推导了反映高程放大效应的爆破振动式，公式计算误差小于传统萨道夫斯基式.张声辉[7]等结合露天矿爆破振动监测实例，利用小波变换对不同高程的爆破振动信号在各频带间的能量分布特征进行研究.代树红[8]等采用回归分析方法对露天矿相关爆破振动公式进行分析，得出广义公式和考虑高程影响的振动速度经验公式的计算误差低于萨道夫斯基公式.以上成果促进了爆破振动速度计算公式研究，但针对露天煤矿爆破振动速度计算公式研究较少，仍没有得到适用于露天煤矿爆破振动速度计算公式的方法.

通过现场试验，测定五虎山煤矿主扇区的爆破振动信号，研究邻近露天煤矿爆源的高程对爆破振动速度的影响；通过量纲分析方法，推导出适用于露天煤矿的爆破振动速度计算公式，结合现场测试数据，分析了爆破振动计算公式计算结果的准确性.

1 爆破振动现场监测

1.1 工程背景

在五虎山煤矿井田附近建有乌海市建安煤矿和乌海市华银煤矿两家露天矿.五虎山煤矿九层回风井、十二层回风井以及瓦斯电站靠近建安露天矿的南端帮边坡和华银露天矿的北端帮边坡，其中九层风井主扇距建安露天矿南端帮约70 m，十二层风井主扇距华银露天矿北端帮约60 m.两家露天煤矿的频繁爆破作业使九层和十二层回风井出现严重裂缝，瓦斯电站墙体出现开裂.为确保九层和十二层回风井稳定以及五虎山瓦斯电站和人员的安全，对该区域的爆破振动速度和结构的动力学响应进行了现场监测.

1.2 爆破振动

爆破监测区域为五虎山九层回风井和十二层回风井，共设置8个测点，进行爆破监测的五虎山主扇区域高程为1 250 m，测点及监测区域见图1.爆破炸药种类为乳化炸药，爆破方式为裸露爆破法，现场测试爆破数据见表1.现场测试使用M20爆破测振仪采集爆破地震波参数，采用中国地震局工程力学研究所研制的891系列拾振仪和测振系统，对建筑物进行振动监测，现场监测情况见图2.仪器能够覆盖爆破振动的频率范围，动态监测爆破振动信号.

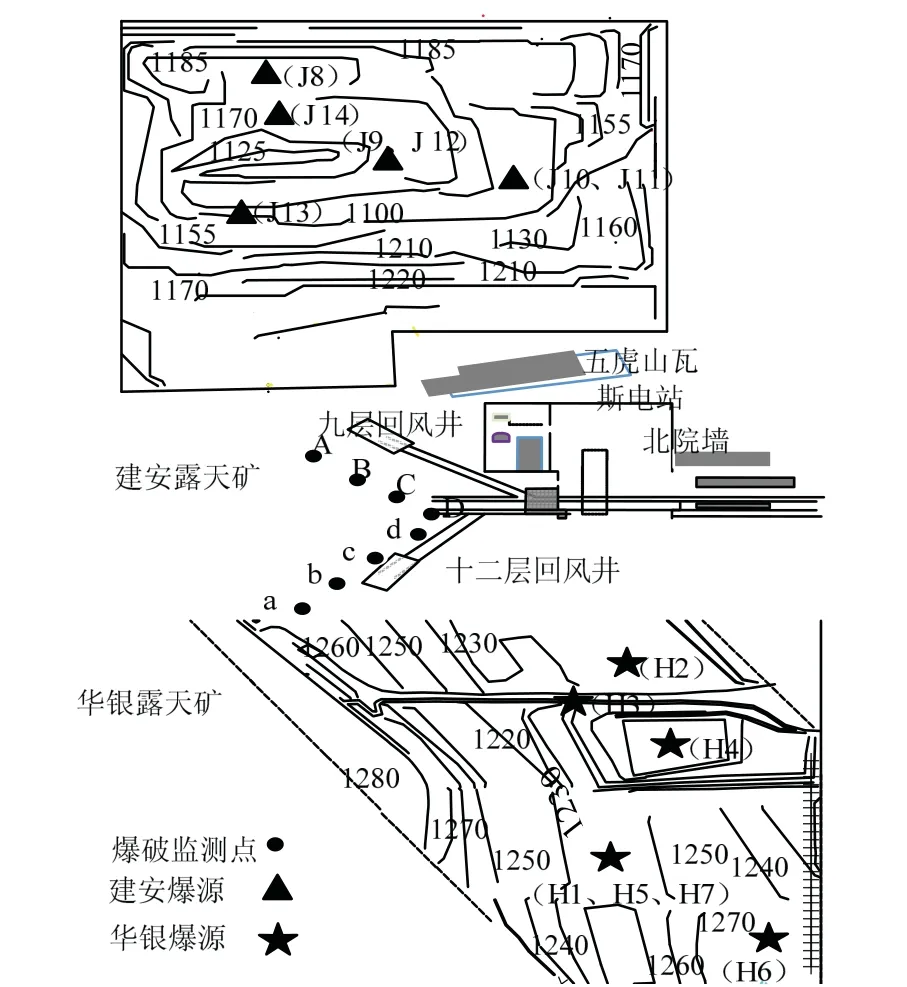
图1 监测点示意 Fig.1 schematic of testing points

表1 爆破监测数据 Tab.1 blasting data

图2 现场测试示意 Fig.2 schematic of field test

2 露天煤矿爆破结果分析

2.1 经验公式分析结果

根据《爆破安全规程》（GB6722-2014）[9]可知，国内工程实际中普遍采用萨道夫斯基公式计算爆破振动速度，计算式为

式中，R为测点至起爆中心的水平距离，m；Q为爆破时最大段炸药质量，kg；V为爆破时地表质点振动速度，cm/s；K为场地系数；α为爆破振动衰减指数.

《水工建筑物岩石基础开挖工程施工技术规范》（DT/L5389-2007）[10]和相关学者考虑高程对振动速度的影响，提出爆破振动速度公式为

式中，H为起爆点至测点的高程差，m；β为与高程有关的影响系数.

通过表1的炸药质量、振动速度、水平距离和高程等数据对式（1）和式（2）进行回归分析，得出场地系数K和衰减指数α，见表2和表3.

表2 萨道夫斯基公式系数 Tab.2 coefficients of Sadovsky formula

表3 考虑高程的萨道夫斯基公式系数 Tab.3 coefficients of Sadovsky formula considering elevation

将表2中的系数代入式（1），得到华银露天矿和建安露天矿的萨道夫斯基公式分别为

式中，V1、V2分别为华银与建安露天矿的爆破振动速度，cm/s.

将表3中的系数代入式（2），华银露天矿和建安露天矿考虑高程的萨道夫斯基公式分别为

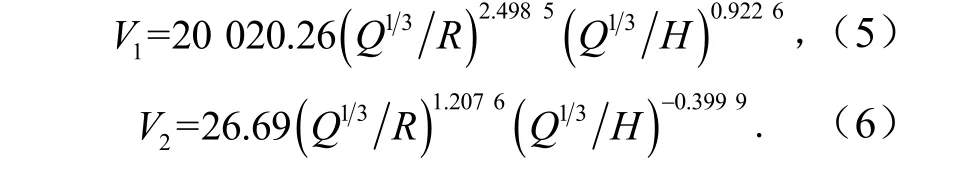
选表1中的爆破数据分别代入传统萨道夫斯基公式和考虑高程的萨道夫斯基公式，计算爆破振动速度，与现场实测的振动速度进行对比，得出不同爆破振动速度公式的计算结果和相对误差，见表4.

表4 振动速度的计算误差分析 Tab.4 analysis of error analysis of vibration velocity

由表4中的数据可见，当爆源高于被测点时，萨道夫斯基公式计算得到的振动速度高于实测振动速度；当爆源低于被测点时，随着高程差变大，萨道夫斯基公式计算得到的振动速度从高于实测振动速度下降为低于实测振动速度.爆破地震波传播到露天矿的坡面时，在坡面上传统萨道夫斯基公式未考虑高程差对于地震波的放大作用，不适用于露天煤矿爆破振动速度的计算.考虑高程的萨道夫斯基公式的计算结果随着高程差变大，计算振动速度的相对误差随之增加.这是由于露天煤矿特殊的场地因素影响，随着高程差变大，爆破地震波沿着露天矿坡面传播的路程也随之增大，当地震波衰减效应强于坡面放大作用时，考虑高程的萨道夫斯基公式会出现较大误差.因此，考虑高程的萨道夫斯基公式也不适用于露天煤矿爆破振动速度的计算.

2.2 基于量纲分析的振动速度公式

爆破地震波在露天煤矿的传递分为沿边坡与矿坑直线传递2种方式，爆破地震波传递至坡面时将发生反射.当露天煤矿爆源深度较小时，入射波和反射波进行叠加作用，边坡对于爆破振动的传递具有放大作用；当露天煤矿爆源深度较大时，需考虑爆破振动波沿坡面传递过程中的衰减效应，传统经验公式计算爆破振动速度存在较大误差.考虑高程效应的萨道夫斯基公式，仅将高程差与爆心距作为2种独立的影响因素，未考虑露天煤矿爆破深度与水平距离之间的比值.

1.1 一般资料 选取自2010—2017年北部战区总医院行原位心脏移植术的34例患者为研究对象。按心脏移植术后是否出现过排斥反应分为排斥组(n=12)及无排斥组(n=22)。排斥组中，男性10例，女性2例；年龄45～63岁，平均年龄(56±6)岁。无排斥组中，男性16例，女性6例；年龄30～66岁，平均年龄(50±10)岁。两组患者一般资料比较，差异无统计学意义(P>0.05)，具有可比性。本研究经医院伦理委员会批准，患者均签署知情同意书。

为研究适应于露天煤矿的爆破振动速度计算公式，从量纲角度对露天煤矿爆破振动公式进行分析.根据以往研究[11-12]，爆破过程中涉及到的物理参数见表5.

表5 影响爆破振动传播的物理参数 Tab.5 physical coefficients affecting the propagation of blasting vibration

根据量纲齐次原则，因π1为无量纲量，则H与Qαrβtγ量纲相同，有

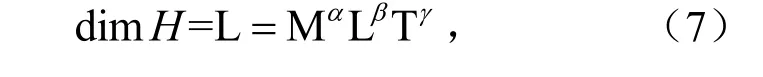
可知， 0=α， 1=β， 0=γ，所以有

对于π2有

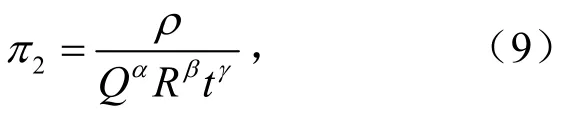
根据量纲齐次原则，因π2为无量纲量，则ρ与QRtαβγ量纲相同，有

可知， 1=α， 3=β-，=0γ，所以有

同理可知

由量纲和谐性原理，在力学上任何有物理意义的方程或关系式，每一项的量纲必定相同，对无量纲量 3π和 4π进行运算，设其结果为

对无量纲量π1、π2进行运算，设其结果为

由量纲原理可知，π8和π9均为无量纲量，振动波速的c、介质密度的ρ均视为常量.因此，振动速度V可表示为与自变量H/R和Q1/3/R相关的函数，对比萨道夫斯基公式并考虑高程的放大效应，振动速度V的对数函数式可取为

则有

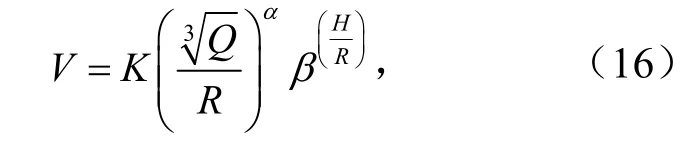
当高程差H等于0时，基于量纲分析的式（16）自动退化为萨道夫斯基公式，解决了式（2）和类似振动速度计算公式计算结果畸变问题；当高程差H大于0时，式（16）反映高程差正值时振动速度的放大效应；当高程差H小于0时，式（16）反映高程差负值时振动速度的缩减效应.基于量纲分析的振动速度式（16）通过H/R值量化爆破地震波在露天煤矿沿边坡与矿坑传递的缩放值，确定爆破振动速度在露天煤矿特殊的地形地貌条件下传递的缩放特征及规律.

3 测试验证

分别将表1中的华银露天矿爆破数据和建安露天矿爆破数据代入式（15）进行回归分析，分别得出华银和建安露天矿对应的回归方程为

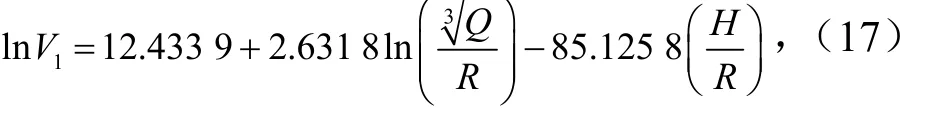
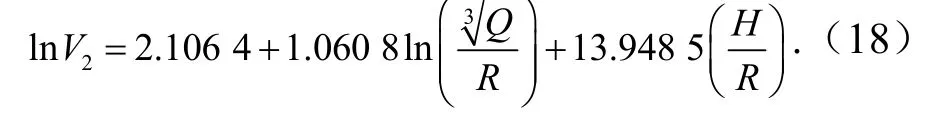
将表1数据代入式（17）和式（18），对计算振动速度与现场实测振动速度进行对比，误差分析结果见表6.

表6 振动速度的误差分析 Tab.6 physical coefficients affecting the propagation of blasting vibration

结合表4和表6的数据可知，传统萨道夫斯基公式计算爆破振动速度的相对误差最大为138.46%，平均误差为74.74%；考虑高程的萨道夫斯基公式计算爆破振动速度的相对误差最大为292.78%，平均误差为81.65%.基于式（16）计算爆破振动速度的相对误差最大为61.31%，平均误差为32.85%.基于量纲分析的振动速度公式的计算精度明显高于传统萨道夫斯基公式和考虑高程的萨道夫斯基公式的计算精度，减小了露天煤矿爆破振动速度的计算误差.

4 结论

（1）当爆源高于被测点时，传统萨道夫斯基公式计算得到的振动速度大于实测振动速度；当爆源低于被测点时，计算得到的振动速度低于实测振动速度.考虑高程的萨道夫斯基公式的振动速度计算相对误差，随着高程差增大而增加.传统的萨道夫斯基公式不适用于露天煤矿爆破振动速度的计算.

（2）基于量纲分析理论，推导出表述露天煤矿爆破振动缩放效应的振动速度计算公式.当高程差 0H=时，基于量纲分析的振动速度公式自动退化为萨道夫斯基公式，避免了其他相关振动速度计算公式计算结果出现畸变的问题.

（3）在露天煤矿特殊的地形地貌条件下，传统萨道夫斯基公式和考虑高程的萨道夫斯基公式计算爆破振动速度的平均误差分别为74.74%和81.65%；基于量纲分析的振动速度公式的平均计算误差为32.85%，有效提高了露天煤矿爆破振动速度的计算精度.