高速铁路无砟轨道不平顺分形特征分析

李再帏， 吴鹏飞， 刘晓舟， 何越磊

(1. 上海工程技术大学 城市轨道交通学院，上海 201620; 2. 深圳技术大学 城市交通与物流学院，深圳 518118)

无砟轨道作为高速列车行车的基础结构，其服役状态直接影响高速列车运行的平稳性和安全性[1]。轨道不平顺作为轨道服役状态劣化的直接表征，一直是铁路管理部门养护维修作业的重点内容[2]。通过持续、高效、精准地对高速铁路无砟轨道进行维修保养，目前我国高速铁路轨道不平顺时域幅值超限问题极少，轨道质量指数((track quality index, TQI)保持着优秀状态。以华东区某300 km/h的高速铁路为例，2020年5月动检车单次检查轨道不平顺仅存在41次I级超限，病害里程占比为0.003 4%。但同样值得注意的是，由于该线路采用的CRTS II型板式无砟轨道结构，线路维修部门通过线路巡检，发现存在连续胀板病害的里程为1.45 km，病害里程占比为0.57%；而从胀板区段轨道不平顺的时域波形来看，呈现明显的温度效应，导致了胀板结构性病害，但胀板区段的时域幅值均满足现行幅值管理中优良标准[3]。这说明现有无砟轨道不平顺的管理存在一定的局限性，需要进一步地分析轨道不平顺时空分布特征，实现轨道结构服役状态精准而有效地管理。

轨道不平顺的检测一般是通过轨道检测车动态检测来实现的[4]，对所获取检测值的评价管理，世界各国多采用区段均方值或局部偏差值等时域幅值方法，但各国的相应计算公式和管理长度略有不同，如中国和美国铁路的TQI指数[5]、印度铁路的TGI指数[6]、波兰铁路的J指数[7]、瑞典铁路的Q指数[8]以及欧盟的SD指标[9]等。此外，由于高速列车运行中轨道不平顺波长的作用显著，除了利用常规的轨道不平顺谱评价方法[10]外，研究人员从频域和时频域的角度，结合轮轨动力学作用，讨论了轨道质量的评价方法，如文献[11]基于轮轨系统动力响应采用带通滤波方法建立了轨道不平顺敏感波长计权评价指标；文献[12]利用局部波动的多尺度标准差卷积变换模型提出了轨道局部波动指数；文献[13]利用经验模态分解法得到轨道不平顺在各个波段的固有模态函数，提出轨道质量能量指标；文献[14]则利用集合经验模态分解对波长能量进行量化；文献[15]基于神经网络方法对车辆振动进行映射，通过振动影响来实现轨道质量的评价；文献[16]利用分形维数讨论了普速有砟线路轨道不平顺在两个波长区间的分形特征，文献[17]则在其基础上，结合欧盟标准，进一步地讨论提速有砟线路在3个波长区间的分形特征。这些研究从多个层次和维度对轨道质量进行评价，具有十分积极的现实意义；但同样值得注意的是，在各运行速度下不同车辆类型对轨道不平顺波长的敏感度有显著差异性，难以用统一波长区段进行定义和度量，虽然既有研究讨论了有砟线路轨道不平顺的分形特征，但该研究分形维数计算方法(尺码法)的本质还是基于车辆振动响应的敏感波长，这无疑使得分形计算具有一定的不稳定性，无法建立统一的度量尺度。所以，需要进一步地挖掘轨道几何不平顺细观特征，探究其内在反映的客观规律，从而实现轨道质量的有效评价。

基于此，本研究从高速铁路无砟轨道不平顺的分形特征出发，通过若干分形维数计算方法的比选，确定无砟轨道不平顺的分形描述方法；分析典型高速铁路无砟线路的累计检测数据，研究无砟轨道不平顺分形维数的分布特征，讨论无砟轨道不平顺的分形维数评价指标的可行性与合理性。

1 轨道不平顺分形特征与分形维数计算方法

1.1 轨道不平顺的分形特征

分形是指具有自相似性的一类图形的总称[18]。自相似性和标度不变性是分形的基本特征[19]。自相似性是指分形的局部与整体存在某种相似性，这种自相似可以是精确的自相似，也可以是近似或统计意义上的自相似。标度不变性是指对分形进行尺度变换，其分形特性保持不变的一种性质。因此，要实现轨道不平顺分形特征的有效表达，首先需要确定其是否具有自相似性和标度不变性。

一般而言，轨道不平顺可以视为是由不同幅值、频率、相角的简谐波叠加而成的复杂随机波，其局部与整体天然存在一定的相似性。由中国高速铁路无砟轨道谱[20]可知，在一定范围尺度(空间频率)与测度(功率谱密度(power spectral density，PSD))具有明显的线性关系，即轨道不平顺具有标度不变性，如图1所示。

图1 高速铁路无砟轨道不平顺谱

根据标度不变性的定义，具有标度不变性的对象必定满足自相似性[21]。而对于轨道不平顺这种自然界中的分形现象而言，其自相似性应表现为统计自相似；统计自相似可以由统计自相似度来定量描述，统计自相似度是由对尺度和测度线性回归的相关系数以及相关系数的临界值来定义的[22]，即

(1)

(2)

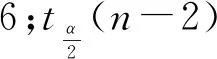
为了说明轨道不平顺的统计自相似度，本文这里采用华东地区某高铁线路2020年5月轨检车测得的动态不平顺数据作为样本来源，轨道类型为CRTS Ⅱ型板式无砟轨道，设计速度为350 km/h，日均发车频率为140对，线路运营速度为300 km/h；轨道综合检查车为CRH380AJ-0203，检测速度284 km/h，检测波长范围为1.5～120.0 m，采样间隔为0.25 m。

根据TB/T 3352—2014《高速铁路无砟轨道不平顺谱》的相关规定，轨道不平顺样本选取长度为1 024 m、基础形式为简支梁桥的左高低不平顺数据作为分析对象。数据样本及其功率谱如图2所示。

通过对图2(b)的线性区域进行最小二乘线性回归，采用功率谱密度法的计算公式可得到分形维数D为0.566 4，线性回归的相关系数r为0.956 6，如表1所示。利用式(1)和式(2)可得相关系数r的临界值，rα(n-2)为0.759 3，统计自相似度ρα为0.966 1。而统计自相似度越接近1则说明自相似程度越高，因此，可以表明轨道不平顺具有显著的统计自相似性特征。结合其标度不变性结论，可以确定轨道不平顺时域波形具有显著的分形特征。

图2 数据样本及其功率谱

表1 各种分形维数计算方法及公式

1.2 分形维数计算方法

对于具有显著分形特征的曲线进行定量化描述，一般是采用分形维数的方法；目前尚无统一的标准对所需采用的计算方法进行界定，通常是根据所研究对象的特征，利用盒维数法、尺码法、功率谱密度法、结构函数法和变差法等进行计算[23]。这些方法中目前应用最为广泛的是盒维数法，已应用于轨面不平顺评价[24]和无砟轨道伤损的识别中[25]；而针对于轨道不平顺，既有Hyslip和Landgraf等的研究采用的是尺码法，但计算步长实际上表征了不同的波长特征，不同线路呈现出的波长特征有显著差异性，且列车的动力影响也较大，因此，导致计算的轨道不平顺分形维数具有典型的不稳定性；而关于高速铁路无砟轨道不平顺的分形维数研究，目前就作者所知尚无相关的报告。所以，需要深入地讨论高速铁路无砟轨道不平顺分形维数的表征方法。

一般而言，分形维数是通过对双对数坐标系中尺度和测度的线性区域进行最小二乘线性回归、利用回归直线的斜率与分形维数存在一定的数学关系来获取的，表1为各种分形维数测定方法及其计算公式。

2 无砟轨道不平顺分形维数计算方法比选

2.1 分形维数计算方法有效性验证

作者采用MATLAB软件对1.2节相关算法进行实现，为了验证算法的有效性，进而分析各种算法的适用性，需要对算法进行比较。鉴于Weierstrass-Mandelbrot函数在形状和波动程度上与轨道不平顺相似度较高且广泛用于不平度的模拟(如路面不平度等)和分形算法的评价，因此，本文选取Weierstrass-Mandelbrot函数进行分析。

Weierstrass-Mandelbrot函数是具有自相似性、标度不变性和确定分形维数的理想分形曲线[26]，其具体表达式如下

(3)

式中：Z(x)为随机轮廓高度；x为轮廓的位置坐标;G为特征尺度系数;D为分形维数，λn为轮廓的空间频率。

根据验算结果，G取为0.01，λ取为1.5，x在[1,2]间取值，一般可以通过改变D值来获取分形维数介于1～2的W-M曲线。D为1.2、1.4、1.6、1.8时的W-M曲线如图3所示。

图3 不同D值的W-M曲线

对上述W-M曲线进行计算，各种方法的计算值与理论值间的误差如图4所示。

图4 误差分析

由图4可知，盒维数法、尺码法、功率谱密度法、结构函数法和变差法计算所得分形维数值的平均相对误差值分别为8.42%、10.97%、13.17%、1.91%和6.13%，即结构函数法计算得到的平均相对误差最小，功率谱密度法则平均相对误差最大。而平均相对误差越大，说明计算中尺度与测度的线性关系越差，线性回归的相关系数也就越低。所以，对于与轨道不平顺特征相类似的W-M曲线而言，结构函数法和变差法的计算结果相对精度较高。后文中，将采用这两种方法进行轨道不平顺的分形维数计算，进一步讨论适用于轨道不平顺分形维数的最佳计算方法。

2.2 轨道不平顺分形维数计算方法的适用性分析

由于Hyslip和Landgraf等的研究中已采用了尺码法进行了计算，因此，本文选取了尺码法、结构函数法和变差法3种方法进行轨道不平顺分形维数的分析。

图5所用数据与1.1节中所述数据来源一致。为了说明轨道不平顺的统计自相似度，采用华东地区某高铁线路2020年5月轨检车测得的动态不平顺数据作为样本来源，轨道类型为CRTS Ⅱ型板式无砟轨道，设计速度为350 km/h，日均发车频率为140对，线路运营速度为300 km/h；轨道综合检查车为CRH380AJ-0203，检测速度284 km/h，检测波长范围为1.5～120.0 m，采样间隔为0.25 m。由于高低和轨向不平顺是高速列车垂向和横向振动的主要激励源[27]，因此，本文这里将此两种类型的轨道不平顺作为对象进行研究。

图5 轨道不平顺时域样本

由图6和表2可知，3种方法计算得到的分形维数具有显著的差异性，根本性原因在于算法的差异性而导致计算斜率表现形式不同，而计算斜率的分段表达，使得分形维数出现了不同的区段值。变差法的算法鲁棒性较好，无标度区间宽，计算结果为单一的维数，且线性回归的相关系数较为理想，对轨道不平顺曲线的适应性较好。另外两种方法，特别是尺码法，曲线分段趋势明显，且不同类型的轨道不平顺曲线分段也有所不同；结构函数法则同样呈现不同分形维数的分段结果。值得注意的是，上述不同算法中，曲线分段点具有显著的不稳定性，不同的样本计算结果分段点有所不同，这与文献[28]结论一致；因此，为了方便应用和计算，对于高速铁路无砟轨道不平顺应该采用变差法进行分形维数的计算。将采用变差法对全年累计的轨道不平顺检测数据进行分析，以进一步说明分形维数在轨道区段质量管理应用的有效性。

图6 分形双对数图

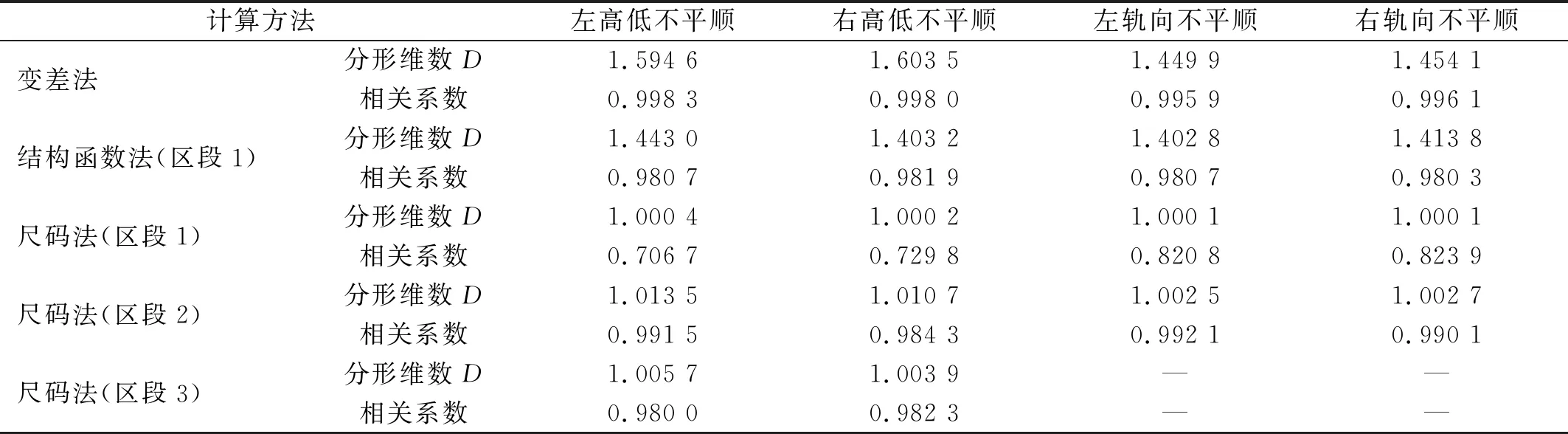
表2 实测轨道不平顺分形维数计算结果

3 轨道区段质量的评估

3.1 分形维数与TQI相关性分析

为了说明利用分形维数对轨道区段质量进行评估的可行性和合理性，需要将分形维数与现有评价指标进行比较。轨道质量指数是定义区段轨道质量状态的综合性指标，是铁路管理部门对轨道质量状态进行管理和制定养护维修计划的重要依据。因此，本文首先讨论了TQI与分形维数之间的相关性。

大量的样本是统计分析的前提，这里选用100 km的轨道不平顺动态检测数据、数据来源同前，样本点数为400 000，参照TQI管理中要求的200 m长度进行分段，分别计算高低和轨向不平顺的单项TQI和分形维数间的相关系数，结果如图7所示，可知轨道不平顺分形维数总体变化趋势与TQI变化趋势一致，即分形维数在某种程度上可以有效地反映区段轨道质量的变化趋势。

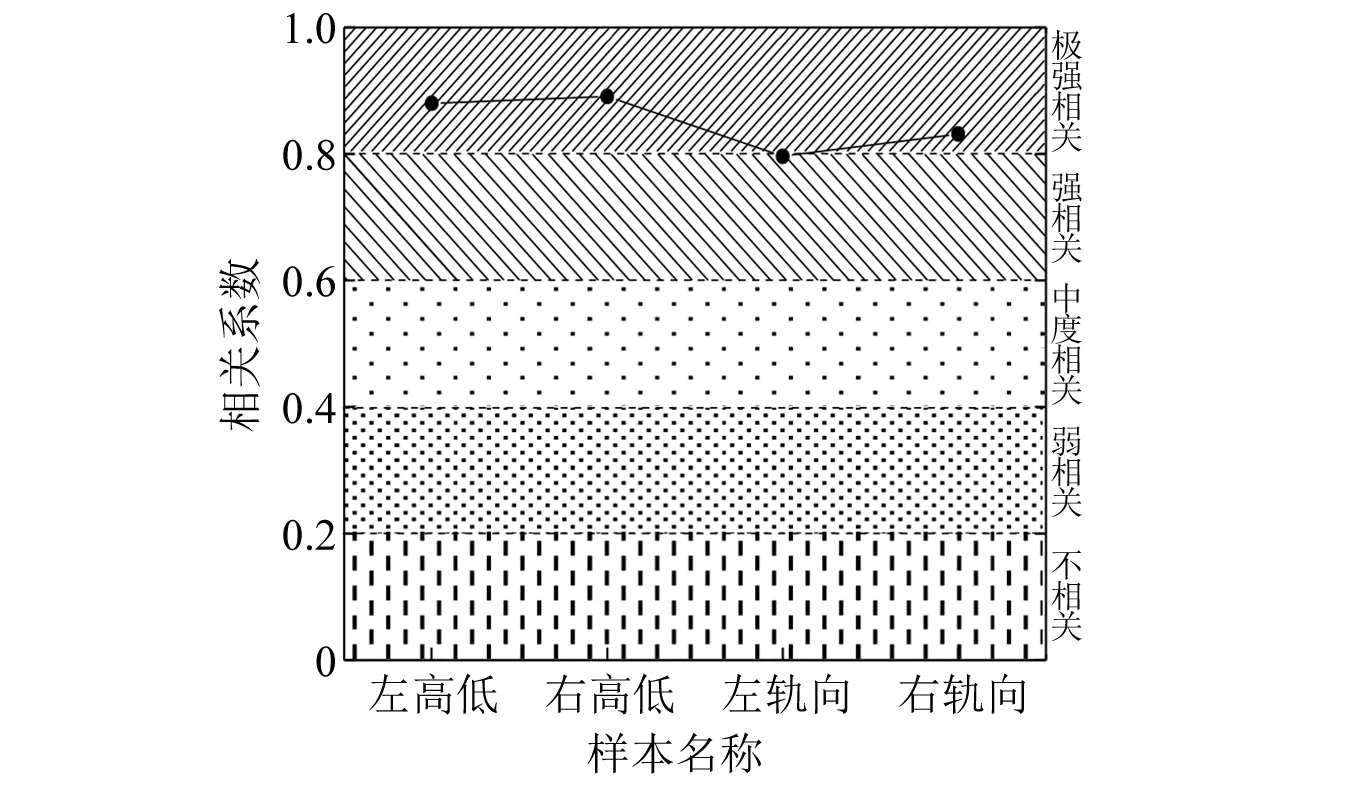
图7 相关性分析

3.2 实例分析

这里分析的线路同前，只是数据样本的检测时间范围为2019年1月—2019年12月，共计23次检测数据。同样计算200 m区段的高低不平顺、轨向不平顺的单项TQI和分形维数，以及区段整体的TQI和分形维数之和，其计算结果如图8所示，分别对计算结果线性拟合，研究分形维数和TQI的变化规律。

图8 典型单元区段累计全年的计算结果

由图8可知，轨向不平顺单项TQI与分形维数变化规律较为近似，均逐渐变大，说明了轨向不平顺的逐渐恶化趋势。高低不平顺单项TQI和区段整体的TQI变化规律则与轨向不平顺有较大的差异性，即在1月—7月呈现逐渐增大的趋势，而在夏季突然变大，这主要是由于无砟轨道内部温度应力较大而使得轨道板变形映射到高低不平顺所引起的。而夏季分形维数则表现较为稳定，这是因为分形维数主要反映轨道不平顺曲线充满空间的能力以及曲线的疏密程度和波动程度，对于样本幅值变化不敏感，所以其变化较小甚至较为稳定。经过夏季针对性地保养和维修，9月份之后高低不平顺单项TQI和区段整体的TQI有明显的下降，区段质量状态有了显著的改善，即图中产生了“台阶”。而在维修保养之后高低不平顺单项TQI和区段整体TQI均呈现较为稳定的结果，变化较小。但是对于高低不平顺的分形维数以及区段的分形维数之和则呈现了一直增大的趋势。因此，对比TQI幅值可知，线路短暂性的维修保养对于轨道不平顺分形维数影响较小，即使经过了针对性维修保养，虽然表面上降低了TQI值，控制了高低不平顺的进一步恶化，但本质上轨道区段仍然还是处于逐渐恶化的状态，分形维数具有表征轨道结构实质状态的能力，这是目前TQI管理所不具备的。同样值得注意的是，TQI与分形维数的波动范围较小，说明目前线路的几何状态是较为稳定的，可以保证高速列车的运营安全。

所以，综上可知，不同类型的轨道不平顺的分形维数与单项TQI指数关系不同，但对于区段质量而言，分形维数呈现了逐渐变大的趋势，可以表示为轨道区段服役状态的逐渐劣化现象，这无疑为线路轨道的预防性维修提供了有效的指导，可通过深化分析其变化规律来合理地安排维修周期和维修量。

4 结 论

本文讨论了高速铁路无砟轨道不平顺的分形特征，确定了轨道不平顺分形维数的计算方法，并给出了无砟轨道线路状态劣化的典型结果，可以得到以下结论：

(1)轨道不平顺具有典型自相似性和标度不变性的分形特征。

(2)不同分形维数计算方法对于轨道不平顺进行计算，其结果具有显著差异性，变差法呈现计算精度较高、无标度区间宽、鲁棒性强等特点，建议采用变差法进行轨道不平顺的分形维数计算。

(3)分形维数可以有效地表征轨道服役状态逐渐恶化的趋势，受线路作业维修干扰较少，这个无疑为轨道预防性维修提供了的有益补充，未来可进一步的深入研究，分析分形维数与轨道劣化速率的关系，形成有效地轨道区段质量管理方法。