基于数学建模思想的“解三角形的应用”教学设计

刁志瑞 叶慧妍 卢 韫

[摘  要] 基于以往“解三角形应用”课堂中容易出现例子断裂分割，缺乏联系而造成的学习障碍，文章将重新从数学建模的视角，通过设计完整的探险故事，在问题解决的过程中整体联系解三角形应用模型，从而培养学生的建模意识和建模能力.

[关键词] 数学建模;解三角形的应用;解三角形;教学设计

《普通高中数学课程标准（2017版）》提出重视培养学生的六大数学核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析. 数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养，也是数学学习过程中学生需要掌握的重要思想和能力. 数学建模构建了数学与现实世界的桥梁，是数学应用于生活，生活联系数学的重要形式. 因此，在数学教学中有意识地基于数学建模思想设计课程，将有助于让学生感悟数学与现实世界的关联，进一步感受数学的应用价值，体会数学的应用之美;同时利用数学建模过程充分发展学生分析问题和解决问题的能力，培养其良好的数学素养.

“解三角形的应用”与现实生活有着密切联系. 如何能够将数学建模思想贯穿于课程中，又不显得与生活脱节而无趣呢？为此，本文将基于数学建模思想，在“解三角形的应用”一课中，通过创设有趣、完整的探险故事，统领解三角形应用的几种数学模型，让学生能够在“问题解决中学习”，实现在课程中培养建模思想和建模能力的目标.

教材分析

天文观测、航海和地理测量是人类认识自然的重要方面，而解三角形的理论在其中发挥了重要作用. 同时，数学发展历史上，受到天文测量、航海测量和地理测量等方面实践活动的推动，解三角形的理论也得到不断发展，并被用于解决许多测量问题. 在初中，我们已经能够借助于锐角三角函数解决有关直角三角形的一些测量问题. 然而在实际工作中我们还会遇到许多其他的测量问题，这些问题仅用锐角三角函数就不够了，如：怎样在航行途中测出海上两个岛屿之间的距离？怎样测量底部不可到达的建筑物的高度？这些问题的解决需要应用本章学习的正弦定理与余弦定理.

本节内容选自人教A版高中数学必修五第一单元1.2节“解三角形应用举例”. 《普通高中数学课程标准（2017版）》指出“能用余弦定理、正弦定理解决简单的实际问题”，因此本节解三角形的应用是在前面正弦、余弦定理学习的基础上进一步把其迁移到实际问题的重要知识，是实际问题与数学知识相结合的典型案例，能够充分体现数学建模在实际问题中的优势和力量，是培养学生数学抽象、数学建模的重要教学内容.

学情分析

1. 认知基础

本节课针对成绩中等偏上的学生设计，在这之前学生已经学习过三角函数的诱导公式、正弦定理和余弦定理，对这些内容有比较透彻的理解，并且经过高中数学的学习，已经积累了一定的数学活动经验，具备一定的数学抽象能力.

2.认知障碍

虽然已经掌握正弦定理与余弦定理，但学生对于实际问题中解三角形的应用还不熟悉，对于现实问题的抽象与三角形模型的构建存在一定困难，数学建模能力有待进一步加强.

教学目标

1.知识与技能：了解解三角形在实际生活中的广泛应用;能够利用解三角形相关知识构建数学模型解决常见的实际问题.

2.过程与方法：通过讲故事的学习形式，在解决实际问题的过程中感受解三角形应用的价值，感知数形结合、分类讨论和数学建模的思想方法，丰富数学建模与活动经验.

教学重难点

1.教学重点：解三角形的应用.

2.教学难点：实际问题中解三角形的建模方法.

教学过程

1. 复习引入

师：在之前的课程中，我们学习了正弦定理、余弦定理及其证明，也鼓励大家课下积极探索多样的证明方式. 下面，我们首先复习一下这两个定理.

正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即==.

余弦定理：三角形中任何一边的平方等于其他两边的平方和减去这两边与它们的夹角的余弦的积的两倍，即a2=b2+c2-2bccosA，b2=a2+c2-2accosB，c2=a2+b2-2abcosC.

师：事实上，正弦定理和余弦定理在实际测量中有许多应用，尤其是古代. 下面，让我们回到古代，使用古人的工具（测角仪和皮卷尺）来感受这两个定理的魅力.

2. 情境探究

时间回到古代，这时候按照藏宝图，你带着测角仪、皮卷尺和指南针来到了一座小岛上. 接下来，你将根据藏宝图的指示，灵活使用手中的测量工具去寻找宝藏. 藏宝图显示，寻宝的起点是一棵有特殊标记的高大树木. 经过比对，你走到了这棵树的旁边，打开了藏宝图……

指示1：（例题）请沿西南方向走一段距离，该距离为两倍树木高度，走过这段距离，你将看到一个瞭望台.

师：凭借手中的指南针，我们可以确定下一步走的方向，但如何用测角仪、皮卷尺测量树高呢？（给出示范，如图2）

师：测角仪可以测出视角，皮卷尺可以测出你与树木之间的距离，这样就构成了已知一个锐角和一条直角边的直角三角形，根据l1=d1·tanα求出树木高度. 我们称这种高度测量为“底部可到达”.

设计意图：本题属于解三角形中的基础题型，主要目的是通过演示和简单讲解，让学生熟悉情境，并利用情境中已有的工具测量树高，了解实际情境中解三角形的应用概况，构造三角形，寻找已知量. 本题只需要根据树木与地面垂直的隐含条件构造一个直角三角形即可求解，是高度测量中底部可到达的最容易的类型，用于熟悉情境和引入相对恰当.

指示2：请测量瞭望台顶部高度，并向东走一段距离，该距离为五倍瞭望台顶部高度. 在那里，你将隔着海面看到一座灯塔.

师：与上一個指示类似，这时你依然可以走到瞭望台旁，但你需要测它的一部分高度，这种情况下，仅构造一个三角形够吗？请同学们动手试一试. 完成的同学可以上台演示你的做法.

此时，需要构造两个直角三角形，l2=d2（tanγ-tanβ）.

设计意图：本题属于解三角形中的基础题型，代表了高度测量中的“底部可到达”，但未知量是建筑中的一部分，是第一个例题的变式，此时需要选择. 此题依然不涉及复杂的推理过程，相对容易，主要目的是让绝大多数学生体会从实际情境中构建数学模型的数学抽象过程，并初步使用情境中给出的工具，体会测量中的数学，感受数学知识的应用价值.

指示3：请你测量灯塔的高度，并沿着海岸向南走一段距离，该距离为三倍塔高. 在那里，你将隔海看到一艘游轮.

师：此时，我们已经不能测出灯塔与自己的距离. 要如何转化呢？需要构造几个三角形呢？请同学们4人一组，进行讨论. 有想法的小组可以演示.

此时需要构造两个直角三角形，根据三角形中的两个等量关系可以求出两个未知量，其中一个即为塔高l3. （m1+d3）tanα2=m1tanα1？圯m1=？圯l3=.

设计意图：本题为测高度的第三种类型——底部不可达，相对前面两题难度有提升. 仍需要构造两个直角三角形，但此时观察者不再是站在原地改变视角，而是通过改变自己的位置，创造出多个已知量，进一步解决问题. 这一情境是上一题的变式练习，通过这一问题，学生对从实际问题出发构造三角形应有更深刻的认识.

指示4：你现在可以看到一艘大船了吗？恭喜，你已经离宝藏很近了——它就在船上. 但你还需要测量出船到岸边的距离，来搭建一个上船需要的桥，你会怎么做呢？

师：在这个情境中，我们需要测量一段未知的距离. 现在仅有两个点，我们需要构造三角形吗？如果要的话，需要构造几个三角形？请同学们4人一组，进行讨论. 有想法的小组可以演示.

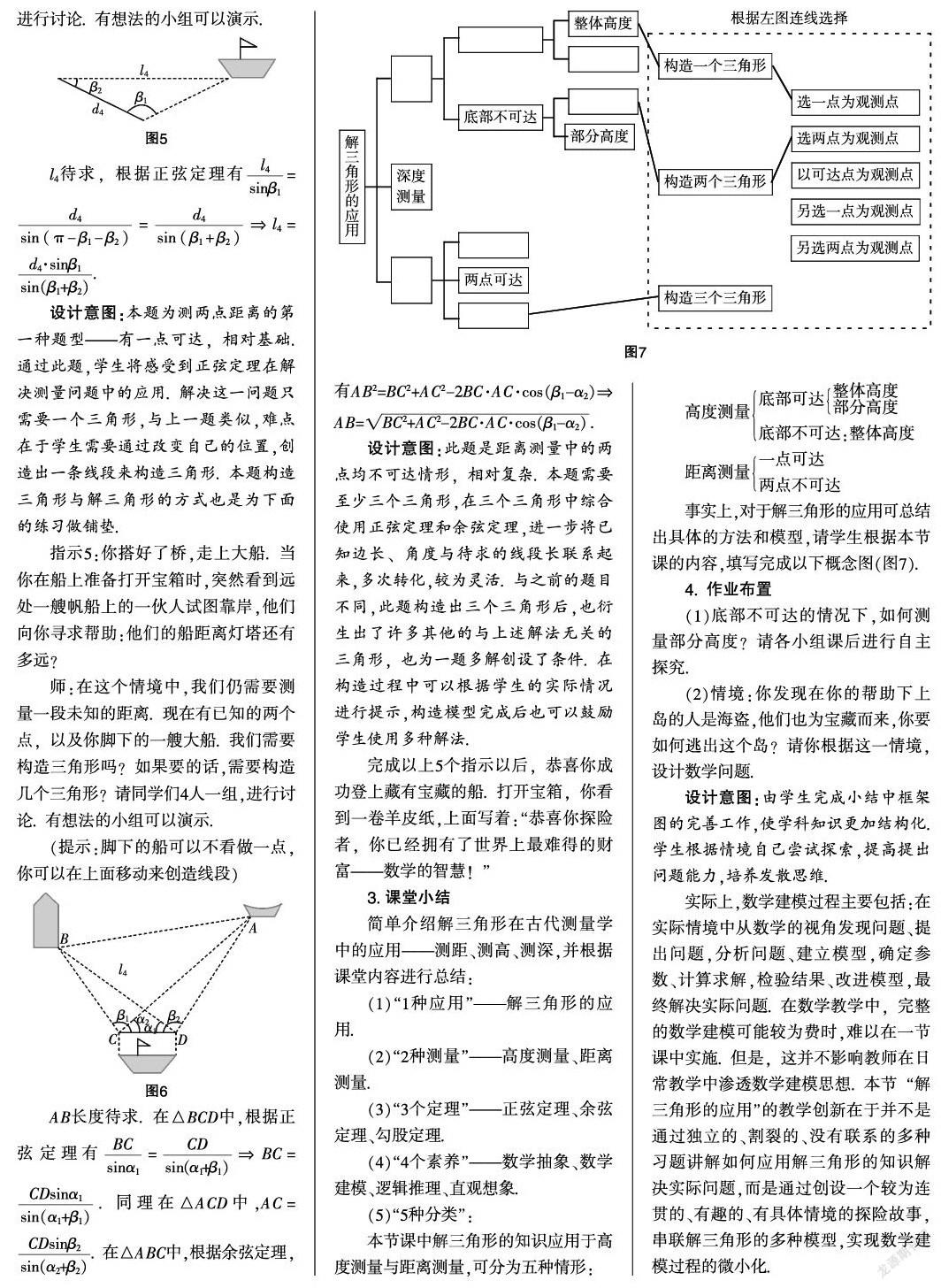
l4待求，根据正弦定理有==？圯l4=.

设计意图：本题为测两点距离的第一种题型——有一点可达，相对基础. 通过此题，学生将感受到正弦定理在解决测量问题中的应用. 解决这一问题只需要一个三角形，与上一题类似，难点在于学生需要通过改变自己的位置，创造出一条线段来构造三角形. 本题构造三角形与解三角形的方式也是为下面的练习做铺垫.

指示5：你搭好了桥，走上大船. 当你在船上准备打开宝箱时，突然看到远处一艘帆船上的一伙人试图靠岸，他们向你寻求帮助：他们的船距离灯塔还有多远？

师：在这个情境中，我们仍需要测量一段未知的距离. 现在有已知的两个点，以及你脚下的一艘大船. 我们需要构造三角形吗？如果要的话，需要构造几个三角形？请同学们4人一组，进行讨论. 有想法的小组可以演示.

（提示：脚下的船可以不看做一点，你可以在上面移动来创造线段）

AB长度待求. 在△BCD中，根据正弦定理有=？圯BC=. 同理在△ACD中，AC=. 在△ABC中，根据余弦定理，有AB2=BC2+AC2-2BC·AC·cos（β1-α2）？圯AB=.

设计意图：此题是距离测量中的两点均不可达情形，相对复杂. 本题需要至少三个三角形，在三个三角形中综合使用正弦定理和余弦定理，进一步将已知边长、角度与待求的线段长联系起来，多次转化，较为灵活. 与之前的题目不同，此题构造出三个三角形后，也衍生出了许多其他的与上述解法无关的三角形，也为一题多解创设了条件. 在构造过程中可以根据学生的实际情况进行提示，构造模型完成后也可以鼓励学生使用多种解法.

完成以上5个指示以后，恭喜你成功登上藏有宝藏的船. 打开宝箱，你看到一卷羊皮纸，上面写着：“恭喜你探险者，你已经拥有了世界上最难得的财富——数学的智慧！”

3.课堂小结

简单介绍解三角形在古代测量学中的应用——测距、测高、测深，并根据课堂内容进行总结：

（1）“1种应用”——解三角形的应用.

（2）“2种测量”——高度测量、距离测量.

（3）“3个定理”——正弦定理、余弦定理、勾股定理.

（4）“4个素养”——数学抽象、数学建模、逻辑推理、直观想象.

（5）“5种分类”：

本节课中解三角形的知识应用于高度测量与距离测量，可分为五种情形：

高度测量底部可达整体高度部分高度底部不可达：整体高度

距离测量一点可达两点不可达

事实上，对于解三角形的应用可总结出具体的方法和模型，请学生根据本节课的内容，填写完成以下概念图（图7）.

4. 作业布置

（1）底部不可达的情况下，如何测量部分高度？请各小组课后进行自主探究.

（2）情境：你发现在你的帮助下上岛的人是海盗，他们也为宝藏而来，你要如何逃出这个岛？请你根据这一情境，设计数学问题.

设计意图：由学生完成小结中框架图的完善工作，使学科知识更加结构化. 学生根据情境自己尝试探索，提高提出问题能力，培养发散思维.

实际上，数学建模过程主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题. 在数学教学中，完整的数学建模可能较为费时，难以在一节课中实施. 但是，这并不影响教师在日常教学中渗透数学建模思想. 本节“解三角形的应用”的教学创新在于并不是通过独立的、割裂的、没有联系的多种习题讲解如何应用解三角形的知識解决实际问题，而是通过创设一个较为连贯的、有趣的、有具体情境的探险故事，串联解三角形的多种模型，实现数学建模过程的微小化.