钢波纹管涵洞板厚优化有限元分析

何 强，刘百来，滕文刚

（1.西安工业大学，陕西 西安 710021；2.西安中交土木科技有限公司，陕西 西安 710075）

引言

金属钢波纹管的波纹结构可使涵洞路面受力合理[1]，解决不同恶劣环境下桥涵混凝土结构的破坏等复杂问题[2]，而且钢波纹管涵综合造价低于同类混凝土涵洞，既提高了适应基础变形的能力[3]，又有利于绿色协调、经济环保。从结构功能与本构关系角度分析，钢波纹管结构的强度来自于上覆土与结构的土拱作用[4]。且轴向波纹具有特殊的受力特性，轴向和径向能共同承担载荷，使抗变形能力增强[5]。

运用有限元软件对钢波纹管涵洞的应力变形进行计算分析，通过建立模型分离单元，对单孔直径6 m 的钢波纹管涵洞在覆土作用下应力和变形进行计算[6]，分析不同波峰波谷断面，不同角度等效应力，通过更换不同钢波纹板片的板厚，对钢波纹管结构的应力变形的影响，得出规律和结论。

1 钢波纹管模型建立与计算

1.1 计算模型

几何模型是由钢波纹管结构主体和周围土体两部分共同组成，钢波纹管为Q355 钢，选用直径6 m、波形380 mm×140 mm、壁厚10 mm 的钢波纹圆管。管顶覆土分层回填，每层覆土高度为1 m，管顶覆土高度为10 m。

1.1.1 定义单元类型

钢波纹管主体采用适用于结构的薄壳单元shell63，管顶填土选用接近土体材料性质的三维实体单元solid45。

1.1.2 选择材料属性

计算中涉及到钢波纹管、填土两种不同材料类型，各种材料力学参数根据实际工程案例，并参考《公路桥涵设计通用规范》（JTG D60—2015）进行选取，表1 为计算时所用材料参数。

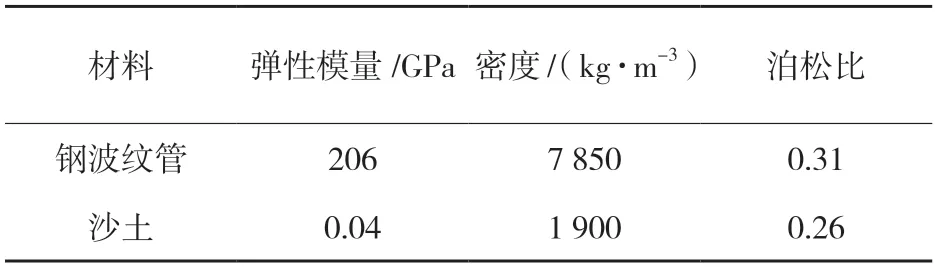
表1 模型材料参数

1.1.3 网格划分

进行土体和钢波纹管网格的划分是模型建立的重点，采用扫掠网格划分方式对钢波纹管主体和周围土层进行网格划分。

1.1.4 初始条件与边界条件

运用有限元计算时，以自重应力场为主。模型左、右边界分别取水平X 轴正、负方向，下边界取地基基础作为底面，计算整个模型时，左右边界施加水平位移约束，下边界施加全约束。

1.1.5 有限元钢波纹管优化模拟方案

对覆土钢波纹管优化前后,管顶覆土均为10 m，而优化前钢波纹管壁厚10 mm，优化后将水平位置（0°和180°）增加板厚3 mm 作为加强，再分别对应力变形进行计算分析。

按照管周不同角度模拟分析，分别提取波峰波谷断面沿管周角度（0°、45°、90°、135°、180°、225°、270°和360°）的等效应力，同时提取0°、90°、180°和270°的水平、竖向位移，见图1，建立土体和钢波纹管结构的有限元计算模型见图2、图3。

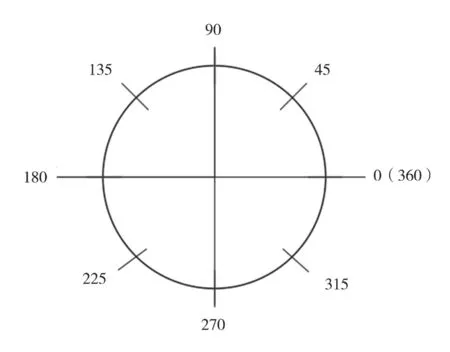
图1 钢波纹管管周角度（°）

图2 钢波纹管划分网格模型

图3 土-钢结构划分网格模型

1.2 计算结果分析

通过有限元计算分析管顶覆土高度10 m 的钢波纹管涵洞，将水平0°和180°板厚增加3 mm，作为加强，可得钢波纹管板厚优化前后等效应力和位移云图。

1.2.1 覆土作用下钢波纹管优化前后等效应力

由图4、图5 可以看出：上部管顶覆土下，钢波纹管最大等效应力在水平X 轴方向均未发生变化，而覆土作用下最大等效应力的数值大小发生了变化，由152 MPa 减小到130 MPa，应力变化较为明显。

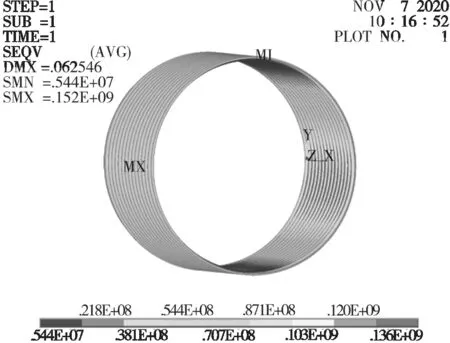
图4 钢波纹管优化前等效应力云图

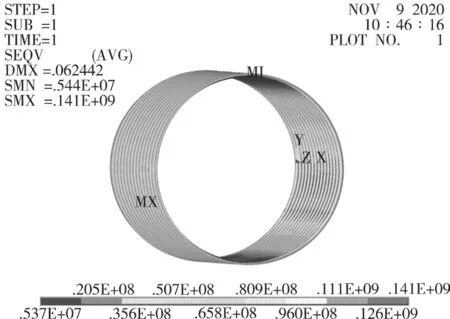
图5 钢波纹管优化后等效应力云图

1.2.2 覆土作用下钢波纹管优化前后位移

优化前后水平位移云图见图6、图7。可以看出：优化前后水平位移均没有发生变化，两张水平位移结果云图相同。

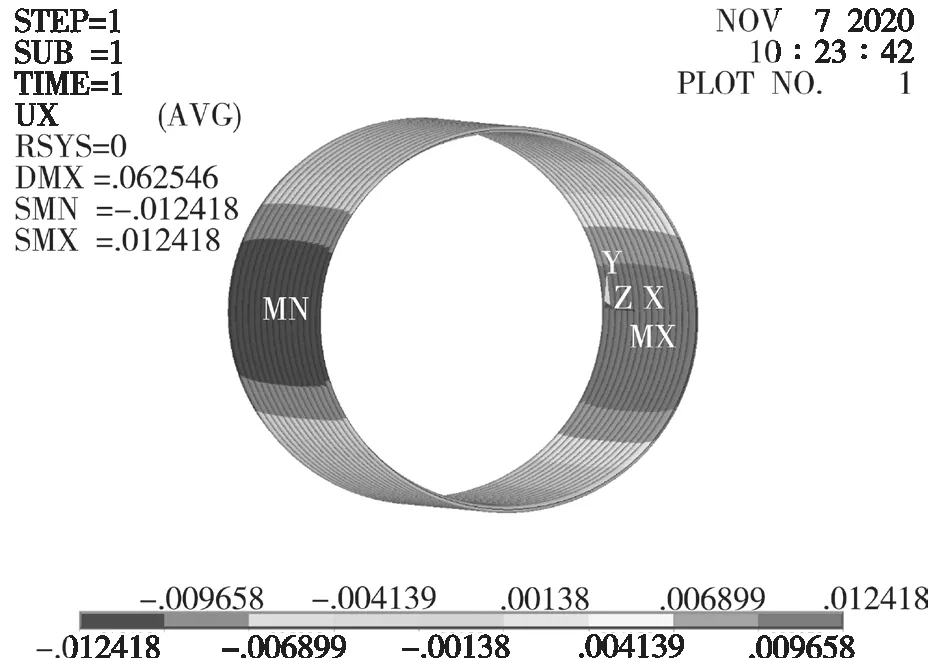
图6 钢波纹管优化前的水平位移云图

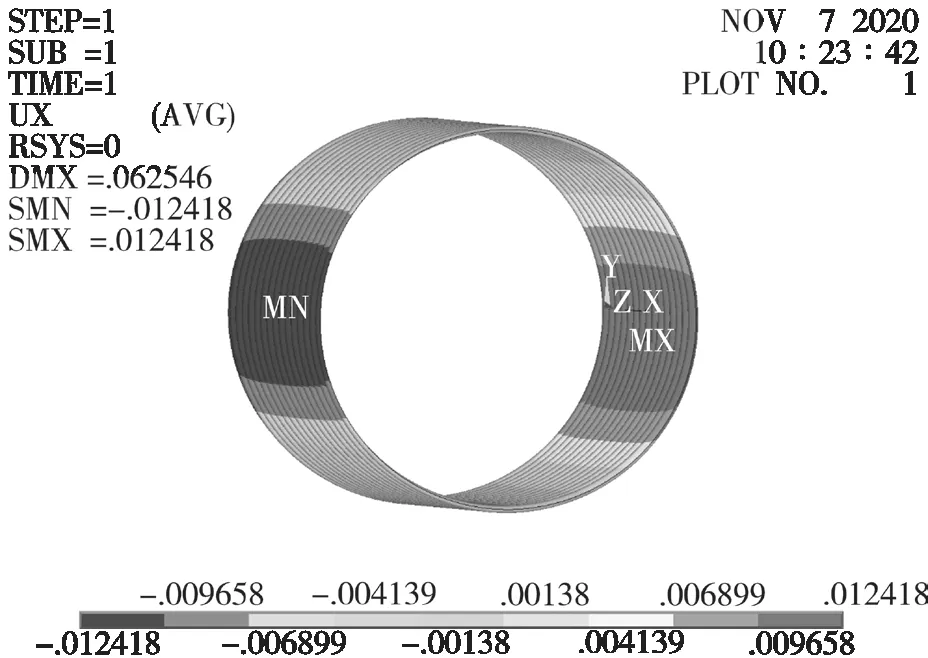
图7 钢波纹管优化后的水平位移云图

优化前后竖直位移云图见图8、图9。可以看出：最大竖向位移在管顶，相对竖向位移最大值均出现在管顶和管底，优化前后变形量仅减小了0.9 mm，对竖向位移影响较小。

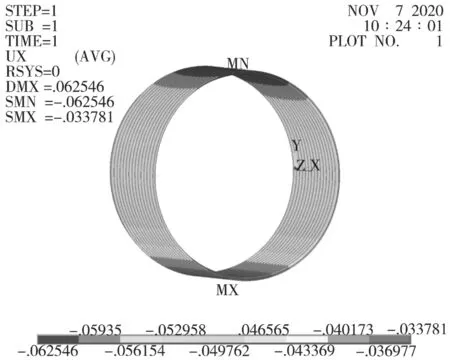
图8 钢波纹管优化前的竖向位移云图

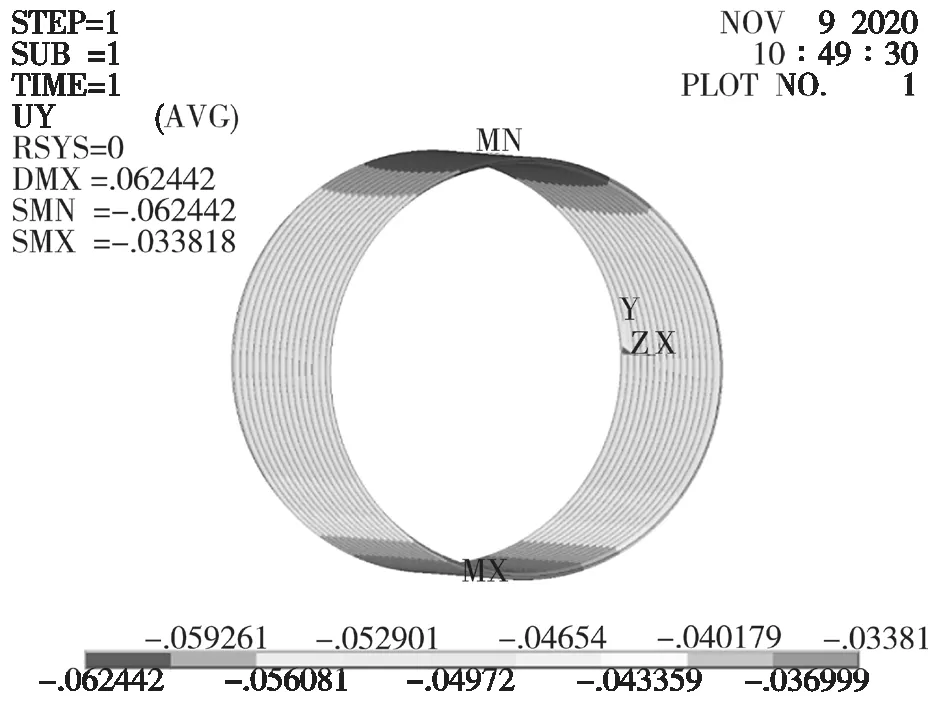
图9 钢波纹管优化后的竖向位移云图

2 钢波纹管计算结果优化分析

2.1 钢波纹管性能优化概述

在实际工程中提高钢波纹板结构性能的方式通常有两种：一是提高钢材的屈服强度；二是通过优化结构形式，减小其产生的应力变形。采用优化钢波纹板板片结构形式进行研究分析，通过调整钢波纹管的板厚来减缓钢波纹管的等效应力，分散上部传递的均布荷载，从而减小钢波纹管内部应力和变形。分析相同工况和截面波段下，优化前后波峰、波谷处的应力以及钢波纹管的水平、竖向位移。

2.2 优化前后波峰和波谷不同角度应力对比

依据有限元计算结果，分别提取钢波纹管波峰、波谷断面沿管周角度（0°、45°、90°、135°、180°、225°、270°和360°）的等效应力，得出优化前后管周应力变化规律。

2.2.1 优化前后波峰应力的变化规律

优化前后波峰应力的变化规律见图10。分析得出：（1）波峰位置处，优化前，应力值随着角度的变化具有周期性规律，分别在0°、180、和360°位置处出现较大应力，最大应力出现在180°附近为149.64 MPa；在90°和270°位置应力值表现相对较小，90°位置出现最小应力值为16.58 MPa，其余各角度的应力值趋于稳定。（2）优化后，应力值随角度变化规律与优化前相似，相比总体等效应力值在减小，在0°、180、和360°位置出现较大应力，最大仍在180°附近为127.94 MPa；在90°和270°位置应力值比优化前略有偏大，90°应力值为21.74 MPa，其它各角度应力值总体小于优化前。（3）优化前后，波峰位置处的最大应力由149.64 MPa 减小到127.94 MPa，减小了21.7%，而最小应力由16.58 MPa增加到21.74 MPa，增加了5.16%，其它各位置等效应力均小于优化前。说明在钢波纹管水平0°和180°位置增加钢波纹板片的厚度，总体上能使等效应力明显减小，减缓了钢波纹管在覆土作用下的应力值。

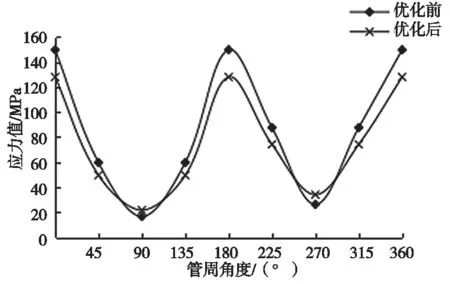
图10 波峰等效应力变化规律

2.2.2 优化前后波谷应力的变化规律

优化前后波谷应力的变化规律见图11。分析得出：（1）优化前，与波峰不同的是，在0°和180°位置处，波谷应力值较小，最小值在0°位置处为54.26 MPa；然而在270°位置，最大等效应力值为112.39 MPa，在315°时，波谷处的应力值大小与波峰处应力值接近，整体来看，波谷随角度变化趋势与波峰不同，同一角度等效应力值相差较大。（2）优化后，波谷应力变化规律与优化前相似，但总体等效应力值小于优化前，最大等效应力的位置仍出现在270°，数值大小为100.46 MPa；应力在0°和180°位置较小，最小应力值为41.15 MPa。各角度处应力值随角度变化规律：先增大→减小→增大→减小。（3）优化前后的波谷等效应力值均小于优化前，等效应力值出现的角度不变，最大等效应力由112.39 MPa 减小到100.46 MPa，同比减小了11.93%，而最小应力从54.26 MPa 减小到41.15 MPa，同比减小了13.11%，说明在钢波纹管0°和180°位置增加钢波纹板片的厚度，可以减小钢波纹管在覆土作用下的应力，提高钢波纹管整体强度和刚度。

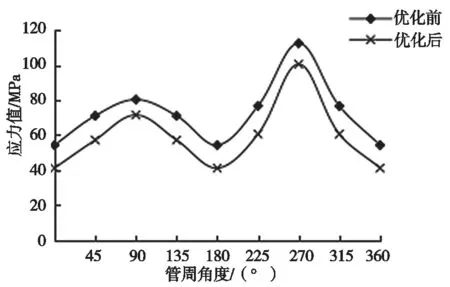
图11 波谷等效应力变化规律

2.3 优化前后最大等效应力对比

依据有限元计算结果，提取钢波纹管优化前后的最大等效应力与角度，见表2。

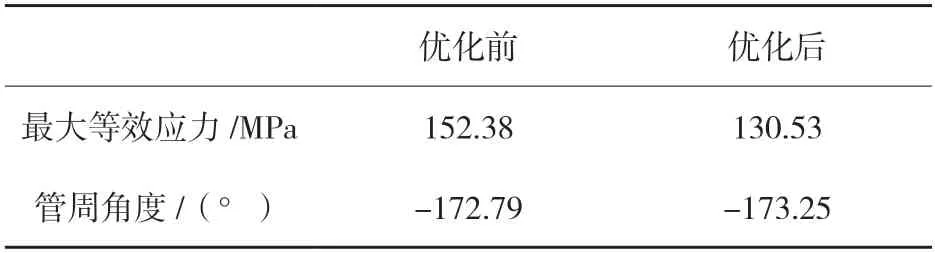
表2 最大等效应力对比

由表2 可以看出：优化前后最大等效应力发生了较为明显的变化，优化后的最大等效应力明显减小，而最大等效应力出现的角度变化在180°附近。因此，在水平0°和180°位置增加钢波纹管板片的厚度可以显著地减小最大等效应力，缓解上部因土体荷载作用而引起的应力集中。

2.4 优化前后钢波纹管位移对比

根据有限元计算结果，提取钢波纹管优化前后0°、90°、180°和270°的水平、竖向位移，见表3。

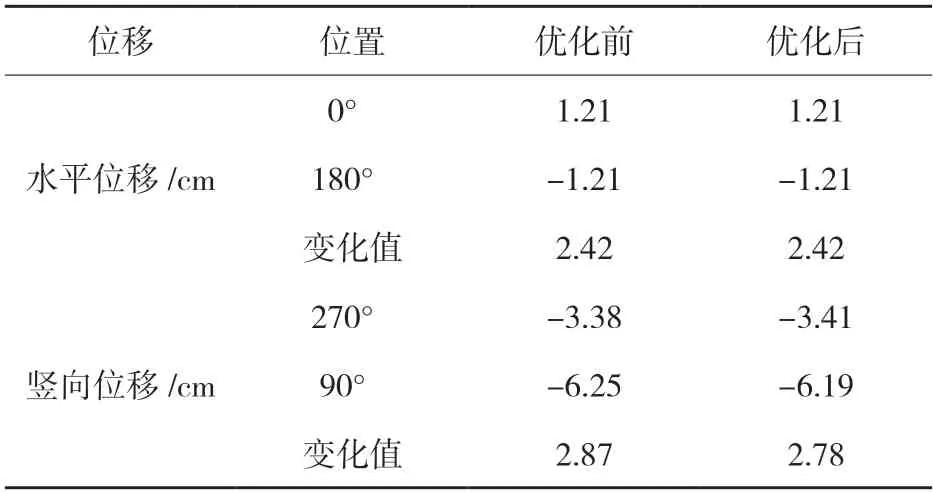
表3 优化前后钢波纹管位移对比

由表3 可得：优化前后，水平相对位移没有变化，而竖向位移优化前后变化较小，由2.87 cm 减小至2.78 cm。总体来看，通过调整钢波纹管在0°和180°位置的板片厚度，对水平位移没有影响，对竖向位移影响较小，仅为0.9 mm。对比可得：管顶覆土10 m 下，相同角度优化前后最大等效应力发生了明显变化，总体应力值变小；而从水平、竖向位移来看，总体趋于稳定，并无较大变化。因此，通过在0°和180°位置增加钢波纹管板厚的方法，可以减小钢波纹管不同角度的等效应力，使整体更加安全稳定。

3 结语

（1）同一波段的内侧波峰位置处，优化前后，钢波纹管的最大应力均出现在管周0°、180°位置；波谷位置应力分布与波峰不同，最大等效应力在管底270°，其余角度等效应力无较大的变化。（2）最大等效应力出现在管周180°附近，优化前后最大等效应力差异明显，数值减小约18 MPa。优化后，水平位移未发生变化，竖向位移比优化前增加0.9 mm，优化前后对钢波纹管的变形影响较小。（3）通过对比分析优化前后钢波纹管的最大等效应力和水平、竖向位移变化情况，得出调整0°、180°的钢波纹管板厚可以减小不同角度的等效应力，提高钢波纹管涵的强度和刚度，结构更加稳定、安全。