等距螺旋锥齿轮MIM工艺参数多目标优化
2022-03-25刘赣华唐乃夫马瑞伍
刘赣华,唐乃夫,马瑞伍
(1.江西理工大学机电工程学院,江西 赣州 341000;2.深圳市密姆科技有限公司,广东 深圳 518100)
0 前言
小模数螺旋锥齿轮因其传动平稳、噪声小、强度高等优点被广泛用于电动工具、机械仪表、汽车、家电、办公设备等需要相交轴传动的领域[1-2]。现阶段螺旋锥齿轮传动中的小轮由于节锥角较小而无法顺利脱模,不能采用精锻或注射成型的方式批量化生产,需要在5轴联动加工中心或专用机床上进行机加工生产,这使得生产成本高且制造周期长。对于小模数螺旋锥齿轮的加工,目前国内提出小轮采用双面法铣齿加工、大轮采用模具法成型加工(注:这种模具成型仅是一种近似齿形,适用于精度要求不高的传动类型),仅实现了大轮批量化生产,小轮仍需成本较高的机加工生产[3-4]。等距螺旋锥齿轮作为一种新型锥齿轮,采用球面渐开线作为齿廓线,等距圆锥螺旋线作为齿向线,其螺旋齿面具有法向等距的特点,可以通过旋转出模的方式实现与模具分离,适用于MIM以实现螺旋锥齿轮批量化生产。
MIM工艺是塑料成型工艺学、高分子化学、粉末冶金工艺学和金属材料学等多学科相结合而形成的一种零部件新型近净成型技术,此成型技术可以应用于几何形状复杂、组织结构均匀、精密度高以及具有特殊要求的小型零件(0.2~200 g)[5-7]。MIM制件在成型过程中,由于工艺参数和结构的影响,制件会产生不均匀分布的体积收缩,而分布不均匀的体积收缩会导致制件出现翘曲以及脱模变形[8]。此外,喂料在流入模具时会与内壁产生摩擦力,使得喂料在模具通道内产生高剪切速率梯度,靠近内壁的剪切速率最大,中心区域的剪切速率最小,导致内壁附近的粉末浓度较低,通道中心区域的粉末浓度较高,通道内部粉末浓度分布不均匀,而不均匀的粉末浓度会使得制件表面形成黑线[9-11]。因此研究体积收缩和粉末浓度分布的均匀性是必不可少的,以确保成型制件满足所需的尺寸精度和表面质量要求。
国内外一些学者研究了注射成型过程的多目标参数优化,Zhao等[12]总结了已有的优化方法,Tian等[13]采用非支配排序遗传算法(NSGA-II)对产品质量和能量消耗进行优化,Zhang等[14]采用拉丁超立方采样、神经网络和多目标粒子群算法优化成型过程的翘曲、峰值应力和锁模力指标。然而,目前很少有学者研究MIM制件的体积收缩分布和粉末浓度分布的多目标工艺参数优化。
基于以上讨论,本文创新性将MIM工艺用于等距螺旋锥齿轮的加工,以实现螺旋锥齿轮的批量化生产,并经过脱模试验,验证了等距螺旋锥齿轮小轮可以实现旋转脱模。由于等距螺旋锥齿轮结构较复杂,对制件单一目标进行优化难以满足质量要求,于是本文基于BP神经网络与NSGA-II算法对MIM等距螺旋锥齿轮制件的体积收缩分布和粉末浓度分布进行多目标工艺参数优化,得到最优工艺参数,以确保其尺寸精度和表面质量要求。
1 等距螺旋锥齿轮MIM工艺试制
1.1 等距螺旋锥齿轮三维模型
根据实际使用情况和齿轮的特性,参考格里森弧齿锥齿轮的相关参数,并查阅相关文献[15],设计了一对小模数等距螺旋锥齿轮,相关几何参数如表1所示。
本文采用的等距螺旋锥齿轮,齿廓线采用球面渐开线,齿向线采用等距圆锥螺旋线,根据球面渐开线和等距圆锥螺旋线的参数方程,并利用坐标变换推导出齿面方程[16-18]。在软件Matlab中编程计算出齿面离散点,如图1所示;再将离散点坐标导入软件UG中进行逆向建模拟合出齿面,如图2(a)所示;接着建立轮齿的顶锥面、根锥面、前锥面和背锥面,再通过修剪、缝合、阵列等命令完成等距螺旋锥齿轮小轮的精确建模,保证了后续小轮的电极加工与MIM仿真分析的准确性,模型如图2(b)所示。
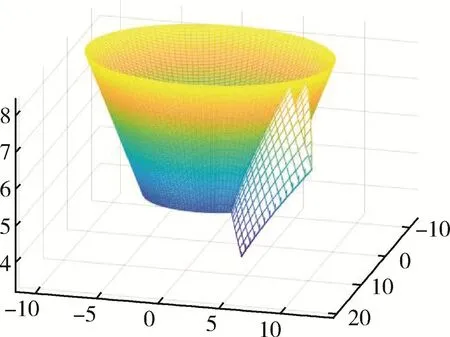
图1 等距螺旋锥齿轮齿面Fig.1 Tooth surface of the equidistant spiral bevel gear

图2 等距螺旋锥齿轮模型Fig.2 Model of the equidistant spiral bevel gear
1.2 试模验证
基于等距螺旋锥齿轮的三维模型,在五轴联动加工中心完成齿轮的电极加工,并在精密火花机上放电出对应的型腔,如图3(a)所示。参考有限元分析结果和MIM制件实际生产加工过程,设计MIM等距螺旋锥齿轮模具,在注射机上完成等距螺旋锥齿轮的金属粉末注射成型(采用Fe-8Ni材料),产品如图3(b)所示。验证了等距螺旋锥齿轮小轮可以旋转脱模,MIM工艺是可以用于等距螺旋锥齿轮的批量化生产。

图3 齿轮产品照片Fig.3 Physical photos of grears
2 正交试验设计及MIM仿真分析
2.1 有限元模型的建立
考虑工程实际应用,以及Moldex3D仿真软件的材料库,本文采用合金粉末作为金属粉末、聚丙烯(PP)作为黏结剂进行后续分析。材料的有关信息如表2所示。

表2 金属粉末与黏结剂的材料信息Tab.2 Material information of metal powder and binder
Moldex3D是很成熟且计算准确的注射成型仿真分析软件,国内外有很多学者使用该软件进行注射成型仿真分析[19-20]。由于齿轮轴壁厚均匀,质量较好控制,而螺旋锥齿轮齿形较复杂且壁厚不均匀,质量难以控制,所以本文仅对齿形部分进行MIM工艺优化。将等距螺旋锥齿轮三维模型导入MIM仿真软件Moldex3D中,设计浇口、流道系统、冷却系统并划分网格,随后选定合适的复合材料以及工艺参数,对其进行冷却、充填、保压的注射成型仿真分析,模型的网格与流道系统如图4所示。
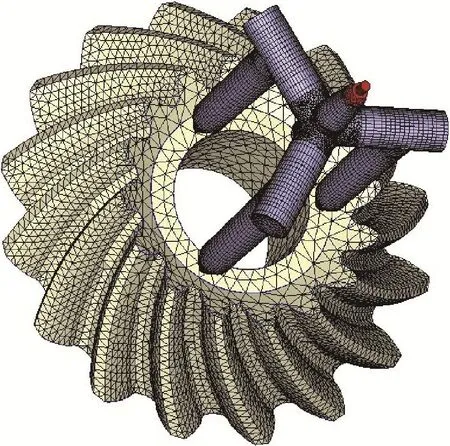
图4 模型的浇注系统Fig.4 Gating system of the model
2.2 正交试验设计
结合实际工作情况与相关文献资料,本文的MIM工艺参数优化考虑了5个影响因子,即充填时间、浇口直径、模具温度、熔体温度和保压压力。模具温度、熔体温度的工艺参数取值范围由Moldex3D软件库中所选复合材料的推荐值,其他因素的参数值则由实际注射成型加工与大量的前期模拟分析的结果来综合确定,每个因子设计了5个水平值,如表3所示。
基于Minitab软件,设计了L25(55)的正交试验,将表3的因子与水平值和正交表对应,生成25组试验。利用Moldex3D软件对25组试验参数进行注射成型仿真分析,得出所研究的体积收缩率与粉末浓度的平均值(μ)、标准差(σ),如表4所示。
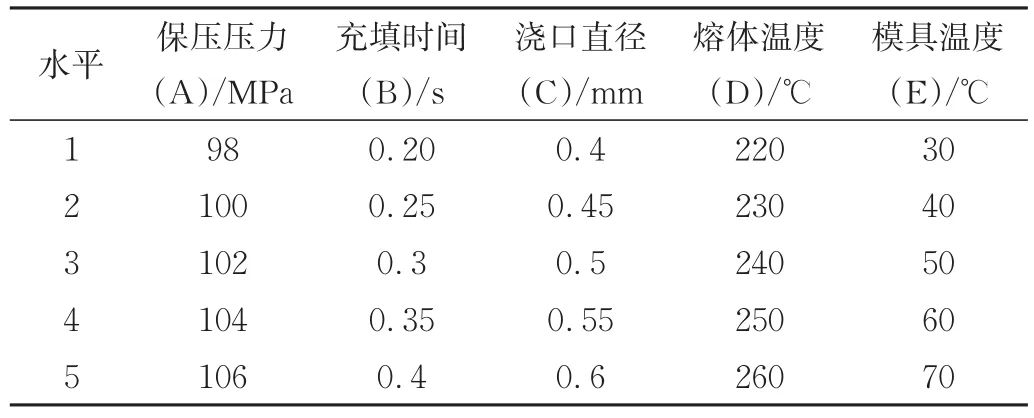
表3 试验因子与水平值Tab.3 Test factor and level value
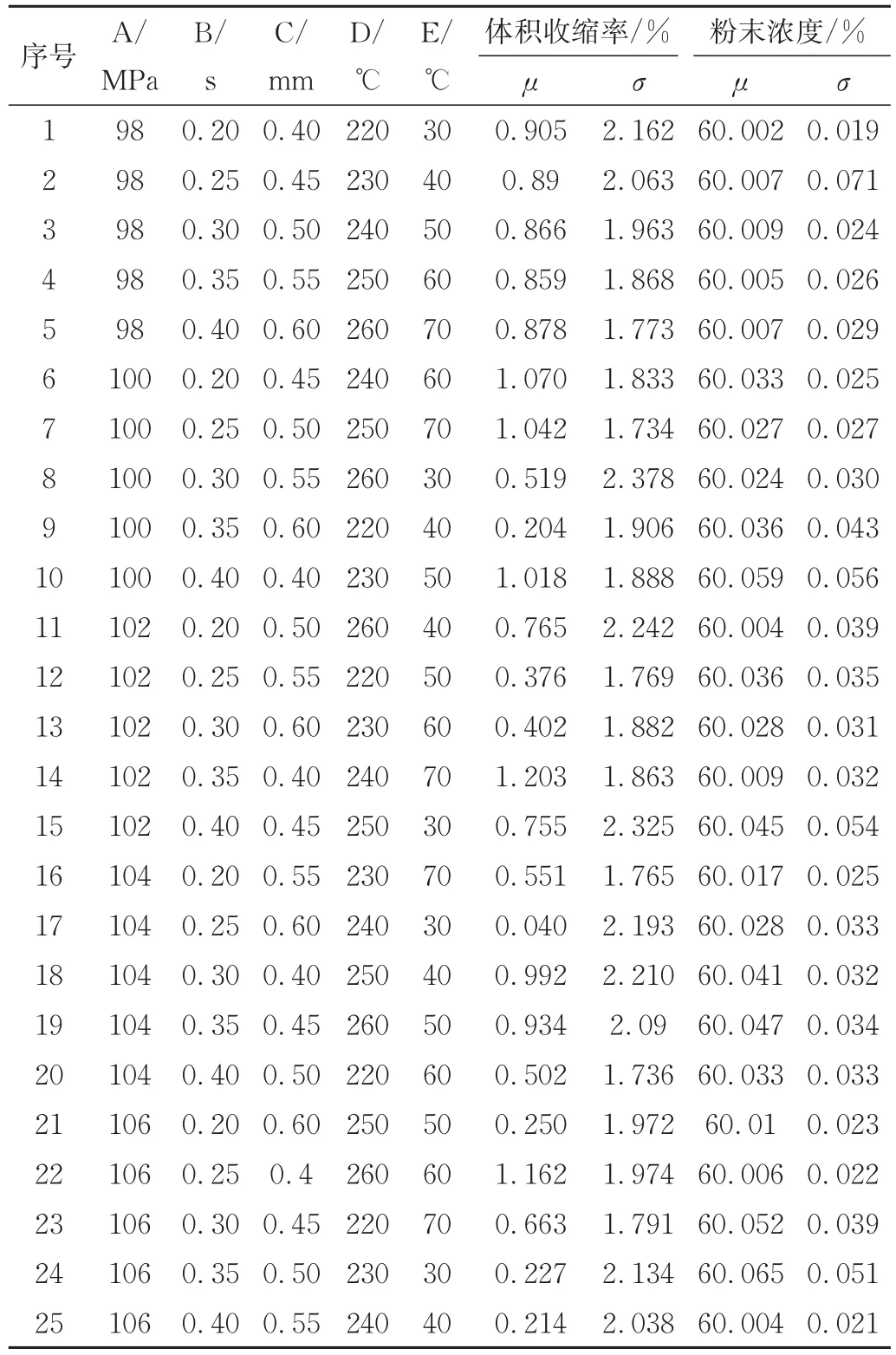
表4 体积收缩率与粉末浓度分布Tab.4 Volume shrinkage and powder concentration distribution
对于正交实验结果,第7组试验的体积收缩率标准差最低,为1.734%,仿真结果如图5(a)所示;第1组试验的粉末浓度标准差最低,为0.019%,仿真结果如图5(b)所示。
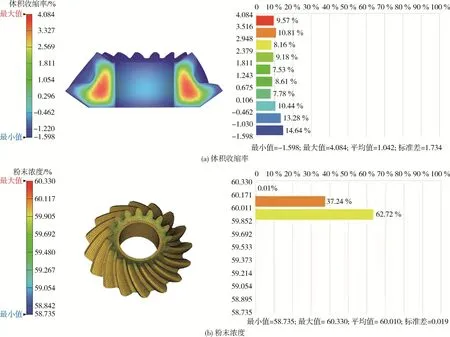
图5 仿真结果Fig.5 Simulation results
2.3 数据分析
对于25组正交试验结果,为了便于分析各参数因子对响应的影响情况,本文对其进行了均值分析、极差分析[21]。工艺参数对体积收缩率标准差的极差分析如表5所示,L1~L5为各因子在5个水平值时的体积收缩率标准差的均值,R为各因子均值的极差。分析结果表明保压压力、充填时间、浇口直径、熔体温度与体积收缩率标准差是非线性关系,而模具温度与体积收缩率标准差是负相关,且各工艺参数对体积收缩率标准差的影响程度由大到小依次为:模具温度、充填时间、保压压力、熔体温度、浇口直径。
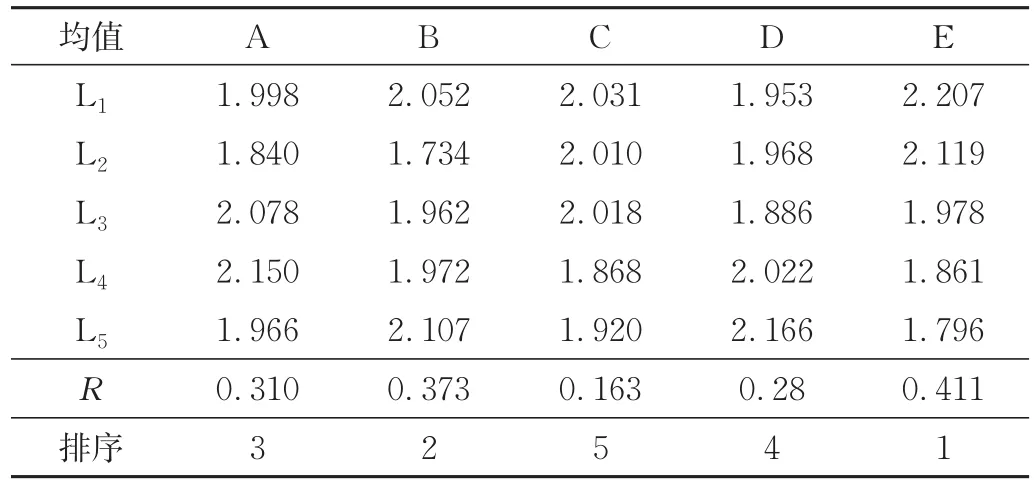
表5 工艺参数对体积收缩率标准差的均值和极差Tab.5 Simulation results mean and range of process parameters on standard deviation of volume shrinkage
工艺参数对粉末浓度标准差的极差分析见表6,L1~L5为各因子在5个水平值时的粉末浓度标准差的均值;R为各因子均值的极差。分析结果表明保压压力、浇口直径、熔体温度、模具温度与粉末浓度标准差是非线性关系,而充填时间与其为正相关,且各工艺参数对粉末浓度标准差的影响程度由大到小依次为:充填时间、熔体温度、保压压力、模具温度、浇口直径。
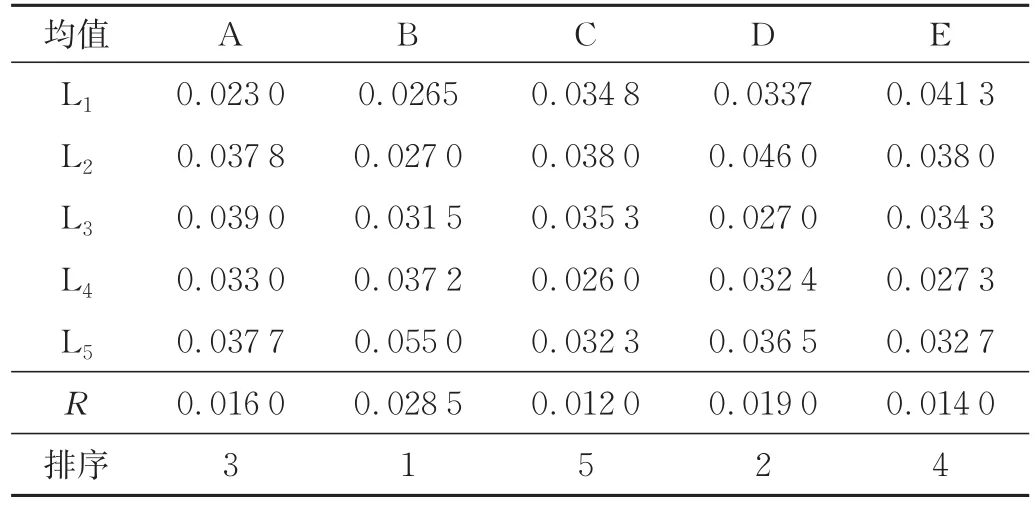
表6 工艺参数对粉末浓度标准差的均值和极差Tab.6 Mean and range of process parameters on the standard deviation of powder concentration
3 MIM工艺参数多目标优化
在本文中,体积收缩分布的均匀性用体积收缩率标准差来量化,体积收缩率标准差越小,各部位体积收缩的程度越接近,则制件的翘曲和变形量越小,因此为了控制制件的翘曲和变形量,体积收缩率标准差应尽可能小;粉末浓度分布的均匀性用粉末浓度标准差来量化,粉末浓度标准差越小,表明粉末浓度分散度越小,粉末浓度分布越均匀,则制件表面的黑线效应越不容易产生,因此为了控制制件表面的黑线效应,粉末浓度标准差应尽可能小。
本文对MIM等距螺旋锥齿轮的体积收缩率标准差、粉末浓度标准差进行工艺参数多目标优化,先基于正交试验的数据样本进行BP神经网络的训练与测试,再用NSGA-II遗传算法进行函数极值寻优。
3.1 BP神经网络模型的建立
BP神经网络具有输入层、隐含层和输出层,当输入层节点数为m,输出层节点数为n,那么BP神经网络就是m个自变量到n个因变量的映射关系,而隐含层节点数h可根据经验公式来初步确定:h=2m+1[22]。有关研究表明该映射一般通过3层BP神经网络来逼近,增加层数可以提高网络精度,但也会使得网络复杂性提高从而数据训练效率较低[23]。
将正交试验表4中的25组数据随机选取16组作为训练样本,随机选取1、3、4、6、7、9、10、11、13、14、15、18、19、21、23、24组,以完成对BP神经网络模型的训练,剩余9组数据则作为测试样本来检验模型的准确性。依据式(1)对数据进行归一化处理消除其量纲的影响,将所有数据归一化处理到区间[-1,1]。保压压力、充填时间、浇口直径、熔体温度、模具温度的参数值作为BP神经网络模型的输入,则输入节点数为5,而体积收缩率标准差和粉末浓度标准差作为模型的输出,输出节点数为2。
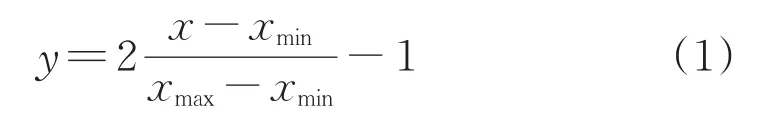
式中x——归一化处理前的数据值
xmax——归一化处理前的数据最大值
xmin——归一化处理前的数据最小值
y——归一化处理后的值
基于软件Matlab,调用神经网络工具箱对数据进行训练,为了提高模型收敛速度,本文采用Levenberg-Marquardt算法来改进BP神经网络。对于本文的BP神经网络,训练函数采用trainlm,输入层到隐含层的传递函数采用tansig,而隐含层到输出层的传递函数为purelin。经过模型调试,隐含层节点数h选择11,模型的目标误差设定为10-5,学习效率为0.01,最大迭代次数设定为5 000。用测试样本数据对训练好的模型进行误差检测,模型预测值及其与Moldex3D仿真值的误差如图6所示。
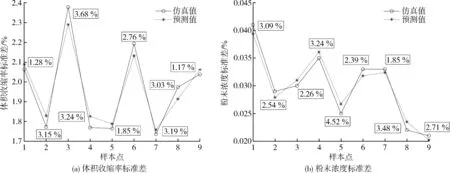
图6 模型进行误差检测结果Fig.6 Error detection results of the model
体积收缩率标准差的平均误差为2.59%,最大误差为3.68%,而粉末浓度分布标准差的平均误差为2.9%,最大误差为4.52%。BP神经网络模型最大误差均小于5%,证明BP神经网络模型预测值与Moldex3D软件的仿真值误差较小,模型训练完成,且准确性足够。
3.2 遗传算法多目标优化
本文以体积收缩率标准差、粉末浓度标准差最小值为目标,约束条件为保压压力、充填时间、浇口直径、熔体温度、模具温度的参数范围,BP神经网络预测模型作为多目标算法NSGA-II的适应度函数,经过选择、交叉和变异操作得到体积收缩率标准差、粉末浓度标准差的最小值以及对应的工艺参数。建立体积收缩率标准差f1、粉末浓度标准差f2的数学优化模型:minf1(x1,x2,x3,x4,x5),minf2(x1,x2,x3,x4,x5),此时约束条件为:98 MPa ≤x1≤106 MPa,0.2 s≤x2≤0.4 s,0.4 mm≤x3≤0.6 mm,220 ℃ ≤x4≤260 ℃ ,30℃≤x5≤70℃。遗传算法中种群规模设为300,交叉概率为0.8,变异概率为0.05,迭代次数为200。
以体积收缩率标准差小于1.62%、粉末浓度标准差小于0.018%作为条件进行筛选,得出如图7所示的有13个解的pareto前沿。两个优化目标之间有着一定的交互作用,无法同时达到单个目标的最小值,而本研究中体积收缩率标准差、粉末浓度标准差同等重要,因此权重均为1。据此确定的pareto最优解为:保压压力99.183 MPa、充填时间0.241 s、浇口直径0.548 mm、熔体温度240.702℃、模具温度63.981℃,并且此时体积收缩率标准差为1.532%、粉末浓度标准差为0.013 5%。
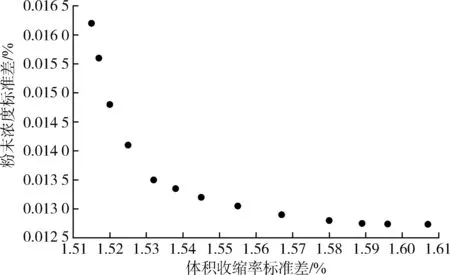
图7 Pareto最优解Fig.7 Pareto optimal solution
3.3 仿真验证及结果分析
对多目标优化得到的MIM工艺参数,进行金属粉末注射成型仿真分析,得到优化后的体积收缩分布和粉末浓度分布如图8所示,此时体积收缩率标准差为1.491%、粉末浓度标准差为0.013%,与多目标优化的预测值误差分别为2.7%、3.8%,均小于5%,表明本文的多目标优化模型是准确的。
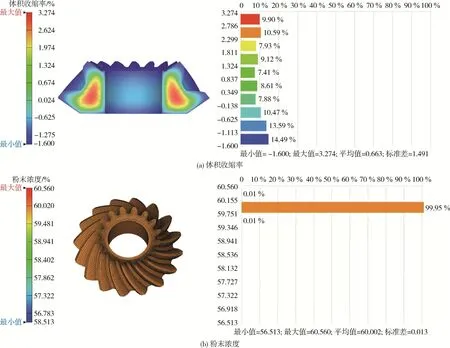
图8 仿真结果Fig.8 Simulation results
如图9(a)所示,曲线1为正交试验最小体积收缩率,曲线2为多目标优化之后的体积收缩率,平均体积收缩率由1.042%降低到0.663%,更接近于标准目标值零,而体积收缩率标准差由1.734%降低到1.491%,标准差降低了14%。如图9(b)所示,曲线1为正交试验最小粉末浓度,曲线2为多目标优化之后的粉末浓度,平均粉末浓度由60.01%降低到60.002%,更接近于标准目标值60%,而粉末浓度标准差由0.019%降低到0.013%,标准差降低了31.6%。根据图中正态分布曲线和数据可以得出本文有效改善了MIM等距螺旋锥齿轮的体积收缩和粉末浓度分布,极大提高了制件的质量。
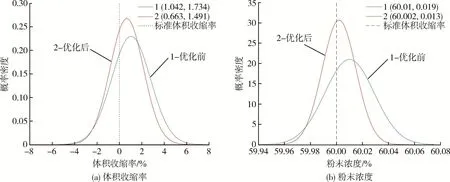
图9 体积收缩率和粉末浓度的正态分布曲线Fig.9 Normal distribution curve of volume shrinkage and powder concentration
4 结论
(1)对等距螺旋锥齿轮进行MIM工艺试制,通过旋转脱模方式注射成型出无明显翘曲且表面质量较好的样轮,验证了MIM工艺可以用于等距螺旋锥齿轮的批量化生产;
(2)基于正交试验和软件Moldex3D进行MIM仿真分析得到训练和测试BP神经网络的数据样本,选取保压压力、充填时间、浇口直径、熔体温度、模具温度作为输入层,以体积收缩率标准差、粉末浓度标准差作为输出层,建立BP神经网络模型,并将测试样本数据与模型预测数据做对比,得出BP神经网络模型是准确可靠的;
(3)基于NSGA-II算法对BP神经网络模型进行多目标寻优,得出最佳工艺参数为:保压压力99.183 MPa、充填时间0.241 s、浇口直径 0.548 mm、熔体温度240.702℃、模具温度63.981℃,并且此时体积收缩率标准差为1.532%、粉末浓度标准差为0.013 5%;将此最佳工艺参数输入Moldex3D软件中进行粉末注射成型仿真,仿真结果与pareto最优解误差小于5%,验证了本文的多目标优化模型是准确的;
(4)经过多目标优化,MIM等距螺旋锥齿轮的平均体积收缩率和平均粉末浓度分别由1.042%、60.01%降低到0.663%、60.002%,体积收缩率标准差与粉末浓度标准差分别下降了14%、31.6%,表明MIM工艺参数多目标优化有效提高了制件的体积收缩分布与粉末浓度分布的均匀性。
