一类组合恒等式问题的一般化与特殊化

广州大学数学与信息科学学院(510006);广州大学计算科技研究院(510006);广州市第二中学(510530)程汉波

1 问题提出

2 一般化

3 特殊化

特殊化通常是指一般化命题的特殊例子.波利亚也在《怎样解题》中阐述道:特殊化是从考虑一组给定的对象集合过渡到考虑该集合的一个较小的子集,或仅仅一个对象.特殊化可以通过具体的数字去进行代入,也可以指就“极端”的情况进行考虑,还包括作出具体的图形等.

应用以上一般化的命题1,利用特殊化的策略,可得如下几道文[3](以下例1、例2、例3)和文[4](以下例4、例5)中颇有难度的习(例)题.

以命题1 为背景的组合恒等式问题屡见不鲜.读者还可尝试寻找或命制出更多与此背景相关的组合恒等式,以感悟一般化的结论利用特殊化的策略在命题中的广泛使用.

4 再证一元次多项式的一个特性

尽管特殊化与一般化是在两个方向上进行的,但是,这两者在实际数学研究中又是密切相关的、相互依赖的.特殊化只有上升到一般的高度,我们可能更为深刻地认识和理解各个特殊的例子,才能更好地解决问题.

文[5]给出了一元n次多项式的如下一个特性,并利用高阶差分相关的知识进行了繁杂的证明,若利用命题1,该优美特性的简洁证明便是水到渠成.

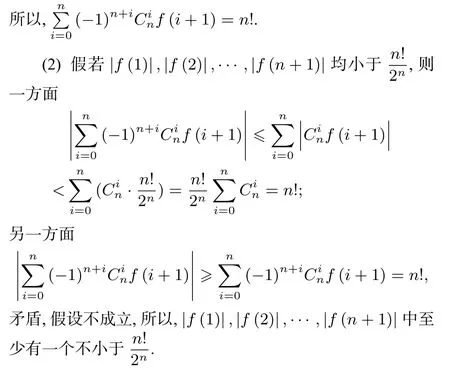
5 小结与反思

本文首先将特殊的两道中科大新生入学考试题和一道清华大学数学学科能力测试题(TACA)进行一般化,得到更加普遍和深刻的命题1,然后由一般化的命题1 又轻松地解决了文[3-4]中的五道习(例)题,即是将一般化的结果特殊化的体现.而且,在一般化与特殊化的“再创造”与“数学化”的过程中,简洁有力改良了文献[5]中有关一元n次多项式一条特性的证明过程.

由此可见,一般化、特殊化渗透于解题的全过程,协同解决数学问题.一般化与特殊化的螺旋过程中,能除去那些不必要的步骤,弄清问题的关键所在,使思路明晰起来,抓住问题的本质,给出一些简单、漂亮的解法和变式训练.这样,我们在学习数学知识的同时收获了学习知识的方法、也收获了愉悦充实的心情.

正如波利亚把一般化、特殊化和类比并列地称为“获得发现的伟大源泉”.英国著名数学家梅森集中研究了数学中的特殊化和一般化方法及其在解题中的作用后认为:特殊化与一般化正是数学思维的核心,同时也是怎样解题的关键.