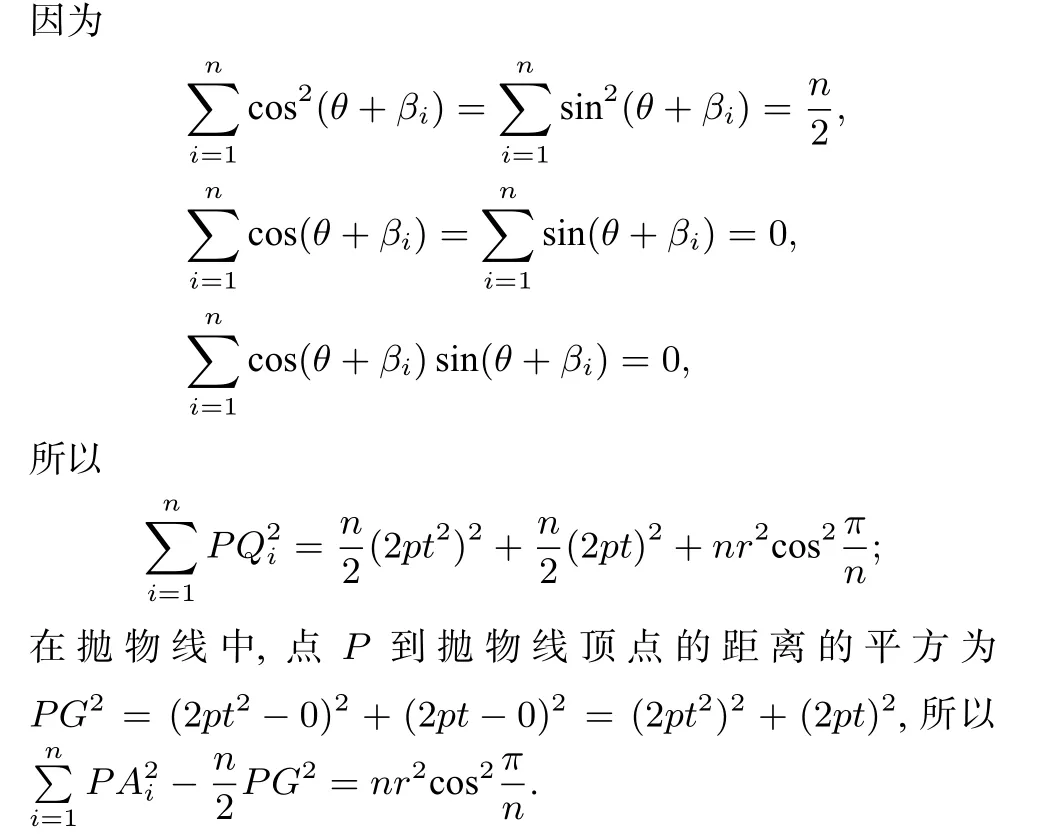正多边形同心圆锥曲线的两个性质

广东省广州市花都区新华培新学校(510800)洪鹏花

广东省广州市花都区赤坭镇赤坭圩小学(510830)李思根

文[1]研究了正多边形的同心圆(即圆心在正多边形中心的圆)的两个性质:(1)正多边形同心圆上的任意一点到各顶点距离的平方和是定值;(2)正多边形同心圆上任意一点到各边距离的平方和是定值.

文[2]推广了文[1]的结论,得到了正多边形的同心椭圆(即椭圆中心在正多边形中心的椭圆)的两个性质:(1)设G为正n边形的中心,则以G为中心的椭圆上任意一点到正n边形的各顶点的距离的平方和与该点到椭圆两焦点距离的乘积的n倍之和为定值;(2)设G为正边形的中心,则以G为中心的椭圆上任意一点到正n边形的各边所在直线的距离的平方和与该点到椭圆两焦点距离的乘积的倍之和为定值.

圆锥曲线包括:圆、椭圆、双曲线、抛物线.圆与椭圆具有以上两个性质,本文把以上两个性质推广到双曲线和抛物线.

正多边形的同心双曲线,即双曲线中心在正多边形中心的双曲线;正多边形的同心抛物线,即抛物线顶点在正多边形中心的抛物线,以上同心圆、同心椭圆、同心双曲线、同心抛物线统称为正多边形同心圆锥曲线.

定理1设G为正n边形的中心,则以G为中心的双曲线上任意一点P到正n边形的各顶点的距离的平方和与点P到双曲线两焦点距离的乘积的n倍之差为定值n(a2-b2+r2),其中a,b分别为双曲线的实半轴和虚半轴的长度,r为正n边形外接圆的半径.

证明如图1所示,点G为正多边形A1A2···An和双曲线C:的中心,点P是双曲线C上的任意一点,如图1 以G为原点建立平面直角坐标系.

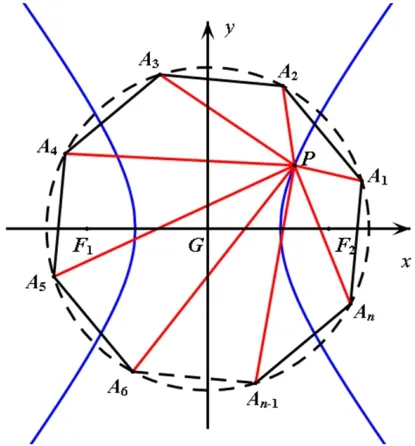
图1

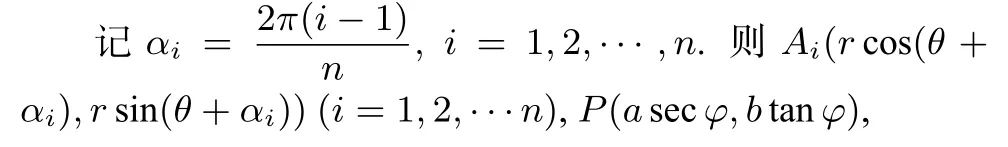
定理2设G为正n边形的中心,则以G为中心的抛物线上任意一点到正n边形的各顶点的距离的平方和与该点到抛物线顶点距离的平方的n倍之差为定值nr2,其中r为正n边形外接圆的半径.

证明如图2所示,点G为正多边形A1A···An和抛物线C:y2= 2px(p ＞0)的中心,点P是抛物线C上的任意一点,如图2 以G为中心建立平面直角坐标系,设正多边形外接圆半径为r.

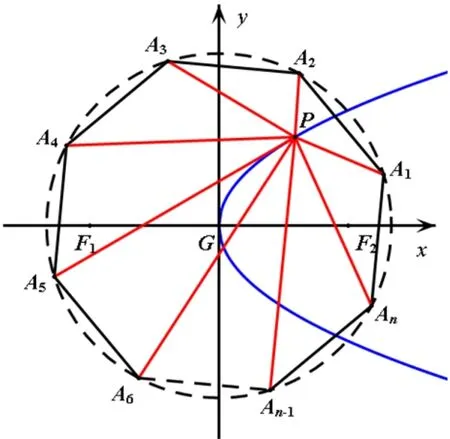
图2