用斯坦纳定理求解异面直线夹角的适用范围

云南师范大学数学学院(650000)崔永宏 刘丹 马绍文

1 问题提出

空间中两条异面直线夹角问题一直是高考的热点话题,如刚刚结束的2021年高考全国乙卷理科第5 题(文科第9题).这种题目往往会有两种解答过程,综合几何法与向量坐标法.追溯历史缘由,欧几里得的《几何原本》与阿波罗尼奥斯的《圆锥曲线论》采用图形平移、添补、拆分等技巧性的几何方法将几何学的基本性质与定理几乎网络殆尽,以至于20个世纪的后人在这方面增添的新内容寥寥无几[1].直到17世纪,笛卡尔用代数的方法重新研究几何图形,几何学发展进入一个新的阶段,并诞生射影几何、微分几何等研究领域.因此,《普通高中数学课程标准(2017年版)》指出学生在学习平面向量的基础上,运用向量的方法研究空间基本图形的位置关系和度量关系,体会向量方法和综合几何法的共性和差异[2].

对于一些简单的规则几何模型(如2015年高考浙江卷理科第13 题),采用综合几何法,通过图形平移、添补、拆分,找到所求的角进而直接求出结果,会是比较好的选择.对于一些复杂的规则几何模型(如2017年高考天津卷理科第17题),此时直接找两条异面直线所成的角并不是一件容易的事情,往往需要建立空间坐标系,借助空间向量解决问题.有没有其他方法解决空间中两条异面直线所成夹角问题?

2 斯坦纳定理

斯坦纳定理在四面体ABCD中,异面直线AB与CD所成夹角记为则

需要说明的几点:

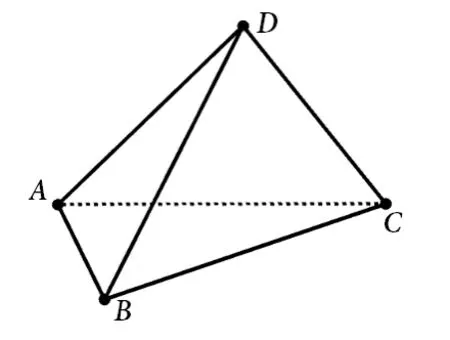
图1

1.这个定理有的文献中也称作空间余弦定理[3],但是并不是余弦定理由二维平面向三维空间推广得到的产物,二维平面的线段推广到三维空间应该是一个平面,事实上,余弦定理的推广形式应该是四面体余弦定理形式[4].因此,防止引起误会,我们采用斯坦纳定理的说法[5].

2.公式的记忆比较简单,分母的位置是所求的两条直线,如图2,不妨记A1A2,A3A4,分子则是外和2+ 内和2-交叉2-交叉2的绝对值,即

图2

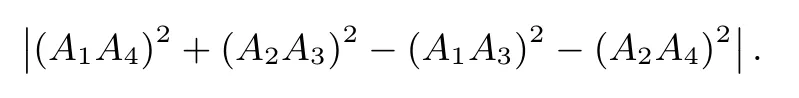
3 模型初探

例1(2015年高考广东卷理科第18 题第3 问)如图3,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.点E是CD边的中点,点F,G分别在线段AB,BC上,且AF= 2FB,CG= 2GB.求直线PA与直线FG所成角的余弦值.

图3

从这个例题的解法可以看出:

1.本题具有一般性,能完整体现斯坦纳定理在解决问题时的解题过程与需要注意的细节.解题步骤如下:

(1)确定所求夹角的两条异面直线;(2)依据确定两条直线的四个点,补全以该四点为顶点的四面体;(3)分别求出四面体的六条边长(很多时候只需要求三条,其他的题目会给出);(4)代入公式直接计算.

需要注意的细节:(1)分子的位置带有绝对值;(2)应用勾股定理求解四面体边长特别需要重视截面图.

2.对本例而言,斯坦纳定理不是最好的选择,原因有两个:(1)就解题过程而言,核心步骤是如何求四面体的边长,即空间几何体平面化,这很好的考察答题者的正确画出空间体截面图能力,空间想象能力,对学生直观想象素养提出较高的要求,可以说定理自身固有一定难度;这个固有的难度比例题本身的难度还要大.(2)另一个原因,上面我们也提到过,这是一个简单且规则的图形,便于找到异面直线所成的角或者建立直角坐标系.当不满足上述情况,例如让平面动起来,这时斯坦纳定理才会凸显出它的价值.

4 举例说明

例2(2016年高考浙江卷文科第14 题)如图4,已知平面四边形ABCD,AB=BC= 3,CD= 1,AD=沿直线AC将ΔACD翻折成ΔACD′,直线AC与BD′所成的角的余弦的最大值是____.

图4

注记这是一道异面直线夹角试题,不同的是几何图形是移动的.采用向量坐标法时,难点在如何求得动点D′的坐标.这需要明确点D′的运动轨迹,如果判断不出D′的运动轨迹是圆,这个方法是没有办法进行下去的.采用综合几何法,难点在如何将AC与BD′平移到同一个平面.为此,解法三添加了三个辅助点,七条辅助线,使得解题过程难点重重.上述两种方法确实可行,但对中学生来讲,难度太大,已经远远超出斯坦纳定理自身所带的难度.斯坦纳定理应用到本题恰到好处,先用定理确定cosθ由BD′唯一决定,进而问题转化为BD′的范围问题.cosθ取最大值,需要BD′取最小值,显而易见的是BD′随着ΔACD′翻折逐渐变小,临界点在两平面重合时,判断此时BD的值,问题得到解决.

5 举一反例

是否对动点轨迹模型下的两条异面直线夹角问题,斯坦纳定理都会有这样的效果呢?

例4(2015年高考四川卷理科第14 题)如图5,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点.设异面直线EM与AF所成角为θ,则cosθ的最大值为____.

图5

注记这是一道中规中矩的向量坐标法求解异面直线夹角的试题.尽管是动点轨迹模型,但动点的轨迹清晰可见,动点的坐标在空间直角坐标系下一目了然.此时,强行使用斯坦纳定理会使得运算难度加大,变成为了使用方法而使用方法.综合几何法给出的过程最少,看似简单,但是显然MF⊥AF的表述,不是刻意思考,又有几人能真正做到.

6 总结

方法虽好,应以注意使用的范围为前提,强行为了方法而方法,只会让数学变得更复杂.数学教育者研究解题方法是为了解决数学问题,让数学变得更易于理解.当你决定应用斯坦纳定理解决两异面直线夹角问题时,那一定是向量坐标法与综合几何法都束手无策的前提下.因为尽管定理的表述形式很简洁也便于记忆,但是边长的计算却有相当难度,以2014年高考全国Ⅱ卷理科第11 题为例,读者可自行验证.

题目(2014年高考全国Ⅱ卷理科第11 题)直三棱柱ABC - A1B1C1中,∠BCA= 90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( ).