Faster Approximation for Rectilinear Bottleneck Steiner Tree Problem

，

( College of Computer Science, South-Central University for Nationalities, Wuhan 430074, China )



Faster Approximation for Rectilinear Bottleneck Steiner Tree Problem

LiZimao，LiXiaodan

( College of Computer Science, South-Central University for Nationalities, Wuhan 430074, China )

Bottleneck Steiner tree problem asks to find a Steiner tree fornterminals with at mostkSteiner points such that the length of the longest edge in the tree is minimized. The problem has applications in VLSI routing, wireless communication networks and phylogenetic tree reconstruction. Du and Wang showed that the rectilinear bottleneck Steiner problem is NP-hard and cannot be approximated within performance ratio 2 in polynomial time, and provided a 2-approximation algorithm running in actual time O(nlog2n+kn+k2). In this paper we improve the algorithm′s time complexity to O(nlog2n+klog2n) and armotized O(nlog2n+klog2n), by introducing the binary heap and Fibonacci heap respectively. The improvement can be directly applied to their Euclidean bottleneck Steiner tree problem′s 2-approximation algorithm.

bottleneck Steiner tree; approximation algorithm; performance ratio; wireless communication networks

1　Introduction

In the 1990s, along with the conquest of a series of famous conjectures, the traditional Steiner tree problem[1]attracted the scientists′ considerable attention and interests from both theoretical point of view and its applicability and once occupied a central place in the emerging theory of approximation algorithms.

Given a weighted graphG=(V,E;W) and a subsetS⊂Vof required vertices, the traditional Steiner tree problem asks a least weight tree spanningS. The tree may use additional points(called Steiner points) inV-S. We call such a tree a Steiner tree. The problem is MAX-SNP hard even when the edge weights are only 1 or 2[2]. For the Steiner tree problem in Euclidean plane, it is still NP-hard and there is a polynomial-time approximation scheme (PTAS) for Euclidean Steiner trees[3].

New applications of Steiner tree problem in VLSI routing[4], wireless communications[5]and phylogenetic tree reconstruction in biology[6]have been found and studied deeply. These applications triggered the study of variations of the traditional Steiner tree problem. Algorithms for the two variations, the bottleneck Steiner tree problem[7-12]and the Steiner tree problem with minimum number of Steiner points and bounded edge-length[9, 13-15], have been studied widely and deeply.

In this paper, we consider the bottleneck Steiner tree problem, which is defined as follows: given a setP={p1,p2,…,pn} ofnterminals and a positive integerk, we want to find a Steiner tree with at mostkSteiner points such that the length of the longest edges in the tree is minimized.

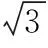
In this paper we consider the rectilinear bottleneck Steiner tree problem. D.-Z Du and L. Wang proved that the problem could not be approximated within ratio 2 in polynomial time and provided a 2-approximation algorithm which runs in O(nlog2n+kn+k2) time but not they mentioned O(nlog2n+klog2n)[7]. The performance ratio is best possible and any improvement of the ratio will lead to P=NP. By introducing two advanced data structures, the binary heap and the Fibonacci heap, we can implement their algorithm′s time complexity to O(nlog2n+klog2n) and amortized O(nlog2n+klog2n), respectively.

2　 2-Approximation algorithm

D.-Z Du and L. Wang proved the existence of performance ratio 2 by constructing a steinerized spanning tree under the triangle inequality property in rectilinear plane. Their algorithm first construct a minimum spanning tree for the set ofnterminals inP, then they repeatedly add degree-2 Steiner point to long edges in the minimum spanning tree. We call such a tree a steinerized spanning tree. Their approximation algorithm was derived from the following two lemmas.

Lemma 1[7]: Given a set ofnterminalsPin the rectilinear plane, letTbe an optimal tree for the rectilinear bottleneck Steiner tree problem. Then there exists a steinerized spanning treeT′ forPwith the same number of Steiner points asTsuch that the length of the longest edges inT′ is at most twice that ofT.

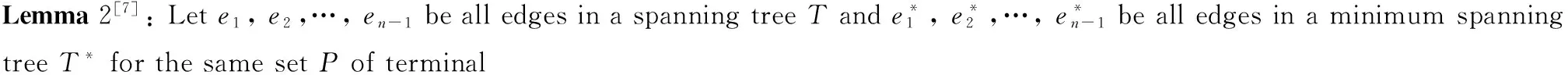
It follows immediately from Lemma 1 and 2 that when we use the same number of Steiner points to steinerize a spanning tree and a minimum spanning tree, the result from the latter has a longest edge of length not exceeding that from the former. That is, an optimal steinerized spanning tree can be found among steinerized minimum spanning trees. Since only degree-2 Steiner points are possibly adjacent, we only need to addkSteiner points to a minimum spanning tree in order to obtain an optimal steinerized spanning tree.

The idea is explained as follows: for each edgeei= (u,v) in the minimum spanning tree, if we addlidegree-2 Steiner points to it, then the length of the longest edge in the resulting path fromutovhas the minimum valuec(ei)/(li+1), wherec(ei) is the original length of edgeei. This minimum value is achieved when theliSteiner points divideeievenly. Denotel(ei) =c(ei)/(li+1).

At the beginning of the algorithm,l(ei)=c(ei). Each time a degree-2 Steiner point is added to the edgeeiwith the largestl(·) value. Aftereireceives one more degree-2 Steiner point,liis updated byli=li+1 andl(ei) is updated byc(ei)/(li+1) and the position of all the degree-2 Steiner points in the edgeeiis re-organized by dividingeievenly, Note thateiis defined in the rectilinear plane. The process is repeated untilkdegree-2 Steiner points are added.

Fig.1 shows D.-Z Du and L. Wang′s approximation algorithm with performance ratio 2[7].

Fig.1Du and Wang′s 2-approximation Algorithm for Rectilinear Bottleneck Steiner Tree Problem

图1Du和Wang的2-近似性能比网格空间瓶颈斯坦纳树算法

The algorithm′s time complexity is analyzed as below:

The first step can be implemented in O(nlog2n) time[18,19].

Step 2 uses linear time. Sorting in Step 3 takes O(nlog2n) time.

In each loop of Step 4-7, Step 4 and 5 use constant time to find the longest edge and updatel(·), Step 6 uses time linear to the number of Steiner points on that edge, and the step 7 of resettingei′s position needsO(n) time in the worst case.

As Step 4-7 only loopsktimes, the algorithm′s time complexity is O(nlog2n+kn+k2).

3　The faster algorithms

The most time consuming steps in the loop of the Du and Wang′s algorithm is Step 6 and 7, either linear to number of Steiner points or to the number of terminals in the worst case. First we find that moving step 6 in Fig.1 out of the loop as the final step can decrease the time of organization of Steiner points fromO(k2) toO(k) Then the step to find an edge with the largestl(·) and step to updatel(·) are frequently executed, together with Step 5 and 7 combined as a single step, which inspires us to use a priority queue to maintain all the edges associated with priorityl(·). The priority queue should support two operations efficiently: finding an edge with the largest priority and update an edge′s priority.

According to our case, a binary max-heap[20]is suitable to implement the priority queue. A binary max-heap is a heap data structure created using a binary tree with two additional constraints: (1) shape property, the tree is a complete binary tree; that is, all levels of the tree, except possibly the last one are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right; (2) heap property, the key at each node is greater than or equal to that of its children.

A max-heap supports the operations of a priority queue efficiently. We can construct a heap in linear time, and a max-heap returns a node with the largest key inO(1) time, and updates a node key in O(log2n) time. In fact, the introduce of max-heap also decreases the Step 7′s implementation time fromO(n) to O(log2n).

Now we can formulate our improved algorithms as below (See Fig.2).

It is easy to check that the time complexity of the above algorithm is O(nlog2n+klog2n). Obviously Step 2 only uses time linear ton. Constructing a max-heap in bottom-up fashion need onlyO(n) time. Step 4 runs in constant time because root of the heap indicating the edge with the largestl(·), while Step 5 uses O(log2n) to update an edge′s key, consider that the two steps loops forktimes, so Step 4 and Step 5 run in O(klog2n) in total. Step 7 can be implemented inO(n+k) time locating the position of added Steiner points.

Fig.2Faster algorithm for Rectilinear Bottleneck Steiner Tree Problem

图2网格空间瓶颈斯坦纳树快速算法

Remember that the first step runs in O(nlog2n), the improved algorithm′s time complexity is O(nlog2n+klog2n).

Theorem 1: There is an O(nlog2n+klog2n) time approximation algorithm with performance ratio 2 for the bottleneck Steiner tree problem in the rectilinear plane.

If we use a Fibonacci heap[20]to implement the priority queue, the algorithm can be implemented in amortized time O(nlog2n+klog2n). This is because heap construction takes onlyO(n) amortized time, while determining the edge with largest key and decreasing an edge′s key uses onlyO(1) and O(log2n) amortized time.

Simulation on the proposed algorithms shows that the advantages of our algorithm become more and more clear with the increasing number of Steiner points, and the Fibonacci heap-based implementation performs better than the binary heap-based when the number of terminals and Steiner points is big enough(See Fig.3～5).

Fig.3　Comparison of Implementation Time with Steiner Points the 50图3　斯坦纳点数目为50的实验结果比较

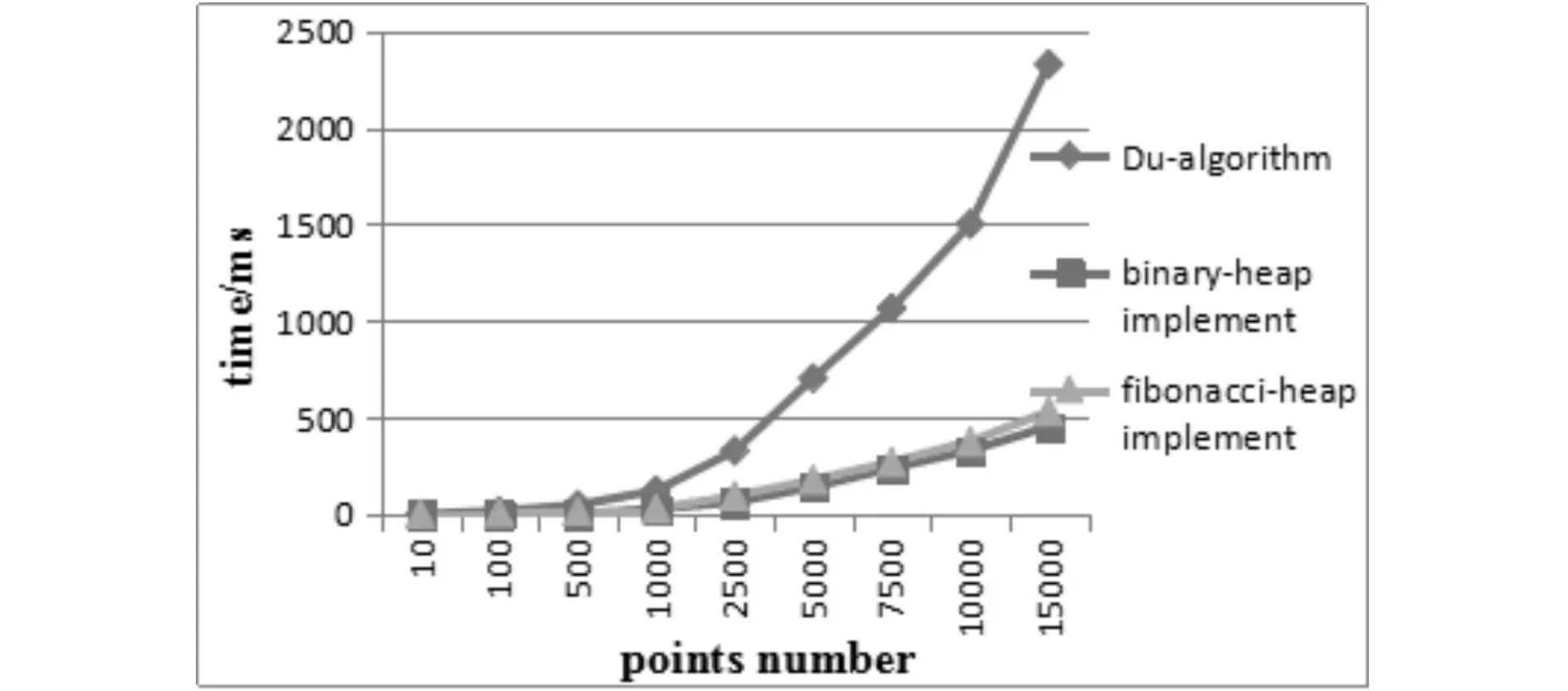
Fig.4　Comparison of Implementation Time with Steiner Points the 500图4 斯坦纳点数目为500的实验结果比较

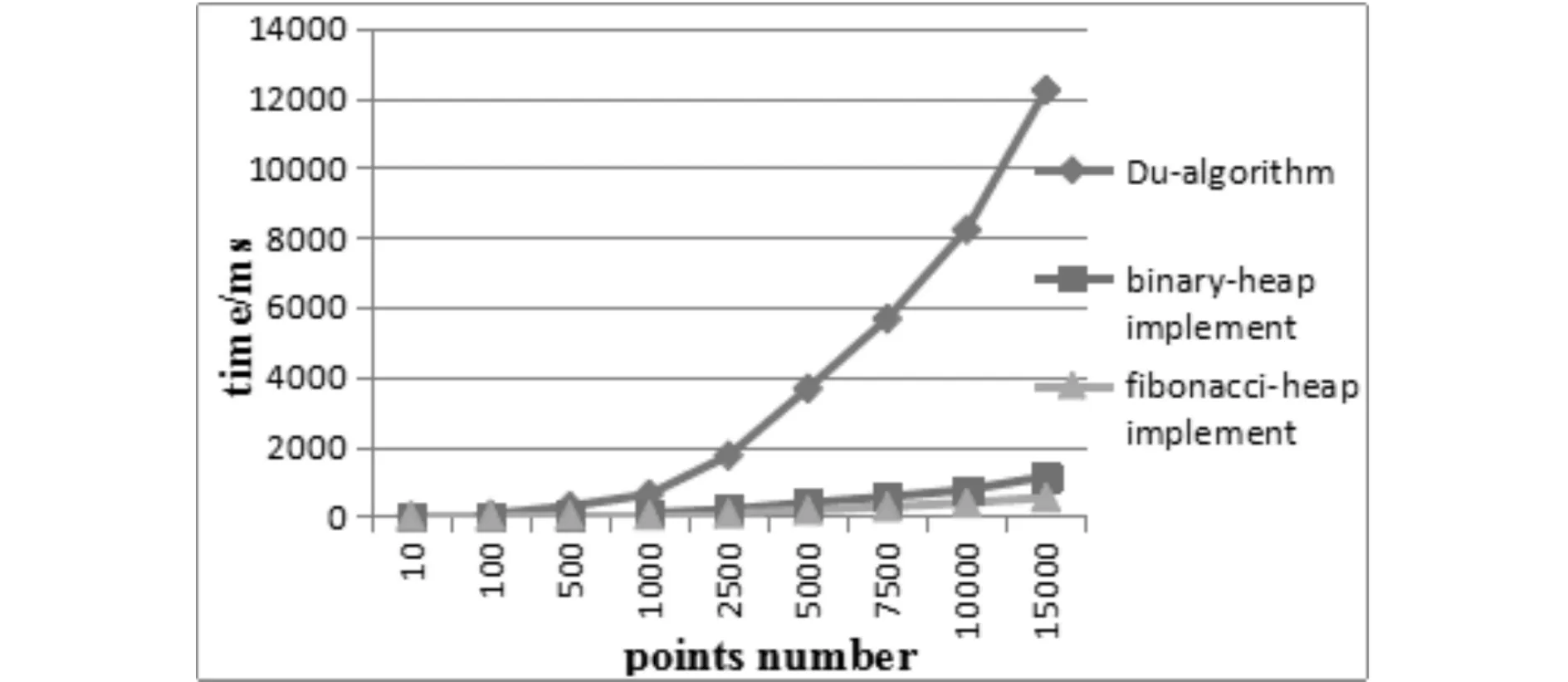
Fig.5　Comparison of Implementation Time with Steiner Points the 3000图5 斯坦纳点数目为3000的实验结果比较

4　Conclusion

We mainly considered the rectilinear bottleneck Steiner tree problem. The problem asks to find a Steiner tree withnfixed terminal nodes in the rectilinear plane and up tokSteiner nodes such that the length of the longest edge in the tree is minimized. We first introduced D.-Z Du and L. Wang′s approximation algorithm with performance ratio 2. Then by introducing binary heap and Fibonacci heap, together with a slightly adjustment of their algorithm, we improve their algorithm′s time complexity to O(nlog2n+klog2n) and amortized O(nlog2n+klog2n), respectively. Simulations are conducted to indicate the effectiveness and efficiency of our improved implementation and the Fibonacci-heap-based algorithm′s complexity makes such an improvement primarily of theoretical value.

An observation is that our improvements can be directly applied to Du and Wang′s polynomial approximation algorithm with performance ratio 2 for the Euclidean bottleneck Steiner tree problem.

As an application, the algorithm can be used to improve the lifetime of wireless networks by minimizing the length of the longest edge in the interconnecting tree by deploying additional relay nodes at specific locations.

[1]Garey M R, Graham R L, Johnson D S. The Complexity of Computing Steiner Minimal Trees[J]. SIAM Journal on Applied Mathematics, 1977, 32(4): 835-859.

[2]Bern M, Plassmann P. The Steiner Problem with Edge Lengths 1 and 2[J]. Information Processing Letters, 1989, 32(4): 171-176.

[3]Arora S. Polynomial Time Approximation Scheme for Euclidean TSP and Other Geometric Problems[C]//Anonymous. Proceedings of the 37th Annual Symposium on Foundations of Computer Science. Burlington: CA, 1996: 2-11.

[4]Kahng A,Robins G. On Optimal Interconnections for VLSI[M]. Springer: Springer Science & Business Media, 1995.

[5]Caldwell A, Kahng A, Mantik S, et al. On Wirelength Estimations for Row-based Placement[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1999, 18(9): 1265-1278.

[6]Hwang F K, Richards D S, Winter P. The Steiner Tree Problem[M]. North-Holland:Elsevier, 1992.

[7]Wang L, Du D-Z. Approximations for a Bottleneck Steiner Tree Problem[J]. Algorithmica, 2002, 32(4): 554-561.

[8]Wang L, Li Z. An Approximation Algorithm for a Bottleneck k-Steiner Tree Problem in the Euclidean Plane[J]. Information Processing Letters, 2002, 81(3): 151-156.

[9]Du D-Z, Wang L, Xu B. The Euclidean Bottleneck Steiner Tree and Steiner Tree with Minimum Number of Steiner Points[J]. Lecture Notes in Computer Science, 2001, 2108: 509-518.

[10]Li Z, Zhu D, Ma S. Approximation Algorithm for Bottleneck Steiner Tree Problem in the Euclidean Plane[J]. Journal of Computer Science and Technology, 2004, 19(6): 791-794.

[11]Bae S, Lee C, Choi S. On Exact Solutions to the Euclidean Bottleneck Steiner Tree Problem[J]. Information Processing Letters, 2010, 110(16): 672-678.

[12]Li M, Ma B, Wang L. On the Closest String and Substring Problems[J]. Journal of the ACM (JACM), 2002, 49(2): 157-171.

[13]Sarrafzadeh M, Wong C K. Bottleneck Steiner Trees in the Plane[J]. IEEE Transactions on Computers, 1992, 41(3): 370-374.

[14]Lin G, Xue G. Steiner Tree Problem with Minimal Number of Steiner Points and Bounded Edge-length[J]. Information Processing Letters, 1999, 69(2): 53-57.

[15]Cardei I, Cardei M, Wang L, et al. Optimal relay location for resource-limited energy-efficient wireless communication[J]. Journal of Global Optimization, 2006, 36(3): 391-399.

[16]Li Z, Xiao W. Nearly Optimal Solution for Restricted Euclidean Bottleneck Steiner Tree Problem[J]. Journal of Networks, 2014, 9(4): 1000-1004.

[17]Li Z, Xiao W. Determining Sensor Locations in wireless sensor Networks[J]. International Journal of Distributed Sensor Networks, 2015, 2015:1-6.

[18]Zhou H, Shenoy N, Nicholls W. Efficient Minimum Spanning Tree Construction without Delaunay Triangulation[J]. Information Processing Letters, 2002, 81(5): 271-276.

[19]Guibas L, Stolfi J. On Computing all North-east Nearest Neighbors in the L1 Metric[J]. Information Processing Letters, 1983, 17(4): 219-223.

[20]Coemen T H, Leiserson C, Rivest R, et al. Introduction to Algorithms[M].3rd Edition. Boston: MIT Press and McGraw-Hill, 2009.

2016-03-22

李子茂(1974-),男, 副教授, 博士, 研究方向: 算法设计与分析、计算复杂性, E-mail：3030207@mail.scuec.edu.cn

国家自然科学基金资助项目(61103248；61379059)

TP312

A

1672-4321(2016)03-0097-05

网格空间瓶颈斯坦纳树问题快速近似

李子茂，李晓丹

( 中南民族大学 计算机科学学院，武汉430074)

指出了瓶颈斯坦纳树问题要求寻找一棵用至多k个斯坦纳点将n个点连接起来使得此斯坦纳树之最长边最短的斯坦纳树,该问题在VLSI、无线通讯网络和生命演化树重建等领域都有应用.Du和Wang证明网格空间瓶颈斯坦纳树问题是NP-Hard，不存在近似性能比低于2的多项式时间解决方案，并且提出一个近似性能比为2的多项式时间近似算法，算法的实际时间复杂度为O(nlog2n+kn+k2).通过引入二叉堆和斐波那契堆使算法的时间复杂度分别改进到了O(nlog2n+klog2n)和摊还时间O(nlog2n+klog2n).该改进可直接应用于欧几里得平面的瓶颈斯坦纳树2-近似算法.

瓶颈斯坦纳树；近似算法；性能比；无线通讯网络